组织“具象”思维，实现意义学习目标

高文

【摘 要】“景由心生”，对客观现实进行取舍改造，保留一定形态，却又明显有人为的因素，以此触发学生心灵深处的形象世界，使学生的认识从感性进入抽象，从而在具象思维中逐渐获得某种思想方法和思维模式，最终形成超越现实的教学效果。因此，教师必须站在小学生的视角组织教学具象，构建具象思维场景，开展具象思维活动，努力促进高质量的同化，最终实现新意义的合理建构。

【关键词】教学具象；具象思维；意义学习

教学具象，是指教学过程中呈现在师生大脑中的形象。它是对学生已积累的若干表象，进行加工而形成的规范的形象。“具象”思维是学生在教师的指导下，对教学具象开展观察、分析、推理的思维活动。从心理学层面理解，小学生的学习大多从教学具象开始，通过具象的逐步展现激发小学生的探究欲望从而启发思维。

教师通过创设与自然对象较为相似的关联场景，让学生置身于有意义的学习环境，可以多维度地为学生“创造学习经历”，开展领悟个体学习经验、体验同化过程、实现意义整合的经验提炼活动，实现促进学习、改善学习、提升学习的目的。

一、构建具象思维场景

美国心理学家梅耶认为，意义学习重在帮助学生领悟自身的经验，充分尊重人类有限的认知容量，积极进行认知加工——主动选择信息、组织信息和整合信息。在意义学习过程中，具象思维起着关键作用，既要切合小学生的心理特点、认知结构，也要循序渐进。选取教学具象，承载教学内容，构建合适的教学场景，引导学生进行分析、抉择、取舍、凝练，最终发现知识的本质，整个学习妙在“从具体到抽象” 的过程。

（一）科学选择教学具象

教学具象的选择必须科学，必须选择与教学目标的实现密切相关的、高度体现阶段性教学目标的形象。教学具象具有以下特征：第一，背景上相似；第二，与已学知识关联度较高；第三，承载的内容深度契合学生认知结构。通过具象的逐步呈现，启发学生开展连续的观察思考，发现新旧知识联系点，衔接旧知，逐渐理解建构新知，促进学生“经历”意义学习的过程。

例如，教学认识轴对称图形。建立概念的过程，是感知和认识概念，抽象、概括其本质属性的过程。如何让学生获得充分、深切的感知，深刻理解轴对称的概念，是教学面对的现实问题，因此，教师选择了生活中有轴对称特征的几个基本形象，出示经过加工规范后的形象，展开教学。

师：我们把数学书第107页的3个图形沿轮廓剪下来，可以得到蝴蝶、天坛和飞机这3个规范图形，把这3个图形分别对折，看一看，比一比，想一想，你能发现什么？和同桌说一说。

反馈：谁愿意把你的发现说给全班同学听？

指名3个学生分别演示，对折3个图形：通过观察，你看到了什么？

生：每个图形的两边都重叠在一起。

點拨：两边的形状一样吗？大小呢？

引导学生抽象、概括：两边的形状和大小完全相同，我们就说这样的图形是对称的。

引导再提升：像这样沿折痕对折后两边能完全重合的图形，是轴对称图形。

学生通过观察操作这几个教学具象的例子，经历理解、获取、发现“轴对称”本质属性的活动过程，获得充分、深切的感知。

（二）教学具象适时变通

具象思维以物为媒，以物象操作激发学生的思维意识，对反映在意识中的物象进行有目的操作思考活动。合理的具象变式可以激发学生对变式线索的反思，提取已经编码和存储在头脑中的知识和表象，进行比较、诊断，排除定势对概念本质的干扰，清晰地发现其内在的结构，促使学生对数学概念的认识由粗疏走向“精致”。

例如，教学“认识分数”片段，在学生经历了把4个桃、2个桃、1个桃平均分成2份的连续教学场景后，教师适时变化。

师：如果现在有7个桃，平均分成2份，每份能用[12]表示吗？（同桌讨论……）

生：7是单数，不好分，而且1猴分3个，另1猴分4个。

生：可以把1个桃平均分成2份。

生：可先把6个桃平均分成2份，再把剩下的1个桃平均分成2份。

师：如果现在有100个桃平均分成2份，每份是多少？如果现在有1篮桃呢？

生：都可以用[12]来表示，多1个都平均分成2份。

小结：无论桃有多少个，把这些桃平均分成2份，每份都可以用[12]表示。

学生在变式中探究，对前面的浅显认识作理性思考，修正已有的学习表象，清晰获得有关[12]的认识。

二、开展具象思维活动

具象既是教学过程中具体的基本形象，也是活跃在师生头脑中的形象，即心灵的具象，是学习主体与学习对象的遭遇之处。如何通过场景设置，引起意识冲突，形成新认识？需要学习者在对教学具象的探究过程中，发现能进行同化的点，通过不断同化，不断改变和重组，使一个个新发现成为后续学习的固着点，才能使新知识被逐渐理解并保持下来，新知识的意义才会转化为学生的实际心理意义，学生原有的认知结构才会扩展。

（一）以形为本创造形象

人的思维有两个方面：第一是具象思维，第二是抽象思维。我们在教学中不能忽视具象思维，它可以用合适的教学具象来清理和重构我们抽象的思维系统，使我们在思考和沟通时更接近我们想学的内容，具有更快速、更直观的有效性。当学生在探索思考时，不知道怎么用语言描述时，教师及时把分散的生活对象提炼成几何具象，为学生搭一个阶梯，让学生借助具象观察、分析、探究、验证、深入思考，有利于发现知识的本质，促进同化，也有利于学生进行直观检验，形成新的技能、方法及模型，最终理解并掌握新知识。

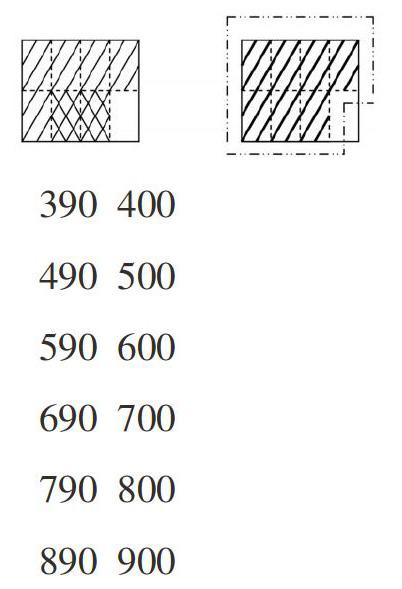
例如，学生刚学习“分数加法”时， 对于分数加法的算理理解不透彻，教师及时补充一题，计算5个[18]加2个[18]。

提问：如果没有巧克力这个实物，怎样才能更清楚地看出合起来一共吃了这块巧克力的几分之几呢？

生：我们就画一个长方形，把这个长方形平均分成8份，其中的5份涂上红色，2份涂上绿色，就可看出一共是它的几分之几。

生：也可以画一个圆……

师演示提炼成的几何具象。

让学生借助图形看到5个[18]加2个[18]是7个[18]，就是[78]。通过这两个分数由分到合的动态演示过程，直观验证了分数加法就是把两个数合并为一个数的过程，它是整数加法意义的扩展，分数加法与整数加法的计算法则产生了横向和纵向的跨连接，从而发现分数相加计算的通則，实现了融会贯通。

（二）以思助化活用具象

思维可以具象化为行为、文字、声音、形象，经过信息传递运动被还原成学生头脑里的意象。如果课堂里有关概念的心理表征中的联系十分脆弱，这时的同化就很浅显，教师要着眼于“最近发展区”，采取恰当的教学策略，引导学生循序渐进地对应拓展知与象的容量，根据边际效益的观点，只要我们不断地强化具象思维，通过占有很多具体的象来清理和重构教学语言，学生就能逐渐地知道“说什么”，以思助化，形成思维的“张力”。

例如，教学“认识千以内的数”时，整个教学过程随着对应数与珠的知识容量的逐渐扩展，前后知识间的联系顺畅，学生的具象思维越来越活跃。

师：一十一十地数，应在哪一位上拨珠？390添1个十是多少？

生：400。

师：怎么拨珠的？为什么向百位进1？

生：十位满10，向百位进1。

生继续一十一十地拨珠数，师演示板书：

引导学生观察比较：后面这些数多了1个百，是哪里来的？

生（齐）：十位满10，向百位进了1。

师：990添1个十是多少？

生：1000。

师：是吗？动手拨拨看。

生说师演示：990添上10是1000的连续拨珠过程。（板书：990 1000）

然后师生一个一个地拨珠数，从399数到400。

师：你又有什么发现，多的1个百哪里来的？

生：个位满10向十位进1，十位满10向百位进1。

师（拨珠）：999添上1是多少？

生边演示师边板书：九百九十九添上一是一千。

教师引导学生借助计数器读、写千以内的数，从具象到抽象不断地经历数数的详细过程，体现出数和珠的一一对应性，理解每两个相邻计数单位之间都是十进制的关系，学会了数千以内的数，了解数的组成，亲身经历数的发现、理解、掌握、运用的过程。

三、实现意义学习目标

教学具象是对自然对象适当变形和合理规范，或将不同自然对象进行适度的重合提炼，从而达到教学的和谐状态。具象思维是科学的物象思维，学生从这些可辨识的具象出发，就能找到理解抽象知识的线索，进一步开展学习活动，实现信息的加工、整合，思维不断扩大和增强，从发散至凝聚，产生新的观点，更新信息，新的意义就生了根。

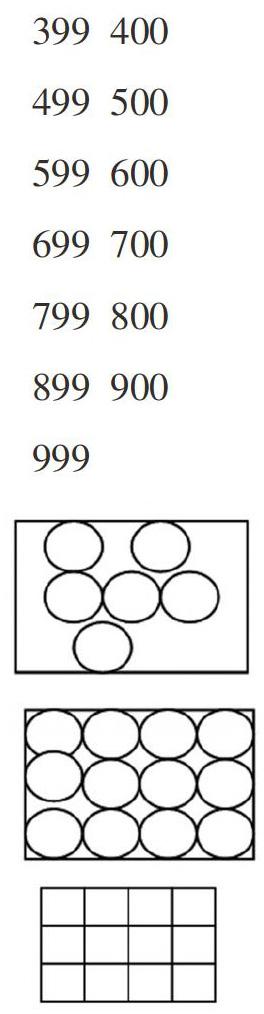
例如，教学解决问题的策略（面积）的教学片段：

师出示长方形，用地砖铺出地面面积。

要求：（1）同桌合作；（2）先用两种地砖分别试一试，再选择一种合适的铺一铺；（3）看一看你铺出的面积在哪里。

生：我铺了，没有铺完。

生：你没有铺满整个长方形。

生：我铺满了，是这样铺的。

生：你铺的是面积吗？你缺少了一点点，就不是面积。

师（及时肯定）：面积必须把整个地面铺满。

然后学生准备长方形的地砖，再次铺地面。

师：现在有没有铺满？

教师引导学生抓住关键，通过模拟铺地砖的场景，培养学生有序地动手铺、有序地思考的习惯，信息不断更新，清晰的面积概念逐渐生根，获得了基本的数学思想方法。

赫斯特指出：知识的不同形式是人类理解世界与人类自己的认知框架；理解的过程就是意义被赋予的过程。“景由心生”，对客观现实进行取舍改造，保留一定形态，却又明显有人为的因素，以此触发学生心灵深处的形象世界，使学生的认识从感性进入抽象，从而在具象思维中逐渐获得某种思想方法和思维模式，最终形成超越现实的教学效果。因此，教师必须站在小学生的视角组织教学具象，构建具象思维场景，开展具象思维，努力促进高质量的同化，帮助尚未掌握方法的学生掌握方法，帮助初步掌握方法的学生掌握得更牢固，最终实现新意义的合理建构。

（江苏扬州江都区仙女镇中心小学教育集团花园校区 225200）