改进的MEMS陀螺随机噪声自适应滤波算法*
2018-09-27唐晓红赵鲁阳李鲁明
唐晓红, 赵鲁阳, 李鲁明,3, 何 为, 王 沛
(1.中国科学院 上海微系统与信息技术研究所 宽带无线技术实验室,上海 200050;2.上海师范大学 信息与机电工程学院,上海 200234;3.中国科学院大学,北京 100049)
0 引 言
微机电系统(micro-electro-mechanical system,MEMS)陀螺仪[1,2]是惯性导航系统中测量载体角速率的关键性器件,性能主要是受到常值误差及随机误差的影响,抑制随机误差,通常需要建模及滤波等方式来进行补偿。本文采用Allan方差分析方法对MEMS陀螺仪输出数据进行随机误差辨识,建立自回归滑动平均(auto-regressive moving average,ARMA)数学模型。针对模型中的有色噪声,无法采用状态扩充法进行白化[3],本文提出将其引入系统状态方程中,作为方程的控制项,对解耦自适应Kalman滤波算法进行改进,实现对MEMS陀螺仪随机噪声的滤波补偿。
1 Allan方差分析法
1.1 Allan方差的基本原理
对于时间序列{xt},其样本数据的总长度为N,采样时间为τ0,把样本数据平均分为K组,每组样本数据的长度为M<(N-1)/2。将τ=mτ0,(m=1,2,…,M)定义为相关时间,每一个相关时间下,每一组样本数据的平均值为xj(M),则Allan方差计算方法为
(1)
1.2 Allan方差的应用
1)随机误差辨识
MEMS陀螺仪随机噪声主要包括:量化噪声Q(μrad)、角度随机游走N((°)/h1/2)、零偏不稳定性B((°)/h)、角速率随机游走K((°)/h3/2)及速率斜坡R((°)/h2)[4]。各随机误差项在Allan方差曲线中,直线斜率不同。
假设各项随机噪声相互独立,根据Allan方差σ(τ)与MEMS陀螺仪随机噪声的对应关系,则有
(2)
将式(3)中的多项式系数采用最小二乘法进行拟合有
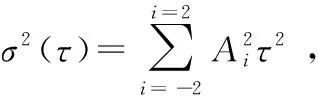
(3)
2)量测噪声方差估计
Allan方差滤波器可直接滤除系统噪声中部分低频噪声,量测噪声的方差近似等于宽频噪声的Allan方差[6]。相关时间为采样时间τ0时,Allan方差为
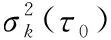
(4)
则量测噪声方差为
(5)
式中k=2,3,…;初值1可任意选取。
2 数据采集、预处理与检验
2.1 数据采集
本实验所测试的MEMS陀螺仪为MPU6050,使用STM32F030CCT6通过I2C总线读取MPU6050的数据。实验数据通过串口模块、蓝牙模块进行接收、发送,由MATLAB读取并记录串口数据。在AeroSmith高精度单轴转台上,安装MEMS陀螺仪,如图1所示,静止预热20 min。设定采间隔时间为10 ms,以100 Hz的采样频率连续采集90 min数据。

图1 MEMS陀螺仪转台测试
2.2 数据预处理
在建立MEMS陀螺仪样本数据的时间序列模型前,对MEMS陀螺仪原始数据进行预处理以确保样本数据的零均值、平稳性以及正态性,通过提取样本均值的方式进行消除常值误差。由于周围环境以及MEMS陀螺仪自身因素的干扰,会产生一定的趋势性变化,可采用多项式拟合法[7]提取趋势项。依据PauTa准则[8],若超过3倍测量值的标准偏差,则认为该数据是异常值,从测量数据中剔除。本文采用样本数据均值代替异常值的方式来剔除异常值,预处理前后MEMS陀螺仪的角速度数据如图2所示。
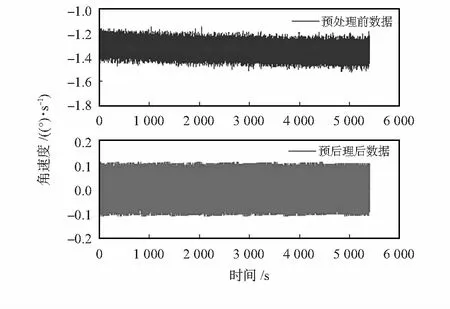
图2 MEMS陀螺仪预处理前后数据
2.3 平稳性及正态性检验
1)平稳性检验
预处理后的陀螺仪数据采用轮次检验法[9]进行平稳性检验。样本数据的游程总数为r=16,查游程检验分布表,在显著水平α=0.05下,其接收域为6≤r≤16。故样本数据为平稳的随机信号。
2)正态性检验
将样本数据分为K组等间隔区间,统计其在各组区间的个数。MEMS陀螺仪输出角速度数据的频数直方图基本服从正态分布。
3 模型建立
对于平稳时间序列样本{xt},t=1,2,…,N,其ARMA(p,q)为
(6)
式中N为数据样本长度;εt~WN(0,σ2);p,q为模型阶数。通常,MEMS陀螺仪误差建模不会超过3阶,且p≥q。则,可建立模型ARMA(1,1),ARMA(2,1),ARMA(2,2)。
赤池信息(Akaike information criterion,AIC)准则为
(7)
则3种ARMA模型的AIC值分别为-6.623 309,-6.623 351,-6.623 347,且ARMA(2,1)模型的AIC值最小,可作为MEMS陀螺仪的随机误差模型。
本文采用自回归逼近法[10]进行ARMA(2,1)模型的参数估计:
1)建立高阶的AR(6)模型,逼近ARMA(2,1)模型
xt=0.022 7xt-1+0.009 1xt-2+0.004 9xt-3+
0.007 3xt-4+0.007 7xt-5+0.008xt-6+εt
(8)
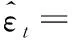
0.007 3xt-4-0.007 7xt-5-0.008xt-6
(9)
3)建立的ARMA(2,1)模型为
xt=0.917 1xt-1-0.011 2xt-2+εt-0.894 5εt-1,
εt~WN(0,0.001 33)
(10)
4 Kalman滤波补偿
设A为状态转移矩阵,B为系统噪声矩阵,H为量测矩阵,Wk和Vk分别为系统过程噪声和量测噪声,根据所建的ARMA(2,1)模型,滤波器的参数设置如下
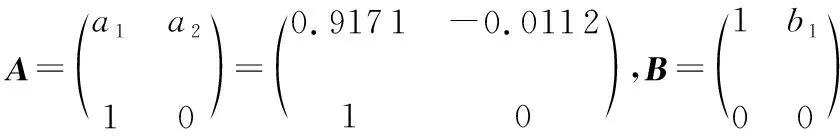
(11)
基于ARMA模型的系统状态方程亦可写为
Xk=A·Xk-1+Sk,Sk=[εk+b1·εk-10]T
(12)
可知系统噪声Sk为有色噪声。通常采用状态扩充法,将系统有色噪声扩充到状态量中,进行白化有色噪声。而该方法对有色噪声进行白化的成形滤波器,其固定形式为
Sk+Π·Sk-1=εk
(13)
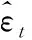
(14)
(15)
根据ARMA模型可得系统过程协方差Q,本文将固定Q阵,只对量测噪声协方差R阵进行自适应,则改进的解耦自适应Kalman滤波方程为
(16)
5 实验与结果分析
为了验证本文所提的改进的解耦自适应Kalman滤波算法的正确性与有效性,根据建立的ARMA(2,1)模型及滤波方程,分别对Kalman滤波算法,解耦自适应Kalman滤波算法[11,12]和本文算法进行仿真,如图3所示。
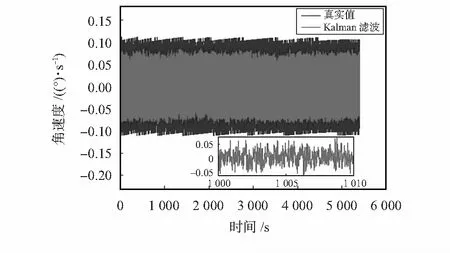
(a) 标准Kalman滤波前后结果
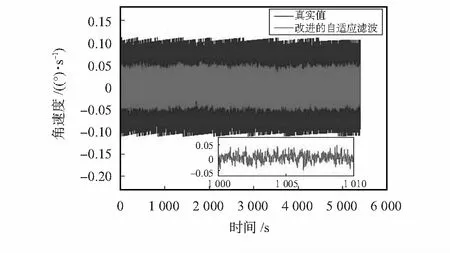
(c) 改进的解耦自适应Kalman滤波前后结果图3 三种算法滤波前后仿真结果
可见本文所提改进算法、解耦自适应Kalman滤波的效果均好于标准Kalman滤波。MEMS陀螺仪滤波前后数据的统计特性均方差:表明3种算法滤波后的噪声均方差为:Kalmax滤波算法为0.000 637,解耦Kalman滤波算法为0.000 291,本文算法为0.000 198,相比滤波前均方差(0.001 33)均减小了一个数量级。与滤波前相比,Kalman滤波后的噪声均方差减小52.1 %,解耦自适应Kalman滤波后的噪声均方差减小78.1 %,改进的解耦自适应Kalman滤波的噪声均方差减小85.1 %。说明本文所提改进算法较其他2种Kalman滤波具有更好的滤波效果。
MEMS陀螺仪的短期误差表现为角度随机游走,长期误差表现为角速率随机游走[11]。为了更进一步验证本文所提改进算法的正确性与有效性,对MEMS陀螺仪滤波前后的随机误差项进行对比分析,如表1所示。
根据表1,经改进的解耦自适应Kalman滤波算法滤波后,2种误差项皆可有效减小41.9 %。相较于Kalman滤波算法、解耦自适应Kalman滤波算法,本文所提改进算法的随机误差项分别减小30.5 %,10.1 %。表明本文所提改进算法可更好地提高MEMS陀螺仪的输出精度,减小随机噪声对MEMS陀螺仪性能的影响。
6 结 论
本文对解耦自适应Kalman滤波算法改进,对改进算法、Kalman滤波算法、解耦自适应Kalman滤波算法进行仿真,从数据的统计特性均方差、MEMS陀螺仪的随机误差项,对滤波前后的数据进行对比分析。实验结果表明,本文所改进的算法可有效减小MEMS陀螺仪随机误差,其滤波效果优于Kalman滤波算法、解耦自适应Kalman滤波算法,对提高MEMS陀螺仪的精度具有一定的工程实用性。
