带全局判据的改进量子粒子群优化算法

徐珊珊, 金玉华, 张庆兵

(中国航天科工防御技术研究院, 北京 100854)

0 引 言

工程优化问题通常具有优化参数较多、非线性较强和同时存在多个局部最优解的特点。因此,优化算法需要在较短时间内,促使多个优化参数同时收敛到全局最优位置,以增大得到全局最优解的概率。近年来,研究人员已针对该问题开展了大量研究。

粒子群优化(particle swarm optimization,PSO)算法是由Eberhart和Kennedy等人于1995年提出的基于种群并行全局优化算法。其源于对鸟群群体协作的捕食行为模拟,通过种群间个体的协作,引导整个群体向可能解的方向移动[1-3]。与其他全局优化算法相比,PSO算法具有程序简单,多维并行优化,优化速度较快的优点,已获得广泛的应用[4-6]。但其也具有一定局限,比如容易局部收敛、收敛速度较慢等。文献[7-8]等综合前人工作[9-10],将粒子速度或位置小概率随机变异与自适应逃逸策略相结合,提出了全局搜索性能较优的改进PSO算法,并将其运用在气动力计算、高超声速飞行器设计等方面。但这些算法收敛速度较慢,导致迭代步数较多(文献[7]为2 000步),计算成本大大增加。

为增大粒子搜索范围,文献[11]从量子力学的角度出发,认为种群中的粒子具有量子行为,在某种吸引势能场的作用下会以一定的概率密度出现在设计空间的任意一点,因此提出了优化时间仅为PSO算法1/3的量子PSO(quantum-behaved particle swarm optimization,QPSO)算法。QPSO算法具有鲁棒性强,计算速度快的优势,已运用在2D火焰温度测量[12]、超光谱图像端元提取[13-14]、正电子发射断层显像建模[15]、脑电图信号分类[16]、经济调度[17]等领域,并发展到多目标优化[18-19]和动态优化[20-23]方向。但由于QPSO算法在粒子进化过程中,惯性权值β随进化代数增加而线性减少,易出现早熟收敛,且易导致算法收敛过慢。文献[24]等采用适应度加权重组算子改进了QPSO算法;文献[25]等引入服从高斯概率分布的局部因子,以增大粒子全局性;文献[26]等发展了根据粒子适应度分布情况进行粒子位置搜索范围变化的自适应QPSO方法;文献[27]结合云模型,发展了自适应云QPSO改进方法;文献[28]将自适应云QPSO算法与图像识别技术结合,提高了图像识别准确率;文献[29]采用改进的混合蛙跳算法进行局部搜索,将参数自适应和精英学习策略引入优化状态评估;文献[30]利用布洛赫球体上一个轴的旋转来更新粒子,提出了布洛赫球面改进(bloch sphere-based QPSO,BQPSO)算法;文献[31]提出了一种基于列维飞行的量子粒子群优化算法;文献[32]采用分层协同进化的方法改进QPSO算法, 并应用于新生儿脑组织的研究;文献[33]提出了惯性权重自适应调整的QPSO(dynamically changing weight’s QPSO,DCWQPSO)算法,并研究了单参数优化问题算法收敛的参数设置。但当优化参数增多时,以上改进算法极易收敛到局部最优解,对于较为复杂的测试函数,20和30维粒子的优化结果仍有较大提升空间[24-31],将无法符合实际工程问题对多参数优化的需求。

不仅如此,由于粒子具有量子行为,QPSO算法具有很强的随机性。对于未知问题,工程人员无法判定优化结果是否为全局最优解。现有办法仅依靠优化算法对优化算法Benchmark测试函数的优化能力,进行粗略判断,或者采用“多次独立优化,选取最优解”的方法。显然,采用这些人工筛选的方法不仅将消耗大量计算时间,全局最优解的判定还仍然无法准确得到。所以,针对工程应用,优化算法更需要在优化过程中自行判定优化结果的全局性,直接输出全局最优解。

因此,本文首先针对多参数优化问题的全局搜索能力,对DCWQPSO算法进行了粒子位置周期性变异及随进化速度和粒子聚集度变化的搜索范围变异,并依据Benchmark函数优化结果进行了参数讨论。然后,针对未知问题无法判定优化结果全局性的问题,本文建立了全局收敛判据。最后,针对乘波体最大升阻比的前缘线多参数优化问题,本文采用带全局判据的改进QPSO(improved QPSO with global criterion,GCIQPSO)算法进行了参数优化。结果证明,对于多参数优化问题,本文算法的全局搜索性能大大提高,全局判据实用性强,优化结果可靠。

1 DCWQPSO算法

QPSO算法引入δ势阱模型,通过求解薛定谔方程得到相关波函数Ψ(x,t),进而计算出粒子在设计空间内某一处的概率密度函数,最后由蒙特卡罗方法确定粒子的新位置。位置方程x(t)的第i维表达式为

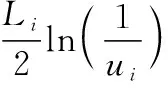
(1)

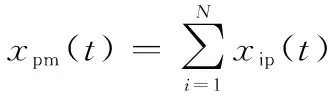
DCWQPSO算法把惯性权重β的表达式改进为与进化速度因子sd和粒子聚集度因子jd有关的自适应权重。其表达式为

β=f(sd,jd)=β0-sdβ1+jdβ2

(2)

2 带全局判据的改进QPSO算法

对于多维参数优化问题,粒子的搜索范围需要大大增加,才能保证各维粒子寻找到全局最优位置的概率增大,优化结果收敛于全局最优解的概率才能有所增加。因此,本文提出了带全局判据的改进QPSO算法(global criterion improved QPSO,GCIQPSO)算法,不仅提高粒子群搜索范围,增大得到全局最优解的概率,还对优化结果进行全局性判断,无需人工筛选,直接得到全局最优解。

2.1 改进DCWQPSO算法

由式(2)可知,β1代表进化速度快慢在惯性权重中的占比,β2表示粒子聚集度大小的占比,β的大小直接影响了粒子更新的范围。若优化陷于局部最优解,则粒子群的全局最优位置固定,sd=1,无论粒子聚集度jd大小如何,β只能在[0.5,0.7]范围内变化,产生的粒子搜索范围下降,较难寻找到全局最优解。不仅如此,从式(2)可以发现,一旦优化过程陷入局部最优状态,随着迭代步数的增加,粒子群将逐步靠近该局部最优位置,使得jd也不断趋于定值,β随之固定,新粒子寻找到全局最优解的概率进一步下降。由此可见,随着局部收敛的出现,DCWQPSO算法的粒子种群多样性将不断恶化,直至失效。

为增大粒子多样性,避免粒子群陷入局部最优,本文首先加入粒子位置周期性变异,每迭代T步变异一次，即

xi(t)=xi(t)[1+(0.5-randi(0,1))δ]

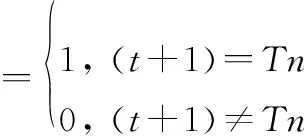
为得到较为通用的结论,本文选择CEC2005函数中结果较不理想[7,11,24-33]的测试函数及其复合形式,并添加两种复杂函数[30]组成8个优化测试函数(函数形式见表1),并采用30个30维粒子[7,30]组成优化粒子群(f6(x)函数取32维粒子)。由于QPSO算法随机性较大,为体现优化结果的平均性,本文采用100次独立优化的结果,具体数据如表2所示。

表1 8个优化测试函数

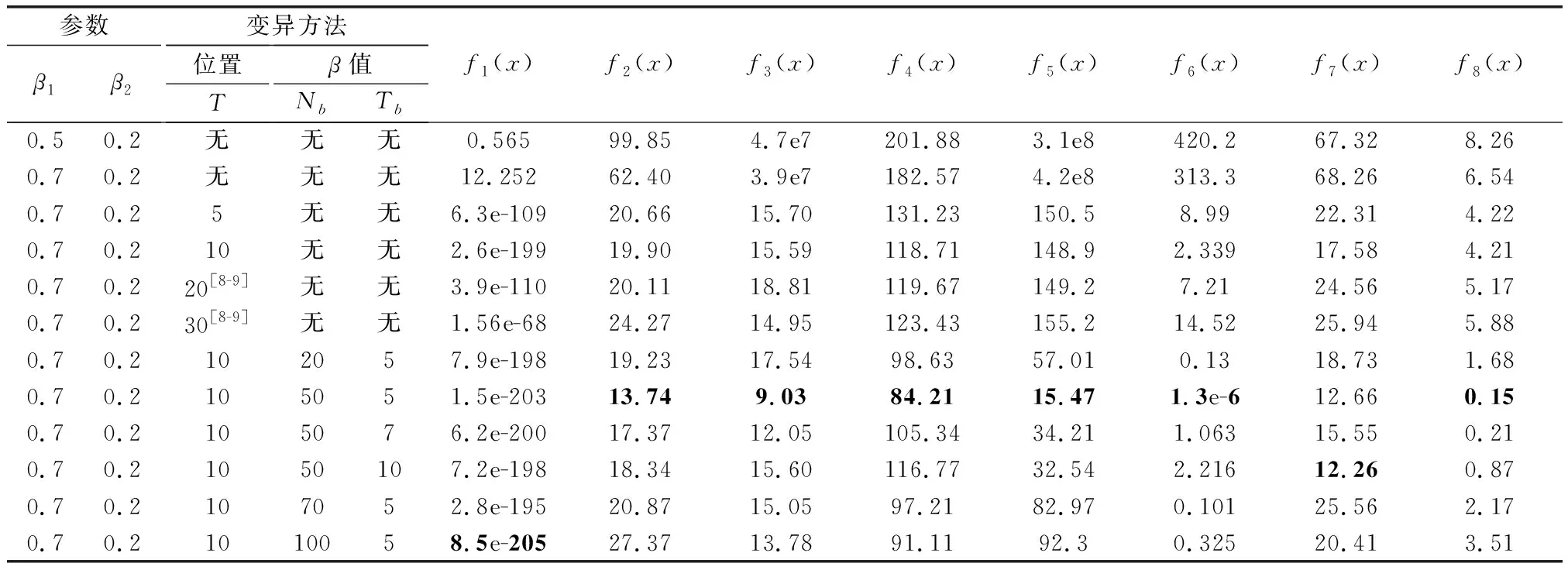
表2 不同函数的30维30个粒子的粒子群100次独立优化平均值

从DCWQPSO优化结果可见,优化参数增多后,除f1(x)和f5(x)外,其他函数的β1=0.7优化结果更稳定,明显优于β1=0.5,与文献[32]的单参数优化研究结论有所不同。增加位置周期性变异后,8种函数的粒子群全局搜索能力均有提高:f1(x)、f3(x)、f5(x)、f6(x)函数的优化结果提高幅度最大;由于f8(x)函数本身精度较好,改进后提升空间最小;f2(x)和f7(x)(f2(x)函数的非连续型)次之。而随着变异周期从30减小至10,8种函数的优化结果精确度均有提升,但若进一步减小(T=5),粒子的继承性无法体现,不利于全局搜索能力的提升。对f1(x)、f2(x)、f4(x)～f8(x)函数而言,T=10优化结果最佳;对f3(x)函数而言,T=30周期的平均优化值最佳,T=10的优化结果次之。综合而言,本文选择T=10为位置变异周期。

从表2可发现,粒子位置周期变异能有效增加多样性,单峰二次函数f1(x)的100次独立优化平均值有较大提升,优化结果精度较高。但其余7个函数优化结果仍有一定提升空间。

由第1节可知,粒子搜索范围主要由势阱的特征长度L决定,扩大β的取值范围最为关键。本文研究了位置变异后全局收敛提升较小的f2(x)函数优化结果的β值变化趋势(见图1)。

图1 不同优化结果的βFig.1 β curve with various optimization results

从图1可见,局部收敛越明显,β值越容易集中于一点,极大地影响了粒子群的搜索范围。因此,本文在粒子位置周期变异的基础上,增加了β值变异。具体方法为

βi(t)=βi(t)[1+(0.5-randi(0,1))δ]

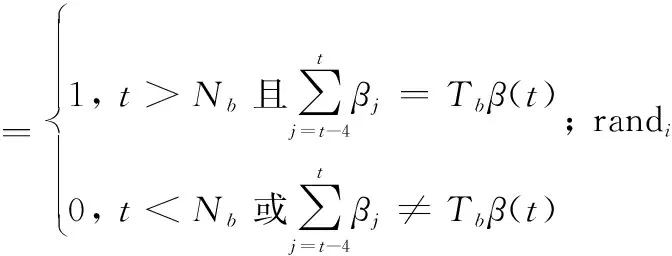
粒子位置变异直接改变粒子位置,具有一定随机性,但往往无法有效增大全局搜索范围。而β变异直接对粒子的搜索能力进行判断和变异,以扩大搜索范围。因此,在粒子达到一定搜索能力后,β变异启动较为有效,Nb不宜过小,但过大的Nb又无法有效提升已陷入局部最优的粒子全局搜索能力。而β在Tb步内是否保持不变代表了粒子全局搜索范围是否持续增加,β变异周期Tb需不大于粒子位置变异周期T,但过小的Tb会使粒子无法有效继承前粒子的优化成果,自适应惯性权重优势无法体现。

为研究Nb和Tb的设置,本文同样采用8个测试函数进行30维30个粒子的100次独立优化,优化结果列于表2,每个函数的最佳值均用黑体标出。从结果可见,双重优化降低了f2(x)～f8(x)函数优化结果与全局最优解的距离,f1(x)函数的精确度仍满足要求。当参数Nb=50和Tb=5时,除f1(x)和f7(x)外,β值变异最有效。

综上,粒子位置周期变异与β变异结合的方法,能有效增大粒子群全局搜索能力,多维函数优化结果收敛于全局最优解的概率大为增加,且参数选择T=10、Nb=50和Tb=5效果最好。

2.2 全局收敛判据

优化算法的全局搜索能力越强,优化结果收敛于全局最优解的概率越大,而每一迭代步的粒子分布范围大小则代表了全局搜索能力的强弱,不仅如此,其也可以表征粒子位置周期变异能否扩大粒子的全局搜索能力。由第1节定义可知,粒子聚集度jd表示当前迭代步下,各粒子历史最优解和当前全局最优解的比值。其物理含义包括:①jd值不断变化直观体现了粒子的全局搜索能力是否持续扩大。随着迭代步数增加,若其值不断变化,则表明新粒子搜索到了更优解;若保持不变,则表示新粒子无法得到更优解;②jd值大小表示迭代过程的收敛程度。其值在0～1范围内变化,数值越大表示各维粒子局部最优解的均值越趋近于全局最优解,迭代过程越趋于收敛;③jd值的变化剧烈程度直接体现了整个寻优过程粒子群的多样性大小,若均值和方差均较低,则表示整个迭代过程粒子群无明显收敛,且离散度较大,一直保持寻优状态,全局搜索能力高,变异方法较为有效。所以,本文研究了jd的变化剧烈程度,并以此作为优化结果是否收敛到全局最优解的依据。

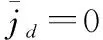
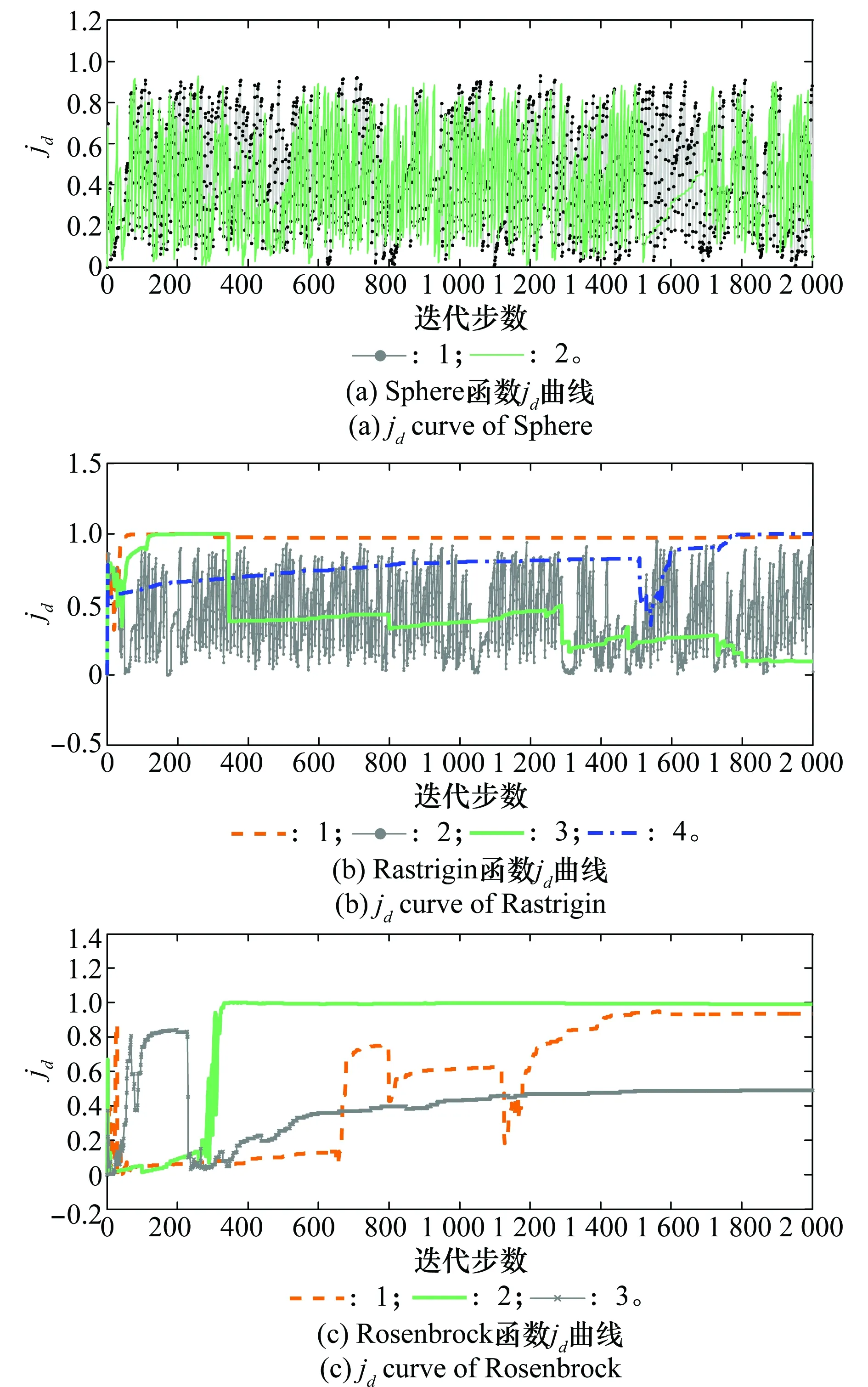
图2 不同函数和优化结果下,jd的变化曲线Fig.2 jd Curve of different functions with various optimization results

由图2可见,其优化结果最趋近于全局最优解的算例,jd曲线变化最为剧烈(如Sphere函数曲线1和2,Rastrigin函数曲线2,Rosenbrock函数曲线3);优化结果越偏离全局

最优解时,jd曲线变化越平缓(如Rastrigin函数曲线1和4,Rosenbrock函数曲线2);且优化结果的好坏与jd值最终的大小无关,仅与其均值和方差有关,jd值变化越剧烈,均值和方差越小。统计100 000次独立优化结果发现,当jd均值小于0.5,且标准差小于0.3时,2 000迭代步的优化结果99.8%为全局最优。

鉴于实际优化问题的复杂程度带来了较大的计算成本,迭代步数应尽量降低,本文选用200迭代步,再次进行了100 000次独立优化。结果显示,当jd均值小于0.5,且标准差小于0.3时,优化结果99.1%为全局最优。

因此,本文建立了针对优化参数大于5的多参数优化全局判据。其分为两个部分:①优化迭代中,粒子聚集度jd变化越剧烈,粒子的全局搜索能力越强,若其连续10步(粒子位置变异周期为10步,β变异周期为5步)均保持不变,说明双重变异对扩大全局搜索能力无效,则跳出此次优化,重新初始化种群,并将此次全局最优粒子作为其中一个初始粒子;②迭代结束时,若优化过程没有中断,迭代步数达到最大迭代值,则判断粒子聚集度jd是否满足“均值小于0.5且标准差小于0.3”的条件。若以上两个条件均满足,则存储优化结果,本次优化结束;若不满足,将本次全局最优粒子作为一个初始粒子,重新开始优化,直至满足条件(即可筛选局部最优解,也可保留不满足条件的全局最优解)。

某些低维参数优化问题较易收敛,导致jd值不变或其均值偏大,则储存每次全局优化结果。若5次均跳出且迭代结果不变,表示优化结果为全局最优解。对于未知问题,需独立优化3次,选取最优值。

2.3 GCIQPSO算法

GCIQPSO算法采用β值和粒子位置双重变异,jd变化剧烈程度、均值及标准差作为全局判据,每次独立迭代满足迭代步要求后,判断优化结果是否符合全局判据条件,若不符合重新初始化优化程序。

为验证全局判据的通用性,本文对8个测试函数,进行了30次独立优化,不同优化算法的结果如表3所示。

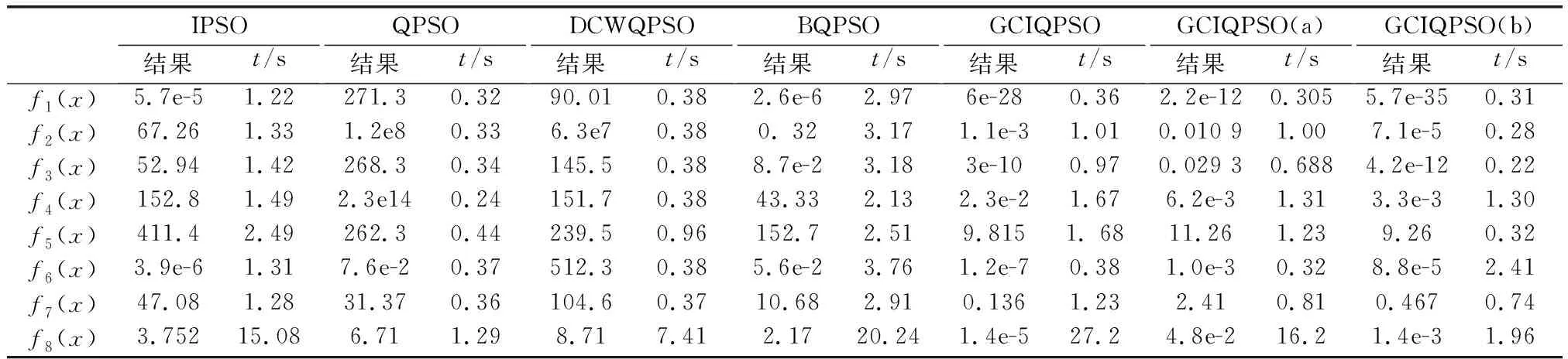
表3 测试函数的不同优化算法结果

由表3可见,与2 000步[7,30]优化结果相比,缩短迭代步数后,改进PSO[7](improved particle swarm optimization,IPSO)算法和BQPSO[30]全局搜索性能大为降低;而计算时间较短的QPSO和DCWQPSO算法,由于随机性较大,导致优化结果极不稳定,平均值偏离全局最优解的程度也较大。不同测试函数下,本文全局判据依然有效,优化精度远好于前4种算法。相比其他函数,f5(x)出现局部最优点的概率较大,优化精度不佳。因此,本文以2 000步为迭代步数,重新进行了30次独立优化,均值为0.064,平均时间为7.48 s。

经过试验发现,本文全局判据同样适用于前3种算法。但全局判据仅作为判断优化结果全局性的依据,不会扩大算法搜索范围。是否可与BQPSO结合,仍需进一步研究。

表3的GCIQPSO(a)列显示了迭代步数降低为150步的结果。虽然测试函数优化均值精度有所下降,但误差均在3%以内。但若迭代步数进一步降低,则全局判据需进一步收紧。GCIQPSO(b)列为粒子维度=4的150步优化结果,可见对于低维优化问题,全局判据依然有效。

3 乘波体前缘线多参数优化

为验证GCIQPSO算法对工程问题的实用性,本文选用了乘波体外形优化作为算例,设计方法、设计参数和优化参数与文献[34-35]保持一致,即:采用锥导乘波体设计方法和面元法的气动力估算方法;设计参数采用来流马赫数为6,飞行高度H=30 km,激波角β=12°,截止平面设定为单位长度;优化参数选取(x5,y1,y2,y3,y4),前缘线采用5个点的3次拟合曲线,目标函数为升阻比最大,约束条件为容积率大于0.07小于0.12,若优化结果不满足约束条件,则返回非数值(not a nuber,NaN)。乘波体前缘线优化流程如图3所示。

图3 乘波体气动外形优化流程Fig.3 Flowchart of cone-derived waverider configuration optimization

为节省计算时间,本文选择迭代步为150步,为防止不确定因素干扰优化结果,独立迭代3次,取最大值。迭代结束时,粒子聚集度jd标准差为0.28,均值为0.42,最大升阻比为6.28,比文献34的最大升阻比增大了20%,且与多次200步遗传算法(文献[34]采用)最优值一致。

4 结 论

针对多参数(参数个数不少于5)优化问题极易收敛到局部最优点和优化结果无法判断是否为全局最优解的问题,本文提出了改进的量子粒子群优化算法。具体结论如下:

(1) 在DCWQPSO算法基础上,本文增加了β值和粒子位置的双重变异,大大增强了粒子的全局收敛能力。Benchmark测试函数的优化结果全局性明显提升;

(2) 以粒子聚集度jd作为判断粒子全局搜索能力的依据,依据粒子周期变化是否对扩大粒子搜索范围有效和迭代结束所有粒子的全局分散情况为标准,建立了优化结果全局性的判据,使得优化过程去除人工筛选环节,直接输出全局最优解。本文通过Benchmark函数的大量试验验证,相较于其他优化方法,迭代步骤为150步的GCIQPSO算法优化结果均为全局最优解,远好于其他3种算法,且平均优化时间均少于IPSO算法。由此可见,本文全局判据简单可行,优化结果全局性十分突出;

(3) 为进一步验证GCIQPSO算法的工程应用价值,本文对乘波体前缘线优化问题进行了计算。结果表明,GCIQPSO算法得到的优化结果较文献[34]有了明显提高,满足全局判据,与遗传算法的多次试验结果一致。由此可见,对于多维优化的实际工程问题,GCIQPSO算法的全局搜索能力较好,全局判据可行,优化结果真实可信;

综上所述,本文提出的GCIQPSO算法是对多参数优化全局性判断问题的补充;其具有收敛速度快、全局搜索能力强、全局判据简单可行、优化结果真实可靠的优点;在较短时间内得到较为可信的全局最优解。GCIQPSO算法的优化效率较高,优化结果精度较好,可削减大量重复优化时间,省略人工筛选环节,具有一定学术价值和较大工程应用价值,可进一步拓展实际运用范围。