四旋翼无人机系统PD-ADRC串级控制

张 勇, 陈增强, 张兴会, 孙明玮, 孙青林

(1. 南开大学计算机与控制工程学院, 天津 300350; 2. 天津中德应用技术大学计算机学院, 天津 300350)

0 引 言

四旋翼无人机是目前比较常见的一种多旋翼无人机,它主要由十字交叉的对称机体以及4个螺旋桨组成,无人机的升力是通过4个电机对4个螺旋桨的转速改变而得到的,从而实现四旋翼的3个位置和3个姿态的6自由度控制。四旋翼无人机因其优越的低空飞行能力而受到广泛应用,关于四旋翼无人机的控制系统设计问题也成为了近年来控制领域的一个研究热点,由于四旋翼模型具有非线性、强耦合和不确定性,以及四旋翼无人机实际飞行环境的复杂性,要求控制系统应有较强的抗干扰能力和鲁棒性。针对以上四旋翼无人机的控制问题,目前国内外相关的控制方法有比例-积分-微分(proportion-integral-differential,PID)控制[1]、滑模控制[2-6]、四元反馈控制[7]、Backstepping[8]、线性二次型调节器[9]、鲁棒控制[10]、自适应控制[11-13]等。

文献[14]在20世纪80年代提出一种新的控制策略自抗扰控制技术(active disturbance rejection control technique)。自抗扰控制最核心的技术就是把被控系统内部的不确定因素以及外部扰动都看成是未知总扰动,然后用扩张状态观测器(extended state observer,ESO)对总扰动进行估计并在控制器中给予补偿。自抗扰控制器具有控制精度高、响应速度快、鲁棒性强等优点,因此在许多的理论研究和工程实际中都得到了广泛的研究与应用。但是自抗扰控制器是非线性的,这就使得控制器的参数过多,参数难以整定,算法不易实现。因此文献[15]提出一种线性自抗扰控制器,其参数少,便于参数调节和算法实现。

本文针对四旋翼无人机非线性、多变量、强耦合和对扰动敏感等控制问题,设计了比例-微分(proportion-differential,PD)和自抗扰的串级控制系统,其中位置回路采用了经典的PD控制,姿态回路分别用非线性自抗扰控制器(active disturbance rejection controller,ADRC)和线性自抗扰控制器(linear active disturbance rejection controller,LADRC)进行设计,在不加干扰和加干扰两种环境下,分别对两种控制器进行仿真,并对两种控制器的位置控制结果、姿态控制结果以及控制量信号进行对比分析。结果表明,在针对四旋翼的控制问题上,LADRC的控制结果更符合工程实际的需求,具有更强的鲁棒性和抗干扰能力。

1 ADRC的基本原理

非线性ADRC由跟踪微分器(tracking differentiator,TD)、ESO、非线性状态误差反馈控制律(nonlinear state error feedback,NLSEF) 3部分组成。LADRC由TD、线性ESO(linear ESO,LESO)、线性状态误差反馈控制律(linear state error feedback,LSEF)3部分组成。

1.1 TD

安排TD的目的是给系统输入设计一个平滑的过渡过程,进而得到光滑的输入信号,以降低系统初始误差。

以二阶连续系统为例,TD算法为

(1)

式中,v为设定值;r为决定信号跟踪快慢的可调参数;h为滤波因子。fhan(·)函数为最速控制综合函数,具体算法为

(2)

1.2 ESO

ESO是指除了被控对象本身的状态,还要把对象内部的不确定性以及外部扰动作为未知总扰动,扩张成另一个新的状态。通过观测器将总扰动观测出来,并加到控制器中进行补偿,这样就能使原来的非线性控制系统变成线性的积分器串联控制系统。上述动态估计补偿总扰动的方法,就是自抗扰控制的核心技术。

连续形式的LESO算法为

(3)

为了将LESO的参数都能用ωo来进行表示,现将LESO的极点全部设置在-ωo处,表示为

sn+β1sn+1+…+βn+1s+βn=(s+ωo)n

(4)

这样表示之后,LESO就只剩下ωo这一个参数,便于观测器的设计以及参数整定。

连续系统非线性ESO的算法为

(5)

式中,β1～βn+1为ESO待调节的参数;a1～an均为[0,1]的可调参数；2δ为线性段的区间长度;fal(·)函数的公式为

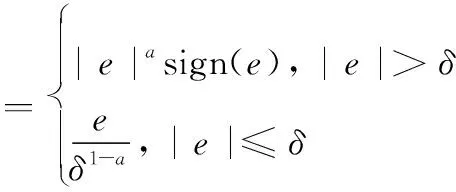
(6)

1.3 状态误差反馈控制律

对于LADRC,用LESO进行动态补偿之后,系统变成积分器串联控制系统,因此只需采用较为简单的线性PD控制律就可以到达控制目的。线性误差控制律算法为

(7)

为了便于控制器的设计以及对参数进行整定,因此希望控制器的参数都只用ωc来进行表示,方法是将系统闭环特征多项式的根全部设置在-ωc处,表示为

sn+kdn-1sn+1+…+kd1s+kp=(s+ωc)n

(8)

以二阶连续系统为例,一种基于fhan(·)函数构造而成的NLSEF,算法为

u0=-fhan(e1,ce2,r2,h2)

(9)

式中,c、r2、h2均为可调参数。

系统最终的控制量u由观测器对扰动的估计值z3来进行补偿，即

(10)

2 四旋翼无人机系统模型

四旋翼无人机系统的结构示意图,如图1所示。

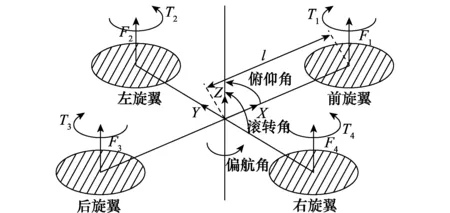
图1 四旋翼无人机系统结构示意图Fig.1 Diagram of quadrotor

四旋翼无人机系统的数学模型[16-17]公式为

(11)

(12)

其他系统参数如表1所示。

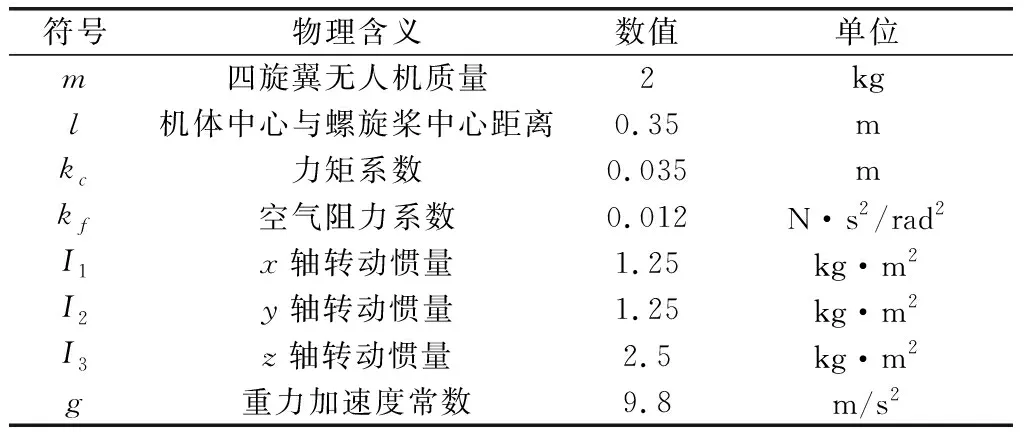
表1 四旋翼无人机系统参数

为了便于四旋翼无人机控制系统的设计以及表示,引入虚拟控制量U1,U2,U3,U4,虚拟控制量与F1,F2,F3,F4之间的变量转换为

(13)

3 四旋翼无人机控制系统设计

四旋翼无人机是由3个位置变量和3个姿态变量组成的6自由度飞行系统,因此可分为位置回路和姿态回路。由于姿态回路控制速度较快,而且可以由虚拟控制量分别独立控制,因此对姿态回路的控制将采用自抗扰控制,位置回路的控制将采用经典的PD控制。

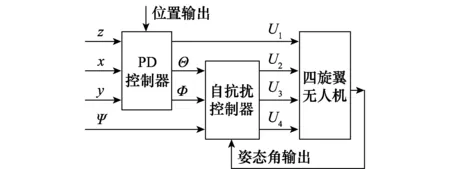
图2 四旋翼无人机控制框图Fig.2 Block diagram of quadrotor control

3.1 姿态回路ADRC设计

四旋翼无人机的姿态回路是由俯仰角、滚转角和偏航角组成,由于引入了虚拟控制量,姿态回路可以分为3个独立的通道且分别由唯一对应的虚拟控制量进行单独控制。为了便于控制器的设计以及参数整定,3个姿态角通道的控制器算法相同且采用相同参数。以偏航角通道为例进行ADRC设计,控制算法为

(14)

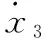
(15)

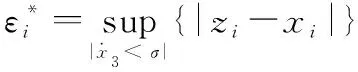
以偏航角通道为例进行LADRC设计,控制算法为

(16)

3.2 位置回路PD控制器设计

位置回路是由高度z,水平位置x以及水平位置y组成的,可以将其分为两个独立的部分,其中高度通道可以由虚拟控制量U1单独控制,水平位置分量x和y分别与姿态角θ和φ相耦合,再分别由姿态回路中的虚拟控制量U2和U3进行控制。

设xd,yd,zd为3个位置的设定值,则高度通道PD控制器算法为

(17)

式中,kpz和kdz分别为高度通道PD控制器的比例参数和微分参数。

水平位置x通道和y通道的PD控制器算法为

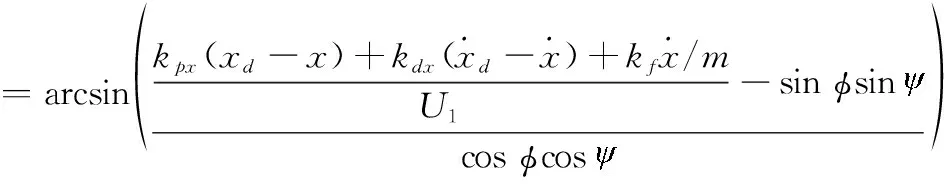
(18)

(19)

式中,kpx,kpy和kdx,kdy分别为通道x和通道y的比例参数和微分参数,uθ和uφ分别为俯仰角θ和滚转角φ的期望轨迹,将θ和φ的期望轨迹输入到姿态回路中就可以得到虚拟控制量U2和U3。

3.3 系统稳定性分析

以偏航角通道为例,其系统模型为

(20)

式中,xi(i=1,2,3)分别为偏航角,偏航角速度以及系统扰动;b0=1。

对偏航角通道设计ESO如式(21)所示,控制器设计如式(22)所示。

(21)

(22)

由式(11)和式(22)可知,偏航角通道的传递函数为

(23)

式中,a=kf/I3。

自抗扰控制器的传递函数可以分成两个部分Gh(s)和Gc(s)[19],系统传递函数方框图如图3所示。

图3 系统传递函数方框图
Fig.3 Block diagram of transfer function

(24)

(25)

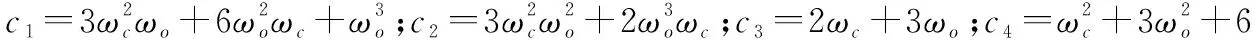
则偏航角通道环路增益传递函数和闭环传递函数为

(26)

(27)

式中,d1=a+c3;d2=ac3+c4;d3=ac4;d4=c1+ac4。因此只要正确选择观测器和控制器的带宽就可以保证系统的稳定性。本文仿真实验取ωo=40,ωc=30,则偏航角通道的伯德图如图4所示,此时的相角稳定裕度为32°。

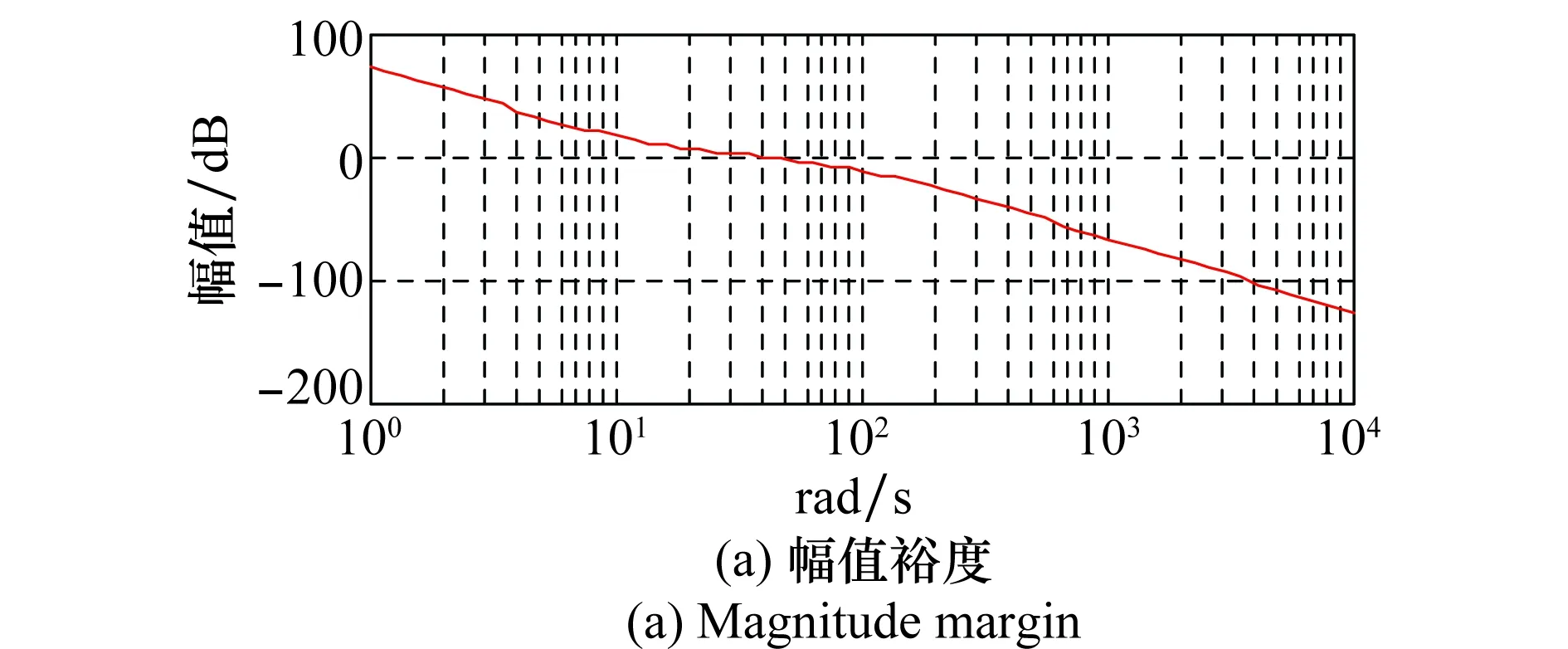
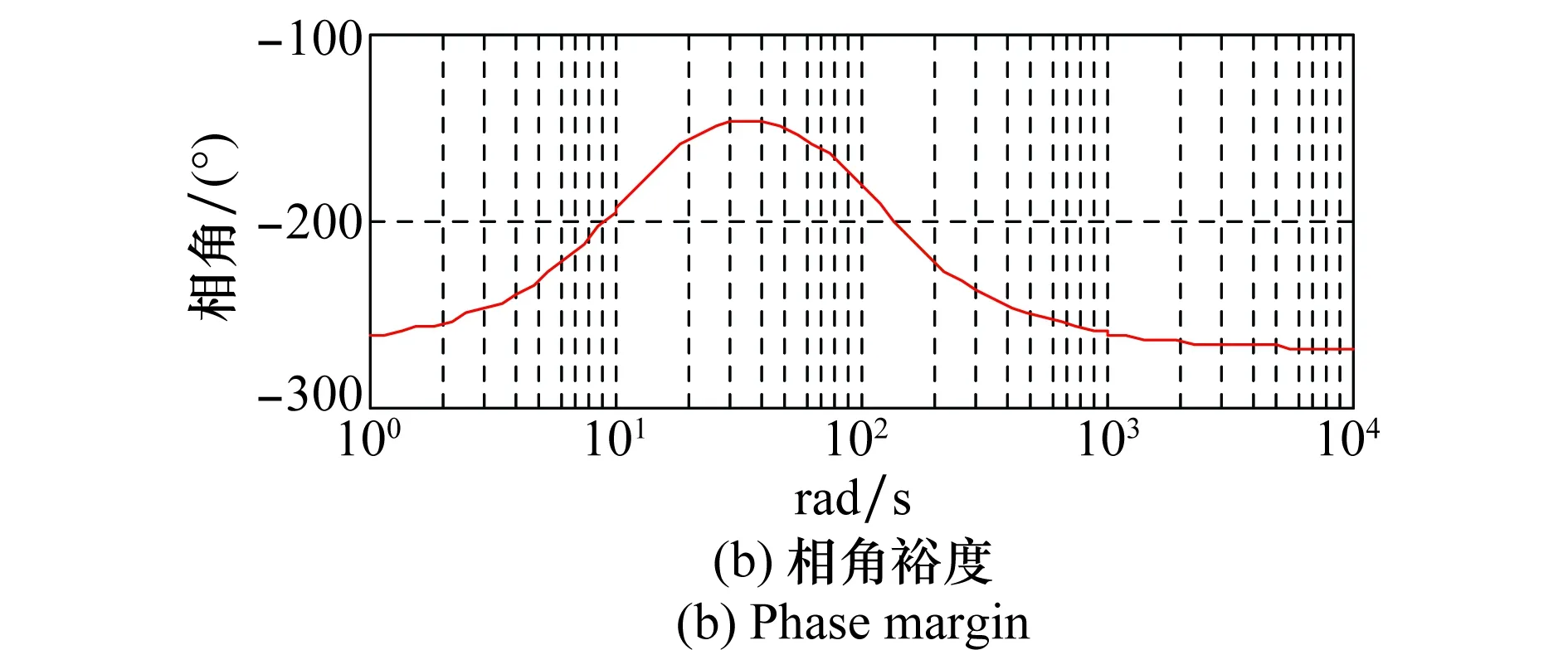
图4 偏航角通道伯德图Fig.4 Bode plot for yaw angle

4 四旋翼无人机系统控制仿真

将根据上文所述的设计方法分别对四旋翼无人机设计PD-ADRC和PD-LADRC,在Matlab环境下进行四旋翼无人机飞行控制仿真,并将两种方法进行对比分析。

4.1 带扰动的四旋翼无人机控制仿真

分别在俯仰角、滚转角和偏航角通道加入扰动ω1(t)、ω2(t)、ω3(t),3个扰动的具体数值为

ω1(t)=sign(sin 0.9t)

(28)

ω2(t)=sign(sin 0.9t)+cos 0.3t

(29)

ω3(t)=0.5sign(sin 0.5t)+cos 0.3t+2cos 0.9t

(30)

PD-ADRC控制系统参数如表2所示,PD-LADRC控制系统参数如表3所示,图5为无人机轨迹跟踪效果图,位置回路控制仿真结果如图6所示,姿态回路控制仿真结果如图7所示。

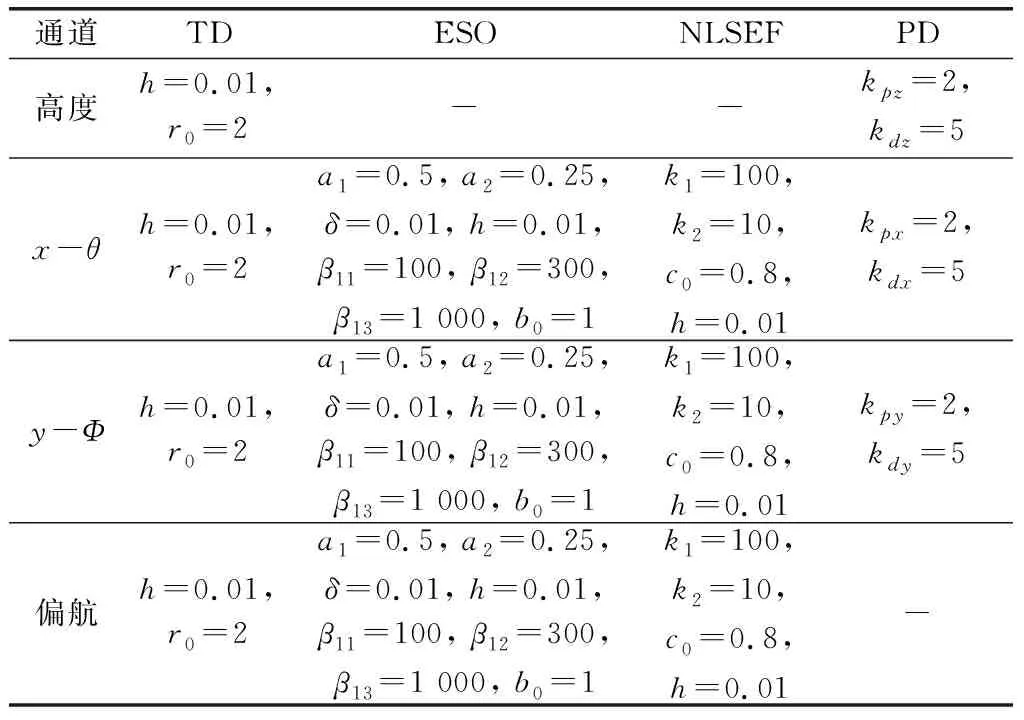
表2 PD-ADRC仿真参数

表3 PD-LADRC仿真参数

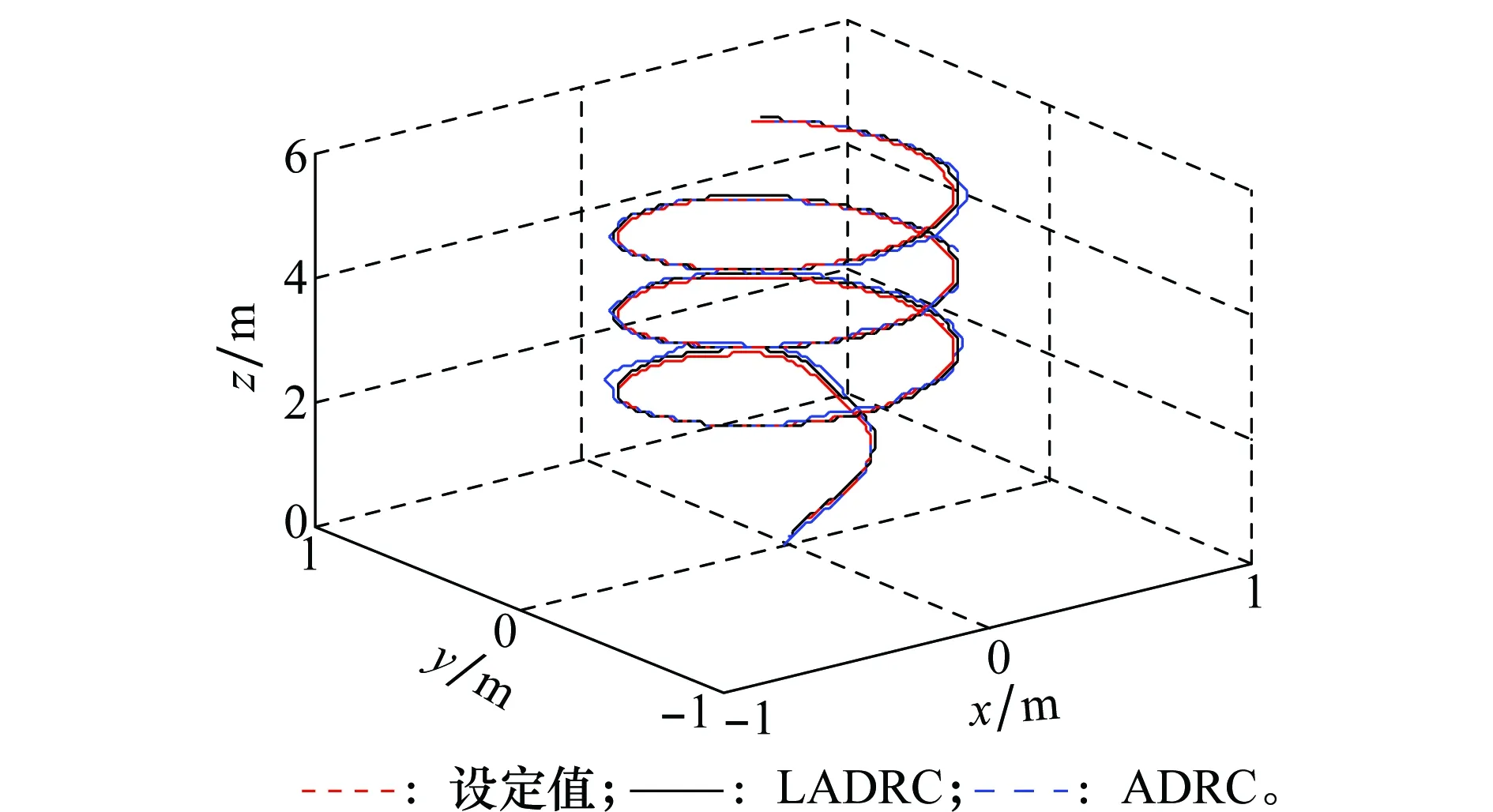
图5 四旋翼无人机轨迹跟踪效果Fig.5 Trajectory tracking of quadrotor

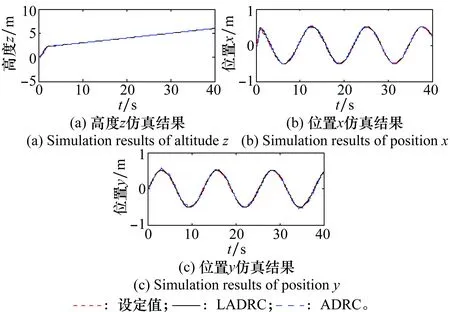
图6 位置控制仿真结果Fig.6 Simulation results of position control

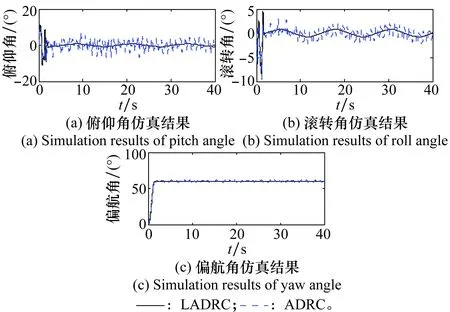
图7 姿态控制仿真结果Fig.7 Simulation results of attitude control

由图5～图7可知,四旋翼无人机加入扰动后,PD-LADRC的轨迹跟踪效果以及位置控制效果依然良好,但是PD-ADRC则出现较为明显的波动,且PD-ADRC对姿态角的控制很不理想,3个姿态角都出现了较大程度的振荡,始终无法稳定在期望值上,而PD-LADRC对姿态角的控制始终非常稳定,控制效果良好。图8和图9分别为两种控制系统的控制量曲线。

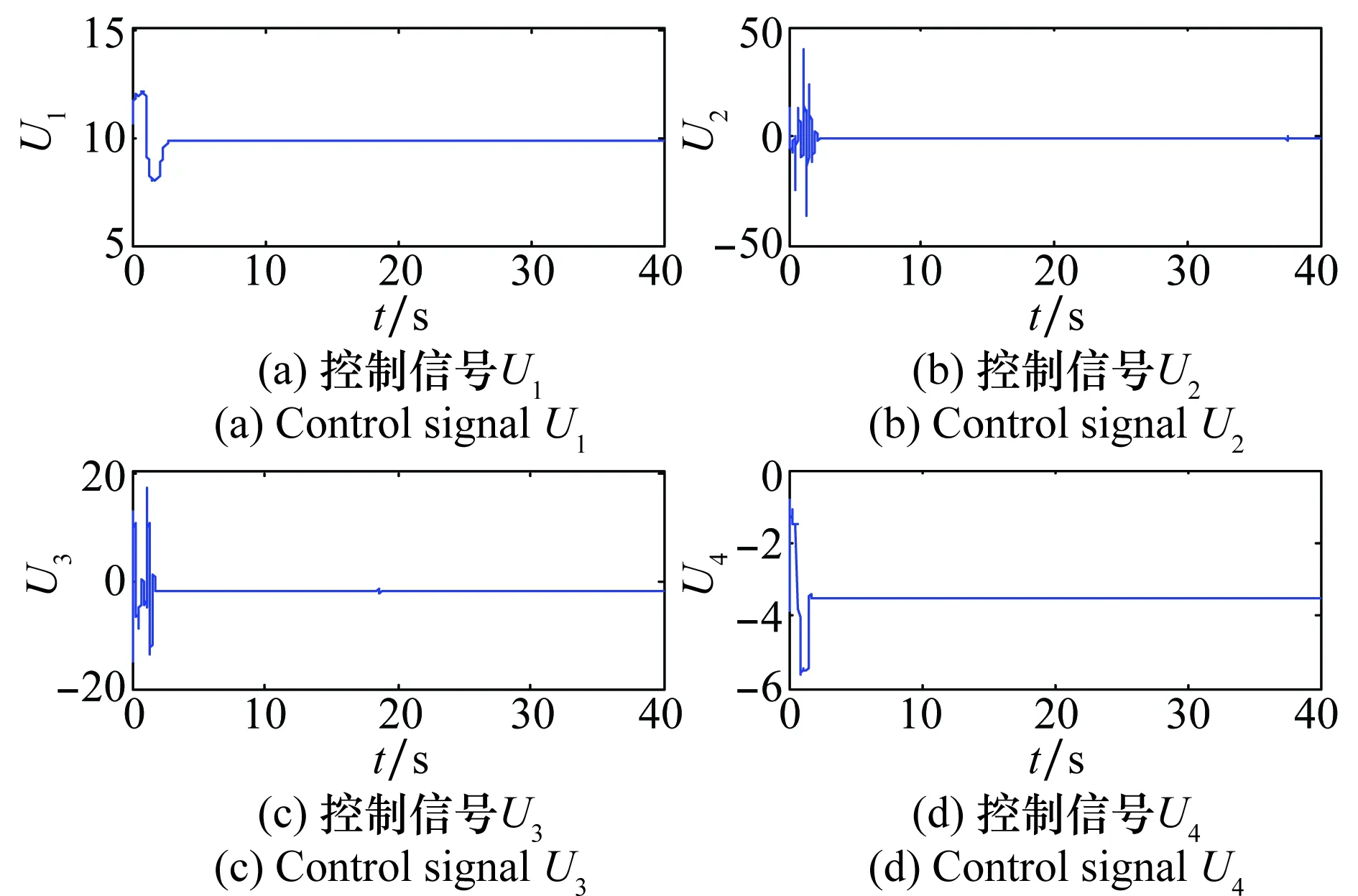
图8 PD-LADRC控制信号Fig.8 Control signal of PD-LADRC

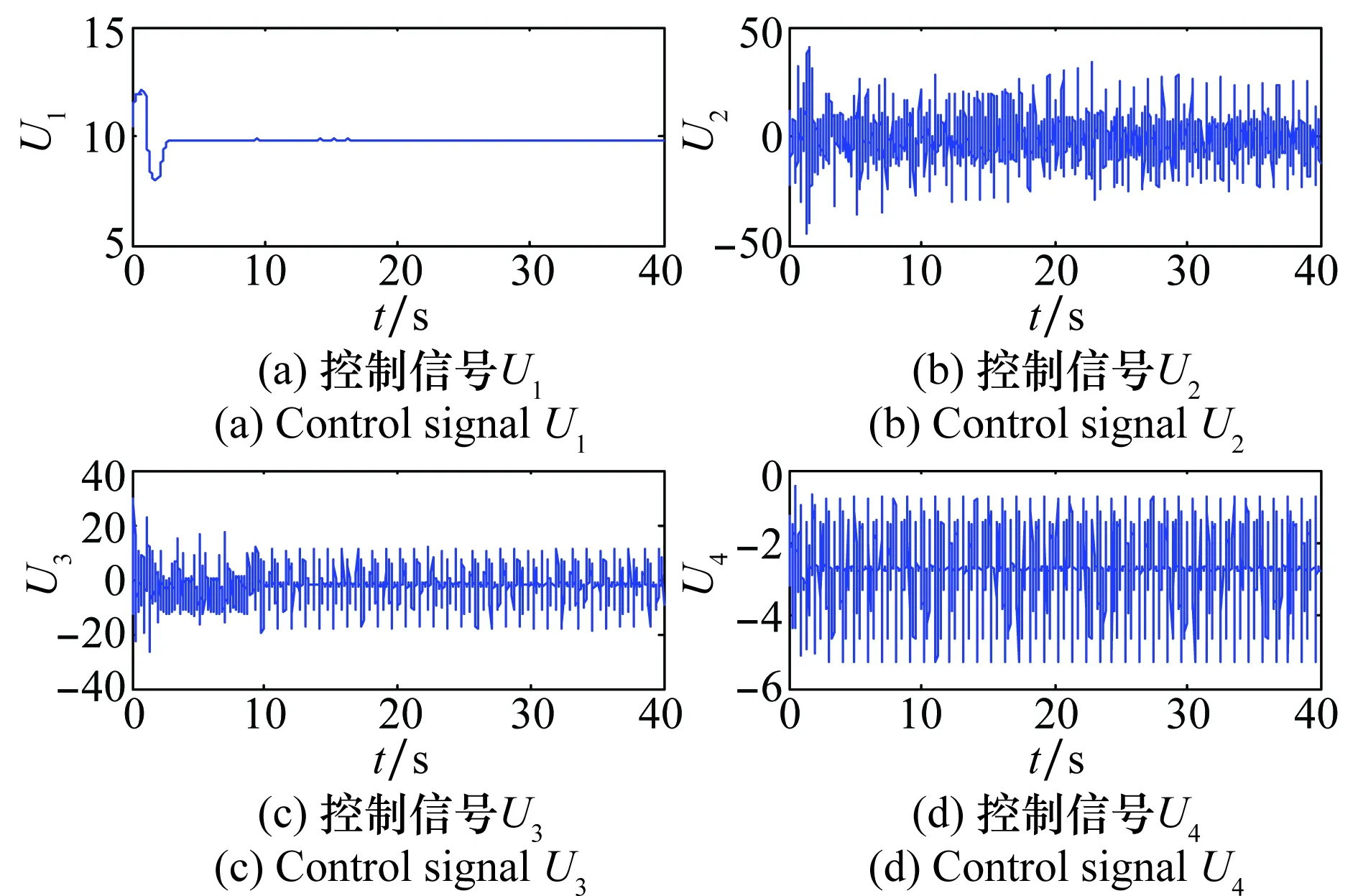
图9 PD-ADRC控制信号Fig.9 Control signal of PD-ADRC

从图8和图9可以看出,PD-LADRC的4个控制量信号都是比较稳定的,没有出现较大波动,但是PD-ADRC的4个控制量中只有U1是比较稳定的,其他3个控制量都出现了明显的振荡,稳定性明显低于PD-LADRC控制系统的控制效果。

4.2 带信号延迟的四旋翼无人机控制仿真

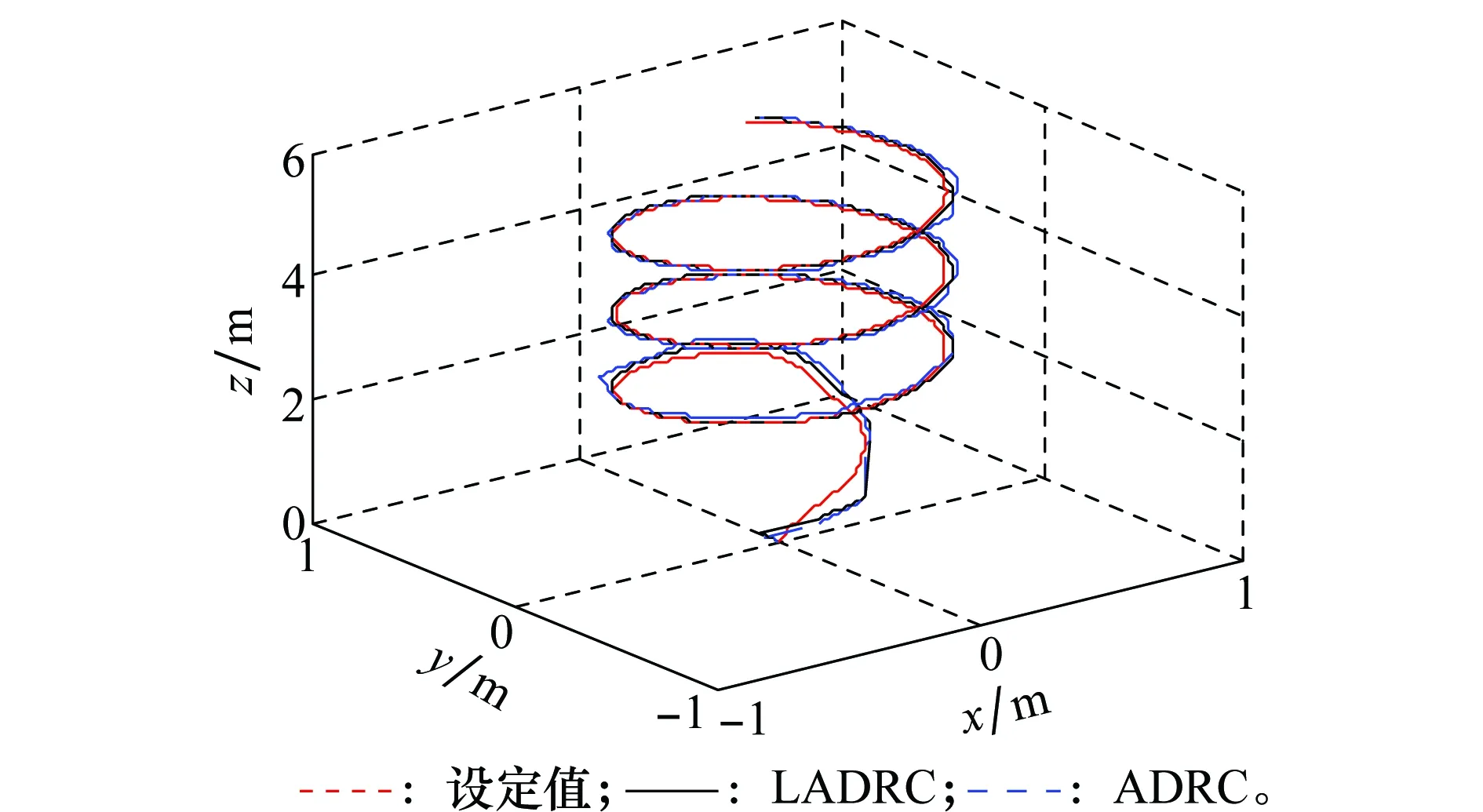
图10 四旋翼无人机轨迹跟踪效果Fig.10 Trajectory tracking of quadrotor

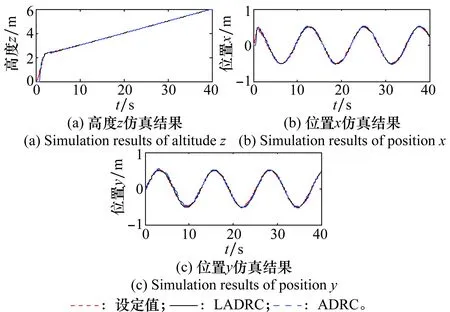
图11 位置控制仿真结果Fig.11 Simulation results of position control

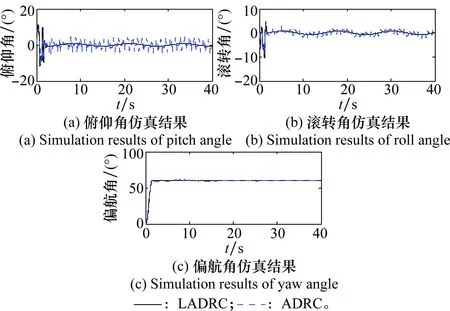
图12 姿态控制仿真结果Fig.12 Simulation results of attitude control

由图10～图12可知,四旋翼无人机的被控量加入延迟后,在保持所有控制器参数不变的情况下,本文设计的控制器仍能保证四旋翼稳定准确地跟踪设定轨迹,说明系统具有一定的稳定裕度,可以保证四旋翼在一定的信号延迟后也能平稳飞行。而且PD-LADRC的控制效果要明显优于PD-ADRC的控制效果,尤其是对姿态角的控制,PD-ADRC控制的3个姿态角同样出现了较大程度的振荡,而PD-LADRC对姿态角的控制始终非常稳定,控制效果良好。

5 结 论

本文针对四旋翼无人机飞行系统,分别设计了PD-ADRC串级控制系统和PD-LADRC串级控制系统。由于PD控制具有控制结构简单实用、参数易调节等优点,因此非常适合应用在通过与位置变量反解得到的角度变量上,而ADRC具有的强解耦能力和对内扰和外扰的估计补偿能力也很好地解决了姿态回路中非线性、多变量以及强耦合等控制问题。对无人机的飞行位置和飞行姿态进行了控制仿真,经过参数整定,获得了良好的仿真结果。对比PD-ADRC和PD-LADRC仿真结果,在四旋翼无人机飞行系统的应用中,LADRC参数少、易整定,且控制精度更高,跟踪速度更快,具有更强的抗干扰能力、鲁棒性,更符合工程实际的需求。