多事件激励的滚动轴承动力学建模
2018-09-27常斌全剡昌锋康建雄吴黎晓
常斌全, 剡昌锋, 苑 浩,3, 康建雄,2, 王 凯, 吴黎晓
(1.兰州理工大学 机电工程学院, 兰州 730050; 2.西安理工大学 机械与精密仪器工程学院,西安 710048; 3.广东鸿铭智能股份有限公司, 东莞 523128)
滚动轴承主要用于支撑旋转部件,是旋转机械的重要组成部分。滚动轴承的使用寿命会直接影响到旋转设备的可靠性,而表面局部缺陷的存在则会明显降低滚动轴承的使用寿命。因此,对滚动轴承局部缺陷进行动力学建模和研究具有十分重要的理论价值和工程应用价值。
滚动轴承在长期工作过程中,会出现点蚀、剥落、裂纹、压痕及磨损等局部缺陷,针对滚动轴承表面局部缺陷的动力学建模研究,已经取得了大量的成果。 Walters[1]首次建立了陀螺仪中的球轴承的动力学模型,研究了滚子与保持架的动态变化。Sunnersjö[2]探讨了滚动轴承的变刚度振动问题,研究了滚动轴承正常运行过程中产生振动的原因。研究表明,滚动轴承受载的滚动体数量变化、轴承的制造和安装误差都会产生变刚度振动,且变刚度振动是不可避免的。随后,学者们对存在表面局部缺陷的滚动轴承的振动机理展开了深入地研究。
Patil等[3]建立了一个2自由度的缺陷滚动轴承动力学模型,研究了滚道表面局部缺陷大小、缺陷位置对轴承动态性能的影响规律。Patel等[4]建立了考虑轴、保持架、滚道及球质量的两自由度动力学模型,分别研究了内、外滚道表面单故障及多故障诱发的轴承振动响应。杨将新等[5]综合考虑了轴承载荷分布、故障冲击脉冲序列、系统刚度及损伤部位的位置变化等参数对系统振动特性的影响,建立了内圈局部损伤滚动轴承系统的振动模型。Rafsanjani等[6]考虑了非线性赫兹接触变形和径向游隙的影响,建立了一个表征滚动轴承表面局部缺陷的非线性动力学行为的分析模型。刘静等[7-8]提出考虑滚动体与滚道之间非理想Hertz线接触特性和时变位移激励的圆柱滚子轴承局部缺陷动力学模型,研究了局部缺陷尺寸和位移激励形式对圆柱滚子轴承振动特性的影响规律。Nakhaeinejad等[9-10]采用多体动力学方法建立了缺陷滚动轴承的动力学模型。Sawalhi等[11-12]在实验中观察到了双脉冲现象并用多体动力学模型进行了仿真。张建军等[13-15]引入单元谐振器模拟了故障轴承元件的高频固有振动,探索了故障轴承组件高频共振的产生机理。赵联春等[16-17]考虑了弹流润滑对轴承接触刚度的影响,建立了故障轴承动力学分析模型。Cao等[18-20]发展了Gupta模型,建立了考虑滚动轴承各组件三维运动的动力学分析模型。这些分析模型尽管考虑的因素越来越全面,对滚动轴承的故障信息的描述也越来越准确,然而,大多数模型并没有考虑轴承元件局部缺陷引起的冲击激励,虽然有少数研究考虑了缺陷引起的冲击激励,但也只是基于缺陷轮廓形状的简单描述或者将冲击激励采用单一的半正弦函数来表征。
当轴承滚动体通过滚道的表面局部缺陷区域时,就会产生包含缺陷特征的冲击响应信号。Mcfadden等[21]采用Dirac Delta函数构造了一个周期性的等幅力脉冲有限序列来表征点缺陷引起的冲击激励。Epps[22]构造了一个分段的激励力函数并对其进行了分析。Tandon等[23-24]采用三角形、矩形和半正弦等不同轮廓形态的函数定义局部故障引起的冲击激励力。Singh 等[25]利用多事件分析了滚动体与滚道间的接触力的变化情况。Khanam等[26-27]分别分析了滚动轴承外圈和内圈表面局部缺陷上的激励力,并细化了滚动体进入和离开缺陷的激励过程,提出了一个多事件激励力模型。
以上研究从多个层面探究了滚动轴承故障产生的机理和故障引起的动力学特性,但对表面局部缺陷引起的力激励和时变位移激励机理的研究还需作进一步的深入探讨。本文以深沟球轴承为研究对象,在Khanam模型的基础上,描述了滚动体经过缺陷区域的多事件情形,考虑了冲击激励和缺陷与轴承变刚度振动引起的时变位移,建立了内圈表面存在局部缺陷的滚动轴承动力学模型并进行了验证。
1 多事件激励
假设轴承座与外圈紧密配合,内圈随轴一起转动且与轴之间无相对位移。内圈表面存在局部缺陷,且缺陷的宽度小于滚动体的直径,缺陷有一定的深度,使得滚动体在滚过缺陷的过程中接触不到缺陷底部。由于缺陷的存在,每个滚动体经过缺陷(图1所示,假设第i个滚动体球心经过A-B-C,并继续沿滚道滚动,直至第i+1个滚动体进入缺陷)的过程中会经历四个事件(如图2所示),分别是:进入事件、撞击事件、离开事件和载荷补偿事件。
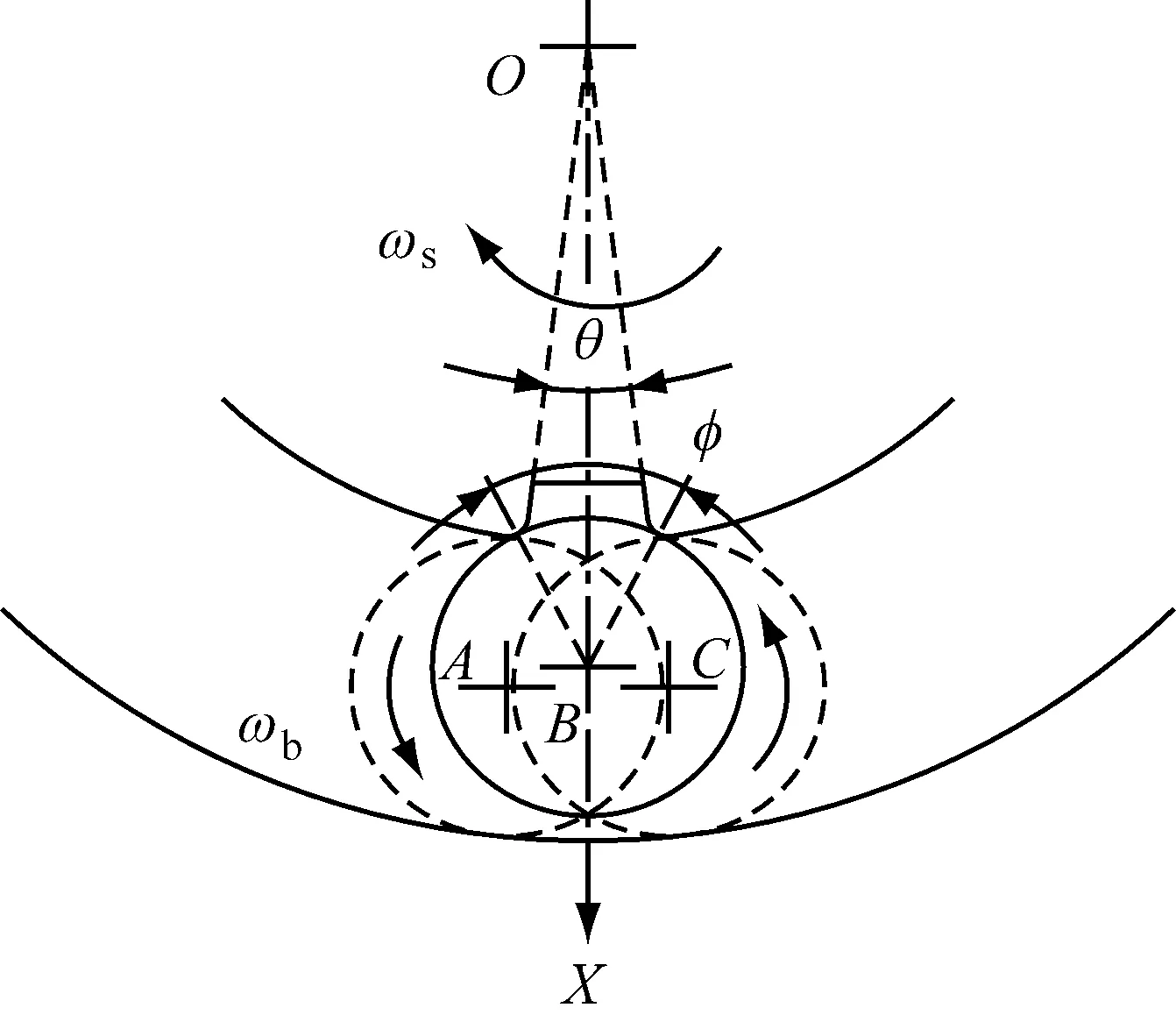
图1 滚动体经过缺陷时的几何模型Fig.1 Geometric model of rolling element passing defect
1.1 进入事件
假设缺陷边缘的形貌是微小的圆弧状,记滚动体进入缺陷时经过的缺陷边缘为缺陷始边,离开时经过的缺陷边缘为缺陷终边,同时假设缺陷始边和缺陷终边的圆弧曲率半径相同,都约等于滚动体半径的1/20。如图2(a)所示,当滚动体沿内滚道靠近缺陷始边位置时,滚动体所承受的内外滚道之间的接触力会开始变小。从此刻开始,就意味着滚动体开始进入缺陷。接着,滚动体沿着缺陷始边的圆弧继续运动,直至经过角度η后,滚动体与外滚道的接触力完全变为0。这个过程就是进入事件。
根据赫兹接触理论的载荷—变形关系,进入力Fe力可以通过下式计算
(1)
式中,载荷-位移系数k为
(2)
进入最大位移量xemax为
(3)
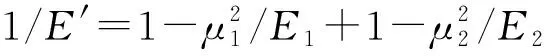
进入缺陷的时间te为
te=η/20(ωb+ωs)
(4)
式中:η为进入角;ωb,ωs分别为球和转轴的角速度。

(a) 进入事件
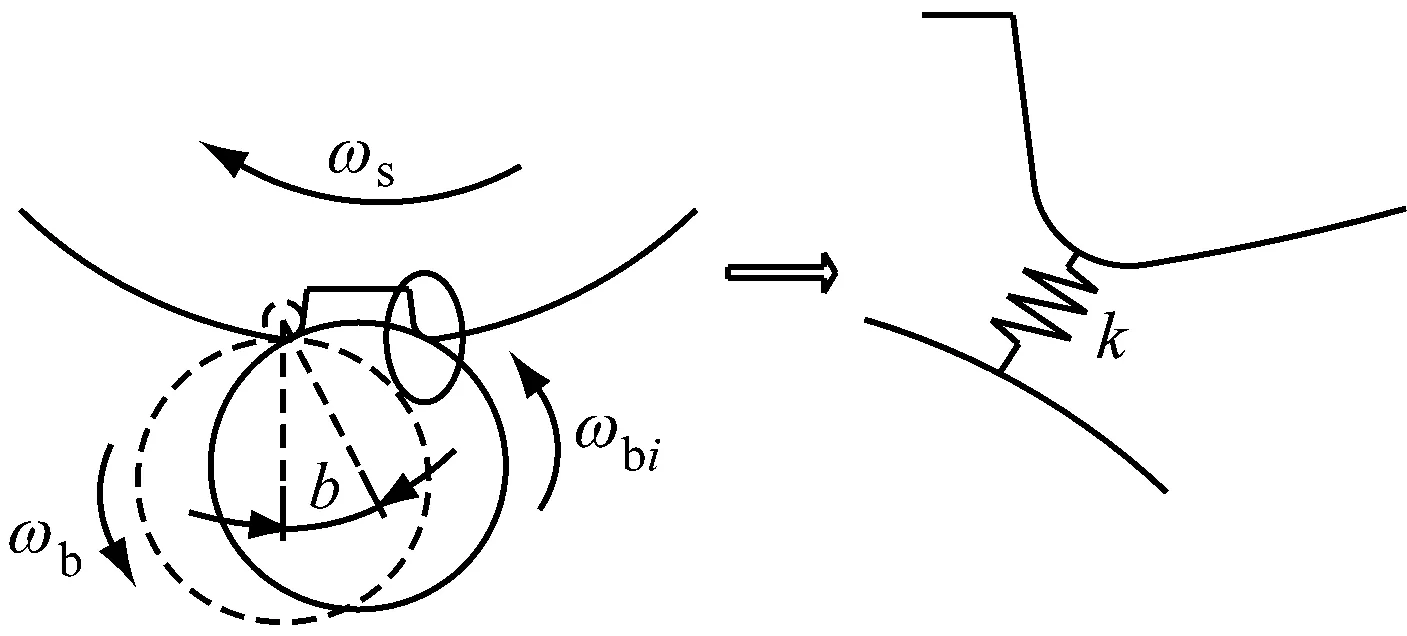
(b) 撞击事件
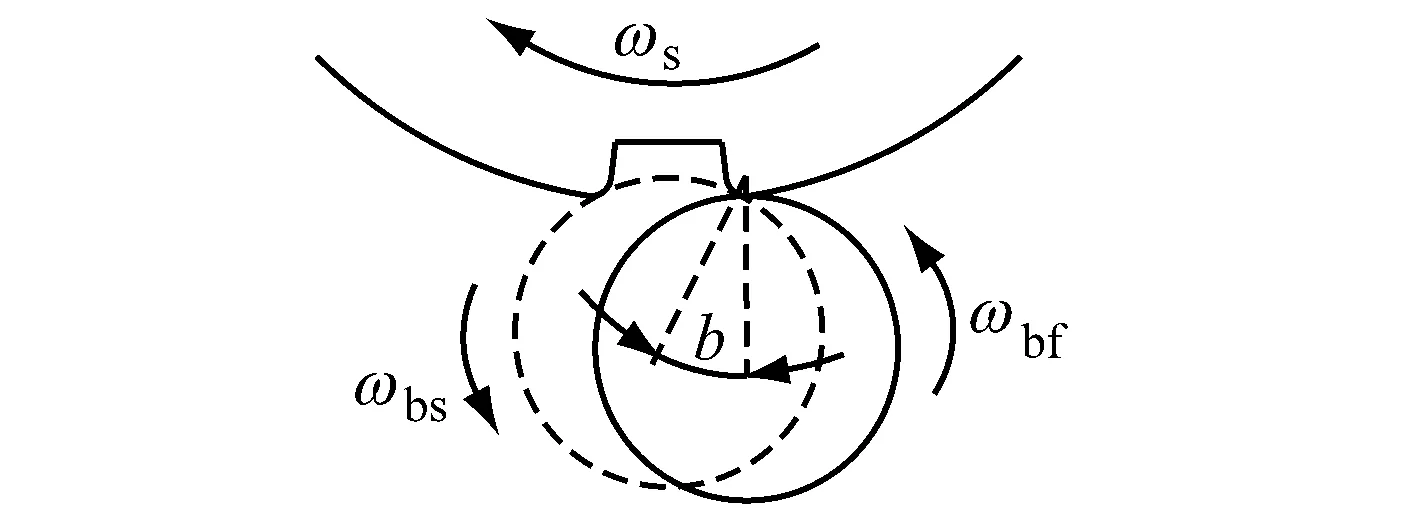
(c) 离开事件
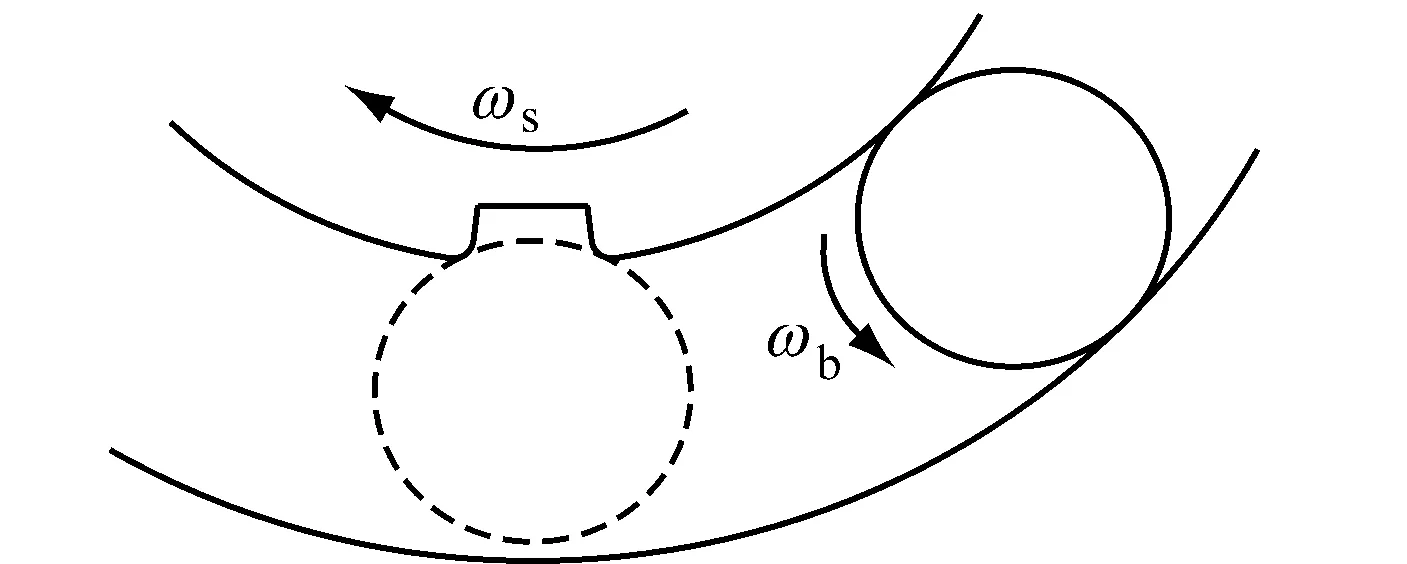
(d) 载荷补偿事件图2 多事件示意图Fig.2 Multi-event schematic diagram
1.2 撞击事件
经过进入事件后,假设滚动体以其与缺陷始边接触的位置为铰接点,向着缺陷终边作铰链旋转运动,直至滚动体撞击到缺陷终边,开始进入撞击事件。则进入事件与撞击事件的时间间隔tg为
tg=wd/2πDi(ωs-ωc)
(5)
式中:wd为缺陷宽度;Di为内圈直径;ωc为保持架的角速度,由下式计算
ωc=ωs/2(1-db/Dp)
(6)
式中:db为滚动体直径;Dp为轴承节圆直径。
在撞击事件中,由于滚动体撞击缺陷终边,造成了瞬时的突然的冲击变形,可以把两表面之间的瞬间撞击情形简化成具有一定刚度的弹簧连接,如图2(b)所示,即撞击过程包含有弹簧的压缩和伸长。
撞击力Fi由式(7)确定
(7)
式中:撞击时弹簧k(如图2(b)所示)的最大形变ximax由下面的方程求得
(8)
式中:m为单个滚动体的质量;v0为t=0时刻,球质心处的线速度,可以由式(9)表示
v0=(R3ωs-R1ωbi)sinφ
(9)
式中:R3为缺陷滚道半径。
撞击时滚动体的角速度ωbi为
(10)
撞击过程中,撞击力由0增加至最大值,再由最大值变到0,这两个过程分别耗时为t1和t2,则撞击时间ti为
ti=t1+t2
(11)
式中,
(12)
t2=2β/(ωbs+ωbf+2ωs)
(13)
式中:β为球质心相对于缺陷始边或终边曲率中心的旋转角度;ωbs,ωbf分别为球沿缺陷终边运动的初始角速度和球质心旋转β角度后的角速度,通过式(14)和(15)来计算
ωbs=ωbicosφ
(14)
(15)
1.3 离开事件
当滚动体经过撞击事件后,滚动体会沿着缺陷终边运动,直至彻底离开缺陷,此时,该滚动体与内外滚道之间的接触力恢复到没有缺陷时的状态,这个过程就是离开事件。
1.4 载荷补偿事件
滚动体经过离开事件后,继续沿着轴承滚道运动,直到下一个滚动体开始进入缺陷时,作用在该滚动体上的载荷会重新分布,轴承的载荷从此前的由Z个滚动体承受变为此刻的由Z-1个滚动体承受。明显的,单个滚动体所承受的载荷会变大。这个过程就是载荷补偿事件。
2 时变位移
时变位移由两部分组成:一部分是由缺陷存在引起的,一部分是由轴承的变刚度振动引起。
2.1 缺陷引起的时变位移
滚动体经过缺陷时,径向位移会发生变化,当滚动体的质心恰好位于缺陷宽度一半的位置时,如把此时的位移变化量记为Hr,如图3所示,根据几何位置关系,有
(16)
滚动体从进入缺陷到离开缺陷,径向位移会经历从0增大至Hr,再由Hr变为0的过程,该过程可以用正弦曲线近似表征,则由缺陷引起的径向位移变化Hd为
(17)
式中:θ=wd/R3为缺陷角;θil为第i个球与内滚道的接触角,其表达式为
θil=2π(i-1)/Z+(ωc-ωs)t
(18)
式中:θi0=2π(i-1)/Z+θ1为局部缺陷相对于第i个球之间的初始角位置;θ1为局部缺陷与第1个球间的初始位置角。
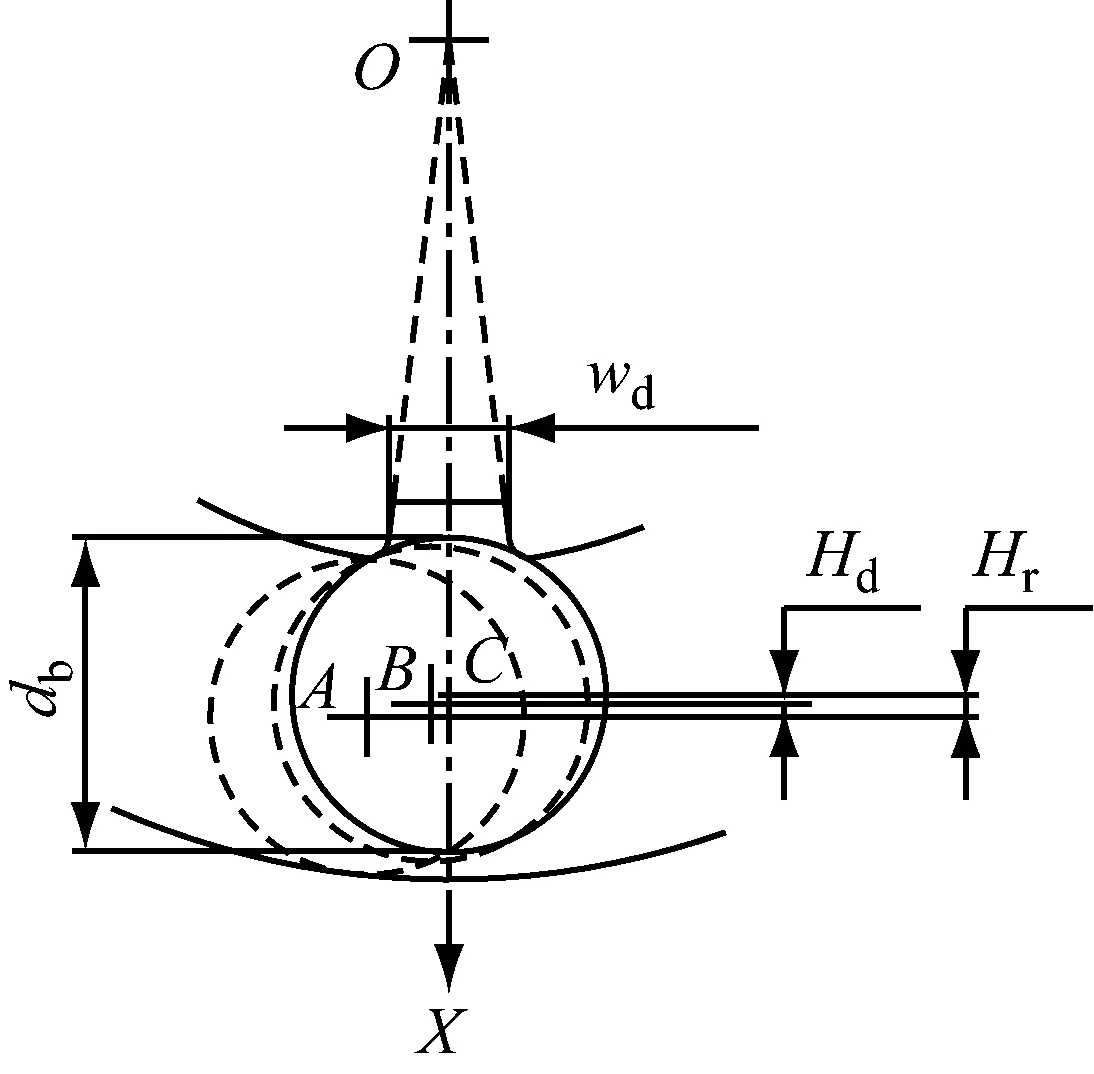
图3 缺陷引起的位移变化说明图Fig.3 Illustration of displacement change caused by defect
2.2 轴承变刚度振动引起的时变位移
滚动轴承运行过程中会产生振动,这是由实际承受外部载荷的滚动体数量发生变化所导致。研究表明,承受外部载荷的滚动体数量会随保持架角位置的变化而变化。这样,轴承组件的总刚度就会产生周期性的变化,由此便产生了变刚度振动。
如图4所示,轴承的变刚度振动会引起水平方向和竖直方向上位移的变化,且这种变化是随时间的非线性变化。轴承发生变刚度振动时,滚动体与滚道之间的接触变形Δ是内圈水平位移y、竖直位移x,第i个滚动体的角位置θi以及径向游隙Cr的函数。根据几何位置关系,可以得到
Δ=xcosθi+ysinθi-Cr
(19)
式中:Cr为径向游隙;θi为任意时刻第i个滚动体的位置角,其表达式如下
θi=2π(i-1)/Z+ωct+θ1x
(20)
式中:θ1x为第1个球相对于x轴的初始位置角,这里取θ1x=0;Z为滚动体总数。
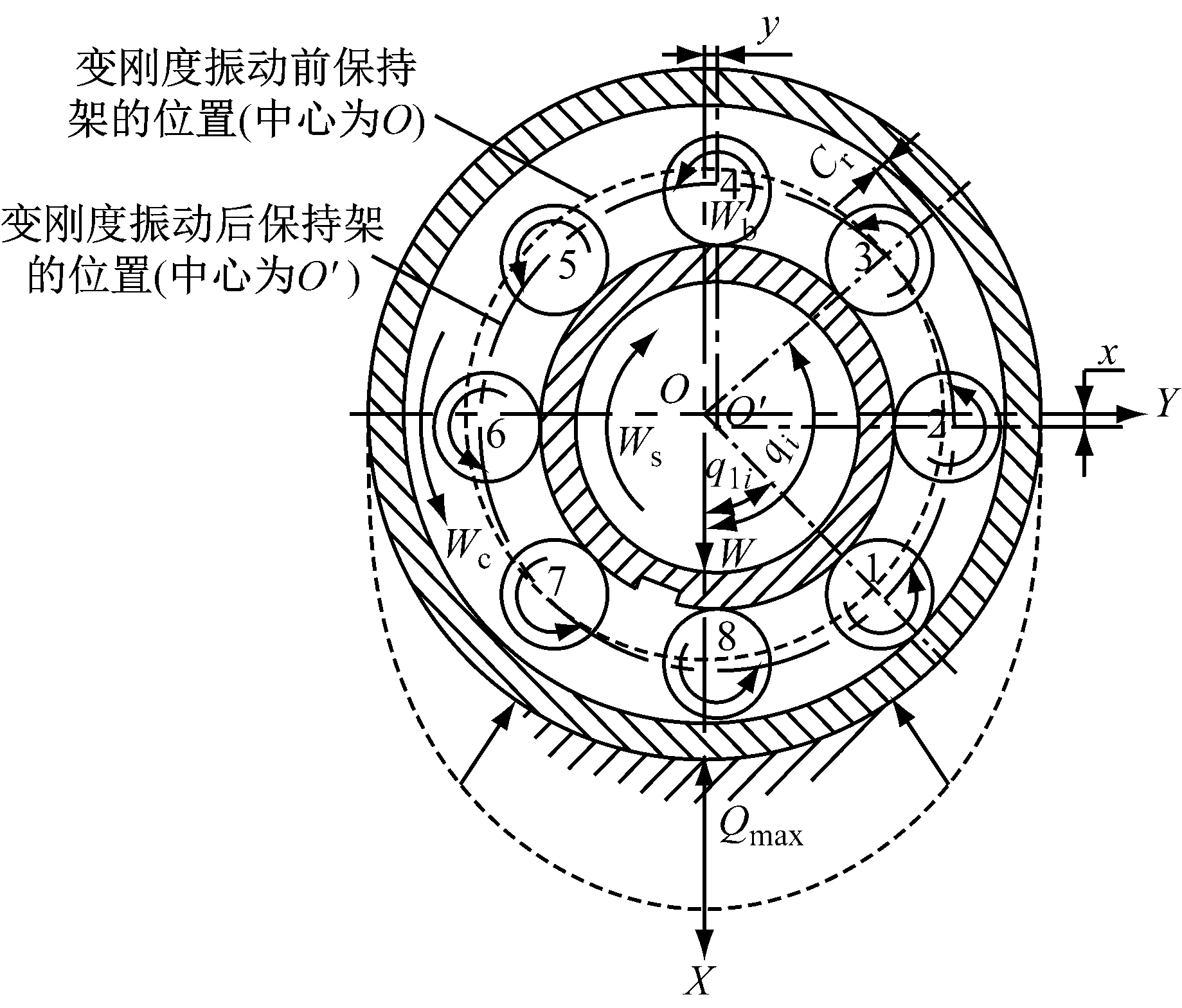
图4 滚动轴承的变刚度振动Fig.4 Diagram of varying compliance vibration of rolling bearing
3 动力学方程
滚道表面存在局部缺陷的滚动轴承在运行过程中,滚动体与滚道之间存在着由时变位移引起的非线性弹性接触力,同时,还存在着由滚道表面局部缺陷诱发的多事件激励力。本文通过分析滚动体经过缺陷的多事件激励情况和轴承径向时变位移的变化情况,将滚动轴承中的每个滚动体都简化为一个并联的有质量的弹簧-阻尼系统,建立了一个2自由度的内圈表面存在局部缺陷的滚动轴承动力学模型(如图5所示)。
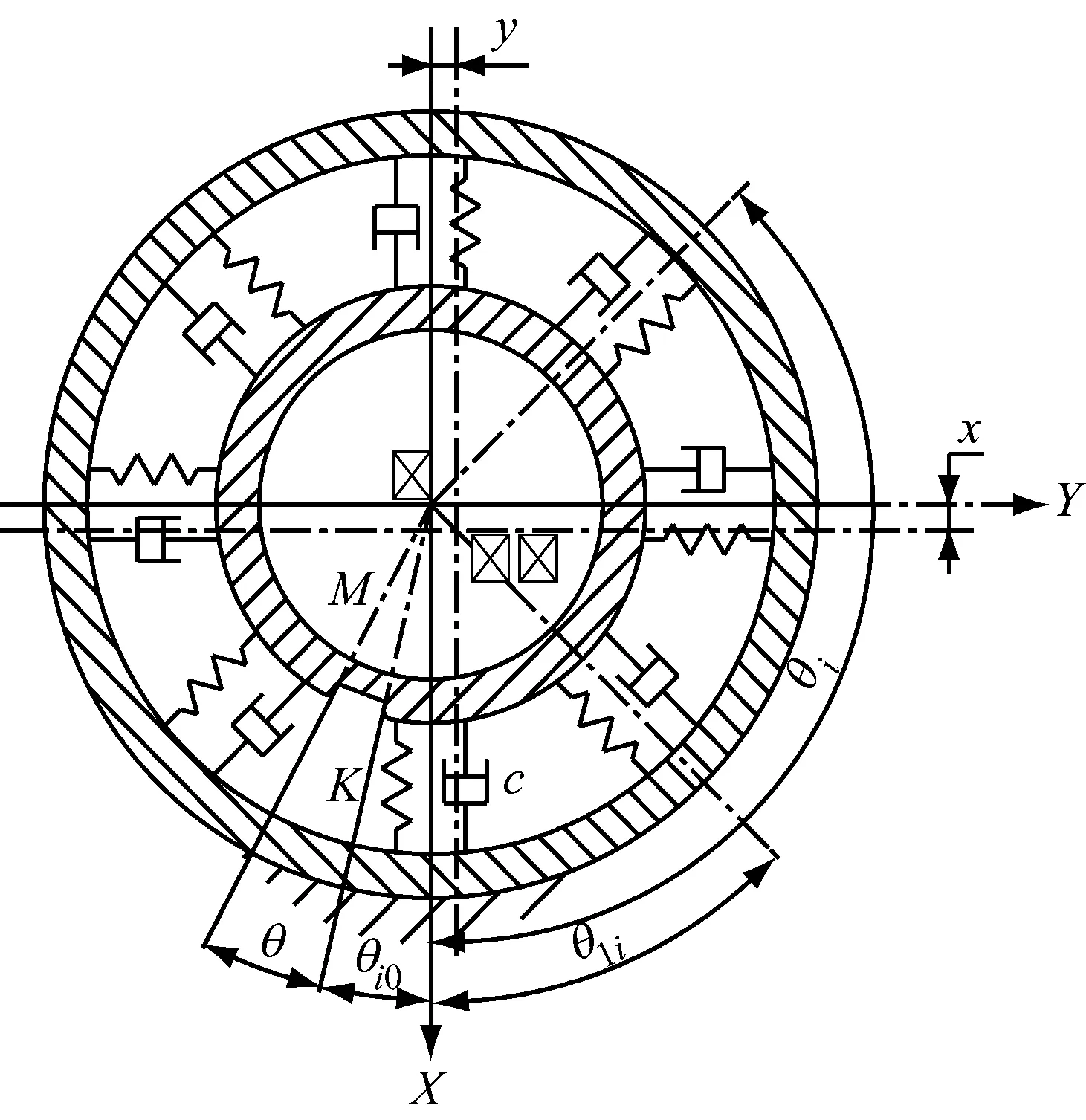
图5 深沟球轴承动力学模型图Fig.5 Dynamics model of deep-groove ball bearing
由牛顿第二定律得,内圈表面存在表面局部缺陷的滚动轴承的动力学方程为
Hd]1.5cosθi+F(t)cosωst=Wx
(21a)
Hd]1.5sinθi+F(t)sinωst=Wy
(21b)
式中:Wx,Wy分别为竖直方向和水平方向上滚动轴承系统的外加载荷。
第i个滚动体的载荷区系数ζi、激励力函数F(t)以及滚道间的总刚度K分别由式(22)、(23)和(24)确定。
(22)
F(t)=f(ωidt)Q(ωst)
(23)
式中:f(ωidt)是与特征缺陷频率ωid有关的量,其由进入与离开缺陷时的激励力脉冲形状所决定,这里假设进入事件中激励力形状为斜直线,而撞击事件中激励力的形状为抛物线;Q(ωst)为在径向载荷作用下滚动体承受的载荷。
(24)
式中:Ki,Ko分别为滚动体与内、外滚道的接触刚度,对于球轴承n=1.5。
4 模型验证
4.1 实验设备
通过凯斯西储大学(Case Western Reserve University)的缺陷轴承响应数据来验证模型。如图6所示,试验台由一个2马力的电动机(左),一个扭矩传感器/编码器(中心),测功机(右)和控制电子(未显示)组成。使用加速度计对振动数据进行测量,加速度计放置在电机外壳的驱动端的十二点钟位置。振动信号是通过一个16通道的DAT记录仪收集,并在MATLAB环境下进行处理。试验采样频率为48 kHz,收集了测试电机在不同转速和试验轴承不同故障尺寸的实时数据。

图6 凯斯西储大学试验台Fig.6 Test rig in Case Western Reserve University
实验采用SKF 6205-2RS型深沟球轴承,具体参数见表1。将该轴承安装在测试电机的主轴上,且轴承外圈固定,内圈随轴一起转动。试验轴承的故障是通过电火花加工而产生的单点人为故障。试验测试了内圈故障尺寸分别为0.177 8 mm、0.355 6 mm和0.533 4 mm,电动机转速分别为1 797 r/min、1 772 r/min、1 750 r/min和1 730 r/min时的故障轴承的加速度信息。
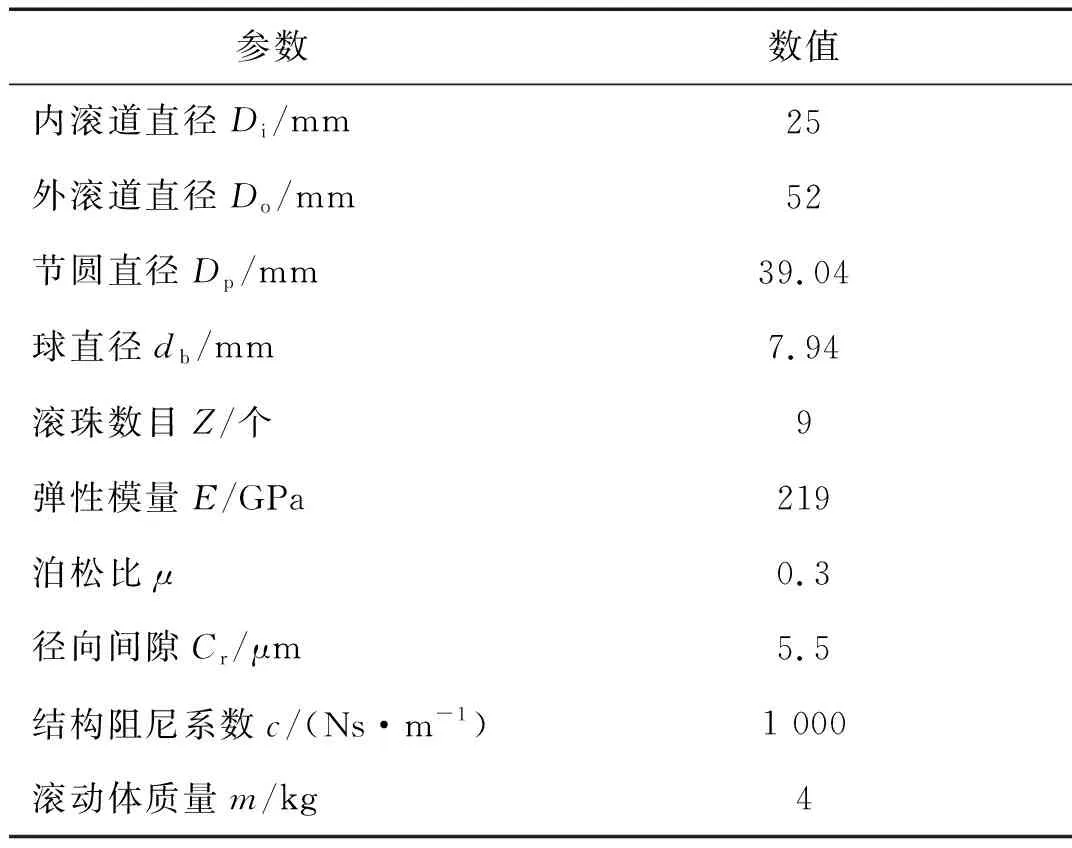
表1 SKF 6205-RS型深沟球轴承参数Tab.1 Deep groove ball bearing parameters of SKF6205
4.2 模拟验证
对于试验数据,运用Protrugram方法[28]选取合适的带宽和中心频率;通过带通滤波器,把采集到的原始信号中的含有故障成分的高频信号从中分离出来;然后将高频信号进行平方包络,从而得到故障信号的时域图;最后将故障信号进行傅里叶变换,得到相应的频谱图。
4.2.1 不同缺陷尺寸的影响
轴承主轴转速为1 750 r/min,缺陷尺寸分别为0.177 8 mm、0.355 6 mm、0.533 4 mm时的缺陷轴承的振动响应如图7、图8和图9所示。其中,每个缺陷尺寸下都用4幅图来表征。第一幅图是试验信号在时域上处理后的结果图;第二幅图是第一幅图经过傅里叶变换后的频域图;第三幅图是模型仿真信号出的时域图;第四幅图是模型仿真信号在频域上的加速度和频率的变化关系图。
从图7、图8和图9中可以看出,试验的故障轴承信号在时域上存在明显的周期性冲击现象;且缺陷尺寸越大,其周期性的冲击振动在时域上愈加地明显,当缺陷较小时,冲击成分几乎淹没在正常的谱线中。在频域上,模型仿真信号图上的转频、特征缺陷频率及其二倍频和它们周围的边频带清晰可见;试验信号图的转频、特征缺陷频率同样清晰可见,但是特征缺陷频率的二倍频不突出,同时,特征缺陷频率及其二倍频周围的边频带分布并无明显规律。
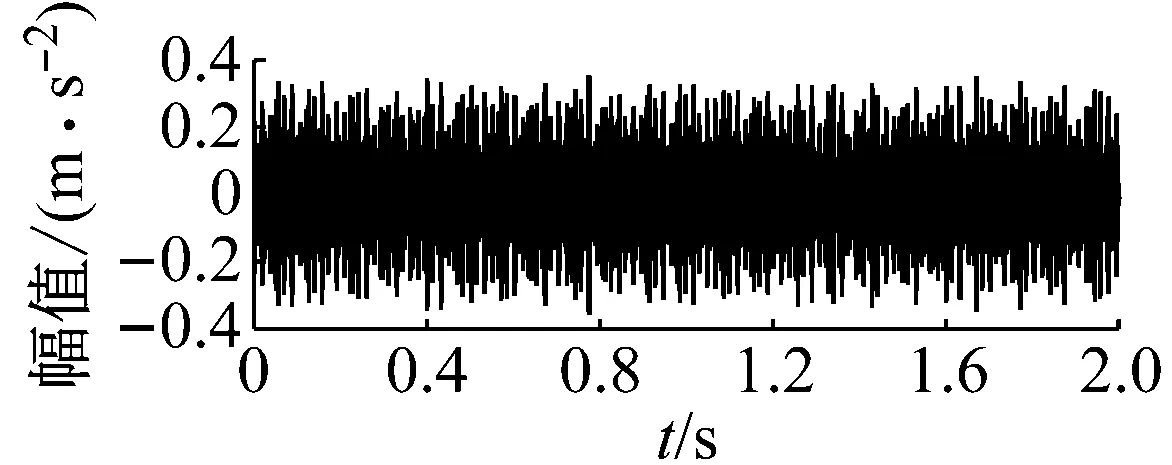
(a) 试验信号时域图
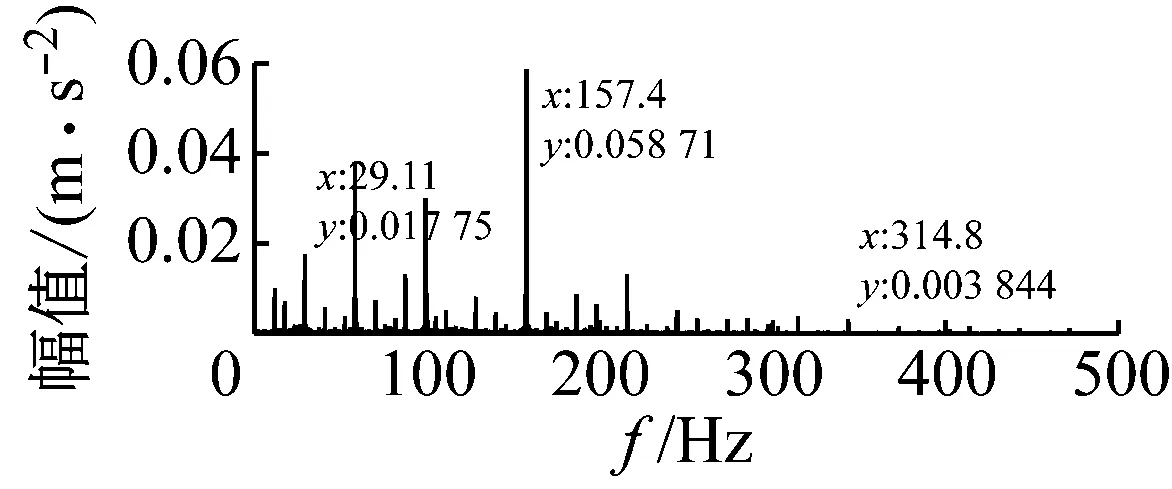
(b) 试验信号频谱图
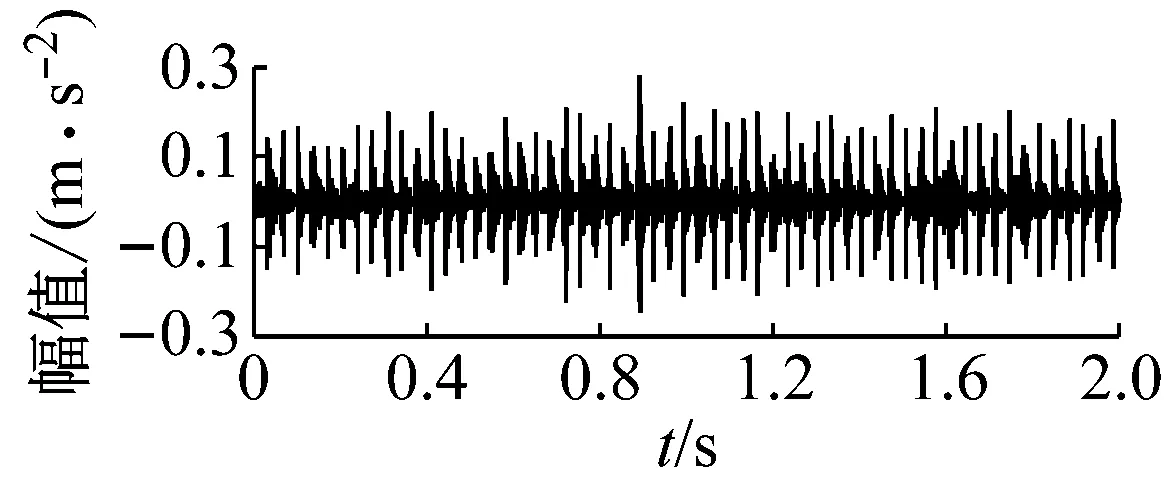
(c) 模型仿真信号时域图
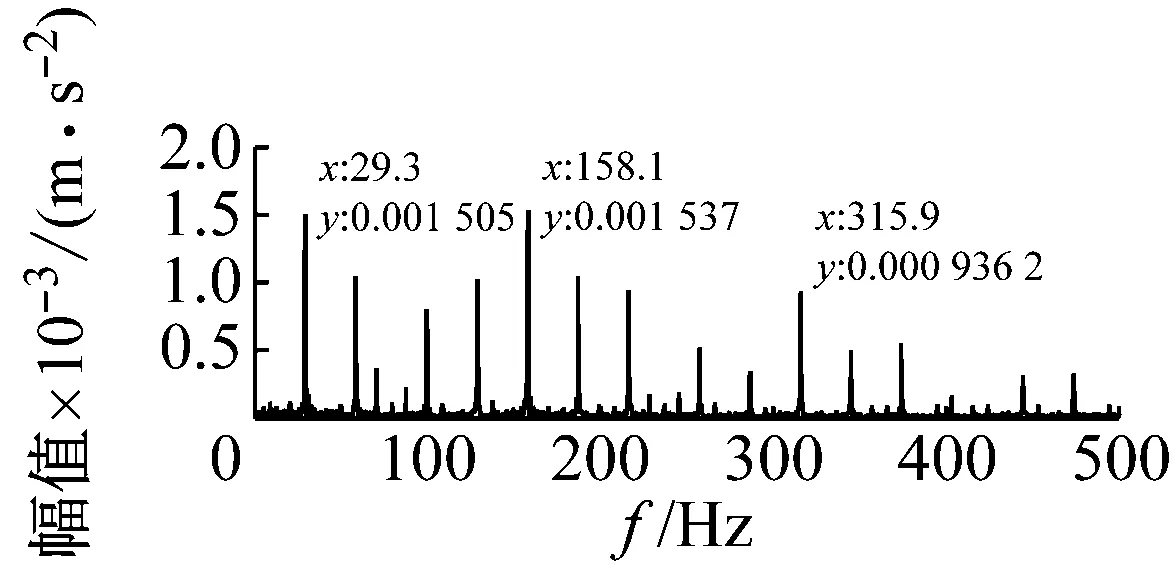
(d) 模型仿真信号频谱图
图7 缺陷尺寸为0.177 8 mm时的试验信号与模型仿真信号图
Fig.7 Signal spectrum of simulation and experiment under 0.177 8 mm defect size
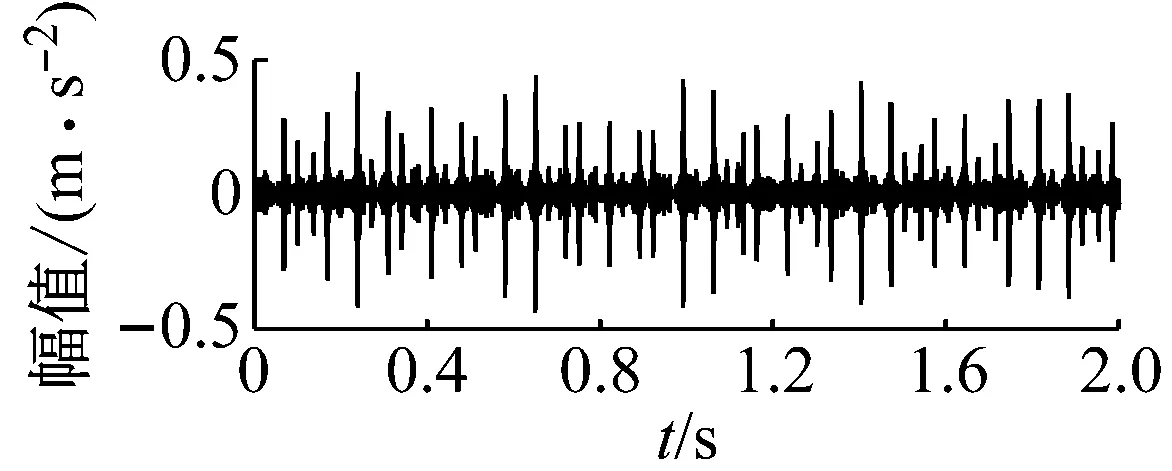
(a) 试验信号时域图
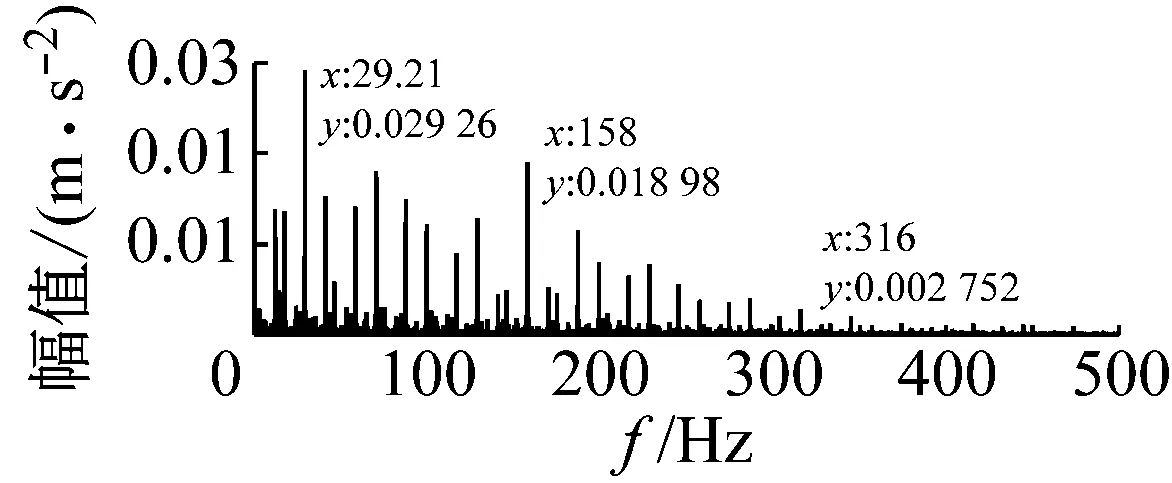
(b) 试验信号频谱图
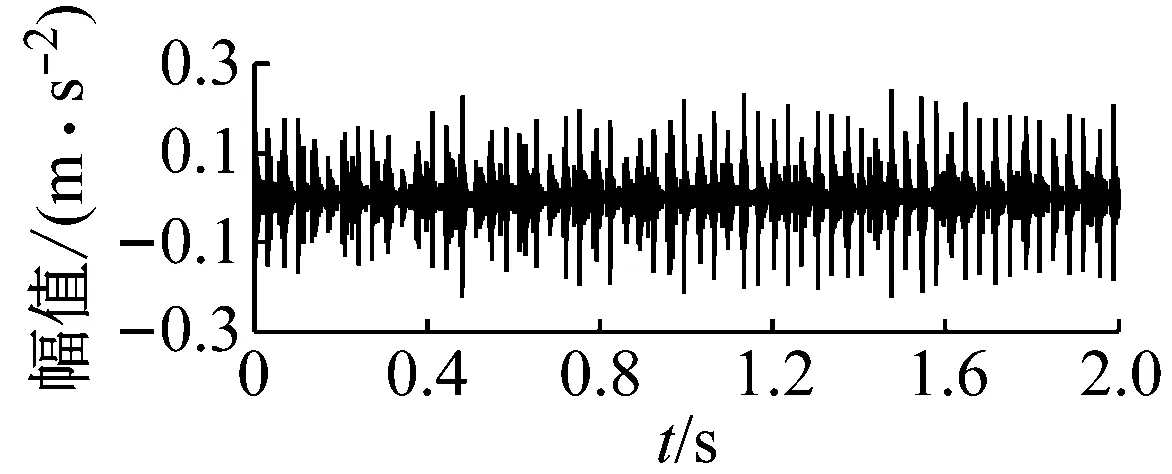
(c) 模型仿真信号时域图
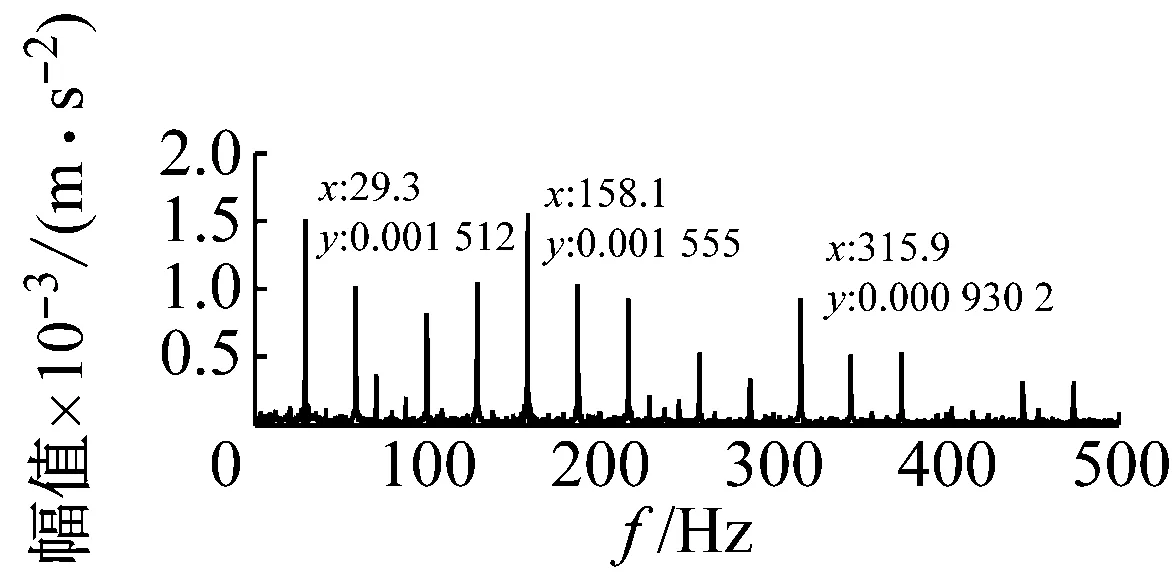
(d) 模型仿真信号频谱图
图8 缺陷尺寸为0.355 6 mm时的试验信号与模型仿真信号图
Fig.8 Signal spectrum of simulation and experiment under 0.355 6 mm defect size
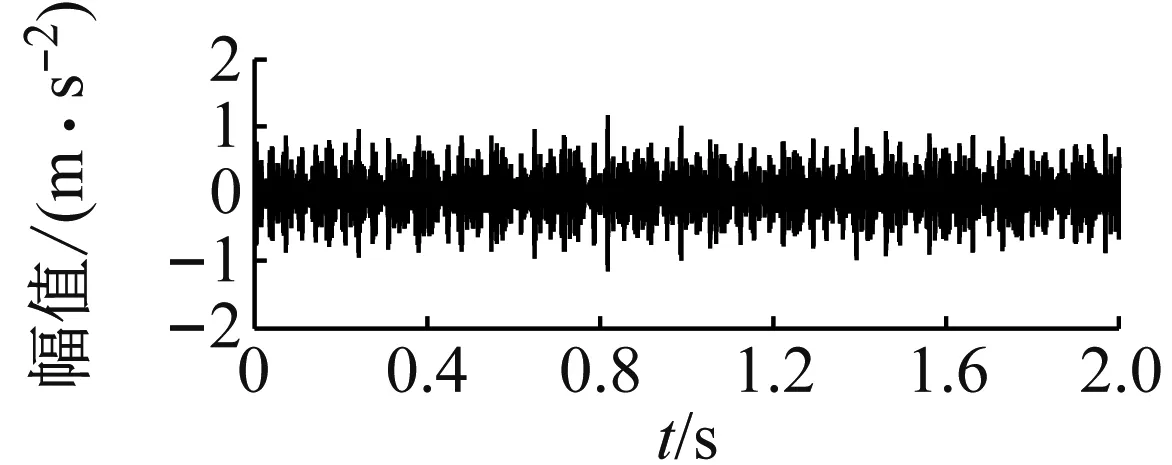
(a) 试验信号时域图
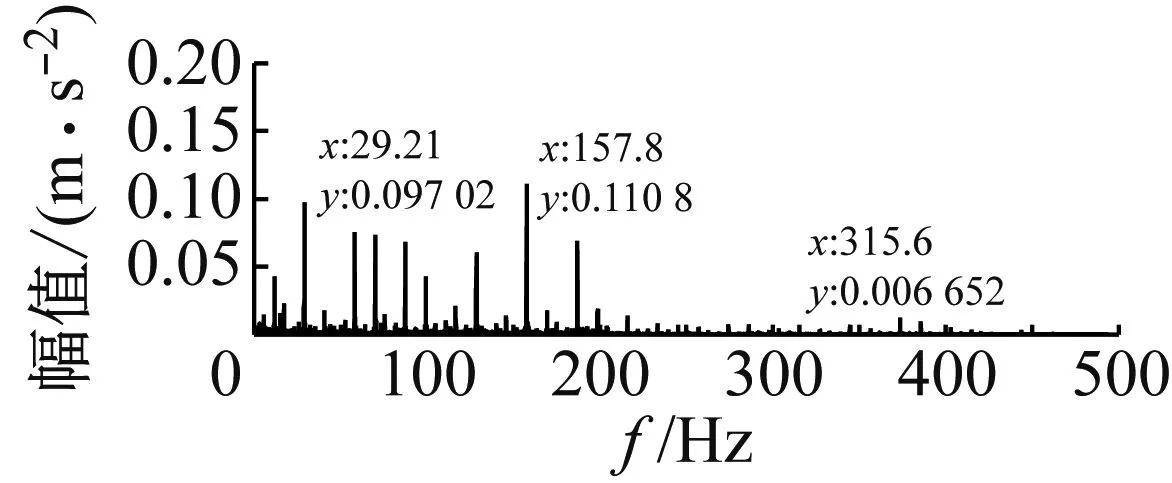
(b) 试验信号频谱图
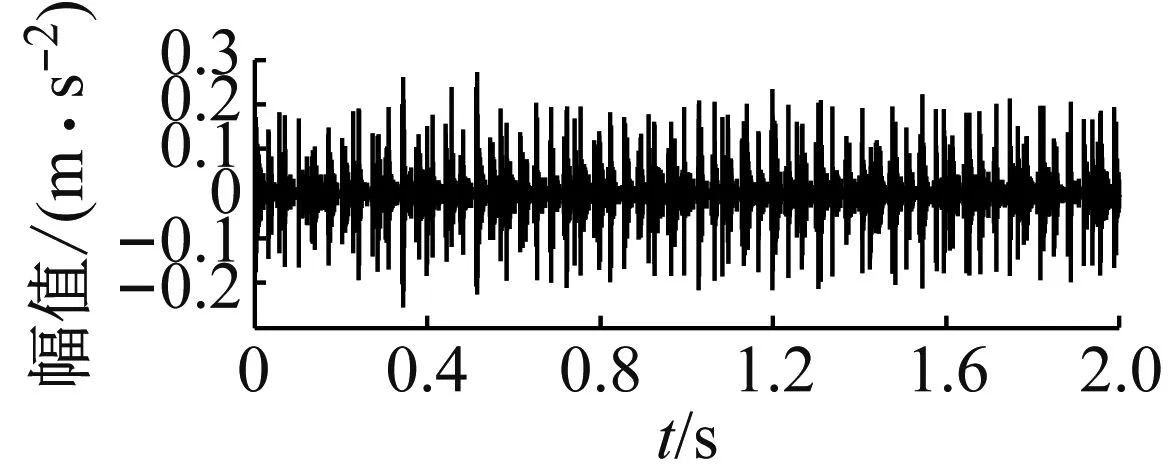
(c) 模型仿真信号时域图
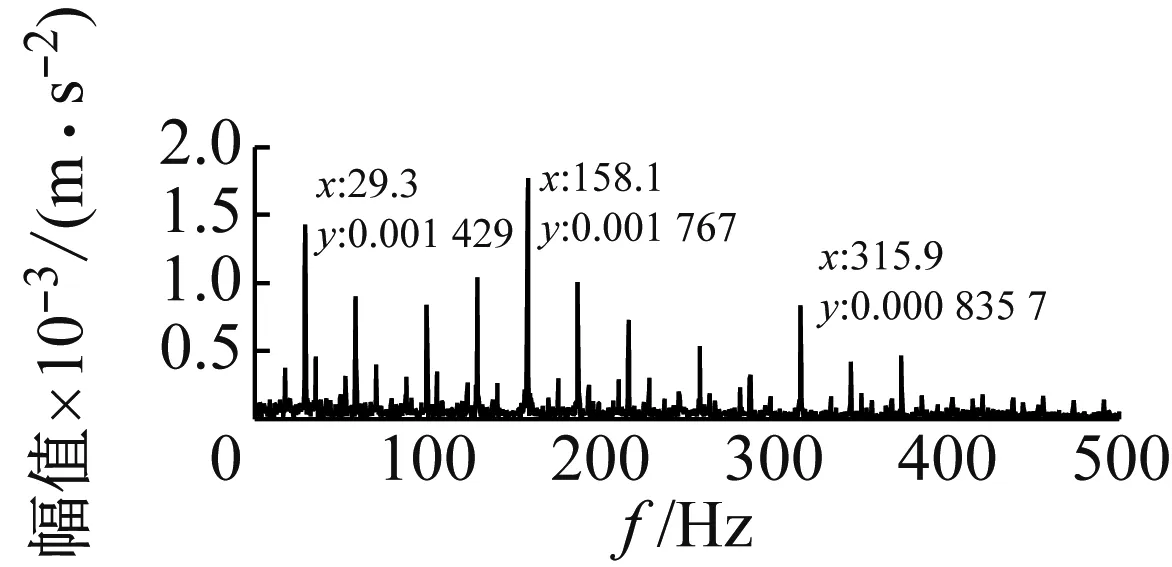
(d) 模型仿真信号频谱图
图9 缺陷尺寸为0.533 4 mm时的试验信号与模型仿真信号图
Fig.9 Signal spectrum of simulation and experiment under 0.533 4 mm defect size
通过对比不同缺陷尺寸下的试验信号图与模型仿真信号图(如图10所示),可以看出,随着测试轴承缺陷尺寸的增加,在试验信号图中,轴承内圈的转频,故障特征频率及其倍频的大小几乎不变,但它们所对应的加速度幅值基本上呈上升趋势。这是因为随着轴承缺陷尺寸的增大,引起了滚动轴承局部缺陷内部激励的增大,从而表现为振动响应幅值的增加。
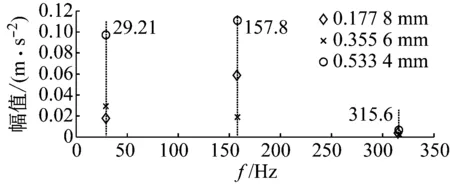
(a) 不同缺陷尺寸下试验信号的频率幅值图
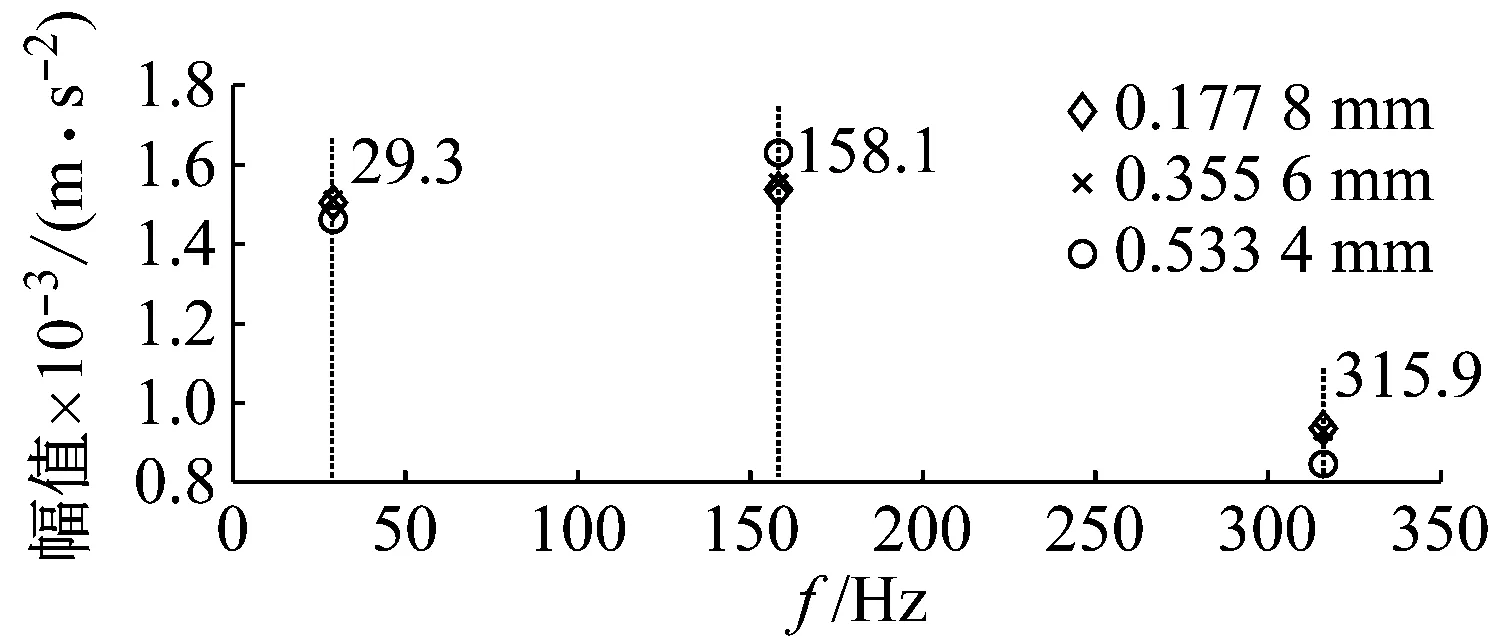
(b) 不同缺陷尺寸下模型仿真信号的频率幅值图图10 不同缺陷尺寸下的试验信号与模型仿真信号对比图Fig.10 Test signal and signal of model under different defect sizes
4.2.2 不同转速的影响
由于在时域上只能粗略地看到故障信号的冲击现象,而在频域上则能够详尽地分析振动信号的变化情况,因此在对不同转速对振动响应的影响的研究中,只考虑振动信号在频域上的表现。图11~图13分别为缺陷尺寸为0.533 4 mm,主轴转速分别为1 730 r/min、1 772 r/min和1 797 r/min时的试验信号频谱图和模型仿真信号频谱图。
从图11、图9(b)与9(d)、图12和图13中可以看出,对于试验信号图,能够非常明显地观察到其转频和故障特征频率及其周围的边频带,但特征频率的倍频及其边频带并不是很清晰。表明轴承内圈表面存在局部缺陷时,其冲击信号随频率的增加呈衰减趋势且衰减较快。故障特征频率的边频带主要由转频及转频倍频的调制产生,越靠近故障特征频率,边频的幅值越高,但特征频率的主频幅值始终高于其边频带的幅值。对于模型仿真信号图,如图11(b)、9(d)、12(b)和13(b)所示,可以清晰地观察到转频、特征缺陷频率及其二倍频和围绕在它们周围的边频带,且特征频率的幅值明显高于其周围边频带的幅值。相较试验信号频域图(图11(a)、9(b)、12(a)和13(a))而言,特征缺陷频率周围的边频带的分布更具有规律性,即边频带相对特征缺陷频率及其二倍频基本对称,且越靠近故障特征频率及其二倍频,边频的幅值越高。这可能是由于在低速情况下仿真信号比较稳定,相比真实试验环境并没有噪声成分的干扰,因此得到的谱图更加理想。
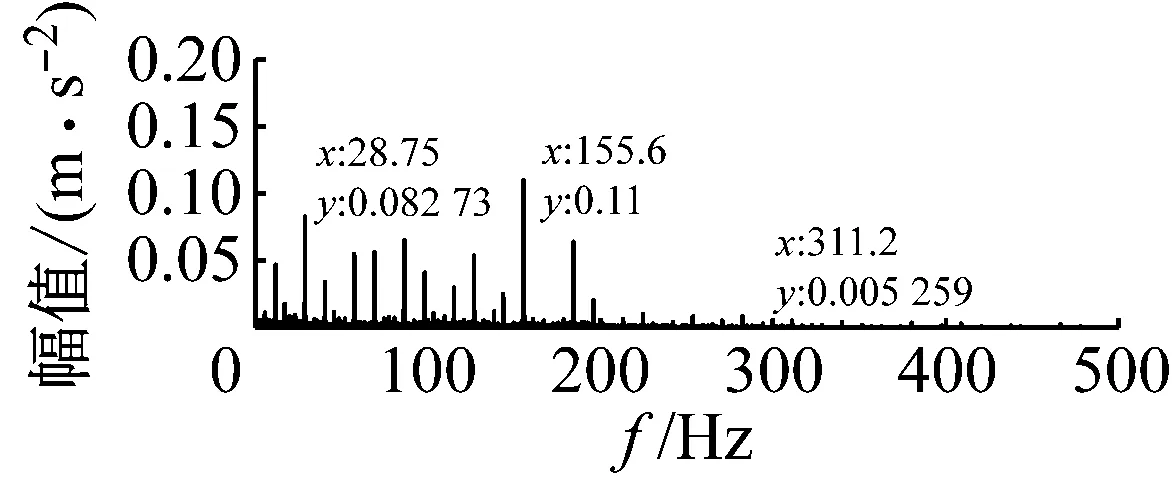
(a) 试验信号频谱图

(b) 模型仿真信号频谱图
图11 转速为1 730 r/min时的试验信号与模型仿真信号图
Fig.11 Signal spectrum of simulation and experiment under 1 730 r/min shaft rotational speed
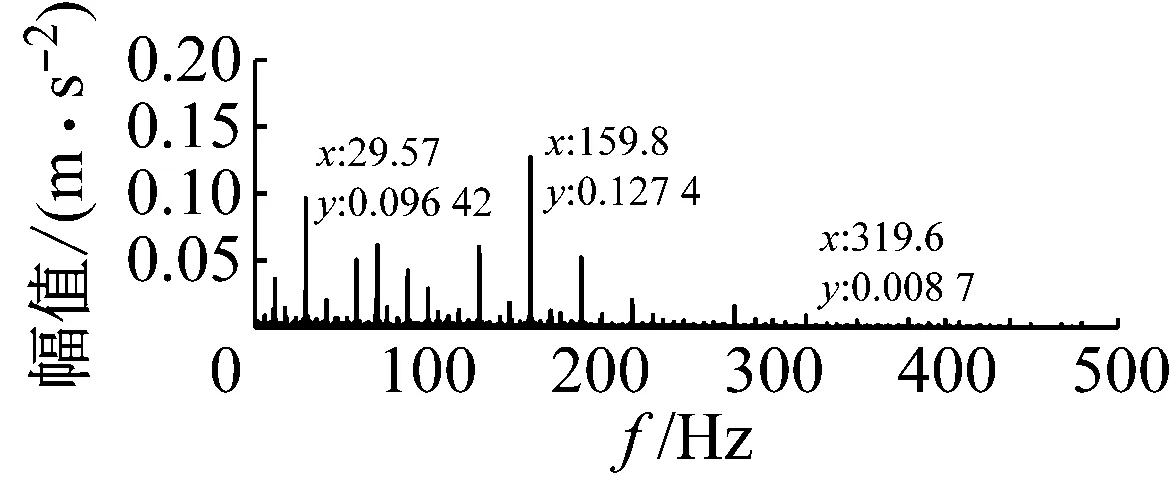
(a) 试验信号频谱图
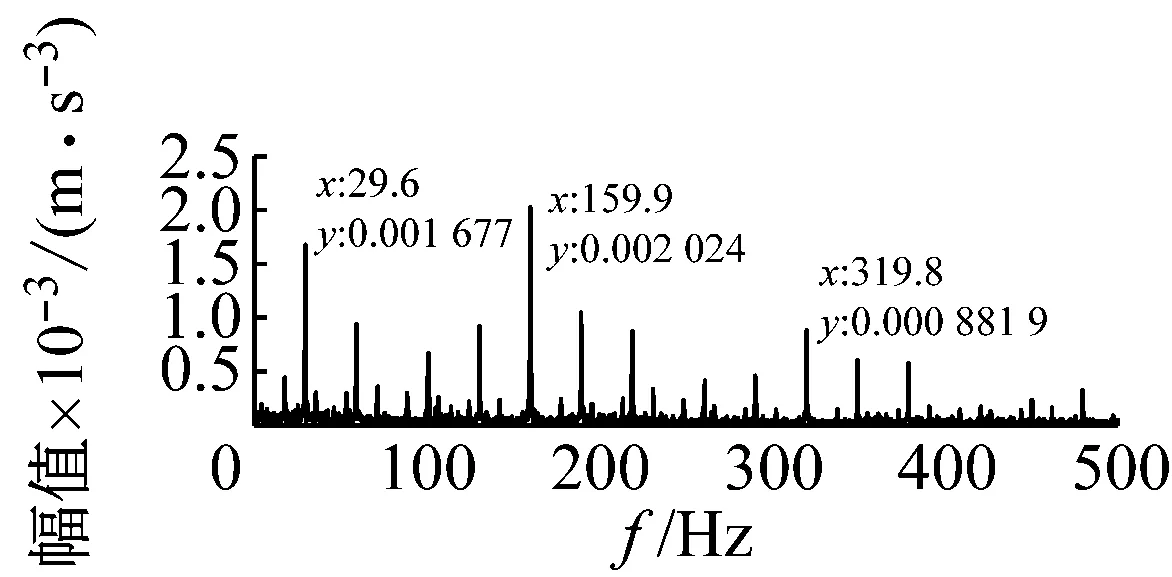
(b) 模型仿真信号频谱图
图12 转速为1 772 r/min时的试验信号与模型仿真信号图
Fig.12 Signal spectrum of simulation and experiment under 1 772 r/min shaft rotational speed
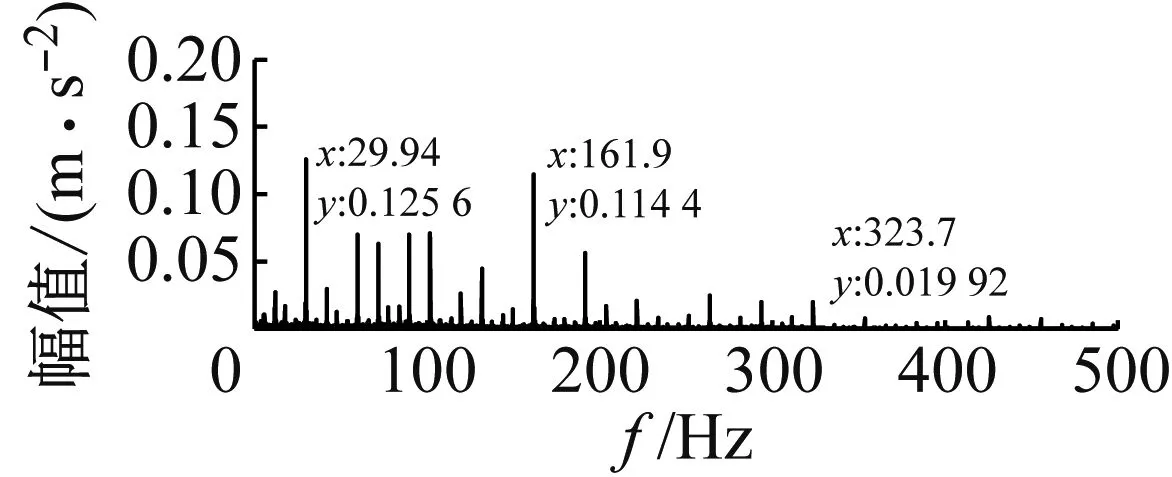
(a) 试验信号频谱图
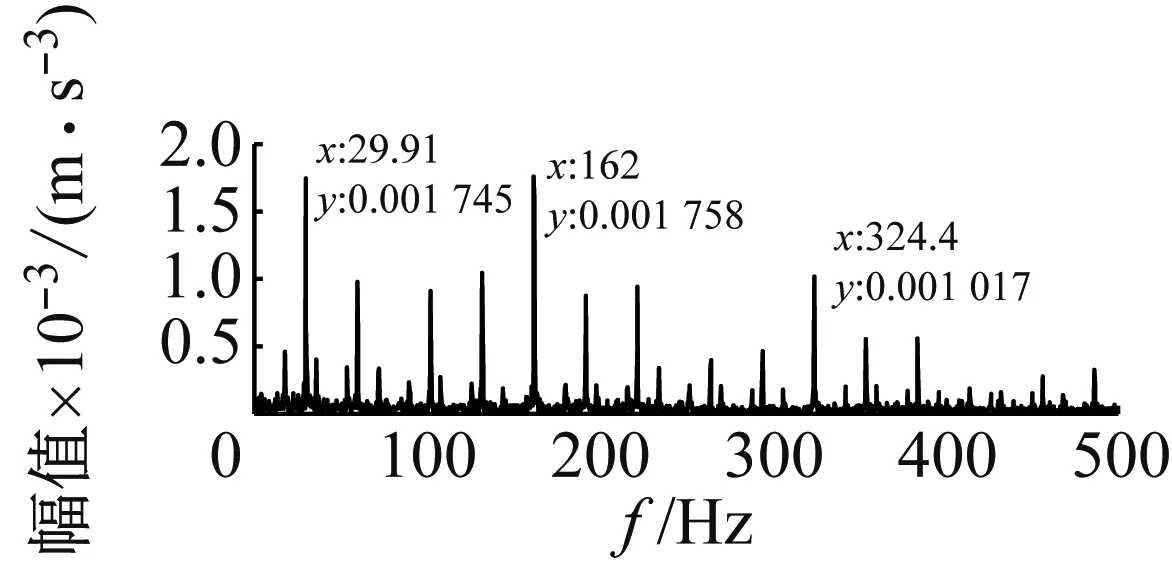
(b) 模型仿真信号频谱图
图13 转速为1 797 r/min时的试验信号与模型仿真信号图
Fig.13 Signal spectrum of simulation and experiment under 1 797 r/min shaft rotational speed
对比分析频域上试验信号图与模型仿真信号图,得到结果如图14所示。可以看出,随着测试轴承转速的增加,轴承内圈的转频,故障特征频率及其倍频的大小也随之增加,其对应的加速度幅值也发生了变化,且基本呈上升趋势。模型所仿真的加速度信号在转频、故障特征频率及其倍频以及加速度幅值的变化趋势与试验信号基本一致。试验信号图与模型仿真信号图的加速度幅值相差较大,可能是由于对试验数据的降噪处理不够彻底,也有可能是因为模型考虑因素不全,忽略其它因素所引起的。
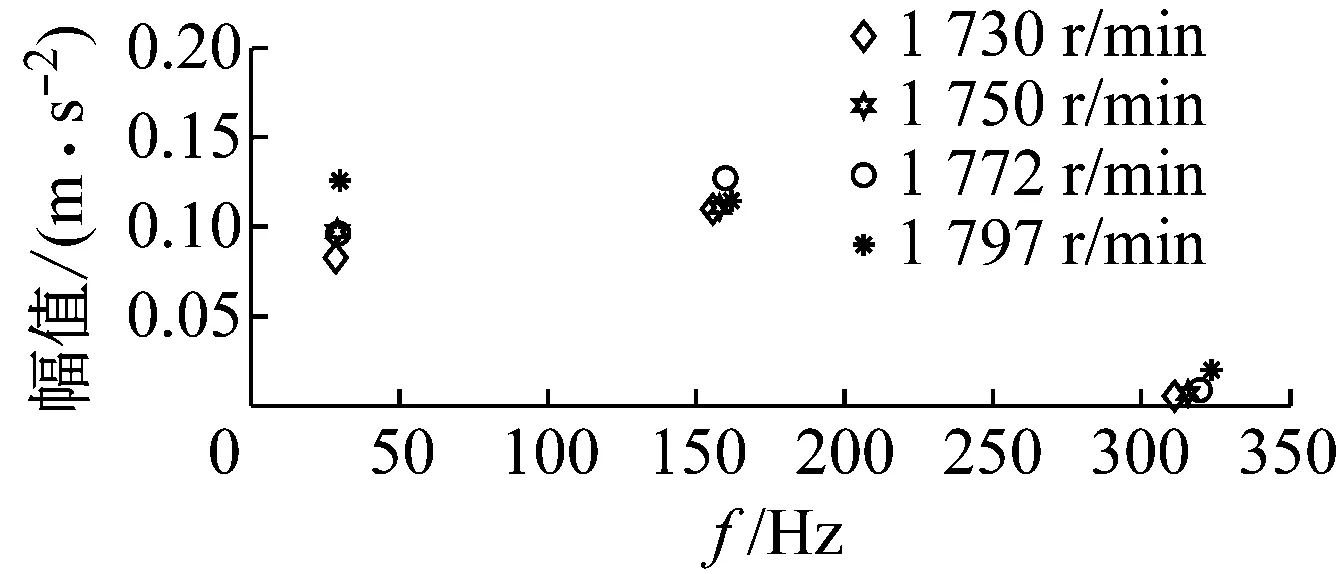
(a) 不同转速下试验信号的频率幅值图

(b) 不同转速下模型仿真信号的频率幅值图图14 不同转速下的试验信号与模型仿真信号对比图Fig.14 Test signal and signal of model under different shaft rotational speeds
4.2.3 缺陷尺寸、转速的影响规律
通过对模型在不同缺陷尺寸、不同转速下的动力学响应与实验测试结果的对比分析发现,所建模型的仿真结果与实验测试的振动响应变化情况基本一致。因此,在转速、缺陷尺寸变化较大的范围内研究轴承缺陷的振动响应,既能探究振动响应的变化趋势,又能够检验模型的强健性(某个或多个参数改变引起模型结果的改变情况)。图15和图16分别为缺陷尺寸和转速的变化对轴承系统振动响应的影响情况。
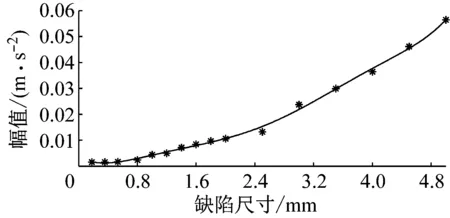
图15 缺陷尺寸对振动响应的影响趋势图Fig.15 Vibration response trendof effect of defect sizes
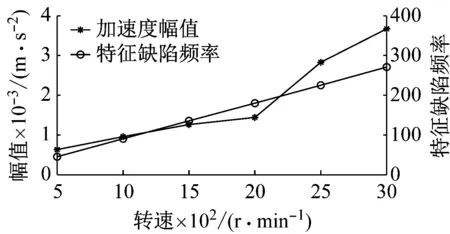
图16 转速对振动响应的影响趋势图Fig.16 Vibration response trend of effect of shaft rotational speeds
从图15可以看出,随着缺陷尺寸的增加,滚动轴承系统的振动加速度幅值在变大。当缺陷尺寸较小时,振动幅值的增加比较平缓;而当缺陷尺寸增大到一定程度时,振动幅值就会急剧增加。
从图16可以看出,随着主轴转速的增加,滚动轴承系统的振动加速度幅值也随之增大。当主轴转速较小时,振动幅值的增加比较平缓;而当主轴转速增大到一定程度时,振动就会加剧。而且,主轴转速对缺陷轴承的特征缺陷频率的大小也有显著影响,原因是主轴转速的变化直接影响了轴承转频的变化,进而影响了缺陷轴承的特征缺陷频率及其倍频和它们周围的边频带的数值大小。
综上所述,主轴转速的增大会使得轴承系统转频、特征缺陷频率及其倍频的大小同时增大;而且,主轴转速和缺陷尺寸的增加,都会引起特征缺陷频率处幅值的增大,加剧轴承的冲击振动,从而破坏了轴承系统正常运行,缩短了轴承的服役寿命。
5 结 论
(1) 考虑了多事件和时变位移,建立了一个滚动轴承局部缺陷动力学模型。研究了滚动轴承局部缺陷对系统动力学振动响应的影响。
(2) 模型假设缺陷形貌边缘为圆弧状,将滚动体经由缺陷的过程细化为多事件,构造了考虑轴承载荷-位移关系和缺陷引起的激励力变化关系的系统激励力函数。
(3) 通过所建模型,研究了不同转速和不同缺陷尺寸下的动力学响应规律。结果表明,高转速和大尺寸缺陷都会使振动幅值明显变大,进而加速轴承的失效。
(4) 通过对比模型仿真结果与实验测试结果,结果吻合度较好,说明所建模型的正确性和可行性。
