基于频域法的星箭连接分离装置的冲击载荷识别
2018-09-27张玉良岳洪浩邓宗全
张玉良, 杨 飞, 岳洪浩, 邓宗全, 徐 洋
(1. 哈尔滨工业大学 机电工程学院,哈尔滨 150001; 2. 东华大学 机电工程学院,上海 201620)
星箭连接分离装置位于卫星发射的关键部位,其稳定性对卫星的成功发射至关重要。星箭连接分离装置分离前需保持连接的绝对可靠,分离时必须迅速准确的分离,其过程会产生比较大的冲击载荷,火工分离装置分离过程中产生的加速度冲击甚至能达2 500g[1]。而其冲击载荷很大又难以直接测量,因此找到一种合适的星箭连接分离装置载荷识别方法,对其优化设计及稳定性分析都很有帮助,具有重要意义。
冲击载荷识别是动力学分析的逆问题,动载荷识别方法主要分为时域法和频域法两种[2]。时域法是在时域内,利用阶跃力积分来进行动载荷识别;而频域法主要利用测点响应和频响函数求逆来识别载荷,优点是直观、原理简单且便于应用。张礼才等[3]基于频域法,揭示了连采机井下采煤时受到的随机载荷内在的统计规律,并编制了连采机载荷谱;聂君锋等[4]也基于动态载荷的频域识别方法,对引射筒所受发动机试车产生的动态载荷进行了识别。考虑到工程实际中测点响应和频响函数相对容易获取,本文选取频域法对星箭连接分离装置进行冲击载荷识别。由于测点冲击响应中的干扰和噪声对频域法识别的准确性影响较大,可对测点冲击响应进行去噪重组。鉴于经验模态分解法(Empirical Mode Decomposition, EMD)在故障诊断[5]、冲击响应信号提取[6]中的成功应用,基于EEMD原理,对测点冲击响应EEMD分解,提取冲击响应部分,再进行冲击载荷识别,并对比去噪前后冲击载荷识别效果。
1 记忆合金型星箭连接分离机构
本文以一种基于记忆合金(Shape Memory Alloy, SMA)驱动的大承载低冲击连接分离装置[7]为研究对象,如图1所示,该连接分离装置的工作原理是:
(1)分离装置连接与锁紧:对承力螺杆施加预紧力,使承力螺杆产生弹性势能,并将预紧载荷传递至主传力螺母,使其产生转动势能,锁紧载荷进一步传递至两级摆臂,根据力矩平衡原理,锁紧载荷逐级减小。此时触发转轴对一级摆臂进行限位,一级摆臂对二级摆臂进行限位,二级摆臂又对主传力螺母进行限位,以保持主传力螺母的转动势能。
(2)分离装置解锁与分离:当SMA驱动接收到上级供电后,电能转变为热能,由于SMA具有应变储能特性,当达到SMA相变温度时,SMA产生回复应力和应变,带动触发轴转动,解除对一级摆臂限位,一级摆臂释放撞击1号点,继而二级摆臂限位解除撞击2号点,从而解除主承力螺母为非自锁梯形螺纹连接,主承力螺母转动势能释放并转变为承力螺杆直线运动动能,承力螺杆最终脱离连接界面,星箭实现解锁分离。
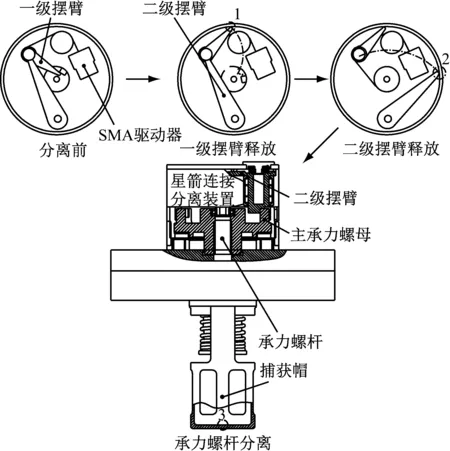
图1 星箭连接分离装置及分离过程示意图Fig.1 The Fig of connection separation device of satellite and rocket and separation process
通过以上分析,该装置分离过程中会产生三次冲击载荷,如何识别这三次冲击载荷大小即为本文主要研究内容。
2 基于EEMD去噪的星箭解锁分离机构冲击载荷识别方法研究
2.1 频域法的冲击载荷识别原理
动载荷识别的频域法识别主要为两类,即模态坐标变换法和频响函数矩阵求逆法。模态坐标变换法是在模态参数均已知的情况下,基于模态坐标系来求解未知动载荷,但在工程实际中,模态参数难以确定。而频响函数矩阵求逆法只需要知道频响函数矩阵和测点响应谱矩阵,便能求出载荷谱,这在工程实际中比较容易实现。基于已有实验条件,本文基于频响函数矩阵求逆法,对星箭连接分离装置分离过程产生的冲击载荷进行识别。
2.2 频响函数矩阵求逆法
对于确定性响应,设需要识别载荷数为nf、测得的响应数为nu、线性结构的动载荷阵列[F(ω)nf×1]、测得响应阵列为[U(ω)nu×1],他们满足如下关系
[U(ω)nu×1]=[H(ω)nu×nf][F(ω)nf×1]
(1)
式中:[H(ω)nu×nf]是系统的频响函数矩阵,故待求动载荷[F(ω)nf×1]可由以下公式求出
[F(ω)nf×1]=[H(ω)nu×nf]+[U(ω)nu×1]=
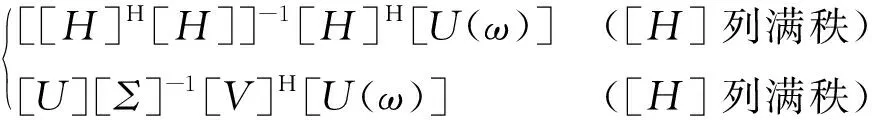
(2)
式中:角标“+”表示矩阵[H(ω)nu×nf]的Moore-Penrose伪逆,即广义逆;“H”表示矩阵的复共轭转置;[U]和[V]分别为两个酉矩阵;对角阵[Σ]=diag(σ1,σ2,…,σn),σ1≥σ2≥…≥σn≥0为变换矩阵所有的奇异值,当rank(H) 经验模态分解法(EMD)是由Huang[8]于1998年提出,EMD几乎能对所有非平稳信号进行平稳化处理,将非平稳信号按不同尺度逐级展开,分解成具有不同物理意义的本征模态函数IMF和表征信号整体变化趋势的残余分量。设原始信号为y(t),则对其进行EMD分解,最终可得到 (3) 由式(3)可以看出:原始信号y(t)可分解为一系列固有模态函数cn(t)和残余分量rn(t)。EMD已经被应用于很多领域,但仍存在一些待解决的问题,比较突出的是容易产生模态混叠,而EEMD则比较好地解决了这个问题。 EEMD算法的核心是EMD,但相对于EMD分解效果更好,比较好地解决了模态混叠的问题。EEMD的具体分解过程如图2所示,图2中最后结果ai便是EEMD分解原始信号y(t)得到的各阶模态分量IMFs。EMD及EEMD在冲击特征提取及去噪方面的应用研究有:张春棋等[9]对爆炸冲击信号进行EMD分解并结合时频分析,精确反应了爆炸冲击信号的特征;赵明生等[10]研究了EEMD在爆破振动信号去噪中的应用,发现EEMD去噪效果比较理想;刘连生等[11]采用小波阈值法、EMD以及EEMD的信号去噪方法分别对露天爆破开采下所获得的爆破地震波信号进行去噪处理,结果表明EEMD去噪效果最好。 图2 EEMD分解过程Fig.2 The decomposition process of EEMD 基于已有研究并结合EEMD,可考虑将星箭解锁分离机构分离时产生的原始冲击信号按高低频逐级分解开来[12],再去掉噪声、干扰和固有模态部分,提取冲击响应部分参与载荷识别。 该装置在解锁分离过程中会产生3次冲击,由于激励点数及位置均已知,且3次激励之间有细微时间间隔,也可以看作是单点不同位置的激励。基于频响函数矩阵求逆法,只要再测出该装置的频响函数以及不同测点的响应即可求出3次冲击载荷的大小。在以上分析的基础上,选取合适的点对该装置进行简化如图3所示,数字标号为对应节点号,装置解锁分离时产生的冲击部位依次为1,2,25。 图3 星箭连接分离装置简化线框模型及测点布置Fig.3 The simplified wireframe model and measuring point arrangement of connection separation device 载荷识别研究是建立在系统实测响应基础上,结构响应的测量是重要环节之一。测点数目取决于所选频率范围、期望模态数、试件上所关心区域及现有传感器数目等多项因素。当测点位置选择不合适或者测点数量太少,会使结构上部分重要位置的运动丢失。根据测点布置原则及试验要求,为获取频响函数,在星箭解锁分离机构的壳体,捕获帽以及连接的蜂窝板上均匀布点,尤其是在各部件之间关节连接处也相应布点。测点分布如图3所示,在充分考虑各载荷分量作用情况下,选择合适的响应测量点,从C1-C22共22个测点,C15、C16、C19-C22这6个测点布置三轴加速度传感器测量XYZ三个方向,其它16个测点布置单向加速度传感器测量法向,坐标系设定为图3中左下角所示,实物传感器布置如图4所示。 图4 星箭连接分离装置实物测点布置Fig.4 The measuring point arrangement of connection separation device of satellite and rocket 节点号1、节点号2分别对应摆臂一和摆臂二释放的冲击点,节点号25为第三次冲击载荷作用点,在分离前先在装置上敲击冲击点,测量各测点响应,分别估算出节点号1、节点号2、节点号25与各测点之间的频响函数曲线。星箭分离时,同时用压电式加速度传感器、本次测量采用东华测试软件公司的DH5922数据采集系统进行数据采集及频响函数的分析。 对于简化模型(图3),在星箭连接分离装置分离器前,先分别测量并得到1,2,25点和其它各点之间的频响函数,星箭分离装置解锁分离过程中再测得各点的冲击响应信号,各点响应为1,2,25三点冲击载荷激励引起。1,2,25三点处冲击响应为 [U(ω)nu×1]=[H(ω)nu×nf][F(ω)nf×1] (4) 展开为(n为响应测点数) (5) 根据测点布置可知n=22,i为星箭分离装置的冲击载荷作用点,分别对应1,2,25这三个点,设i=1,2,25,则其冲击载荷可以表示为Fi(ω) (6) 再对F1(ω)、F2(ω)、F25(ω)进行傅里叶逆变换,可得冲击载荷的时间历程如下 f1(t)=FFT-1[F1(ω)] (7) f2(t)=FFT-1[F2(ω)] (8) f25(t)=FFT-1[F25(ω)] (9) 在以上方法载荷识别过程中,有时会遇到结构矩阵求逆是病态的,一般采用最小二乘正则化算法[13],以解决载荷识别求解过程中遇到的病态问题。 试验模态分析方法包含多种方法,本文采用测力法中的锤击单点激励法,再结合频响函数理论取得激励点和测点之间的频响函数。设备连接如图5所示,三向加速度传感器位置即为测点C1-C22(图3)。 图5 试验设备连接图Fig.5 Test equipment connection diagram 加速度传感器试验参数设置如表1所示。 表1 试验数据采集主要参数设置Tab.1 The main parameter setting of test data acquisition 现以激励点1和测点C1为例,求其之间的频响函数。激励点1为脉冲激励,如图6所示,脉冲峰值为823 N,方向为+Y,数据采集时间0.41 s。在激励的同时,各测点加速度传感器也在测量各位置的激励响应,测点C1测得对应脉冲响应如图7所示,方向为+X。 通过激励点1、测点C1采集的数据及频响函数理论,可以得到激励点1和测点C1之间的频响函数如图8所示。同理,通过以上方法可以得到激励点1和各测点的频响函数,如图9所示。也可以获得激励点2、25分别和其它测点的频响函数。 图6 激励点1脉冲激励Fig.6 The pulse excitation of excitation point 1 图7 测点C1脉冲响应Fig.7 The impulse response of the excitation point C1 图8 测点C1对应激励点1频响函数Fig.8 The frequency response function between the excitation point C1 and the excitation point 1 图9 激励点1与各测点频响函数(部分显示)Fig.9 The frequency response function between the excitation point 1 and the other excitation points 为了验证测点C1的响应是否由激励点1引起,下面再分析他们之间的相关性。由于相干函数可以检验信号的置信度,因此输入与输出间的相关性可用相干函数来分析。相干函数值越小,说明输入与输出之间相干程度也越小;反之,相干函数值越接近1,说明输入与输出的相干程度也就越大。本试验激励点1与测点C1之间的相干函数如图10所示,从图中分析可知,其函数值在频率小于3 000 Hz部分都十分接近1,所以得到的频响函数具有较高的可信度。 图10 测点C1与激励点1间的相干函数Fig.10 The coherence function between C1 and excitation point 1 获得频响函数后,结合式(6)及载荷识别模型可知,只需要再知道该装置分离过程各测点的冲击响应(图11),便可求得冲击载荷大小。 图11 各测点冲击响应Fig.11 The shock response signal of all excitation points 借助于MATLAB计算,可以求得Fi(ω),再对Fi(ω)进行傅里叶逆变换,即 f(t)=FFT-1[F(ω)] (10) 可以求得冲击载荷的时间历程如图12所示。 根据频响函数矩阵求逆法的冲击载荷识别结果可知,此方法能够较准确得到冲击载荷的大小,同时也可以看到识别的精度不是很高,包含有大量噪声和干扰引起的非冲击载荷部分。下面再基于EEMD原理,将各测点冲击响应信号去噪处理后,再进行载荷识别。 对测点C1的冲击响应信号进行EEMD分解,如图13所示,图中第一个信号为原始信号,后面依次为模态分量IMF1-IMF7,最后一个为分解后的余项RES,RES是一个幅值变化很小的序列,表征了测点C1处冲击响应的整体趋势。再对EEMD分解的模态分量做频谱分析分析,如图14即为测点C1处冲击响应信号的EEMD分解频谱图。 图12 冲击载荷识别结果Fig.12 The results of the impact load identification 图13 测点C1冲击响应的EEMD分解Fig.13 The EEMD decomposition of the excitation point 1 由EEMD分解结果可知,原始冲击信号中同时包含了高频成分和中低频成分,其中高频成分是由冲击所致,而中低频成分是冲击载荷激起的固有频率振动和局部振动。据此,单独提取出IMF1作为测点C1仅由冲击引起的响应部分,IMF1如图15所示,下面将去噪后提取的IMF1作为C1点冲击响应,再进行冲击载荷识别。由式(9)和式(10)可得EEMD去噪的冲击载荷识别结果如图16所示。由图中载荷识别结果可知,EEMD去噪后冲击载荷识别结果要明显优于去噪前的结果,识别结果中的噪声和干扰比较小。 图14 测点1冲击响应EEMD分解各IMF对应频谱图Fig.14 The spectrograms of the excitation point 1based on the denoising of EEMD 图15 测点C1 EEMD分解后的IMF1Fig.15 The IMF1 of the EEMD decomposition of the excitation point C1 图16 基于EEMD去噪识别的冲击载荷Fig.16 The results of the impact load identification based on the de-noising of EEMD 为比较频域法及基于EEMD去噪的后冲击载荷识别效果,设计出一个既能直接测量冲击载荷大小,又可测量各测点响应的实验方案,如图17所示。 J1,J2,J3是三次冲击点,在此处布置微型压电式测力传感器,用于直接测量三次冲击载荷;C1-C22是测点布置,按照图中的测点布置方案进行安装。本次试验分为两次数据采集:① 星箭连接分离装置分离前的锤击法测频响函数;② 星箭连接分离装置分离过程中的冲击载荷及各测点的冲击响应。测得实验数据后,由冲击载荷识别方法可以得到的结果如图18所示。 图17 实验方案图Fig.17 TheFig of experimental plan 图18 实验测得冲击载荷大小Fig.18 The measured impact load 根据图18,对于不同载荷识别方法和试验测量结果对比如表2所示。 表2 载荷识别方法结果对比Tab.2 Thecomparison of the results of the identification methods 对比以上载荷识别方法和实验结果可知:在识别精度上,基于EEMD去噪的频域法识别结果更接近于测量真实值,基于EEMD去噪识别的冲击载荷峰值和测量值相比在16 N以内,而不去噪的频域法识别结果在57 N以内;另外从脉冲宽度对比可知,频域法识别结果中含有比较多的干扰和噪声,造成识别的脉冲宽度过大,而基于EEMD去噪载荷识别结果法更为理想。 本文详细介绍了频响函数矩阵求逆法的载荷识别原理,并对星箭连接分离装置分离过程产生的3次冲击载荷进行识别。先选取频域法中的频响函数矩阵求逆法对该装置进行冲击载荷识别,再选取基于EEMD去噪的频域法进行计算对比。 由载荷识别结果及实验可知:基于EEMD去噪的频域法识别结果更优,其含有干扰及噪声成分更少;而普通频域法识别结果中掺杂有部分非冲击载荷部分。由此可知基于EEMD去噪的频域法冲击载荷识别效果要明显优于普通的频域法,该方法也可推广到火工分离装置、枪炮发射等冲击载荷较大,且不易测量的装置上,该方法对于装置优化设计及环境分析很有帮助。2.3 EEMD去噪原理
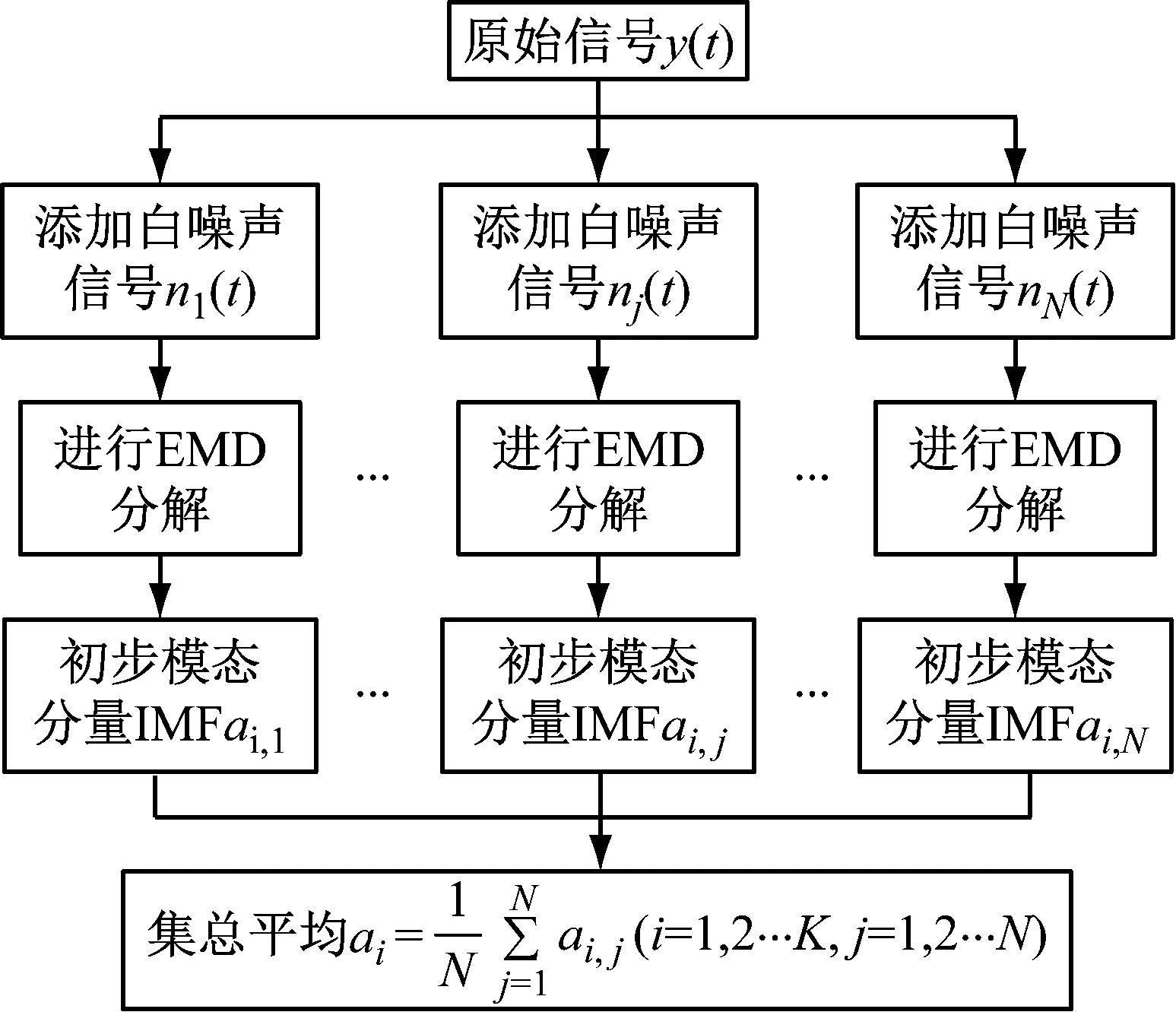
3 基于频域法的星箭连接分离装置冲击载荷识别方法研究
3.1 星箭连接分离装置冲击载荷识别模型的建立
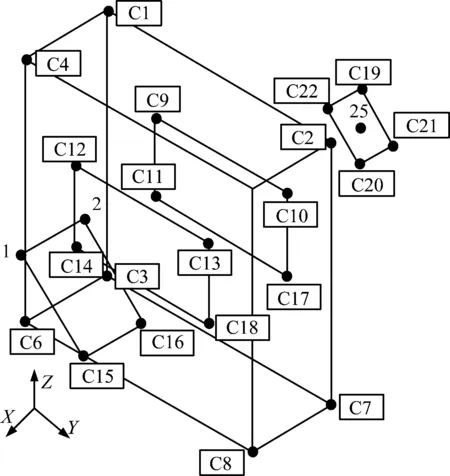

3.2 基于试验模态分析法的频响函数获取
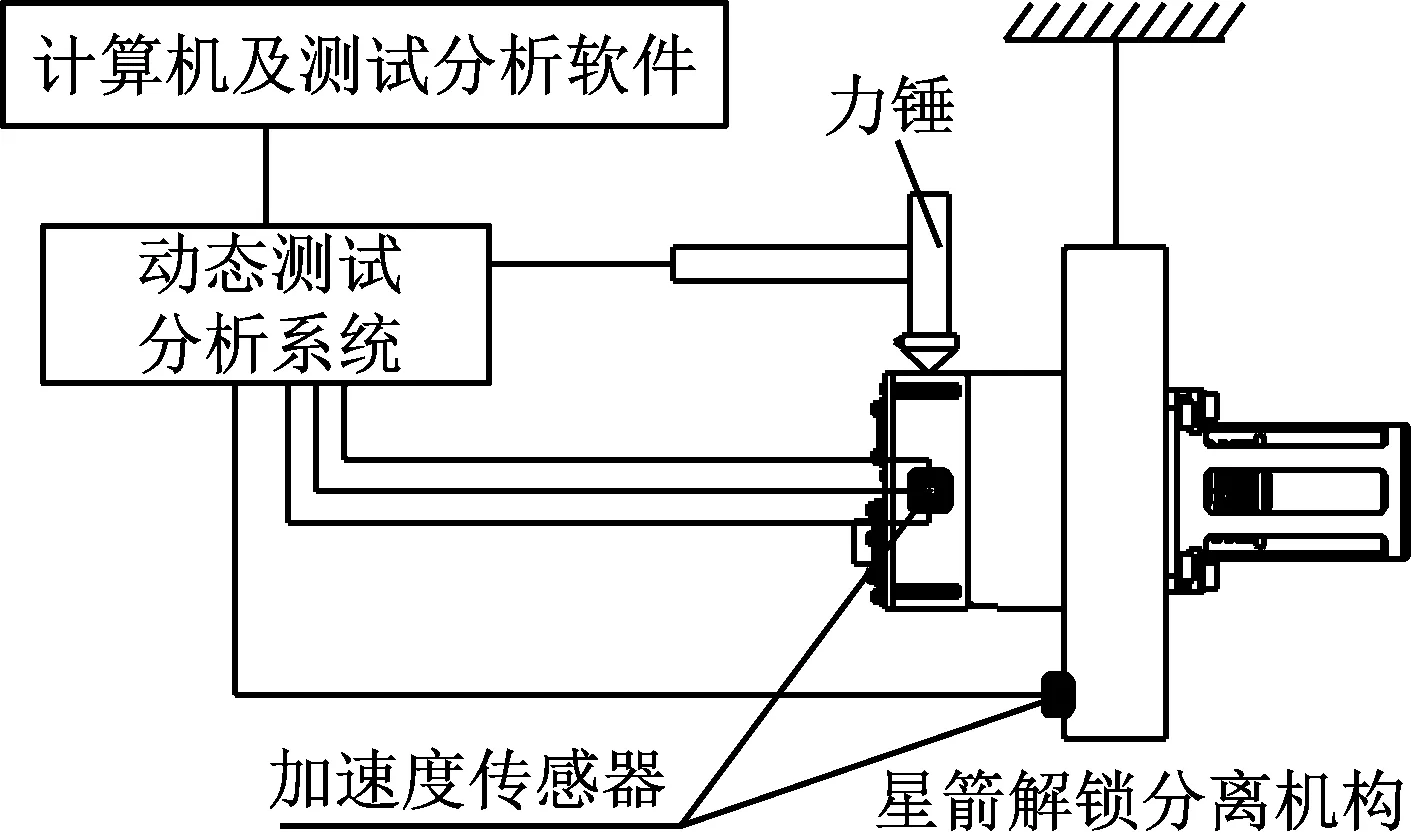

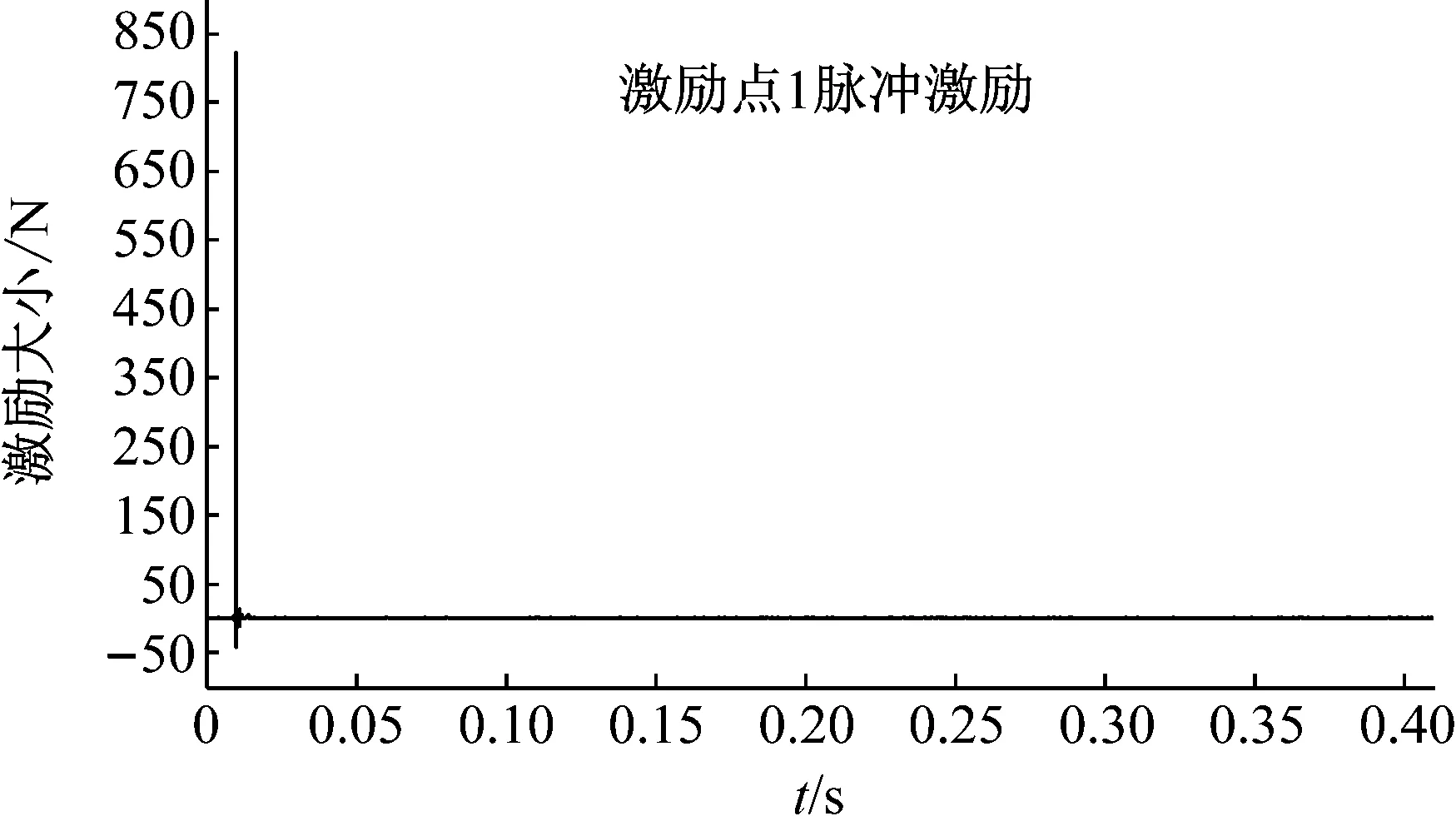
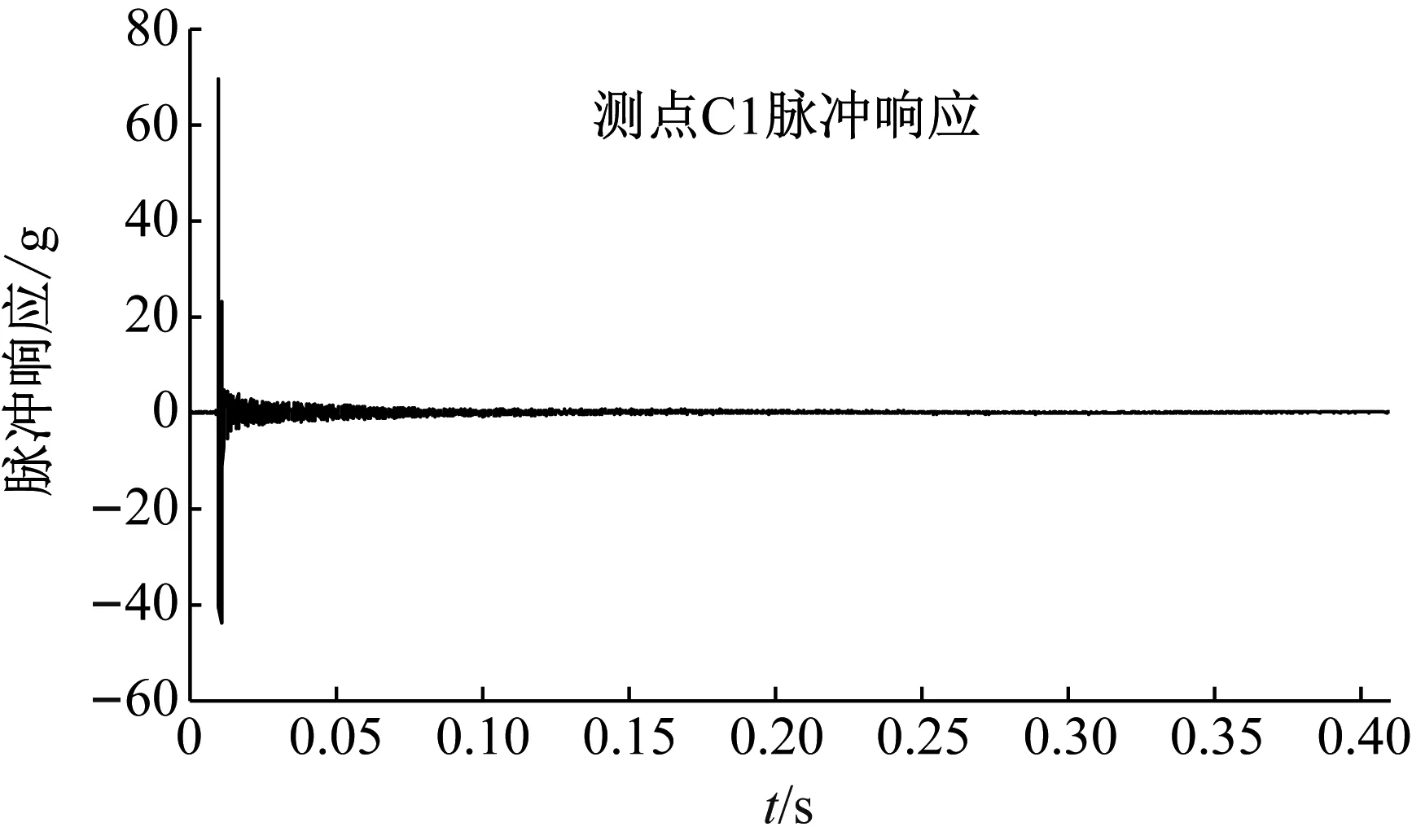
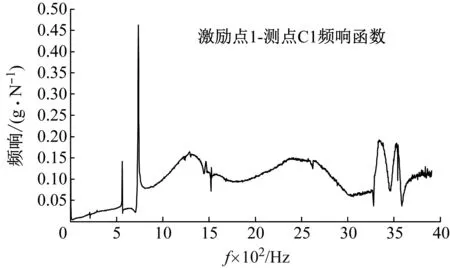
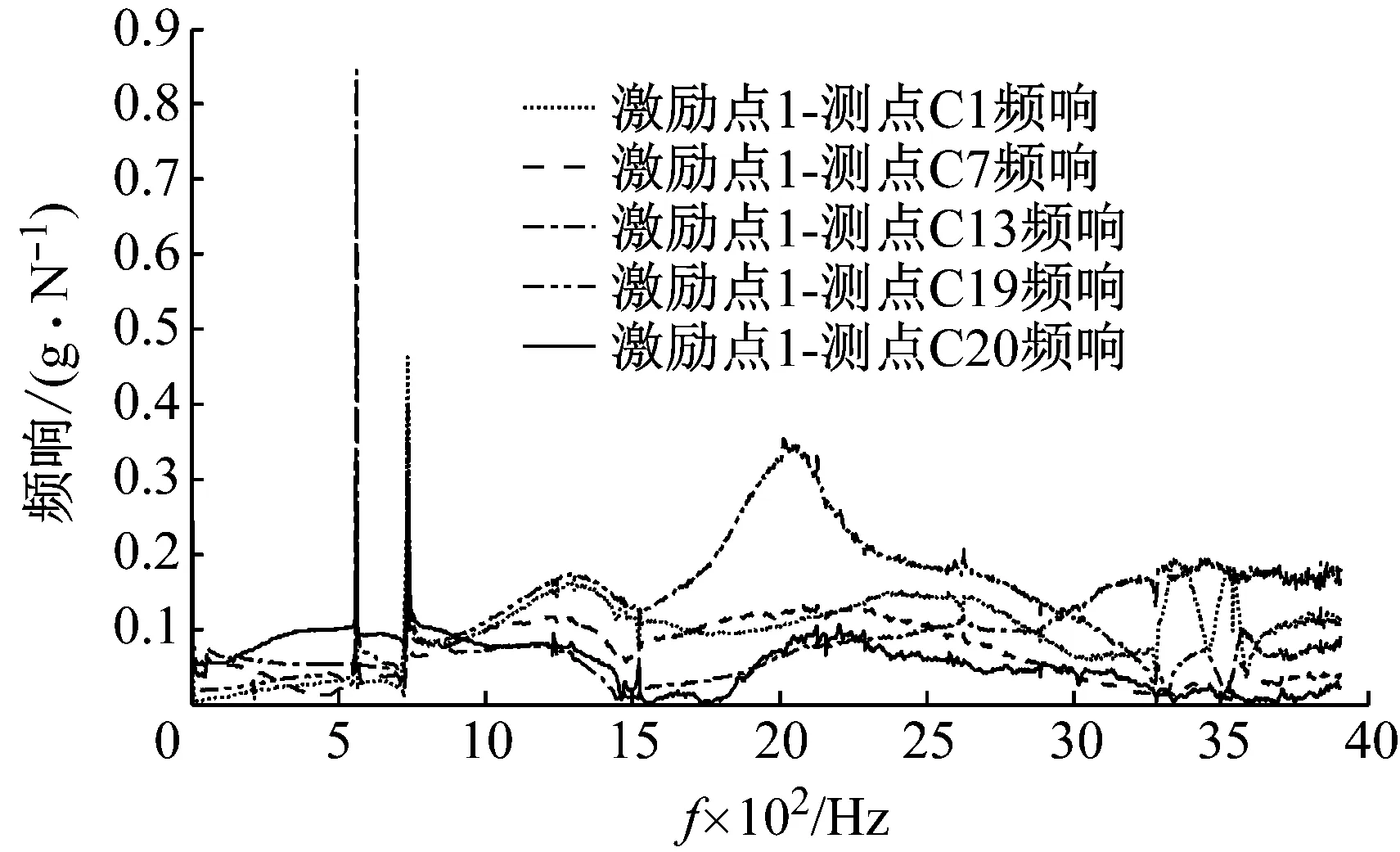
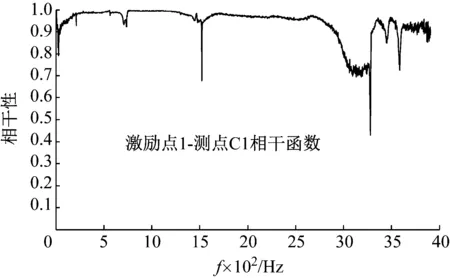
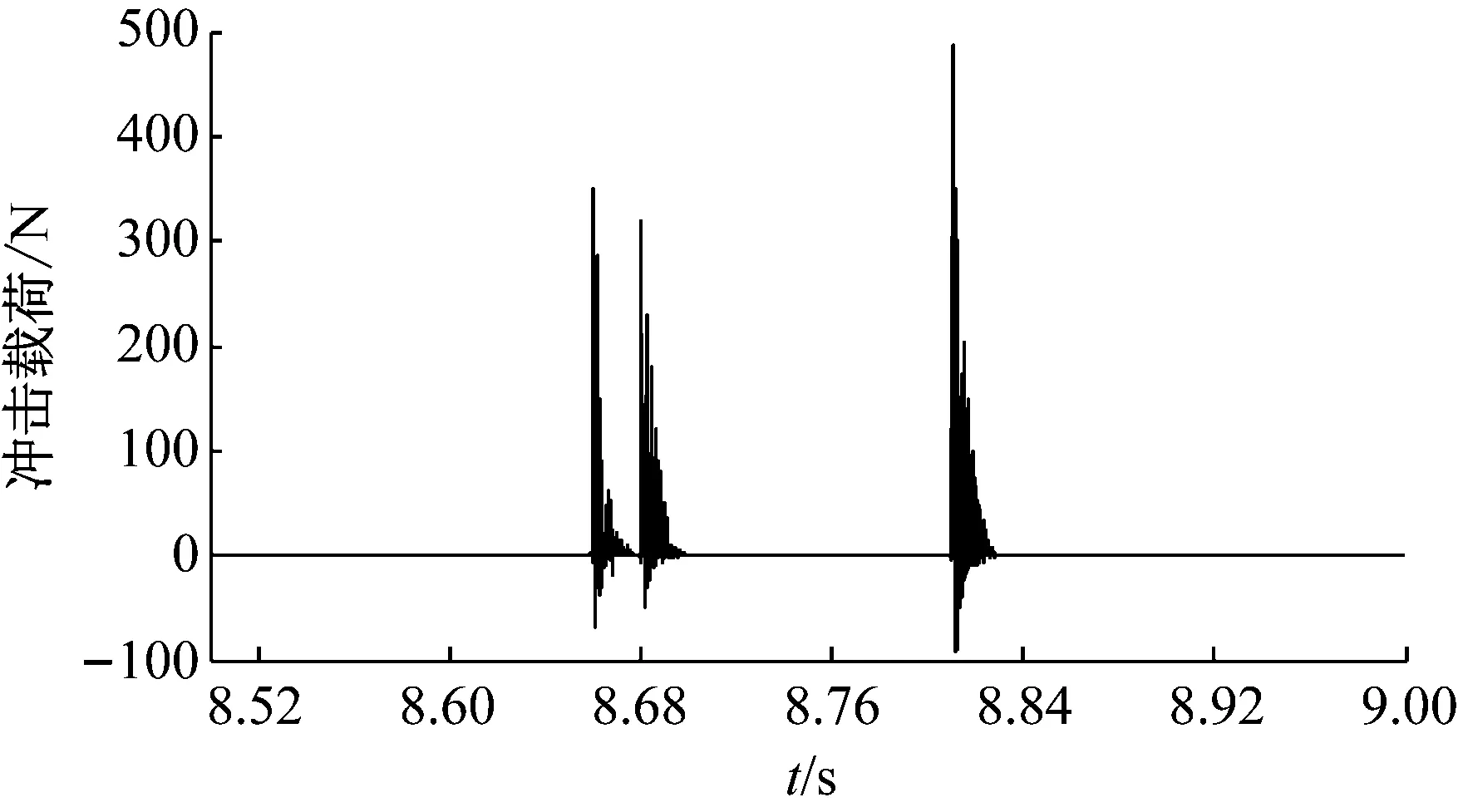
3.3 基于频响函数矩阵求逆法的载荷识别
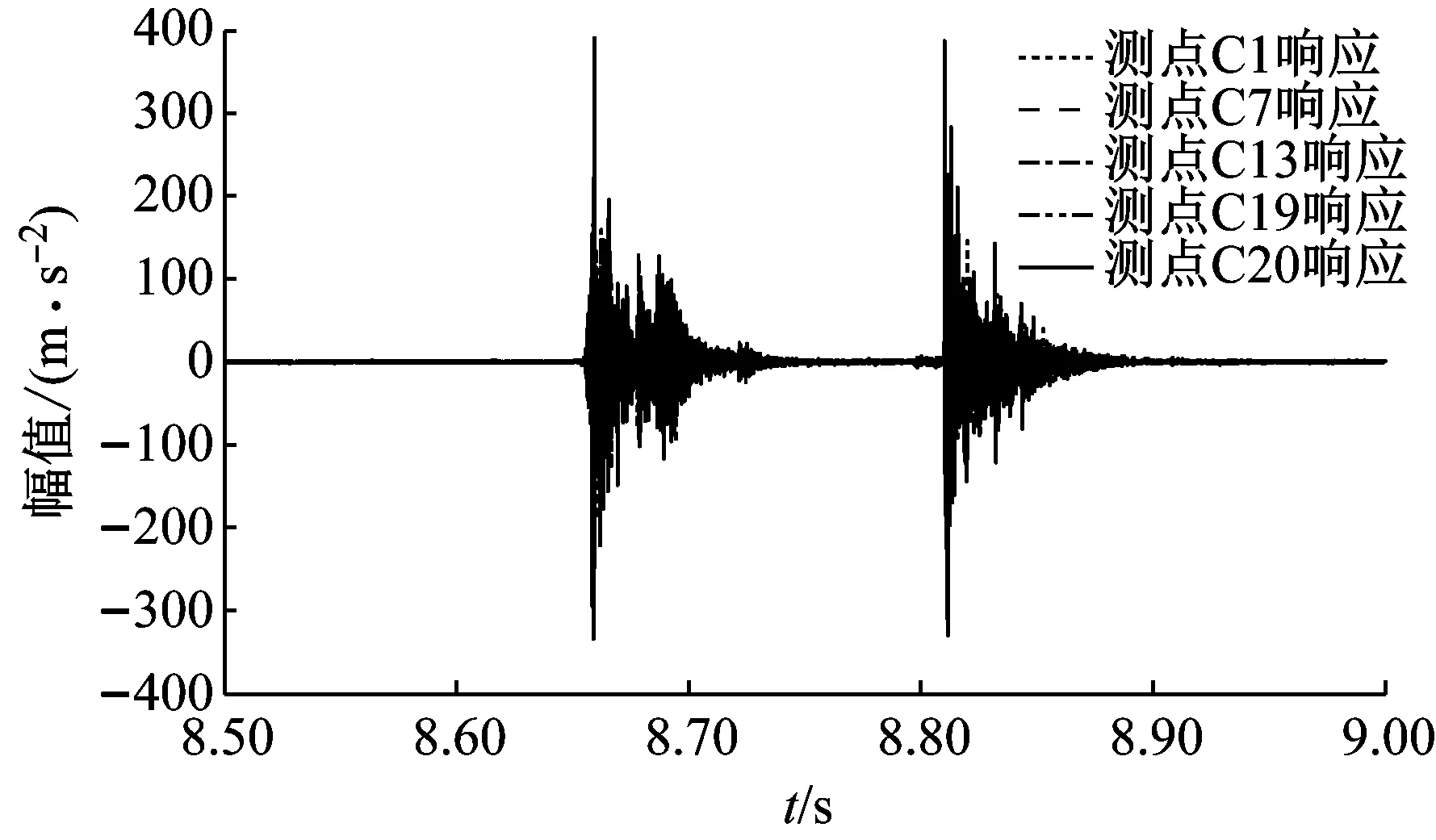
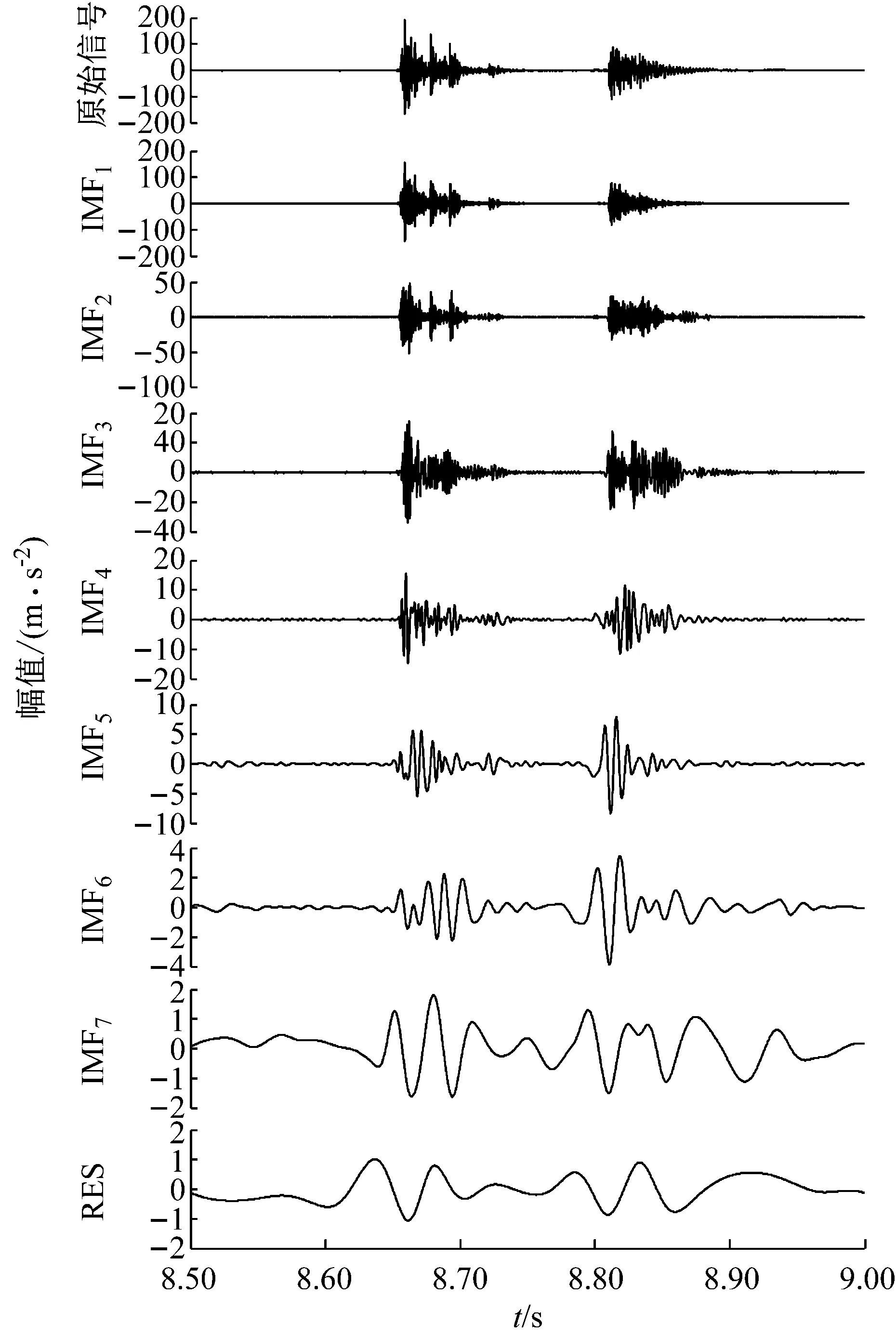
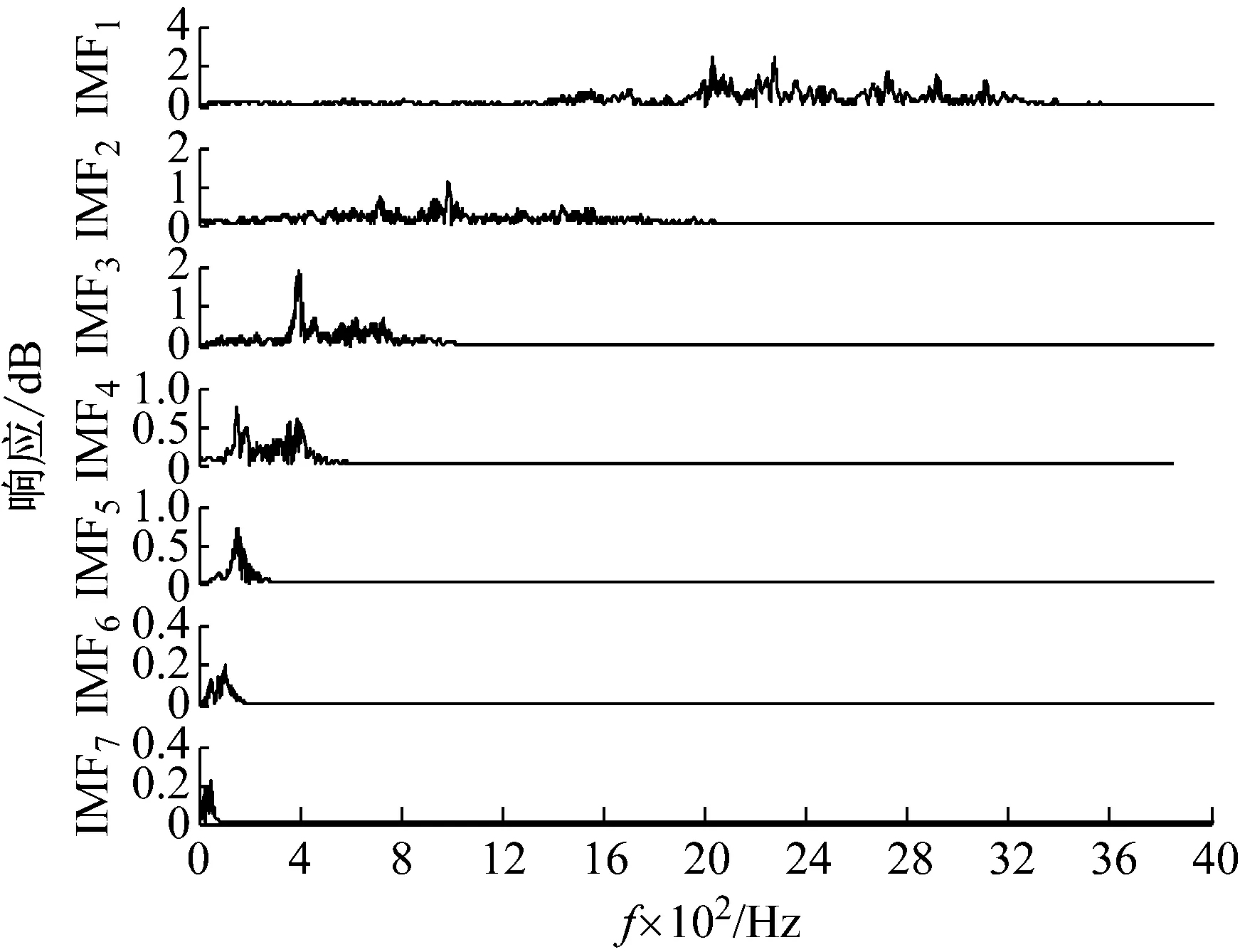
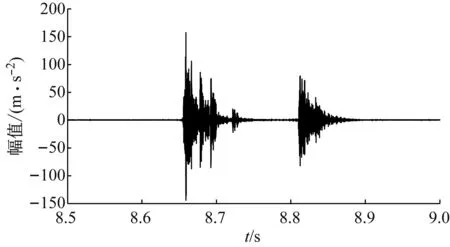
3.4 基于EEMD去噪的冲击载荷识别
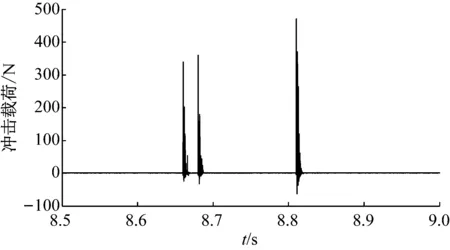
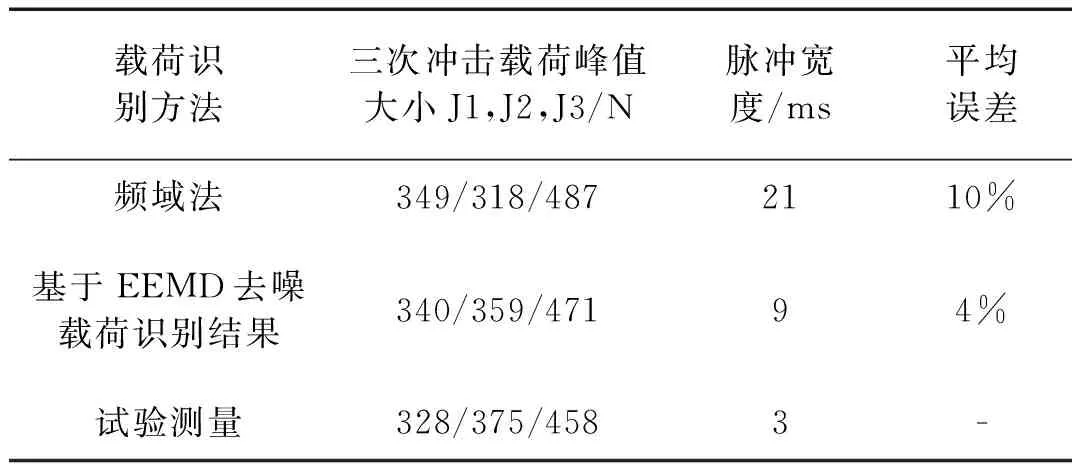
4 实验及结果分析


5 结 论
