液化天然气储罐混凝土穹顶的冲击破坏模式与机理*

2018-09-27翟希梅赵新宇

爆炸与冲击 2018年5期

翟希梅,赵新宇

(1.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，黑龙江哈尔滨 150090； 2.哈尔滨工业大学土木工程智能防灾减灾工业和信息化部重点实验室，黑龙江哈尔滨 150090)

近年来，对清洁能源的需求逐年激增，天然气(liquefied natural gas, LNG)由于绿色环保、经济实惠、安全可靠等优点逐渐成为21世纪最重要的能源，LNG储罐结构也得到更多的应用。由于有针对性的恐怖袭击事件频发，鉴于LNG储罐结构的重要性与特殊性，储罐结构冲击失效及其次生爆炸灾害必将带来生命和财产的重大损失。因此，对该类结构提出合理的抗冲击性能评估以及冲击防御设计理论与方法，确保LNG储罐结构在重大灾害中的安全、减少灾后损失，具有重要的研究意义。

目前，针对核电站安全壳、大坝等大体积钢筋混凝土结构及网壳等大跨空间结构的抗冲击性能已经取得相对丰富的研究成果[1-6]，而对大型LNG储罐混凝土外罐抗冲击性能的研究较少。张云峰等[7]运用LS-DYNA软件，模拟质量块撞击储罐的不同位置，分析LNG储罐外罐在冲击荷载作用下的动力性能和储罐的破坏情况。苏娟等[8]借助ANSYS有限元软件，考虑了储罐空罐和满罐两种工况，对冲击荷载作用下LNG混凝土储罐的动态响应进行分析，得到了储罐各控制点的内力时程曲线。崔利富等[9]基于LS-DYNA软件，对160 000 m3的LNG储罐进行冲击模拟，结果表明：战斧巡航导弹冲击LNG储罐影响范围有限，仅产生局部破坏；预应力筋具有一定的阻抗冲击作用的能力。各类规范中，针对LNG储罐结构抗冲击的设计条款极少，仅英国标准BS 7777-1[10]中提到，储罐应具有抵抗飞行物冲击的能力，并给出了推荐的冲击参数：质量50 kg的刚体以45 m/s的速度进行撞击。由此可见，针对LNG储罐抗冲击性能的研究主要集中在冲击后储罐结构的动力响应及破坏特点，而冲击荷载作用下LNG储罐混凝土外罐的失效模式及失效机理研究较少。

本文中，基于全容式160 000 m3的LNG储罐，应用ANSYS/LS-DYNA有限元软件建立LNG储罐混凝土外罐精细化有限元数值模型，通过模拟分析冲击物撞击下LNG储罐穹顶结构的动力响应及其规律，提出混凝土穹顶的失效模式，并根据冲击过程中能量的传递特点揭示其失效机理。最后，研究不同冲击物直径、冲击位置、冲击角度(冲击物速度方向与被冲击面法线的夹角)对混凝土穹顶最大响应及失效模式的影响规律。

1 冲击模拟方法验证

图1 弹丸靶板有限元模型Fig.1 FE model

为验证本文中有限元建模及分析方法和混凝土本构模型的适用性，对文献[11]中弹丸冲击混凝土靶板实验进行数值模拟。弹丸质量588～597 g，弹长150 mm。靶板分素混凝土和钢筋混凝土两种：素混凝土靶板为圆形，直径为1 200 mm，由豆石(粒径小于10 mm)、水泥砂浆浇注；钢筋混凝土靶板的钢筋采用冷拔低碳钢丝，直径4 mm，间距40 mm，抗拉强度平均值为706.2 MPa，弹性模量为205 GPa。实验中测量了弹丸到达靶板时的入射速度以及穿出靶板后的残余速度。运用ANSYS/LS-DYNA有限元软件对弹丸冲击靶板进行数值模拟。混凝土靶板及子弹均采用实体单元Solid 164模拟，钢筋采用杆单元Link 160模拟，钢筋与混凝土之间连接采用约束方程法实现。计算中假定：(1)冲击物是刚性体；(2)冲击作用下只考虑动能和应变能的变化，不计热能的损失；(3)冲击过程中忽略摩擦作用。有限元模型如图1所示。

钢筋材料选用随动塑性强化模型[12]，材料参数分别为[12]：ρ=7 950 kg/m3,E=205 GPa,rP=0.28,Ysig=706.2 MPa,Etan=500 MPa,β=0,SRC=0,SRP=0,εf=0.25。混凝土材料模型初步确定HJC(Johnson-Holmoguist concrete)[12]和CSCM两种形式，本文中通过对比，希望从中选择最佳的本构模型用于LNG储罐有限元冲击数值分析。HJC模型是常用的混凝土模型，虽然能够描述混凝土在大应变、高应变速率和高压下材料的动态响应，但对混凝土材性指标参数要求繁琐；HJC模型参数分别为[12]：ρ=2 500 kg/m3,G=14.86 GPa,A=0.79,B=1.60,C=0.007,Sf,max=7,εf,min=0.01,N=0.61,T=4 MPa,D1=0.04,D2=1.0,K1=85 GPa,K2=-171 GPa,K3=208 GPa。而CSCM模型用来模拟道路两边钢筋混凝土防护结构与车辆碰撞的动态性能[13]，由于所需要输入的参数较少，仅获得混凝土的强度、骨料粒径等参数即可，因此应用相对便利；CSCM模型参数分别为[12]：ρ=2 500 kg/m3,INCRE为0,IRATE为1,ERODE为1.1,RECOV为10,PRED为0.4。

通过对文献[11]中12种工况进行数值模拟，得到贯穿靶板后子弹的残余速度，图2是子弹贯穿后混凝土靶板破坏的实验及模拟结果。当子弹与靶板接触时，击中点附近混凝土单元瞬间失效删除，同时靶板内产生与子弹速度方向相同的球面应力波，当应力波到达靶板背面时形成反射拉伸波，靶板背面混凝土单元产生拉伸破坏，单元被删除。随后子弹继续贯穿靶板，最终混凝土靶板被击穿，击穿孔洞直径大于子弹直径，整个孔洞呈漏斗状。通过比较可得，数值模拟所得到的靶板破坏结果与实验现象基本一致。实验结果与有限元模拟得到的子弹残余速度对比见表1，通过对比两种材料模型的误差，CSCM模型精确度更高，因此我们将采用该模型进行模拟。

图2 靶板破坏现象Fig.2 Impact perforation

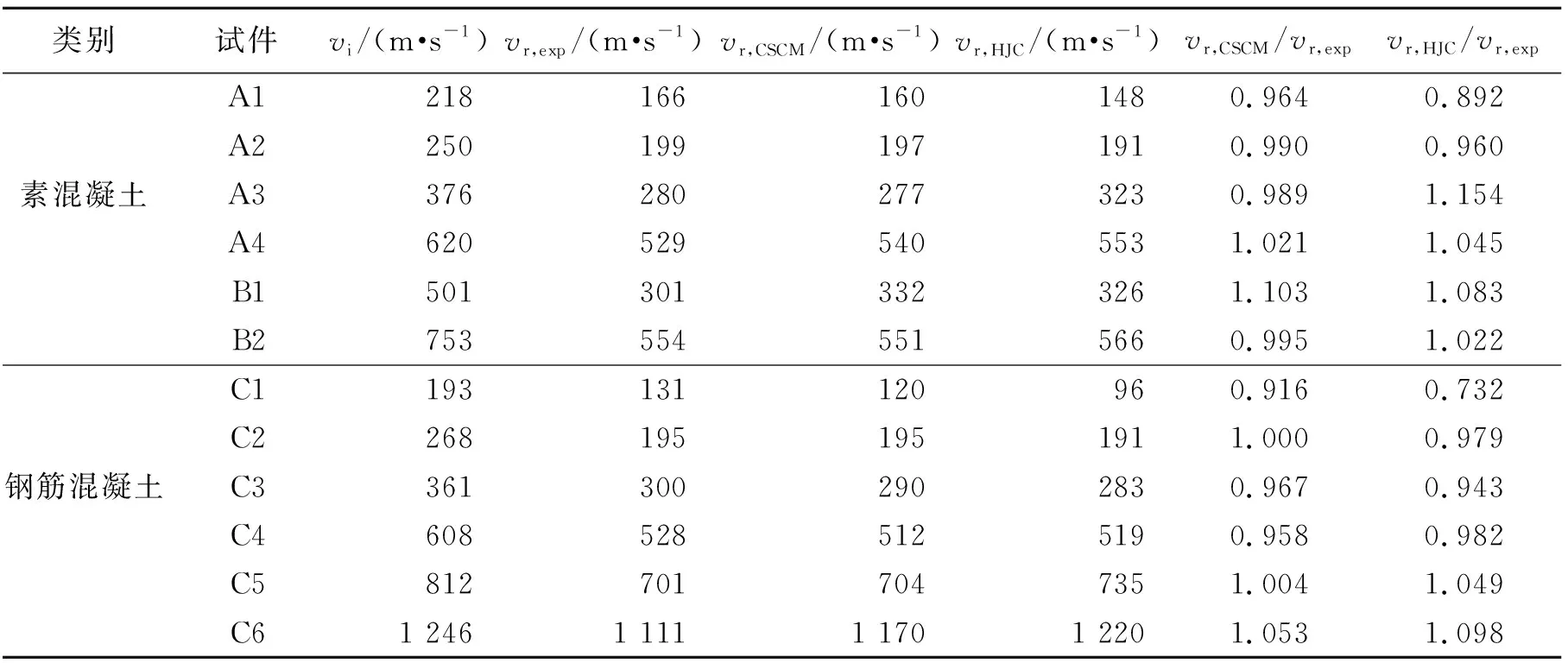
类别试件vi/(m·s-1)vr,exp/(m·s-1)vr,CSCM/(m·s-1)vr,HJC/(m·s-1)vr,CSCM/vr,expvr,HJC/vr,expA12181661601480.9640.892A22501991971910.9900.960素混凝土A33762802773230.9891.154A46205295405531.0211.045B15013013323261.1031.083B27535545515660.9951.022C1193131120960.9160.732C22681951951911.0000.979钢筋混凝土C33613002902830.9670.943C46085285125190.9580.982C58127017047351.0041.049C61 2461 1111 1701 2201.0531.098

2 LNG储罐工程概况及有限元模型

160 000m3大型全容式LNG储罐，由预应力混凝土外罐和9%镍钢内罐两部分组成。外罐由混凝土圆柱壳、球面穹顶、底板和桩基构成，各部分参数如下：混凝土外罐内直径为82 m，高度为38.55 m，壁厚为0.8 m，扶壁柱截面尺寸为4.22 m×1.40 m，环梁截面尺寸为1.05 m×1.56 m，穹顶的曲率半径为82 m，矢高为10.975 m。穹顶中心处混凝土厚度为0.6 m，边缘处厚度为0.8 m。底板的厚度为0.9 m，直径为88 m，采用桩基础。混凝土等级为C50，剖面图如图3所示。

运用ANSYS/LS-DYNA有限元分析软件，建立LNG储罐混凝土外罐的计算模型，混凝土外罐及冲击物均采用Solid 164实体单元。其中冲击物为圆柱体，高度为4 m，直径为1 m，材料模型采用刚性体模型。混凝土采用CSCM模型，通过侵蚀失效准则来模拟混凝土单元的失效，当混凝土的有效塑性应变达到0.1时，单元在后续的有限元计算中即被删除。混凝土与冲击物之间采用面面侵蚀接触(ESTS)，在侵蚀接触下，若模型受冲击部分的单元失效则该单元被删除，但剩余部分的单元仍能继续考虑接触。LNG储罐混凝土外罐有限元模型，如图4所示。为了提高计算效率，节约时间，通过试算，将穹顶动力响应相对较大的区域定义为冲击区，在冲击区域局部进行加密，加密区与非加密区交界处采用点面固连接触，将加密区边界节点约束、限定在非加密区的主面上，从而实现两者的连接。另外，本文中主要针对穹顶大体积混凝土结构抗冲击性能及其破坏机理，因此建模时忽略穹顶内部钢衬板在冲击过程中的有利作用，涉及相关带钢衬板穹顶的LNG储罐的冲击响应分析将是我们的后续研究方向。

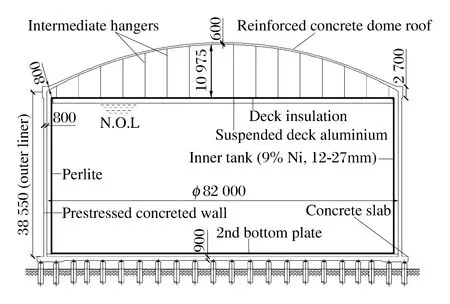
图3 LNG储罐剖面图Fig.3 Profile map of LNG tank

图4 LNG储罐有限元模型Fig.4 FE model of LNG outer tank

3 LNG储罐外罐穹顶结构失效模式

以冲击LNG储罐混凝土外罐穹顶为例，通过改变冲击物的直径(D=1,4 m)、冲击角度(0°、45°)、冲击位置见图5中A、B两点，A、B水平距离为20.5 m，进行大规模参数分析，得到穹顶结构在冲击荷载作用下的失效模式。

图5 冲击位置示意图Fig.5 Locations A and B at dome

储罐与冲击物的有限元模型如上所述，保持冲击物形状不变，改变冲击物的质量和初始冲击速度对储罐穹顶进行冲击。通过试算，选取最小的冲击荷载和冲击速度为250 kg和10 m/s，当冲击荷载继续减小时储罐结构产生的动力响应不再明显，没有研究价值。最大的冲击荷载和冲击速度取为10 t和200 m/s，在此基础上，即使继续增大冲击质量或速度，储罐结构的失效模式也不会改变。冲击物质量分别取为0.25、0.5、1、5、10 t，冲击速度分别取为10、20、30、40、50、60、70、80、90、100、150、200 m/s。

通过对上述240种工况进行模拟分析，得到冲击荷载作用下LNG储罐混凝土外罐穹顶结构的失效模式主要有3种，分别为局部凹陷、混凝土剥落、击穿破坏。

当冲击物初始能量较小时，穹顶在冲击位置处产生凹陷和裂纹，与冲击物直接接触区域的单元进入塑性，但并未有单元失效破坏，储罐仍处于安全状态，将这种失效模式称为局部凹陷。

在穹顶发生局部凹陷的失效模式之后，继续增加冲击物的初始能量，在更大的冲击能量作用下，穹顶内侧混凝土先出现剥落现象，未剥落的混凝土伴随有一定程度的凹陷，但穹顶并未被穿透，对LNG内部钢罐仍具有一定的保护作用，将这种失效模式称为混凝土剥落。

当初始冲击能量继续增大，继混凝土发生剥落破坏之后，穹顶中心混凝土被击穿，与冲击物直接接触的单元全部失效破坏，混凝土外罐发生损坏，不再对内罐起到保护作用，将这种失效模式称为混凝土击穿破坏。

根据各工况穹顶的破坏情况绘制出3种失效模式的分布，如图6所示。

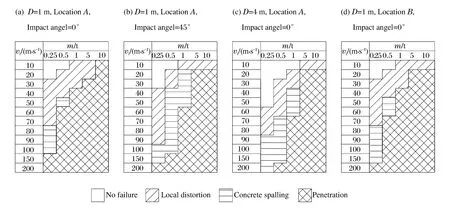
图6 失效模式分布图Fig.6 Distribution of failure modes

4 LNG储罐外罐穹顶结构失效规律

4.1 冲击角度对失效模式的影响

在冲击过程中，冲击物的冲击方向是不确定的，因此需要考虑冲击角度对储罐穹顶结构的影响。为研究冲击角度对LNG储罐失效模式的影响规律，选择0°、45°两种角度对LNG储罐穹顶中心位置进行冲击模拟。

通过分析失效模式分布(见图6(a)～(b))可知，冲击角度对失效模式的影响不可忽略。冲击物以45°冲击时击穿破坏所占的面积小于0°冲击时所占面积，并且达到每一种失效模式所需初始能量均上升，这表明当冲击角度较大时，在初始冲击能量相同的情况下，LNG储罐结构破坏程度更轻。这也同样说明，冲击角度较大时需要更多的能量才能使储罐产生严重的破坏，因此最不利冲击角度为0°。

以0°、45°两种冲击角度下的两个典型算例(m=1.0 t，v=50 m/s)分析冲击角度对破坏模式的影响规律，并从冲击荷载、冲击物速度、储罐应变能3个角度揭示其原因。

(1)图7为两种工况下冲击力曲线。当冲击角度为45°时，冲击物与穹顶有2次撞击过程，当冲击物顶部与穹顶接触碰撞之后，冲击力在冲击瞬间达到峰值12.8 MN，持续 7ms后下降为零。冲击物与穹顶碰撞后速度方向发生改变，绕长度方向发生旋转，冲击物尾部与穹顶再次发生碰撞，冲击力第2次达到峰值27.8 MN，持续4 ms后下降为零。当冲击角度为0°时，冲击力在冲击瞬间达到峰值22.8 MN后不断衰减，0.06 s后整个冲击过程结束。2次碰撞的冲击力峰值虽然相近，但由于45°冲击时冲击力持续时间过短，穹顶结构变形并不完全，因此仅发生混凝土剥落，并未发生穿透现象。

(2)图8为两种工况下冲击物的速度曲线。当冲击物以45°冲击穹顶时，在第1次碰撞后冲击物速度由50 m/s下降为34.8 m/s，当冲击物尾部2次撞击后速度短暂下降为31.5 m/s，后逐渐恢复为34.8 m/s后保持稳定。而0°撞击时，速度瞬间下降为1.56 m/s，可见45°冲击后冲击物仍剩余大量动能，能量并未完全传递给穹顶，转化为穹顶的应变能。而当冲击物以0°冲击穹顶时，冲击物将绝大部分动能传递给穹顶，穹顶吸收和转化的能量远大于45°的，因此冲击角度为0°时穹顶破坏更严重，混凝土被击穿。

图7 冲击力Fig.7 Impact force

图8 冲击物速度Fig.8 Velocity of impactor

(3)从能量的角度也可以解释发生两种不同失效模式的原因。图9(a)为45°冲击时穹顶应变能曲线，穹顶应变能有2次跃升，分别对应冲击物首尾2次撞击穹顶。第1次撞击后穹顶破坏较小，应变能损失较少，仅为40.4 kJ，而第2次碰撞损失能量为150 kJ，由此可见第2次碰撞后穹顶结构损坏更严重。冲击角度为0°的工况下穹顶应变能曲线如图9(b)所示，在冲击瞬间穹顶应变能迅速增加，达到峰值552 kJ，之后随着穹顶混凝土破坏程度加深，失效的混凝土单元带走大部分能量，最终穹顶应变能保持在较低水平。

图9 穹顶应变能Fig.9 Internal energy of dome

通过以上研究分析可以得到，当冲击物以不同冲击角度冲击LNG储罐穹顶时，储罐的失效模式随冲击角度的改变而变化明显，冲击角度为0°时储罐结构失效模式最为严重。其原因主要是，由于冲击角度减小时冲击物撞击穹顶后反弹程度降低，这就使得冲击物自身动能下降更多，从而对储罐穹顶做功更多，因此穹顶的破坏就更加严重。但是当冲击角度增大时，冲击物撞击穹顶后冲击速度方向发生改变，可能会对穹顶发生2次碰撞，这也会对穹顶造成一定程度的损伤，这部分的损伤也较大，不可忽略。

4.2 冲击物尺寸对失效模式的影响

为研究冲击物尺寸对LNG储罐失效模式的影响，采用直径为1、4 m，高度均为4 m的两种圆柱体冲击物竖直向下冲击穹顶中心。通过分析失效模式分布(见图6(a)、(c))可得，当冲击物直径增大时，未破坏和局部凹陷这两种破坏程度轻微的失效模式所占据的面积扩大，而击穿破坏的范围缩小很多，取而代之的是混凝土剥落的失效模式。总体来说，当初始冲击能量相同时，随着冲击物直径的增大，储罐的破坏程度降低。但是增大冲击物直径时，冲击区范围增大，穹顶结构的动力响应有一定程度的增加。

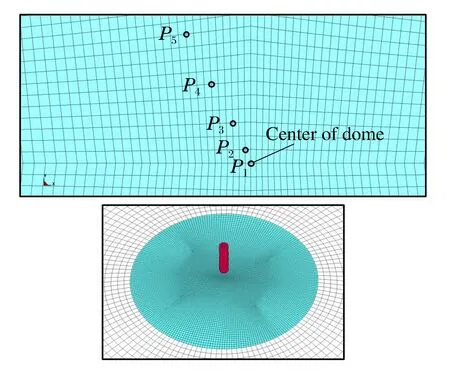
图10 节点位置示意图Fig.10 Designation of points

以直径为1、4 m两种冲击物的两个典型算例(m=1.0 t，v=50 m/s)分析冲击物直径对破坏模式的影响规律，图10为节点位置示意图。

图11为两种工况的位移曲线，由图可见，两组曲线差异较大。当D=1 m时，在发生碰撞后点1位移在短时间内达到峰值0.12 m后单元失效，位移时程曲线中断。由于失效单元带走了大部分能量，并且碰撞持续时间太短，单元删除前能量传递尚未完成，因此除点1外其余各点最终位移均较小。当D=4 m时，点1位移峰值为0.077 m，达到峰值后混凝土一部分变形发生恢复，最终位移稳定在0.058 m，点2最终位移稳定在0.03 m，其余3点最终位移稳定在0.01 m。由此可见，在冲击物的质量和初始速度相同的情况下，当冲击物直径较大时，穹顶破坏程度减轻，但受冲击影响的范围增大。

穹顶应变能变化曲线可以更直观地反映，整个冲击过程穹顶的变形发展与单元的失效过程。当D=1 m时，穹顶应变能曲线如图12(a)所示，冲击开始时总应变能曲线与未破坏单元应变能曲线保持重合，达到峰值552 kJ后两条曲线逐渐分离，失效破坏的混凝土单元带走能量628 kJ，剩余单元应变能急剧下降至64.7 kJ。当D=4 m时，穹顶应变能曲线如图12(b)所示，在冲击瞬间穹顶应变能迅速增加，达到峰值后随着混凝土发生回弹及部分混凝土失效，应变能有略微下降，最终应变能保持在521 kJ，穹顶内侧破坏的混凝土单元带走能量182 kJ。通过比较两种工况下应变能曲线，可以很明显看出，冲击结束后D=1 m工况穹顶残余变形较小，破坏的混凝土单元更多，穹顶破坏更严重。

图11 节点位移Fig.11 Displacement of point

图12 穹顶应变能Fig.12 Internal energy of dome

由此可得，在冲击物的质量和初始速度相同的情况下，减小冲击物的直径会使得储罐的动力响应更大。但是一旦储罐发生破坏，由于与储罐直接接触的面积增大，冲击物传递到储罐结构的能量更多，大直径的冲击物反而会对储罐造成更严重的破坏。

4.3 冲击位置对失效模式的影响

除冲击物直径、冲击角度，由于穹顶混凝土厚度不均，因此冲击位置对失效模式的影响同样值得关注。为研究冲击位置对LNG储罐失效模式的影响，选择穹顶上A、B两处进行冲击，冲击角度均为0°。A、B两点位置如图5所示。通过分析失效模式分布(见图6(a)、(d))可得，两种工况下失效模式的分布较为相似，结构无破坏和局部凹陷两种轻微失效模式的分布范围相同，当冲击物冲击B点时，击穿破坏所占据的面积略有减小。这说明，改变冲击物冲击穹顶的位置对穹顶破坏模式的影响较小，但是由于穹顶混凝土厚度不均，中央位置处混凝土厚度最小，因此冲击此处时破坏程度略有加重，发生击穿破坏的可能性更大，由此可知穹顶中央位置为冲击的最不利位置。

以两个不同冲击位置的典型算例(m=1.0 t，v=50 m/s)来分析冲击位置对破坏模式的影响规律。

从能量角度对比分析两种工况下穹顶的动力响应。当冲击穹顶中心时，穹顶应变能如图13(a)所示，未破坏单元应变能峰值为552 kJ，后下降至64.7 kJ保持稳定，破坏失效单元损失能量为628 kJ，整个过程中冲击物传递给穹顶的总应变能为692 kJ。当冲击B点时，穹顶应变能曲线如图13(b)所示，两组曲线变化趋势近乎相同，仅在数值大小上略有差异。通过对两种工况下应变能大小的比较可以看出，冲击A点时冲击物传递到穹顶的应变能相对比冲击B点较小，破坏损失的能量也较少。其原因主要是，由于穹顶的混凝土厚度不均，穹顶中心处混凝土厚度最小为0.6 m，而穹顶边缘处混凝土厚度达到0.8 m，因此冲击穹顶不同位置时虽然穹顶的失效模式相同，但是冲击过程中穹顶所吸收的能量大小及动力响应存在一定差异。

图13 穹顶应变能Fig.13 Internal energy of dome

通过对两种工况的分析可得，当冲击物沿穹顶法线的方向冲击时，冲击位置对穹顶失效模式的影响不大，冲击作用下穹顶的动力响应略有不同，但各个响应的变化趋势以及最终状态差别较小，可以忽略。

5 冲击失效机理

从能量的角度来研究一下储罐的失效机理。以能量为研究对象，产生3种不同失效模式的原因主要是：由于冲击物的初始能量不同，初始能量较小时，储罐结构在冲击物作用下产生局部凹陷，随着冲击能量的增加，逐渐出现混凝土剥落及冲切破坏的失效模式。从能量的角度出发，整个冲击过程总共可分为3个阶段：冲量施加，能量传递，能量转换与消耗。这3个过程并没有严格的界限区分，冲量施加的过程中能量传递也同时在进行，能量传递过程也伴随着转化和消耗，但是其中一个过程起主导作用。以下将通过具体的情况来说明各种失效模式的失效机理。

5.1 局部凹陷失效机理

以局部凹陷(m=1.0 t，v=25 m/s)为例，具体分析局部凹陷的失效机理。将冲击力达到峰值定义为关键时刻t1、冲击物与储罐分离定义为关键时刻t2。由图14可见，冲击力曲线被上述两个关键时刻划分为3部分，分别对应3个阶段。整个冲击过程中LNG储罐混凝土外罐各部分应变能随时间变化曲线，如图15所示。

图14 局部凹陷全过程划分示意图Fig.14 Partition of failure process for local distortion

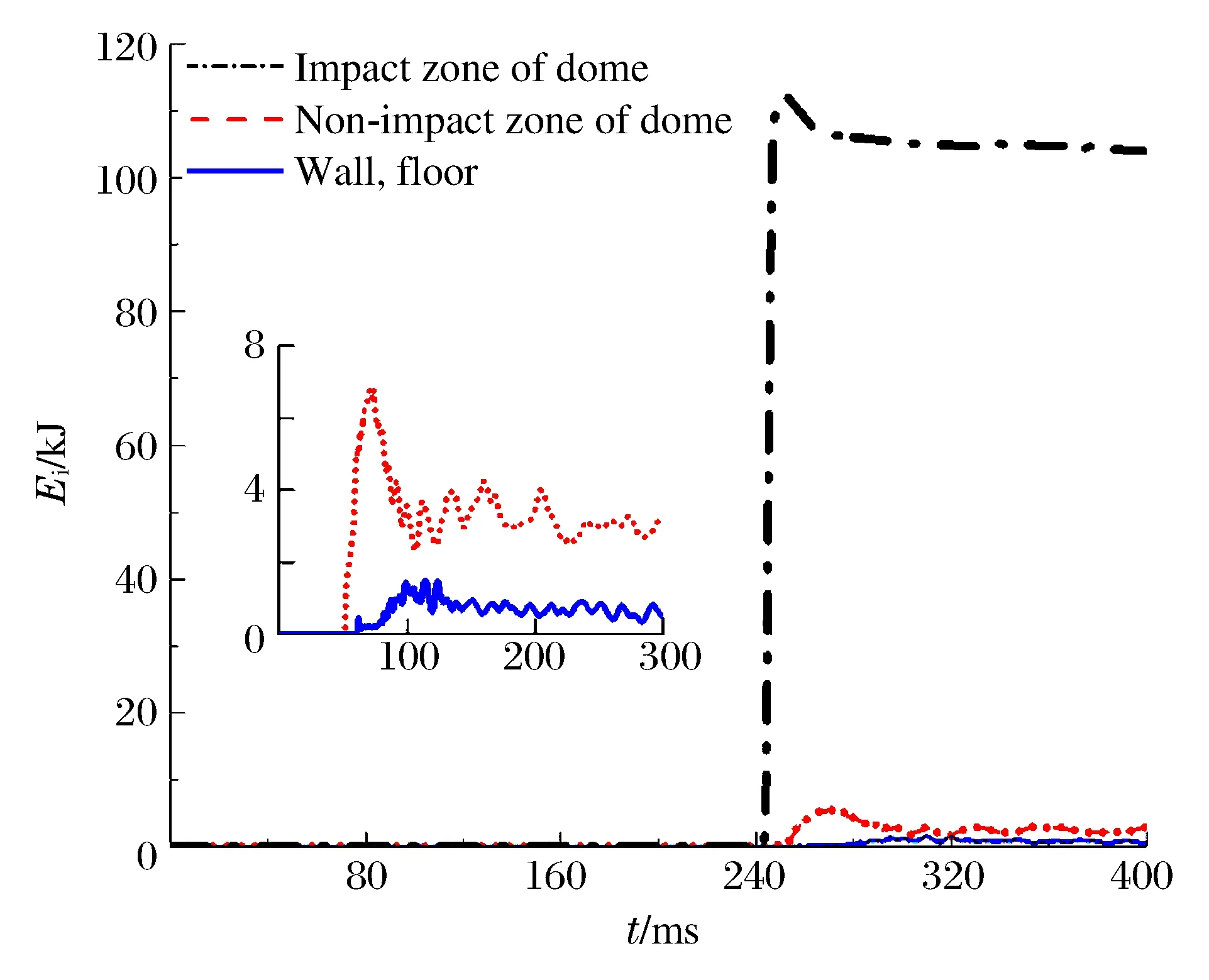
图15 穹顶应变能Fig.15 Internal energy of dome

冲量施加阶段指的是冲击物与穹顶接触碰撞的阶段，在此阶段中，冲击物将自身动能施加给穹顶，穹顶与冲击物直接接触的区域获得了较大的能量，产生了局部凹陷，由于冲击持续时间极短，非冲击区的动力响应并不明显。能量的传递阶段指的是冲击区将得到的能量向非冲击区域传递的阶段，在这个过程中，冲击物与储罐穹顶不再接触，应力呈环状由穹顶中心向外传播，非冲击区得到能量后动力响应增大，但是由于冲击物初始能量较小，能量传递的范围也较小，非冲击区产生的变形有限。

能量的转换与消耗阶段指的是冲击物与穹顶分离后的阶段，在此阶段中，由于反弹作用冲击物逐渐飞离穹顶，穹顶冲击区域节点的速度减小至零后反向增加，节点位移略有减小，穹顶恢复一部分变形。随着时间发展，冲击区混凝土单元的振动逐渐停止，穹顶结构的动能完全消失，应变能稳定不变，整个冲击过程结束。

5.2 混凝土剥落与击穿破坏失效机理

图16～17为混凝土剥落(m=0.25 t，v=100 m/s)、击穿破坏(m=1.0 t，v=100 m/s)两种失效模式典型算例所对应的冲击全过程划分示意图及穹顶应变能变化曲线。通过两组曲线可以看出，尽管两种失效模式下结构破坏过程不同，但两者能量曲线的变化趋势相近，因此将两种失效模式作对照共同分析其失效机理。

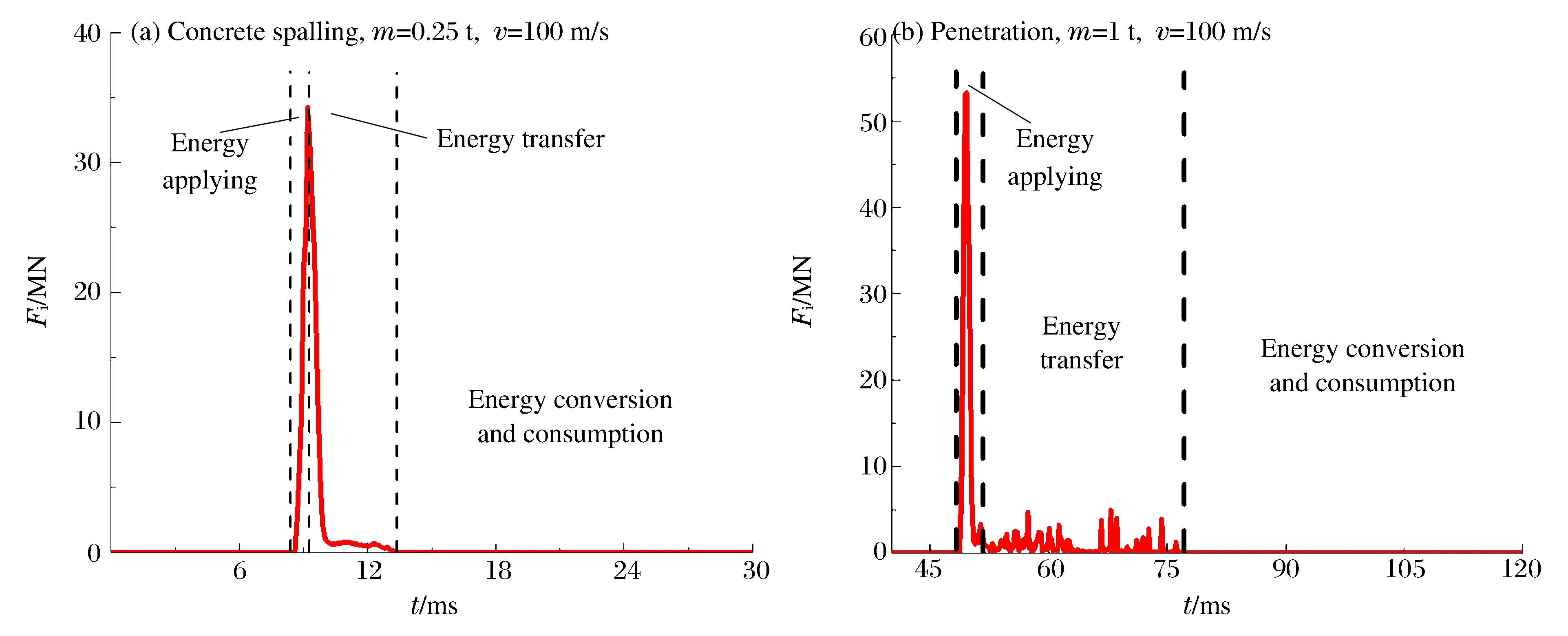
图16 冲击全过程划分示意图Fig.16 Partitions of failure process for impact

图17 穹顶应变能Fig.17 Internal energy of dome

通过两组曲线可以看出，冲击力在撞击瞬间达到峰值后迅速下降，从冲击物与穹顶接触开始到冲击力急剧下降结束，整个过程为冲量施加阶段。在此阶段中，冲击物将能量传递到穹顶，穹顶吸收足够的能量后混凝土发生破坏，被冲击物击穿。由于混凝土破坏后带走了大部分能量，导致穹顶剩余部分动力响应相对较小。当出现混凝土剥落的失效模式时，穹顶内侧混凝土先破坏，其原因是：冲击物与穹顶接触后，应力波从撞击位置处向穹顶内侧传播，当应力波传播至穹顶内侧表面时形成反射拉伸波，由于采用了侵蚀失效准则中主应变失效方式来模拟混凝土单元的失效，当混凝土单元的主应变达到所设置的阀值(0.1)时，此单元即判定为失效并被删除，因此穹顶冲击区内侧混凝土因发生拉伸而首先破坏。与混凝土剥落模式中由于应力波传播而导致穹顶内部混凝土先破坏的情况不同，当发生击穿失效模式时，与冲击物直接接触部位的混凝土在撞击瞬间即发生冲切破坏，冲击物击穿穹顶进入储罐内部。

从冲击力在低水平范围内波动到混凝土单元失效剥落完成，为能量的传递阶段。在与穹顶持续接触的过程中，冲击物将剩余能量继续传递给穹顶，穹顶将获得的能量呈环形向外传递扩散，冲击区与非冲击区的应力与变形水平均上升。当冲击物击穿混凝土完全进入穹顶内部后，冲击力彻底下降为零，混凝土单元失效删除结束，穹顶剩余部分的能量不再减少。洞口附近混凝土由于惯性继续振动，动能与应变能相互转化，最终穹顶应变能曲线保持稳定，结构达到平衡状态。