内爆压缩多层密绕螺线管的数值模拟*
2018-09-27张春波宋振飞谷卓伟赵士操
张春波,宋振飞,谷卓伟,卢 纪,赵士操
(1.中国工程物理研究院流体物理研究所,四川 绵阳 621999; 2.中国工程物理研究院计算机应用研究所,四川 绵阳 621999)
20世纪50~60年代,MC-1型柱面内爆磁通量压缩发生器(explosive magnetic flux compression generator)技术原理由苏联萨哈洛夫院士首先提出[1]。它利用炸药柱面内爆驱动金属套筒压缩其内部预先引入的磁通量,将炸药化学能转化为电磁能,使磁通量在轴线附近小体积内聚积从而实现超强磁场。然而,在实验过程中,由于金属套筒在内爆压缩过程中容易发生结构失稳,实际中难以获得稳定的超高磁场[2]。20世纪80~90年代,苏联实验物理研究院Pavlovskii院士的团队提出了多级MC-1技术[3]。其实验原理如图1所示,电容器组放电使得线圈在套筒内产生一个初始磁通量,炸药内爆压缩初级套筒,当初级套筒失稳后,次级套筒继续压缩磁通量,最终在套筒轴心区域实现很高的磁通量密度。由于采用多级套筒结构,套筒承受的压力和磁场梯度降低,前一级套筒在失稳前将被后一级套筒所取代,从而保证磁通量最终被有效汇聚。Pavlovskii[4]利用这个技术实现了2 000 T以上的超高磁场。在多级MC-1技术中初级套筒是采用一种特殊的多层密绕螺线管结构[4],如图2所示。

图1 多级MC-1装置实验原理图Fig.1 Schematic of cascades MC-1 experiment in exploded magnetic field
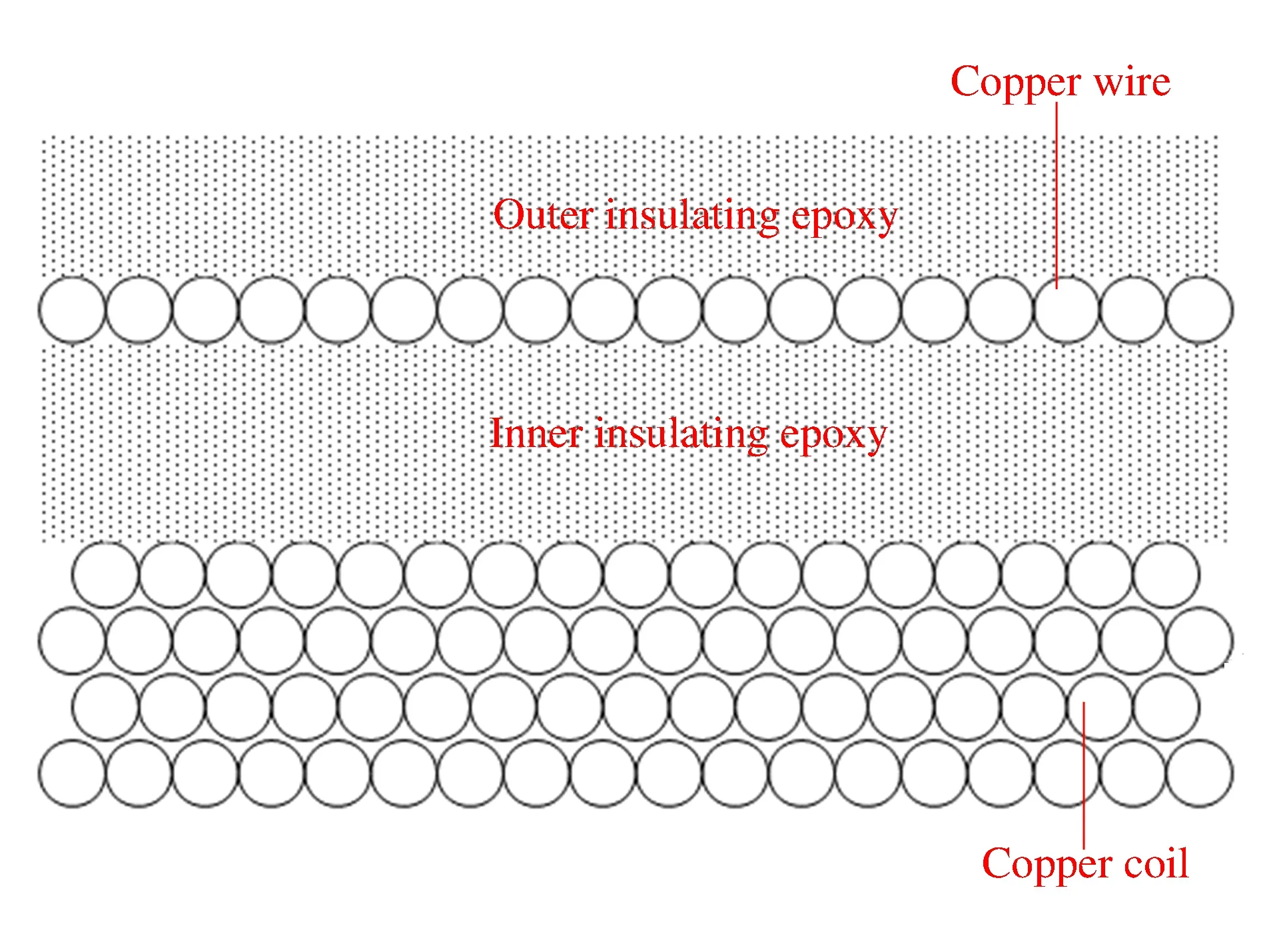
图2 多层密绕螺线管壁截面结构示意图Fig.2 Fragmental picture of coil cross-section
开展内爆压缩多层密绕螺线管结构的数值模拟研究,对于深入研究多级MC-1技术具有重要意义,目前在这个方面研究相对较少。Hayhurst等[5]建立了陶瓷纤维、Kevlar纤维布在超高速撞击条件下的材料模型,并通过实验和数值模拟(SPH方法)对材料模型及其参数进行了比较。赵士操等[6]应用SPH方法,对纤维增强复合材料的纤维结构和基体建立计算模型,研究不同纤维编织方法的复合材料压缩性能,以及复合材料在冲击载荷下的破坏过程。龚芸芸等[7]利用气炮发射平面飞片冲击压缩铜丝阵结构,并用SPH方法建立丝阵结构动力学计算模型,计算的界面速度峰值与实验测试数据吻合。
本文中,针对多层密绕螺线管的结构特点,采用AUTODYN软件二次开发程序建立数值计算模型,计算内爆压缩过程中多层密绕螺线管的动态力学响应,并分析螺线管螺旋角度与铜线直径对结构界面不稳定扰动发展的影响,以期为后续开展密绕螺线管结构设计提供参考。
1 数值建模
多层密绕螺线管属于非均匀、非密实三维螺旋结构,若采用有限元法建立模型,将难以高效处理计算网格的急剧变形以及铜线单元之间的非线性接触问题。光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)方法[8]可以将整个流场的物质离散为一系列具有质量和速度的粒子,采用核函数计算,求解流场中不同位置不同时刻的各动力学量。本文中采用无网格SPH方法建立数值模型,可有效避免大变形时网格畸变和单元非线性接触等问题。
1.1 几何模型
选取与实验[4]一致的螺线管结构参数,螺线管结构如图2所示。内、外径分别为92和102 mm,平均初始密度为6.2 g/cm3,总厚度为5 mm(其中铜线层厚2.0 mm,中间环氧层厚1.5 mm,铜线折返层厚0.5 mm,外环氧层厚1.0 mm)。根据螺线几何参数方程,采用Matlab软件生成三维螺线粒子空间坐标和方向,如图3(a)所示。应用Autodyn二次开发接口EXEDIT子程序将SPH粒子沿储存的螺线坐标一一放置,完成内层螺线圈建模;在已建立的螺线圈外层充填SPH粒子建立铜线层和绝缘层,建立的完整螺线管结构如图3(b)所示,其中铜线粒子尺寸为0.4 mm,环氧粒子尺寸为0.5 mm。

图3 三维螺线管套筒结构的模拟Fig.3 Simulation structure of 3D solenoid liner
1.2 周期镜像边界
若建立全尺寸SPH螺线管模型,计算粒子数将达600万以上。考虑到多层密绕螺线管结构沿轴向的周期性,仅选取中间一段螺线管结构进行计算,将SPH粒子计算规模减少到279万。对选取的螺线管结构,在轴向两端若采用固定约束或自由边界条件,将引入边界处应力波的反射,因此需要采用周期镜像边界来进行相关计算。由于AUTODYN[9]不具备对模型施加周期边界条件,对于非密实复合材料,本文中通过设置镜像区实现周期加载条件。如图4所示,将边界A区域镜像到B区域的上端形成镜像区A′,将边界B区域镜像到A区域的下端形成镜像区B′,而模型中心C区域保持不变。通过镜像区循环赋值,消除应力波在模型边界处的反射。

图4 周期边界镜像示意图Fig.4 Schematic drawing of mirroring periodic boundary
2 结果与分析
2.1 螺线管爆轰压缩过程
在爆轰加载方面,如果炸药采用欧拉算法,则与SPH算法难以高效耦合,因此采用二维轴对称模型获得爆轰加载边界。计算模型如图5(a)所示。模型中,铜材料采用冲击物态方程[10]及Johnson-Cook材料本构模型[11],材料屈服强度设为1.2 GPa;高能炸药高55 mm、厚65 mm,材料选取PBX-9404-3,采用JWL状态方程[10],二维爆轰加载计算结果如图5(b)所示。

图5 二维螺线管的模型和计算结果Fig.5 Numerical simulation of 2D solenoid

图6 爆轰压缩密绕螺线管的数值模拟Fig.6 Numerical simulation of 3D solenoid under implosive compression
将图5(b)结果作为三维计算中加载边值条件,获得多层密绕螺线管内爆压缩过程的数值模拟结果,如图6所示。从图可看出,在内爆压缩前中期,螺线管结构内表面相对光滑;当螺线管平均半径压缩至1.58 cm时,结构内表面已出现显著的不稳定扰动;在螺线管平均半径压缩至1.0 cm时,结构内表面失去稳定性最终形成花瓣状变形。采用粒子径向位移的标准方差σ(r),反映内爆压缩过程中内表面的不稳定扰动增长:
(1)


图7 内爆压缩实验中多层密绕螺线管在不同时刻的闪光X射线照片Fig.7 X-ray photographs of a single-cascade cross-section at different moments of its operation
2.2 螺旋角度和铜线直径对结构动力学响应的影响
多层密绕螺线管是非密实、非均匀结构,在制备过程中螺旋角度和铜线直径等结构参数将是影响其压缩性能的关键因素。为此,从工程应用角度初步分析螺旋角度和铜线直径对结构不稳定扰动的影响。
(1)螺旋角度对结构界面不稳定性的影响
建立螺旋角度分别为0°、12°和24°的3个螺线管模型,其他参数保持一致。3种计算模型的螺线管初始密度分别为6.21、6.18和6.17 g/cm3,施加相同的速度边界条件,图8给出了内爆压缩后期螺线管结构不稳定性的发展。当螺线结构退化为二维线圈结构,即螺旋角度为0°,结构压缩后期内表面的扰动严重,线圈在环向压力作用下产生十几个屈曲条纹;当螺旋角度升高为12°和24°时,结构内表面不稳定性得到改善。图9给出了不同螺旋角度时结构内表面粒子径向位移的标准方差随时间的增长关系。从图可知,对于不同螺旋角度的螺线管结构,内表面粒子扰动增长趋势一致,但扰动幅值存在显著差异。在内爆压缩初期7.01 μs时,螺线管结构内表面在冲击波作用下出现扰动增长,在7.83 μs时,随着螺线管压实过程趋于稳定,后继惯性压缩过程界面扰动迅速增长。
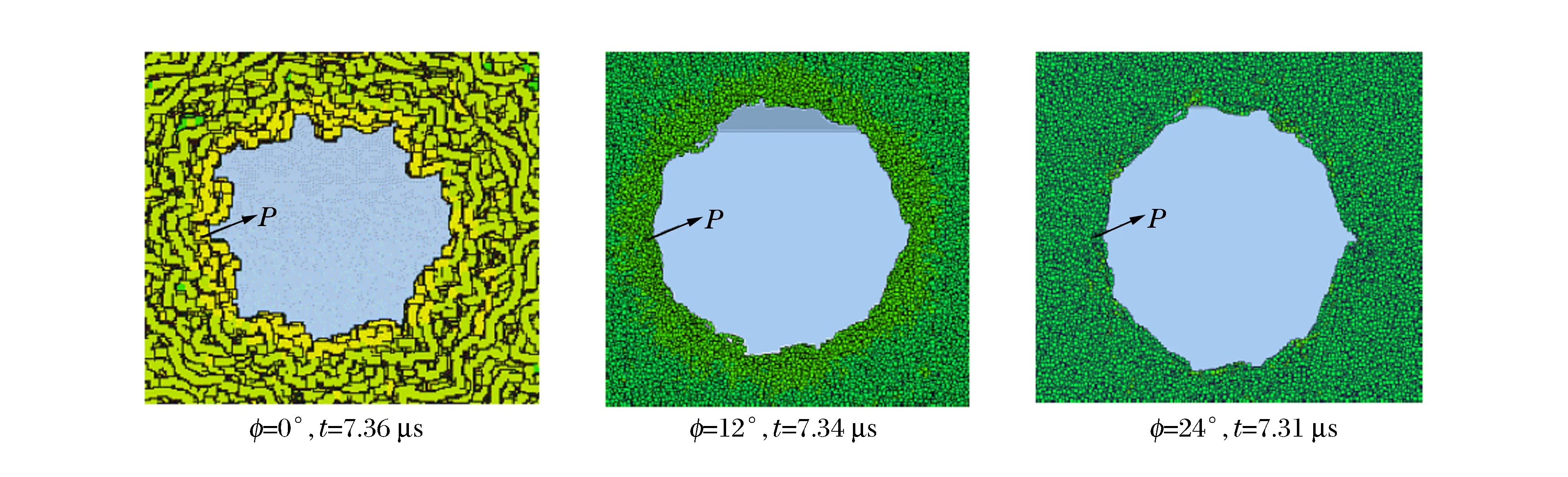
图8 不同螺线角度模型内界面不稳定扰动的数值模拟Fig.8 Numerical simulation of different spiral angle structure under implosive compression

图9 观测点粒子径向位移的方差Fig.9 Observation of particle radial displacement variance changes
具备不同螺旋角度的多层密绕螺线管界面扰动发展过程,如图10所示。螺线管在内爆压缩过程中经历冲击压缩、冲击卸载以及惯性压缩3个阶段。以无螺旋角结构为例,数值计算结果表明:在冲击压缩阶段7.1 μs时,螺线管平均密度由初始时刻的6.21 g/cm3增大至8.39 g/cm3,接近密实铜材料的密度,此时结构P点处压力高达29.3 GPa;在冲击卸载阶段7.6 μs时,螺线圈平均密度下降至7.67 g/cm3,P点处压力下降为1.16 GPa;在7.6 μs之后,螺线管结构发生惯性压缩塑性变形,结构密度持续增加,并且伴随着结构内压力的增长。对于无螺旋角结构,如图10(a)所示,螺线扰动变形主要发生在二维线圈环内,由内往外发展,在螺线管压缩前期8.65 μs时计算出结构P点处的压力为2.49 GPa,而在压缩后期13.36 μs时,结构P点的压力已增大为10.5 GPa。在不考虑强度失效情况下,环内低模数的扰动对应较高结构压力。对于螺旋角度12°与24°结构,如图10(b)与10(c)所示,在压缩初期螺线亦发生三维方向的扰动增长,在压缩的初期8.65 μs时,计算得到结构P点处的压力为2.1 GPa与1.51 GPa,而在压缩后期13.36 μs时,结构P点处的压力增加至3.93 GPa与3.75 GPa。螺线发生高模数不稳定性增长,对应较低的结构压力,此时螺线结构内界面的不稳定幅值相应较低。
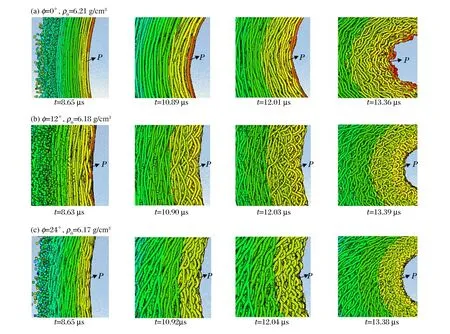
图10 不同螺旋角度下结构扰动的形成过程Fig.10 Formation processes of structure disturbance with different spiral angles
(2)铜线直径对结构界面不稳定性的影响
铜线直径分别为0.25和0.4 mm,初始密度分别为6.17和6.19 g/cm3,结构材料强度、螺旋角度及几何尺寸保持一致,模型施加相同的速度边界条件。如图11所示,螺线管结构内表面粒子径向位移的标准方差计算数据表明:铜线直径为0.25 mm时,在冲击压缩初期7.4 μs至8.5 μs,结构界面不稳定扰动增长较快;铜线直径为0.4 mm时,在冲击压缩初期由于结构需要压实过程,内界面粒子扰动增长慢,在压缩中期8.6 μs至9.5 μs,内界面粒子却呈现出扰动迅速增长,并且在9.4 μs时界面扰动幅度超过铜线直径0.25 mm的。螺线管压缩后期界面失稳发展如图12所示,当铜线直径由0.25 mm增大至0.4 mm,在惯性压缩阶段,结构密度迅速增加,螺线发生低模数的屈曲失稳,对应压缩后期较高的结构压力以及较高的内界面扰动幅值。

图11 观测点粒子径向位移的方差Fig.11 Observation of particle radial displacement variance changes

图12 螺线管结构内界面不稳定性发展的数值模拟Fig.12 Numerical simulation of structure displacement under implosive compression
3 结 论
建立了非均匀三维多层密绕螺线管结构计算模型,利用SPH方法开展了内爆压缩密绕螺线管的流体动力学过程数值模拟。计算结果显示多层密绕螺线管在内爆压缩中后期出现内界面花瓣式不稳定扰动发展,与实验结果[4]基本符合,证明了数值模拟的合理性。数值模拟结果显示:螺线管结构参数包括螺旋角度与铜线直径等,对多层密绕螺线管内爆动力学响应将产生显著的影响,螺旋结构具有一定程度抑制扰动增长的作用;而螺线直径的增大,将加重螺线管结构内界面的不稳定扰动。
通过数值模拟计算得到冲击压缩过程中影响多层密绕螺线管结构稳定性的一些关键因素,为今后多层密绕螺线管的优化设计提供一些重要参考。但由于数值模拟中未采用材料失效模型,导致计算扰动幅值低于实验值,在今后工作中需引入合理的复合结构材料冲击动力学失效破坏判据。
感谢袁红副研究员、周中玉助理研究员等的大力协助。
