结合SCAN方法与离散小波变换的无损彩色图像加密算法

文小爽 张芳君

(河南大学计算机与信息工程学院 河南 开封 475004)

0 引 言

随着互联网技术的飞速发展和日渐成熟，网络在线通信变的越来越受欢迎，同时也带了一系列问题，如个人信息被非法利用，对个人、社会、国家等造成了一系列困扰和不可弥补的影响。由此产生的安全问题也得到更多的关注。因此怎么去安全地保护信息数据和数字产品拥有者的权益，成为了一个异常棘手的问题。

伴随着数字化时代的到来，现如今许多信息内容都以数字化的形式被存储和传输，数字化信息包括文本、图像、音频、视频等多种类型。其中，数字图像因其敏感性、形象直观、易辨性、信息量大等特点，成为网络传输的重要载体之一。因此，对其安全性进行必要的保护成为现今人们关注的重点，国内外研究学者正在提出一系列的加密算法来隐藏图像携带的重要数据信息。混沌由于其初值敏感性和非周期性使其符合研究学者对图像加密的要求。中国“十二五”、“十三五”国家密码发展基金均将混沌密码作为新型密码理论列入其中。美国国家科学基金会和军方研究部门近年来也加大了对混沌密码系统研制的经费投入，欧洲各国政府及科技界也对混沌密码研究投入了大量经费。这些充分显示世界各国政府和国际科技界对混沌密码研究的高度重视。

为了使上述问题得到良好的解决，研究者提出了众多加密方案。由于数字图像本身的独有特点，使得以往的方案如DES、AES、RSA已经达不到密码学的要求。鉴于混沌理论自身包含系统参数和初值极端敏锐性、伪随机性等优良特质，使其达到了数字图像加密得要求，并受到众多专家的关注。在过去几十年中，关于混沌系统的加密算法被大量的探究[1-5]。混沌一般用于产生密钥流，作为图像加密时的密钥。可以将混沌系统大致分为两种类：(1) 一维混沌系统[2-4]，如一维Logistic混沌系统、Sine混沌系统等；(2) 多维混沌系统[4-7]，像Lorenz和Rossler混沌系统，然而高维混沌系统结构复杂、参数多，使得计算难度增加。通过比较这两类系统，不难发现，一维混沌系统较容易实现，得到大范围地应用。然而，在最近几年，国内外学者提出了一系列新的混沌系统，这些新的混沌系统是根据已有的简单混沌系统结合而成，已经被证明其混沌分布范围更广泛，混沌特性更明显。

图像加密大致分为两种：空域加密与频域加密。空域加密即空间域加密，主要是改变图像的位置和像素值，前者称为置乱，后者称为扩散。置乱顾名思义就是扰乱图像矩阵内像素的位置坐标，打破矩阵元素之间的相关性。混淆就是通过混沌系统生成的混沌序列对像素值加以改变，使图像不再具有明文的特征，隐藏重要的明文信息。在分析现如今众多图像加密算法后，不难发现，这两者加密方法都有所涉及[8-12]。为了打破图像像素之间的关联，加密算法通常在空域上直接对像素值进行操作，但据此产生的加密图像不可压缩，同时对误差极为敏感。基于此，国内外学者正在将研究方向转移到频域。频域加密的主要思想是，通过利用离散余弦变换DWT(Discrete Cosine Transform)、傅里叶变换FT(Fourier Transform)、离散小波变换DWT(Discrete Wavelet Transform)等方法将图像转变到时频，产生混沌随机序列，通过对得到的频域子带，实施加密处理[12-15]。这种利用两类加密方法同时设计加密算法，不仅可以提升算法的效率与安全性，而且降低加密的数据量，获得无损解密图像，这对实时性要求较高的医疗、遥感、军事等领域具有较高的使用价值。

由上述分析，本文将SCAN方法与二维离散小波相结合，设计了一种新颖的无损加密方案。先将图像划分为若干个子块，利用混沌系统产生混沌序列对子块置乱和扩散；再通过DWT将图像转化到频域，并对各个子带进行置乱；最后利用IDWT将图像数据转化到空域，得到密文图像。

1 相关知识

1.1 二维离散小波变换

二维离散小波变换是一种将信号进行分解和压缩的频域处理技术，是现代数字信号处理领域不可缺少的。二维离散小波变换因其具有多分辨率、局部时频特性、频率压缩特性，使得其在图像编码、图像处理、图像压缩等领域得到广泛的应用。二维离散小波变换的核心工作原理是[12]：首先对输入的信号源LL0按行做小波分解，然后按列对获取到的中间数据再做小波分解。对输入的信号源LL0，一级离散小波变换后，信号源划分成四个子带：低频子带(LL1)和高频子带(HL1、LH1、HH1)。如：对低频子带LL1继续执行离散小波变换，可得到四个子带LL2、HL2、LH2、HH2，对低频子带连续执行n次类似的操作，就可获得n级变换的结果，将分解的子带进行IDWT可以实现对图像得重构，得到原始图像[7]。LL是水平方向的低通滤波器，HH是垂直方向的高通滤波器，HL和LH子带是通过在一个方向上的低通滤波，并在另一个方向上高通滤波得到的。子带系数在LL中数值是最大，被称为近似图像，保留着原始图像信息，而且能够分辨出明文的轮廓与细节特征，图像的加密大多在近似子带中进行。

离散小波变换含多类小波转换方法，包含Haar、Daubechies、Meyer小波转换等。其中，Haar小波转换是最简单的一种转换，对图像不会造成信息丢失，是一种无损的变换。

1.2 SCAN方法

SCAN代表的是基于形式语言的二维空间扫描方法，主要用于图像压缩、加密、数据隐藏等，以便表示和生成众多的扫描路径[16]。SCAN系列的形式语言包括几个版本，如Simple SCAN、Extended SCAN、Generated SCAN等，每种都可以表示和生成一组特定的扫描路径。每种语言都具有一组基本的扫描模式，一组变换和一组可以组成简单扫描模式的规则，为了得到较为复杂的扫描路径，通常用几种扫描路径进行组合，得到复杂的扰乱模式。SCAN方法的基本思想就是：通过将像素打乱来重排图像像素，重排是由已定义的SCAN语言的扫描路径实现的。

SCAN语言形式上用语法表示为G=(Γ,Σ,A,Π)，式中：Γ={A,S,P,U,T,V}是非结尾符号；Σ={c,d,o,s,r,a,em,y,w,b,z,x,B,Z,X,(,),space,0,1,2,3,4,5,6,7}是结尾符号；A是起始符号，它在式(1)中被定义；Π是乘积规则。图1表示SCAN算法的基本模式[16]。

A→S|P
S→UT
P→VT(AAAA)
U→c|d|o|s|r|a|e|m|y|w|b|z|x
V→B|Z|X
T→0|1|2|3|4|5|6|7

(1)

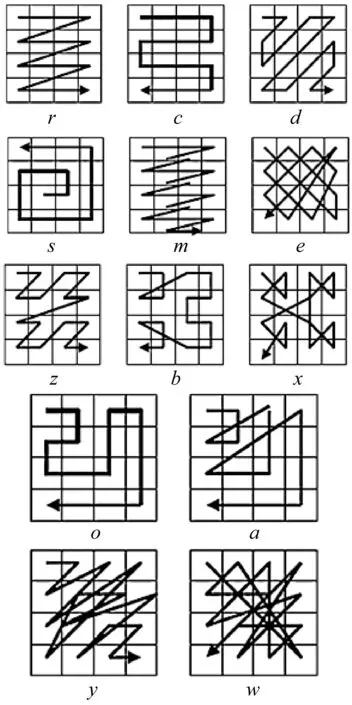
图1 SCAN基本模式

对于扫描，定义为：0是图2的同等变换，2代表顺时针旋转90度。对于如下扫描模式(c，0，s，a，e，m，y，w，b，x)，4和6分别表示图像顺时转旋转180度和270度。对r和z，4表示垂直反射，6表示顺时针旋转90度后再垂直反射，对d，4表示水平反射后顺时针旋转90度，6表示垂直反射后顺时针旋转180度。最后，对于图1中的所有扫描路径，1、3、5、7分别是0、2、4扫描路径的反过程。举个实例：s2是将s扫描路径顺时针旋转90度得到的扫描路径，如图2所示；d表示对角线，7表示6的相反路径，d6表示垂直反射后顺时针旋转180度得到的扫描路径，d7是d6扫描路径的反过程，具体转换过程如图3所示。

图2 s顺时针旋转90度得到s2

1.3 混沌系统

基于混沌系统本身所特有得一些优良特质，使得在密码系统中得到普及，但是随之也产生了一些问题，一些混沌系统无法对抗明文攻击，而且单一的和已知混沌系统被频繁使用，故意破坏者可以掌握一定的规律，破解明文截取密文图像。为了解决这类问题，专家需要设计一些新的混沌系统。

Logistic和Sine混沌系统是已经被广泛使用的一维混沌系统，它们混沌行表现的较为复杂，是一种实现起来比较简单的动力学方程，定义如式下[17-18]：

xi+1=uxi(1-xi)

(2)

(3)

式中：u,a∈(0,4]为系统参数，当xi∈(0,1)，μ∈[3.569 945 6,4]，式(2)、式(3)停留在混沌状态。

本文介绍两种具有简单结构的新型混沌系统，这两个混沌系统已经被证明其混沌范围分布更广[17-18]，即使控制参数超出了一定范围，仍然具有混沌行为。因此其具有优良的混沌和扩散特性，可以抵抗不同类型的攻击，特别是挑选其中一个明文的像素进行攻击。两个混沌系统分别为一维Logistic-Sine与二维Logistic-Adjusted-Sine混沌系统，由一维Logistic和Sine混沌系统组合而成，简称一维Logistic-Sine混沌系统为LSS，二维Logistic-Adjusted-Sine为2D-LASM[17-18]。两个系统的定义如下：

(4)

(5)

在式(4)、式(5)中，当r∈(0,4]，μ∈[0,1]，以上两个系统表现为混沌特性。

2 图像加密算法

为了简便，设彩色明文图像I0的大小为M×N。具体的算法步骤描述如下：

步骤1将明文彩色图像I0进行分离，分别获取三个大小是M×N的矩阵R、G、B。

步骤2随机选取2D-LASM的控制参数u，及初始值x0和y0，对式(5)迭代N0次，用得到的第N0+1次的值作为第二次迭代的初始值。对式(5)迭代MN得到长度为MN的2个混沌序列L1，L2，…，Li，这里Li(j)=xj(i),Li(j)=yj(i)(j=1,2,…,MN)。根据式(6)、式(7)改进与优化混沌序列，获取长度为MN的向量ex1、ex2以及长度为16的序列Lx1、Lx2、Lx3、Lx4。对以上四个向量进行排序，得到四个有序向量Va1、Va2、Va3、Va4。对于向量Lx1、Lx2、Lx3、Lx4中的每个数据，找到其在对应的有序向量中的位置并记录该位置编号，从而得到四个位置序列，四个位置序列减one得到用于SCAN置乱的四个随机序列。

(6)

(7)

式中：mm=12，round(·)为四舍五入的取整函数。

步骤3将大小为M×N的图像分成32个大小为8×8的子块，每个8×8的子块又被划分为16个尺寸为4×4的图像块，每个4×4的图像块分别用步骤2中产生的随机序列进行SCAN置乱操作，得到置乱序列LR。

步骤4设置LSS的初始值和密钥x、r,对变量x、r进行逻辑处理得到混沌系统的初始值，迭代LSS混沌系统M×N+N0次，N0是一个常数，得到混沌序列s。对s进行处理得到分布在[0,255]之间的整数序列，将上述得到的置乱序列转化为二维矩阵Rtemp，进行扩散操作，利用式(8)、式(9)先对矩阵行的像素值进行改变，得到混淆矩阵RC。此次扩散操作分为两部分进行，第二轮扩散操作是对整个RC矩阵进行的，扩散过程是从列方向出发进行的，最终扩散完成后得到矩阵RF。将式(10)得到的扩散矩阵RF转化为一维向量，用前面已经介绍过SCAN算法中定义的两种扫描路径，对图像序列用外螺旋扫描方法s0和对角线扫描方法d7对图像进行进一步的置乱操作，得到经过两轮扰乱操作的二维矩阵PR、PG、PB。

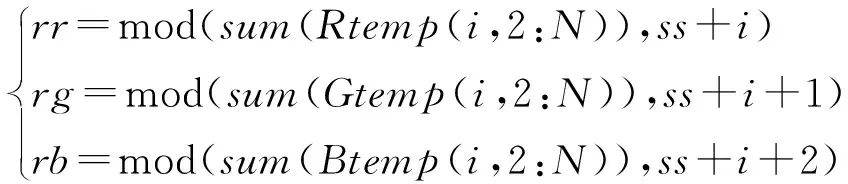
(8)

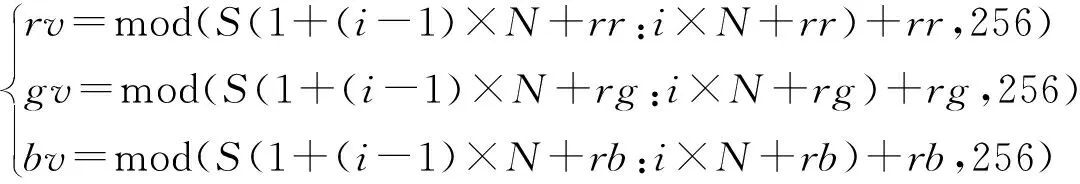
(9)

(10)

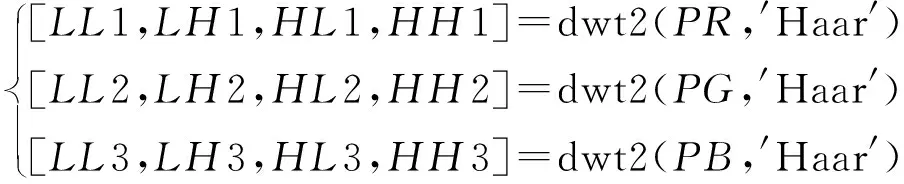
(11)

(12)

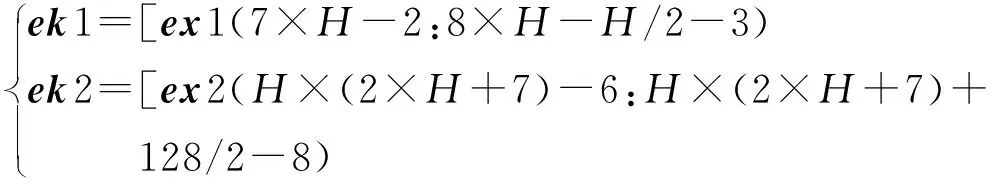
(13)

步骤6利用二维离散小波逆变换，按照如式(14)，将各子带重新转换到空间域，得到最终的加密矩阵C1、C2和C3，为加密图像的三基色图像，从而得到密文图像。

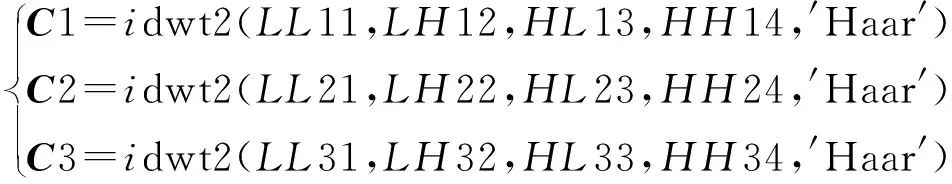
(14)

图像解密算法为图像加密过程的逆过程，对于解密算法只需将加密算法的过程反过来即可解密出原始明文图像。

3 实验结果与分析

图4 Lena图像的加解密图

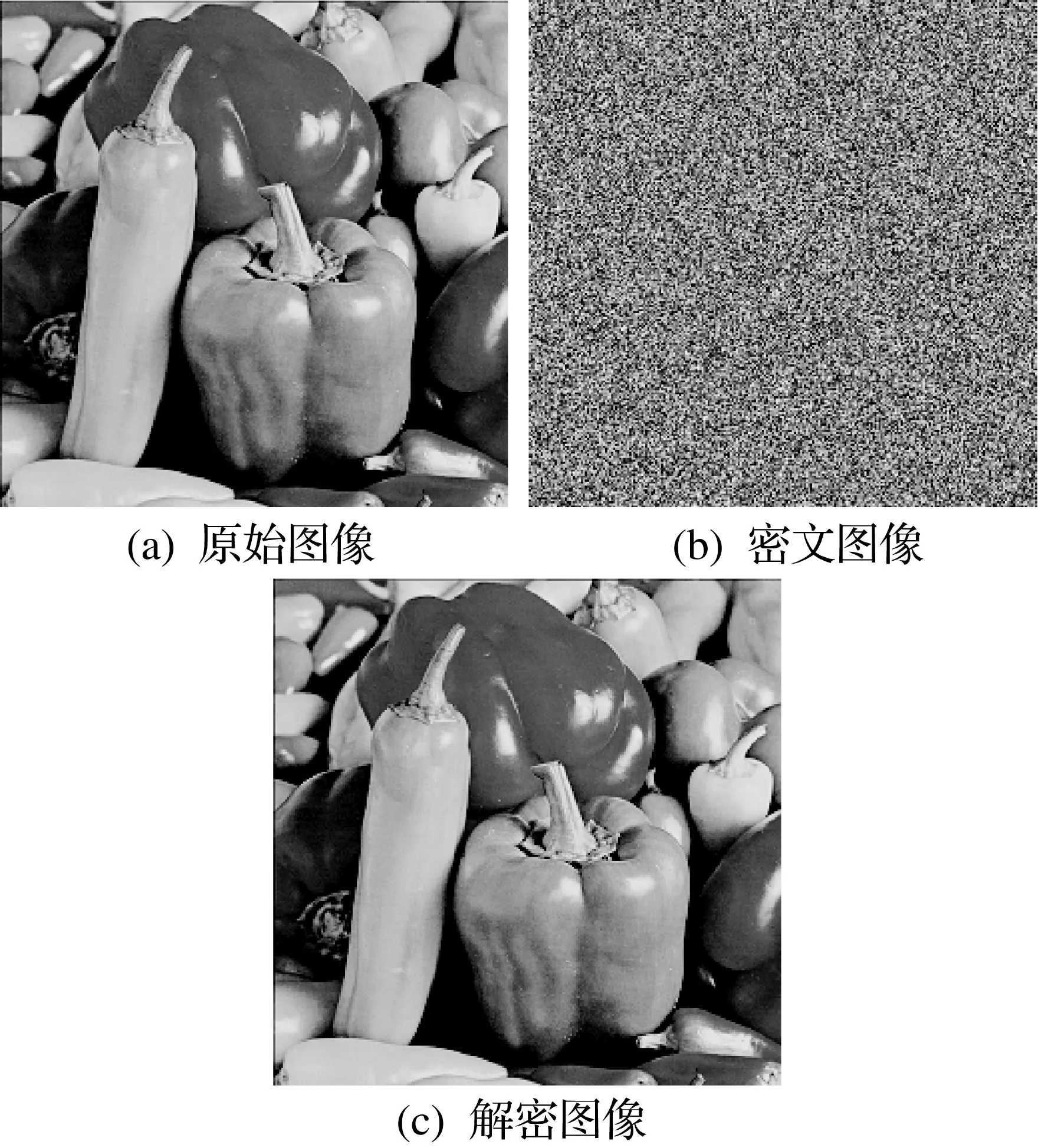
图5 Peppers图像的加解密效果

3.1 敏感性分析

NPCR和UACI是衡量加密算法优良的一个极其重要的指标，一个较好的加密算法应该对密钥以及对密钥做的微小改变极其敏感，NPCR的理想值为100%，UACI的理论值为33.3%，其计算公式如下[19]：

(15)

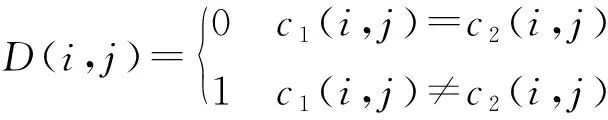
(16)

式中：c1,c2是加密过程中的两个密钥。

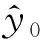
(a) u改变后的解密图像 改动后的解密图像图6 密钥敏感性分析

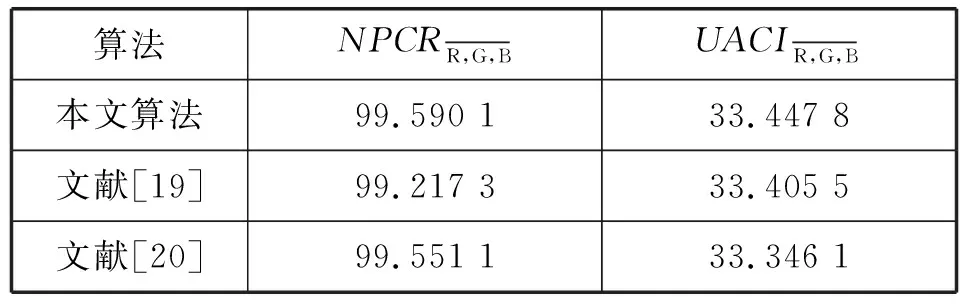
算法NPCRR,G,BUACIR,G,B本文算法99.590 133.447 8文献[19]99.217 333.405 5文献[20]99.551 133.346 1

3.2 直方图分析

图7与图8分别展示了明文图像与密文图像在各分量上的直方图。可以看出，密文图像的分量分布直方图和明文分量分布直方图有明显差异，密文图像的直方图分布较为扁平、均衡，攻击者从密文直方图中不能分析出明文图像的任何特征，很难达到破解明文图像的目的。

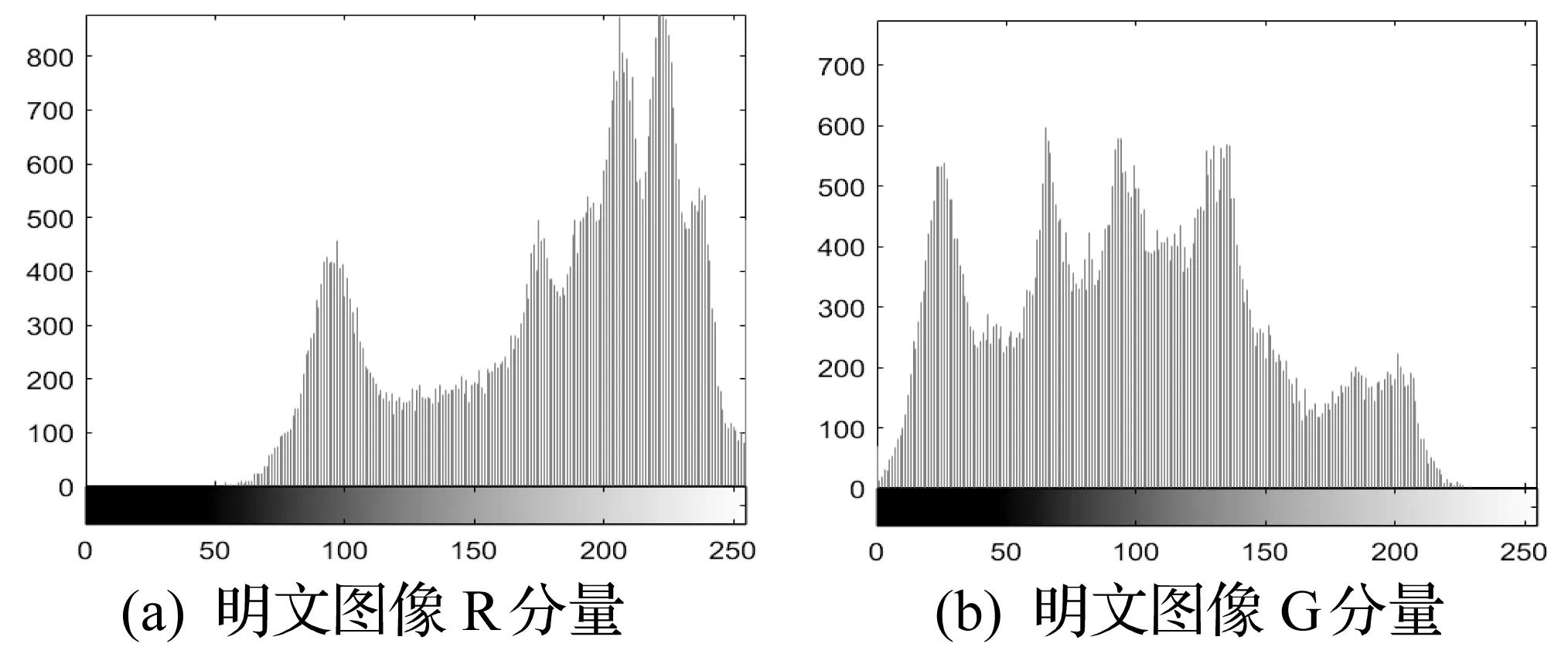
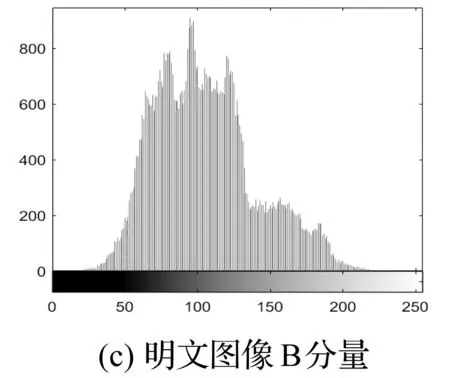
图7 明文R、G、B分量的直方图

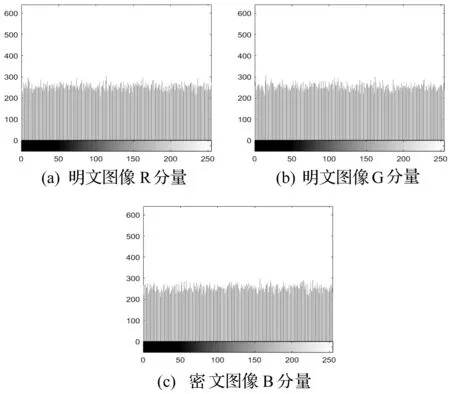
图8 密文R、G、B分量的直方图

3.3 相邻像素相关性分析

图像与其他载体一个明显的区别是：图像像素之间拥有较强的相关性，而且每个像素是相互依赖的。如果设计者想提出一个安全性较高的加密算法，必须尽可能削弱和消除这一现象，以此想法设计的加密算法能够满足密码系统的要求。相关性系数的计算公式如下[21]：

(17)

(18)

(19)

(20)

式中:x、y分别表示图像中两相邻像素的灰度值，cov(x,y)为协方差，D(x)和E(x)分别表示方差和均值。

为了计算明文图像和密文图像的相关性系数，我们分别在不同的方向上随机选取3 000个相邻像素。图9和图10分别展示了明文图像与密文图像在R、G、B分量上相邻像素点之间的相关性。图中可以明显观察到，直线上密集分布着明文图像像素值，对密文图像的相邻像素，其呈现杂乱分布，无规律性可寻。从表2中观察到，明文图像相邻像素的相关系数值仅次于1，相关性极高，相反，密文图像的相关系数值呈现负数分布，联系较低。表3列举了使用本加密算法和文献[3，22]的算法得到的密文图像相邻像素相关系之间的比较。由表3得出，使用本加密算法得到的密文图像的相关系数整体较文献[3，22]的算法所得到的密文图像的相关系数小，因此在弱化相邻像素间的相关性过程中此加密算法具有优良的加密效果。

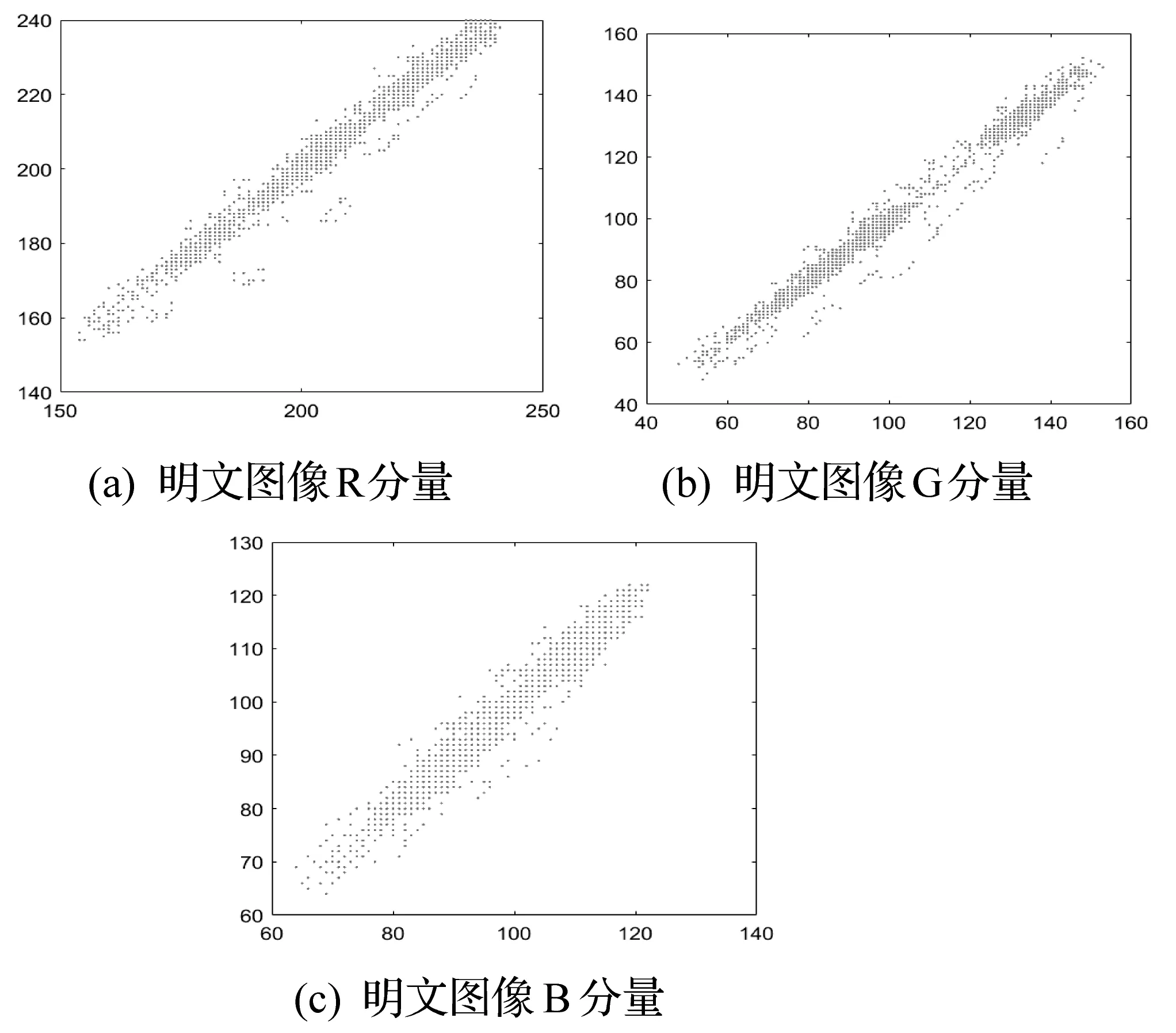
图9 原图相关性

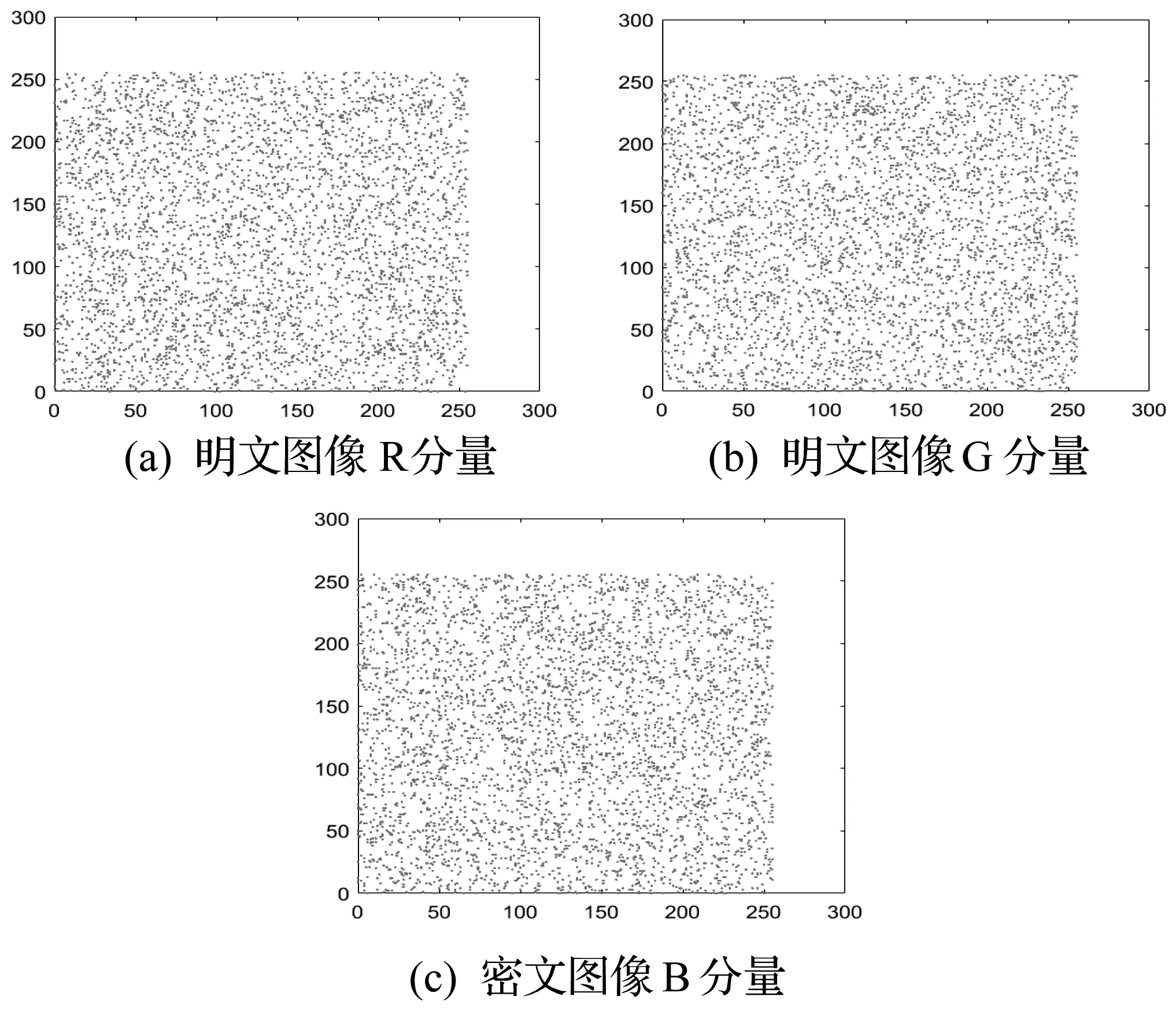
图10 密文相关性

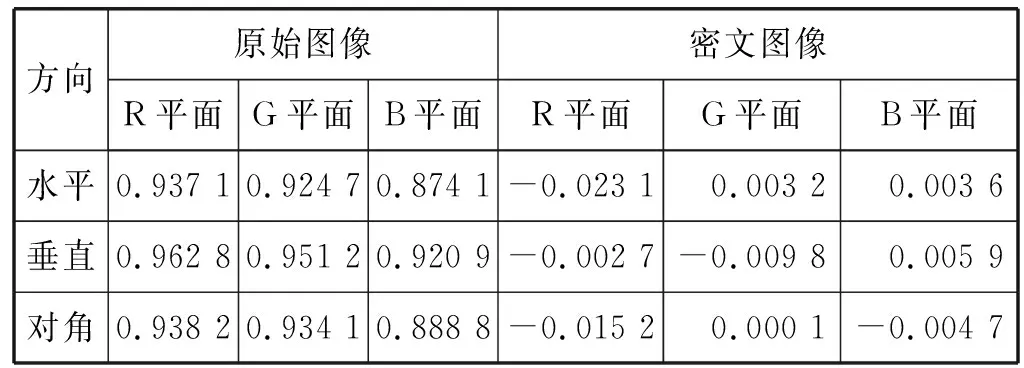
方向原始图像密文图像R平面G平面B平面R平面G平面B平面水平0.937 10.924 70.874 1-0.023 10.003 20.003 6垂直0.962 80.951 20.920 9-0.002 7-0.009 80.005 9对角0.938 20.934 10.888 8-0.015 20.000 1-0.004 7

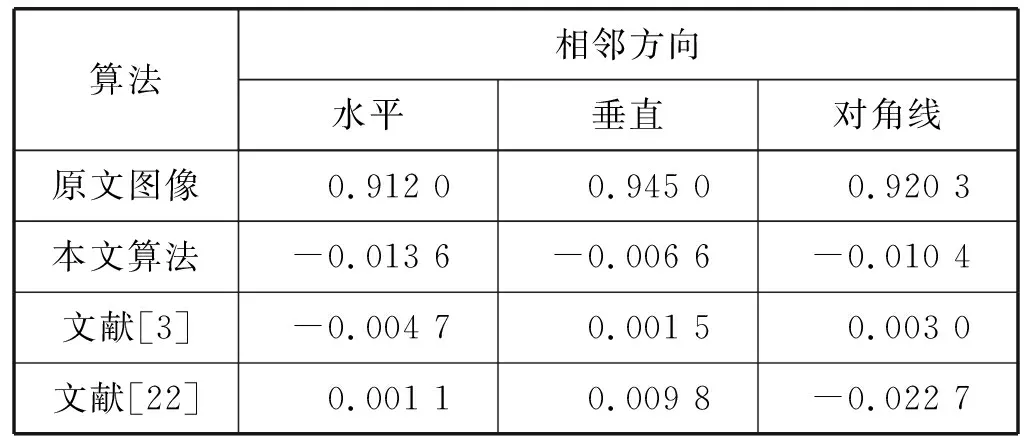
表3 不同加密算法像素相关性之间的比较

3.4 信息熵分析

为了解决对信息的量化度量问题，香农提出了信息熵这个概念，信息熵主要用来描述信源的不确定度，其表示的是图像中灰度值的分散状态。信息熵越大，表明图像中像素值之间的差值越小，反之，信息熵越小。信息熵的理想值是8，若计算结果向理想值逼近，说明加密效果能达到理想得效果。信息熵的计算公式如下：

(21)

式中:x表示图像像素值，P(xi)为xi出现的概率。

文中实验采用标准的Lena彩色图像为测试图，表4不仅列出了本加密算法密文图像各分量的信息熵，而且还与其他加密算法做了对比。从表中数据观察到，此加密算法的信息熵最接近理论值8。此分析表明密文图像的像素值呈现等概率出现的现象。

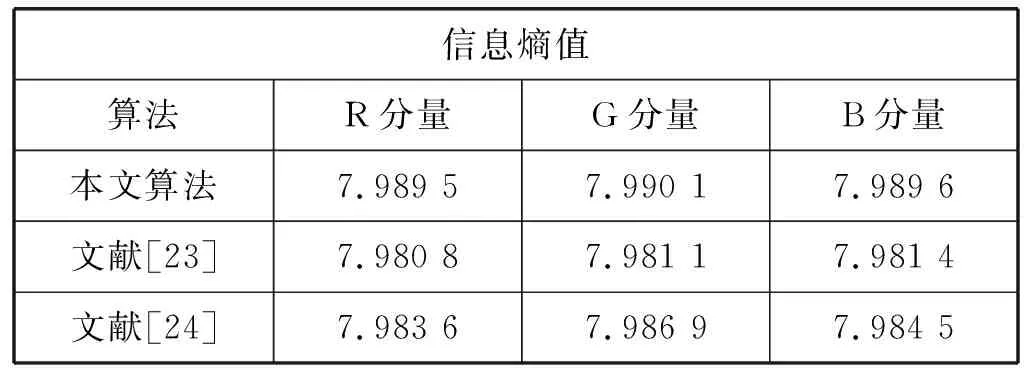
表4 不同加密算法之间信息熵的对比

4 结 语

本文将SCAN方法和二维离散小波变换相结合，并利用两种新的混沌系统LSS和2D-LASM系统用于扩散和置乱操作，产生的随机序列作为SCAN方法的扫描路径，将扫描路径随机化，增加了算法的安全性和抗攻击性；利用二维离散小波变换将图像从空域变换到频域，得到四个子带，利用混沌序列对子带进行置乱后，进行逆二维离散小波变换得到最终的密文图像。实验结果表明，本文提出加密算法计算速度快，密钥空间大，像素相关性低，能够有效抵抗攻击，安全性比较高，适用于各种数字图像加密。