浅海Scholte波的频散特性研究
2018-09-26罗夏云程广利张明敏刘雁春
罗夏云, 程广利, 张明敏, 刘雁春
(1.海军工程大学 电子工程学院, 湖北 武汉 430033; 2.海军工程大学 导航工程系, 湖北 武汉 430033)
0 引言
由舰艇发出的甚低频声场及水压场与海底的频繁接触导致能量传入海底,诱发了海底介质中横波、纵波、表面波等多种振动波。其中,沿海底表面传播的地震波是一种在波动方式上不同于水中声波的固体表面波,称为Scholte波。其在界面处具有幅度大、频率低、传播距离远的特点,传播速度不会因季节、气象水文条件而改变,更不会像声波那样受到海水介质起伏和内波等随机因素的干扰,同时也与声波一样携带着目标的位置信息[1-2],因此Scholte波可作为海底振动传感器的地声探测信号,并在水雷引信和水下目标探测等方面具有重要的应用价值[3]。
Scholte波相速度是获取目标位置信息的关键参数,同时也能利用其反演海底剪切波速度剖面[4],但是因为Scholte波在传播过程中,不同频率向海底渗透能量的深度不同,存在相速度随频率变化的频散现象,所以像传统方法那样利用阵列的阵间距与信号到达各阵元相对时延差的比值求取Scholte波相速度与实际情况是不相符的,因此确定Scholte波的频散特性,对Scholte波速度场、时空特性、目标定位、海底参数反演等方面的研究具有重要意义。
针对表面波频散问题,各国学者主要从频散理论[5-8]、提取方法[9-13]、试验分析[14-17]等方面展开了研究。频散理论方面,文献[5]推导了Scholte波相速度频散方程,认为当雷诺数大于2 500时可以忽略流体黏性对Scholte波相速度的影响。文献[6]采用复变函数方法推导求解液体与固体半无限空间分界面上Scholte波的频散方程,并证明了如果Scholte波存在,那么一定是唯一的。文献[7]建立了含沉积层的半无限弹性海底模型,仿真分析了海底沉积层对Scholte波频散特性的影响,结果表明覆盖在硬海底上的软沉积层对Scholte波频散特性影响最大,且高频率成分在沉积层中衰减大。文献[8]建立了分层海底模型,研究发现Scholte波受海底介质中横波速度影响最大,频散曲线的转折点可用于估算弹性沉积层厚度。
国外学者较早地开展了Scholte波频散曲线提取方法的研究。1968年Landisman等[9]提出采用滑动窗分析法分析地震引发的海底地震波的频散特性,1969年他又提出一种快速、有效地分析频散特性的方法——多重滤波技术[10],此方法相比滑动窗分析法具有更高的频率分辨率,但是在信噪比较低或者信号波形发生混叠的情况下效果较差。1981年McMechan等[11]采用频率波数谱方法提取Scholte波相速度频散曲线。1998年Mallat等[12]利用小波变换法提取群速度频散曲线,该方法具有较高的频率分辨率。2012年Potty等[13]采用动态刚度矩阵建模仿真并分析了Scholte波的频散特性。但国内则鲜有这方面的研究文献。
国外关于地震波频散的试验研究主要集中在地球物理和地球物理勘探方面,只有少部分文献针对海底Scholte波频散特性展开研究。文献[14]在深海中进行了爆炸声激发Scholte波的接收试验,采用滑动窗分析法分析Scholte波的频散特性,结果表明爆炸点与传感器之间的距离小于1 250 m时,Scholte波存在明显的频散现象,而距离在2 100 m左右时不能有效地判别出Scholte波信号。文献[15]在美国俄勒冈州海岸和圣地亚哥海岸进行了爆炸声激发Scholte波的接收试验,试验分析结果表明两个试验地点接收到的Scholte波在不同频段均存在频散特性。在国内,张海刚[16]利用近岸的地震波测量系统进行了目标船航行辐射噪声激发地震波测量试验;卢再华等[17]在汉江上开展了9个批次的实船地震波检测试验;李响等通过试验在目标定位[18]、地震波场[19]等方面展开了研究。文献[16-19]都只是在试验中观察到了Scholte波,没有讨论Scholte波的频散问题,同时在试验过程中将地震检波器布放在岸上而非海底,导致接收到的信号是Scholte波从海底传播到岸上发生波型转换后的信号。
综上所述,目前国内外主要通过理论分析、建模仿真的方法研究Scholte波的频散特性,而针对浅海中声源激发的地震波试验研究相对较少,使得基于这类试验数据研究Scholte波频散特性的文献就更少。
本文以半无限海底声场模型为对象,基于波动理论推导Scholte波的频散方程,仿真分析了两种典型弹性固态海底条件下Scholte波的频散特性;组织开展了湖上气枪声源激发的地震波试验,利用布放于湖底的地声传感器阵列接收信号,采用文献[9]提出的滑动窗分析法研究了Scholte波频散特性。试验分析与理论仿真结论相一致,表明所建模型及其理论分析的正确性,同时证明了滑动窗分析方法也适用于分析浅海声源所激发出的Scholte波频散特性,为Scholte波速度场、时空特性、目标定位、海底参数反演等方面的研究奠定了基础。
1 海底地震波理论
建立如图1所示的半无限弹性海底模型,上层介质是厚度为H、密度为ρ1、声速为c1的均匀流体层,下层介质是密度为ρ2、横波速度为cs、纵波速度为cp各向同性的半无限弹性海底,上下层介质均为理想介质。取柱坐标系,声源为单频点声源,位于z轴上,深度为z0,r轴代表水平方向距离,z轴代表垂直方向距离.
φ1、φ2、ψ2分别为流体层纵波、海底纵波以及海底横波的位移势函数,满足以下波动方程:
(1)
设u、v分别为水平位移和垂直位移,pzz、pzr分别为法向应力和切向应力,λ和μ分别为拉梅系数,则位移、应力与势函数存在以下关系[14]:
(2)
式中:下角标1代表在液体层中;下角标2代表在弹性海底中。
在液体层表面(z=0)、点源处(z=z0)以及液体与固体分界面(z=H)分别满足以下边界条件:
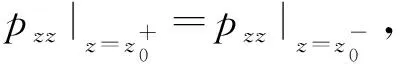
(3)
考虑到各势函数满足z=0处边界条件以及无穷远处辐射条件,则(1)式中各势函数的通解可写为
(4)
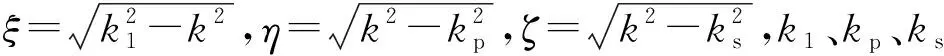
根据点源条件及分界面的边界条件,可得各待定系数所应满足的方程为
(5)
整理后可以得到各待定系数的分母项为
(6)
(6)式也可写为
(7)
(7)式即为Scholte波的特征方程。
将k1、kp、ks和分离常量代入(7)式中可得
(8)
(8)式与文献[20]中给出的Scholte波特征方程相同。当特征方程存在实数根时,该实数根即为Scholte波波速。
对特征方程(7)式作如下讨论:


2 滑动窗分析算法
本文采用Dziewonski提出的滑动窗分析方法分析Scholte波频散特性。滑动窗为矩形窗,窗长随信号周期而变化,以期在信号所有的周期上都能保持相同的频率分辨率。具体算法如图2所示,步骤如下:
1)设计矩形窗参数。d为声源与阵元之间的距离, 给定群速度v以及周期T的取值范围,vn、Tm分别为在给定的群速度与周期范围内第n点的群速度以及第m点的周期取值,W为矩形窗长度与信号周期的比值。W的取值对数据处理的结果影响较大,Pfeffer等[21]证明了W的取值一般为4~6,本文取W=4.
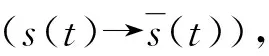
4)对调制后的时间信号进行傅里叶变换后求和,然后取绝对值得到幅度矩阵Anm.
3 数值算例及分析
针对(8)式实数根存在条件,分以下两种情况讨论。
3.1 软海底(cs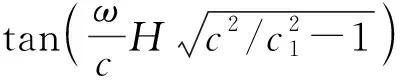
(9)
(10)
表1给出了两种浅海层典型弹性固态海底物质的地声特性,以白垩岩为例,将其参数代入(10)式可得
(11)
式中:f为频率。

表1 浅海层典型弹性固态海底物质的地声特性
在x≥1区间,给定不同的fH值,P(x)随x的增加呈单调递减(见图3),因此在海水深度H给定情况下,每个频率值对应1个实数根。
3.2 硬海底(cs>c1)
当cp>cs>c>c1时,(8)式等号两侧均为纯虚数,存在实数根。以表1中白垩岩为例,将其参数代入(10)式可得
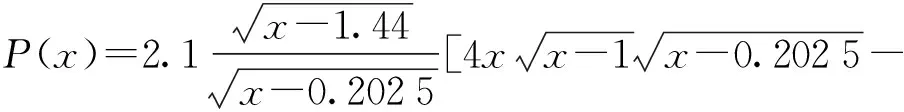
(12)
在x≥1.44区间,给定不同的fH值,在海水深度为固定值时,当频率大于某一数值后P(x)随x的增加呈单调递减(见图4),每个频率值对应1个实数根,而当频率小于这一数值时方程无解,故此条件下Scholte波存在截止频率。
当cp>cs>c1>c时,(8)式等号两侧均为纯虚数,存在实数根,此时方程可变换为以下形式:

(13)
综上分析可知:当海底为软海底时,存在一种海底表面波,即Scholte波;当海底为硬海底时分为两种情况,当c>c1时仅存在Scholte波,当c将表1中粉砂- 黏土、白垩岩参数代入(7)式中,可得到Scholte波频散曲线(见图5)。从图5中可以看出,Scholte波存在频散现象,当声源频率接近0时,Scholte波速度接近于Rayleigh波速度。
4 试验环境概况及气枪布放
试验地点选择在某处地形相对较平坦、环境噪声较小的水库。试验采用一条具有6个垂直轴向压电式振动传感器的线列阵接收数据,阵元间距为55 m. 为了保证阵列沉底后得到理想的均匀线列阵,在布放线缆时,首先将粗线缆在岸边有序排放,在粗线缆的头部和每个阵元处绑上浮球,然后由拖曳船以低速拖向湖中,以此来布放粗线缆和传感器,确保线缆尽量拉直后依次剪掉系浮球的绳子,粗线缆和传感器一并沉入湖底。为获取各阵元精确的空间关系,采用2次定位精确测定各阵元沉底后的位置(见图6),从阵元1到阵元6,相邻两阵元的间距依次为53.6 m、54.2 m、54.1 m、52.8 m、53.0 m.
表2给出了各阵元的深度。试验中选择气枪作为脉冲声源,气枪声源吊放在阵列的端射方向水下6 m处,距阵首端(阵元1)的水平距离为254 m. 试验中气枪发射8 MPa、10 MPa的气压,在气枪声源正上方1 m处悬挂水听器,用以记录气枪子波信号。图7给出了气枪子波发射信号的波形。

表2 阵元深度
5 试验数据处理与分析
图8给出了6个阵元接收的时间信号,图9单独给出阵元1接收到的信号。从图8可以看出,每个阵元信号明显存在时间延迟。根据各阵元的空间相对位置以及每个阵元接收信号的最强幅值时延差,可以计算出幅值最强信号的传播速度约为1 490 m/s. 由于阵元距声源较近,水声信号能量较强,除了能够看到微弱的初至波(即侧面波,以海底纵波的速度传播,速度为2 477 m/s)信号,其他信号均被水声信号淹没。利用小波变换对阵元1接收到的信号进行时频分析,如图10所示,可见信号能量主要集中在50 Hz以上和25 Hz以下这两个频段。对比图9、图10可以看出,图9中幅度最强的信号与图10中50 Hz以上的信号在时间上相对应,再结合此频段信号传播速度为1 490 m/s的特征,可以确定50 Hz以上频带为水声信号。采用截止频率为25 Hz的低通滤波器对阵元1接收到的信号进行滤波,利用小波变换对滤波后信号进行时频分析,结果如图11所示。
针对阵元1和阵元2接收到的信号,采用滑动窗分析方法分别对滤波前、滤波后的信号进行频散分析,得到结果如图12所示。由图12可见,滤波前频率50 Hz以上的水声信号,群速度200~400 m/s之间,与其相速度存在明显差别,这是因为在近距离上,强烈的气枪冲击信号产生的非线性效应所致。滤波后可见10 Hz以下频段明显存在频散现象;5~10 Hz之间群速度随频率的增加而减小;频率高于10 Hz后,随着频率增加群速度基本保持不变;变化规律与仿真结果相符。
为确定地震波相速度,选取频散现象不明显的频带,采用10~15 Hz的带通滤波器分别对阵元1~阵元6接收气枪压力8 MPa和10 MPa激发的信号进行滤波,并对滤波前、滤波后的信号进行归一化处理,结果如图13、图14所示,图中黑线代表滤波前时域信号,红线代表滤波后时域信号。根据阵元间距及相对时延,其中幅度最大的波系其相速度分别为422.9 m/s、422.7 m/s. 由此可见,该波系属于地震波中的Scholte波。
6 结论
为了研究浅海中Scholte波的频散特性,本文建立了半无限弹性海底模型,开展了湖上气枪声源激发的地震波试验。所得主要结论如下:
1)理想半无限固态弹性海底模型下,不同海底条件下均能激发产生Scholte波,且存在频散现象。 2)利用滑动窗分析方法对湖上试验数据展开分析,结果表明,Scholte波存在频散特性,试验分析与理论仿真结果的频散规律一致,说明滑动窗分析方法适用于分析浅海声源所激发出的Scholte波频散特性。
3)针对Scholte频散特性,分别对8 MPa、10 MPa气枪压力下阵元接收的时域信号进行10~15 Hz带通滤波,根据阵元间距及相对时延差计算得到试验水域的Scholte波相速度约为422 m/s.
本文主要针对此次湖上试验数据分析了Scholte波频散特性,声源深度变化、距离变化、海水层厚度以及不同海底物质的地声特性等对Scholte波频散特性影响,有待于进一步研究。
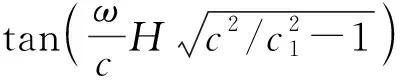
(9)
(10)
表1给出了两种浅海层典型弹性固态海底物质的地声特性,以白垩岩为例,将其参数代入(10)式可得
(11)
式中:f为频率。

表1 浅海层典型弹性固态海底物质的地声特性
在x≥1区间,给定不同的fH值,P(x)随x的增加呈单调递减(见图3),因此在海水深度H给定情况下,每个频率值对应1个实数根。
3.2 硬海底(cs>c1)
当cp>cs>c>c1时,(8)式等号两侧均为纯虚数,存在实数根。以表1中白垩岩为例,将其参数代入(10)式可得
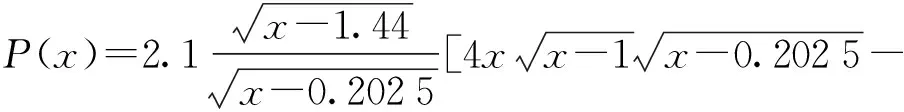
(12)
在x≥1.44区间,给定不同的fH值,在海水深度为固定值时,当频率大于某一数值后P(x)随x的增加呈单调递减(见图4),每个频率值对应1个实数根,而当频率小于这一数值时方程无解,故此条件下Scholte波存在截止频率。
当cp>cs>c1>c时,(8)式等号两侧均为纯虚数,存在实数根,此时方程可变换为以下形式:

(13)
综上分析可知:当海底为软海底时,存在一种海底表面波,即Scholte波;当海底为硬海底时分为两种情况,当c>c1时仅存在Scholte波,当c 将表1中粉砂- 黏土、白垩岩参数代入(7)式中,可得到Scholte波频散曲线(见图5)。从图5中可以看出,Scholte波存在频散现象,当声源频率接近0时,Scholte波速度接近于Rayleigh波速度。 试验地点选择在某处地形相对较平坦、环境噪声较小的水库。试验采用一条具有6个垂直轴向压电式振动传感器的线列阵接收数据,阵元间距为55 m. 为了保证阵列沉底后得到理想的均匀线列阵,在布放线缆时,首先将粗线缆在岸边有序排放,在粗线缆的头部和每个阵元处绑上浮球,然后由拖曳船以低速拖向湖中,以此来布放粗线缆和传感器,确保线缆尽量拉直后依次剪掉系浮球的绳子,粗线缆和传感器一并沉入湖底。为获取各阵元精确的空间关系,采用2次定位精确测定各阵元沉底后的位置(见图6),从阵元1到阵元6,相邻两阵元的间距依次为53.6 m、54.2 m、54.1 m、52.8 m、53.0 m. 表2给出了各阵元的深度。试验中选择气枪作为脉冲声源,气枪声源吊放在阵列的端射方向水下6 m处,距阵首端(阵元1)的水平距离为254 m. 试验中气枪发射8 MPa、10 MPa的气压,在气枪声源正上方1 m处悬挂水听器,用以记录气枪子波信号。图7给出了气枪子波发射信号的波形。 表2 阵元深度 图8给出了6个阵元接收的时间信号,图9单独给出阵元1接收到的信号。从图8可以看出,每个阵元信号明显存在时间延迟。根据各阵元的空间相对位置以及每个阵元接收信号的最强幅值时延差,可以计算出幅值最强信号的传播速度约为1 490 m/s. 由于阵元距声源较近,水声信号能量较强,除了能够看到微弱的初至波(即侧面波,以海底纵波的速度传播,速度为2 477 m/s)信号,其他信号均被水声信号淹没。利用小波变换对阵元1接收到的信号进行时频分析,如图10所示,可见信号能量主要集中在50 Hz以上和25 Hz以下这两个频段。对比图9、图10可以看出,图9中幅度最强的信号与图10中50 Hz以上的信号在时间上相对应,再结合此频段信号传播速度为1 490 m/s的特征,可以确定50 Hz以上频带为水声信号。采用截止频率为25 Hz的低通滤波器对阵元1接收到的信号进行滤波,利用小波变换对滤波后信号进行时频分析,结果如图11所示。 针对阵元1和阵元2接收到的信号,采用滑动窗分析方法分别对滤波前、滤波后的信号进行频散分析,得到结果如图12所示。由图12可见,滤波前频率50 Hz以上的水声信号,群速度200~400 m/s之间,与其相速度存在明显差别,这是因为在近距离上,强烈的气枪冲击信号产生的非线性效应所致。滤波后可见10 Hz以下频段明显存在频散现象;5~10 Hz之间群速度随频率的增加而减小;频率高于10 Hz后,随着频率增加群速度基本保持不变;变化规律与仿真结果相符。 为确定地震波相速度,选取频散现象不明显的频带,采用10~15 Hz的带通滤波器分别对阵元1~阵元6接收气枪压力8 MPa和10 MPa激发的信号进行滤波,并对滤波前、滤波后的信号进行归一化处理,结果如图13、图14所示,图中黑线代表滤波前时域信号,红线代表滤波后时域信号。根据阵元间距及相对时延,其中幅度最大的波系其相速度分别为422.9 m/s、422.7 m/s. 由此可见,该波系属于地震波中的Scholte波。 为了研究浅海中Scholte波的频散特性,本文建立了半无限弹性海底模型,开展了湖上气枪声源激发的地震波试验。所得主要结论如下: 1)理想半无限固态弹性海底模型下,不同海底条件下均能激发产生Scholte波,且存在频散现象。 2)利用滑动窗分析方法对湖上试验数据展开分析,结果表明,Scholte波存在频散特性,试验分析与理论仿真结果的频散规律一致,说明滑动窗分析方法适用于分析浅海声源所激发出的Scholte波频散特性。 3)针对Scholte频散特性,分别对8 MPa、10 MPa气枪压力下阵元接收的时域信号进行10~15 Hz带通滤波,根据阵元间距及相对时延差计算得到试验水域的Scholte波相速度约为422 m/s. 本文主要针对此次湖上试验数据分析了Scholte波频散特性,声源深度变化、距离变化、海水层厚度以及不同海底物质的地声特性等对Scholte波频散特性影响,有待于进一步研究。4 试验环境概况及气枪布放

5 试验数据处理与分析
6 结论
