基于改进无迹卡尔曼滤波的弹道射程修正算法研究

雷晓云， 张志安， 杜忠华

(南京理工大学 机械工程学院， 江苏 南京 210094)

0 引言

基于全球定位系统(GPS)的弹道射程修正弹(即一维弹道修正弹)首先对GPS测量值进行预处理，再将处理后的数据作为弹道控制算法的解算基础，提供给初始弹道诸元。最常用的预处理算法是扩展卡尔曼滤波(EKF)最优估计[1]，该方法能有效地降低GPS测量误差，虽然相对于原始未经滤波的弹道数据而言，预测误差有明显降低，但是由于模型简单，对于具有高精度要求的弹道射程修正弹仍不能满足其要求。此外，EKF的状态转移矩阵复杂化，计算过程涉及的参数较多，参量摄动和状态突变会使滤波过程发散，稳定性相对不高。文献[2]提出采用序列最小二乘法对小数量数据样本进行处理，获得了相对于原数据而言更高精度的数据。文献[3]采用小波变换原理对不同误差进行处理，该方法对消除观测噪声具有很好的效果。文献[4]结合递归最小二乘方法和EKF估计器辨识再入飞行器的轨道。文献[5-9]均表明非线性处理方法在GPS数据处理上的应用非常常见。

本文根据基于GPS的弹道射程修正弹基本修正原理和牛顿插值原理，重新估计具有粗大误差的测量数据，以此改进无迹卡尔曼滤波(UKF)算法，用以预处理GPS测量数据，降低异常测量值和定位失锁情况对滤波效果的影响，并将改进后的UKF算法融入至提出的弹道修正控制算法中。根据仿真分析确定最优修正效果的滤波参数选择原则，并从射击试验分析的角度验证基于改进UKF算法的射程修正算法在降低GPS测量误差对修正射程精度影响中的实际可行性，为工程应用提供一定的参考。

1 弹道射程修正控制算法

本文建立的三维质点弹道模型如(1)式所示：

(1)

根据弹道射程修正弹的基本修正原理，可采用如下计算修正时刻(即阻力片张开时刻)的算法，其基本原理如图1所示。图1中，A、B、C、D表示4条修正弹道轨迹，E表示无控弹道轨迹，轨迹上标记的0、1、2、3、4、5分别表示5组不同修正时刻。

在GPS测量数据无误差的理想条件下，从弹丸上升初始阶段选择一组GPS数据作为弹道解算的初始条件，以该条件预测无控弹道轨迹E，此时即可通过数值积分算法估算出飞行剩余时间T. 考虑分散性，将初始条件时刻作为相对起始时刻0，选择修正时刻分别为0、T/4、T/2以及3T/4时刻，估算修正弹道轨迹A、B、C、D. 按弹道预测的顺序进行弹道解算，首先计算未修正弹道，当遇到修正时刻点时停止当前计算，转而开始计算修正弹道，计算完成后返回停滞点继续计算未修正弹道。由于最后一个修正时刻点无需计算，该过程一共需要暂停4次，在计算未修正弹道的同时，其他4条修正弹道也被计算出来。

至此，5组修正时刻与修正量数据组均已确定，记为(tci,Δxci)，i=0,1,2,3,4，则对于任意修正量Δx(t)，采用牛顿j次插值多项式可得到如下表达式：

Δx(t)=b0+b1(t-tc1)+…+
bj(t-tc1)(t-tc2)(t-tc3)…(t-tcj),

(2)

式中，各阶有限差商就是对应的系数bj，

通过(2)式可以确定一个修正时刻与修正量之间的关系式，即Δx(t)=f(t)，f(t)为(2)式等式右边的函数式，当已知需要修正的射程量Δx时，令Δx-f(t)=0，采用二分法求自变量t即对应修正量的修正时刻。

2 GPS测量误差对修正精度的影响

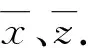
(3)

式中：xi、zi分别为第i次射击的纵向射程和横向射程；m为总的射击次数。本文研究的射程修正弹，只考虑纵向射程的射击精度xi.

精确称取自制的花色苷产品0.1 g，用pH 1.0氯化钾缓冲液稀释至100 mL，再吸取10 mL，用氯化钾缓冲液稀释至 100 mL，在最大吸收波长处测定其吸光值，计算公式为：

GPS动态测量数据包含来自信号传播过程、信号接收过程等方面的误差[12]，本文采用的一种高动态接收机可抗过载50g以上，其水平定位精度为4 m，垂直定位精度为5 m，水平测速精度和垂直测速精度均为0.5 m/s，精度因子PDOP值小于3. 因为分析方法和预处理算法是通用的，所以以该型GPS接收机为例进行讨论。根据误差传播理论可以计算角度精度，假设θa=θa(vx,vy,vz)，ψ2=ψ2(vx,vy,vz)，则由(4)式可计算出角度测量精度，此外在测量过程中还有过程噪声污染数据，因此诸多影响因素会造成测量数据含有较大误差。

(4)

表1 GPS定位误差对修正精度的影响

根据表1可知，在修正能力范围内，相对同一种弹丸来说，Ex值没有明显规律性，Ex与修正射程之间并无明显的关联。表1中的偏差值由修正后的射程与预定射程之间的差值决定，对比两种弹型在不同目标射程下的偏差值可以看出：榴弹的射程均值偏差相对于火箭弹来说更大，最大偏差值达到-13.1 m，最小值-5.1 m；而新40管火箭弹最大射程均值偏差值为4.6 m，最小值-1.5 m. 这说明对于不同的弹丸类型，GPS测量误差对大射程弹丸的修正射程均值偏差影响更明显，对Ex的影响也较大。仿真过程中，随机选取测量数据中的某一组数据作为基本解算条件，如果这一条件与实际情况偏差很大，将会直接影响弹道轨迹预测的准确性。因此，GPS测量数据作为算法的初始条件，对落点精度的影响不可忽视。为了降低弹道测量数据的误差，并提高测量数据的利用率，本文采用改进的滤波方法对GPS测量数据进行预处理，然后再确定弹道解算的基本条件。

3 基于UKF算法的弹道射程修正算法

3.1 改进UKF预处理GPS数据的基本原理

较为常见的弹道数据处理方法是EKF[13]，而相比于EKF，UKF具有最突出的两个优点：1)具有更高的精度而且更加稳定；2)避免了对非线性系统的线性化近似处理过程。UKF采用无迹变换在估计点附近确定采样点，然后利用这些采样点表示高斯密度近似于状态的概率密度函数，降低了计算负担[13]。本文采用UKF方法来降低GPS接收机接收弹道数据的误差。普通滤波方法在滤波噪声参数合适时可以在一定程度上降低测量误差。但是，在实际应用中，如何选择合理的滤波参数一般是比较困难的，且不论测量噪声和过程噪声的准确获取。如参考文献[14]中所述：测量噪声是一个统计意义上的参数，可理解为对传感器测量数据经过长期的概率统计，得出其测量方差；而过程噪声往往与外界因素相关，如空气、风、阳光等，在一个时变系统中，要准确获取是非常困难的。实际上，针对不同的问题，滤波参数选择的不好，滤波效果会非常差。本文在设定的粗略经验滤波参数基础上，对普通滤波方法改进了状态量更新的条件，避免了定位失锁情况对弹道解算的影响。

非线性弹道方程组可表示为状态空间方程的形式，并有观测方程组：

(5)

式中：X为状态量，其协方差矩阵为P；Z为观测量；W为过程噪声，其相应的协方差矩阵为Q；V为观测噪声，其协方差矩阵为R；k为时间序列；f表示系统的状态方程；h表示观测函数。令状态量X=(x,y,z,v,θa,ψ2)T，观测量Z=(x,y,z,v,θa,ψ2)T，观测量数据为WGS-84坐标系通过坐标变换而得到的站心坐标系[12]中的数据，其中观测量中的v、θa、ψ2是通过对直接测量值即速度分量变换得到的间接观测量，则相应的观测函数h=I6×6，I为单位矩阵。

根据建立的非线性状态空间方程组，改进后的UKF流程见图2，其中：α为控制采样点分布状态的参数，一般取值在1×10-4～1之间；β为非负权系数，对于单变量状态量一般取0，对于高斯分布一般取2；λ为放缩比例参数；n为状态量维数；i表示第i个采样点；w为采样点相应的权值；e为误差常数；h为离散化步长。对算法做如下改进：在更新最优状态量前，比较观测量Z(k+1)和观测量的预测估计值之间的差异，根据二者之间的差异辨识接收的观测值是否具有粗大误差，或是否处于GPS定位失锁的情况。如果估计值与实际观测值之间的偏差大于容忍范围，则Z(k+1)被认为是异常测量值，不能直接参与状态量的估计，这种情况下，根据k-2、k-1和k3个时刻的测量预测值，插值推算出k+1时刻的等效测量值来代替原来具有粗大误差的测量值。常用的插值法有Hermite插值、Lagrange插值、牛顿插值等，其中：Hermite插值适用于要求在某些点处的函数值与原表达式相等且导数值也相等的情况；Lagrange插值属于多项式插值法，可迭代性比较差，计算复杂，每添加1个点，公式需重新计算，使计算量增加。对于本文的解算要求，只要求函数值相等，而牛顿插值法具有承袭性，每增加1个点，无需重复计算公式，故牛顿插值法是针对本文情况的最佳选择。k+1时刻的等效测量值采用(6)式计算，其中a11、a12、a13为插值系数，t(k)表示第k个时间步长。

(6)

通过上述对观测量的改进，可以判别出观测值是否存在粗大误差以及GPS是否处于失锁状态。直观看来，该方法无法处理在初始时刻就出现具有粗大误差的测量值情况，因此在k取为1和2时如果出现具有粗大误差的测量值时，需要另外处理，该种情况下将不对状态量进行更新。如果出炮口后就出现GPS长时间无可用有效GPS测量数据的情况，基于GPS的射程修正弹就失去意义，但仍然可以采用延时修正策略进行弹道修正，本文暂不考虑该情况的发生。

已知接收机在3个坐标方向上的容许标准偏差σx、σy、σz时，状态更新的决定条件可表达为：|Z(k+1)-(k+1|k)|

以新40管火箭弹的弹道为例，假设过程噪声协方差矩阵、测量噪声协方差矩阵以及初始状态协方差矩阵相同，仿真计算弹丸位置在站心坐标系3个坐标分量的误差δx、δy、δz，如图3所示，其中“Ls-Le”表示定位丢失的数据段，“Gs-Ge”表示数据异常段，估计弹道偏差表示真实弹道与估计弹道的坐标差值，测量弹道偏差表示真实弹道与测量弹道的坐标差值。

图3(a)～图3(c)中在3个坐标方向上，测量弹道偏差和EKF估计弹道偏差在“Ls-Le”段存在明显的波峰，表明3个方向上的测量数据出现了偏差，而且一般EKF算法并不能有效地降低测量误差，其估计误差与测量弹道偏差的变化基本一致，但是在正常接收数据的阶段，EKF算法仍然可以在一定程度上降低测量数据误差。3条曲线中，改进的UKF估计弹道偏差变化平稳，且比测量弹道偏差和EKF估计弹道偏差要小。另外，“Gs-Ge”段只在x轴方向和y轴方向出现，说明出现了定位失锁或者有粗大误差数据，经过滤波处理，EKF估计弹道偏差在“Ls-Le”段和“Gs-Ge”段仍然出现了很大的偏差，与测量误差几乎一致，在数据正常接收阶段，EKF算法亦可以降低测量误差；而纵观整个时间轴，3个方向上的UKF估计偏差不仅变化平稳，而且小于测量弹道偏差和EKF估计弹道偏差。图3(d)中，从“Ls-Le”段明显看出，观测弹道在此阶段没有接收到动态数据，如果没有数据处理的过程，而弹道解算的初始数据恰好选择在这一段，则将无法解算出正确的修正时刻；然而观察图3中改进UKF算法的估计弹道可知，在“Ls-Le”段和“Gs-Ge”段仍然可以正常预测出弹道数据，由此解决了信号丢失的情况，而且在GPS重新定位后弹道并没有大的偏差，说明信号丢失时算法预测的弹道数据具有一定的可信度，而EKF估计弹道与真实弹道之间的偏差仍然较大。

3.2 改进射程修正算法

根据一维弹道修正的基本原理，将3.1节图2所示基于改进UKF的弹道数据处理算法融合于修正算法中，则基于UKF的修正控制算法解算步骤如下：

步骤1初始化P(0)、X(0)以及数据接收起始时刻ts0.

步骤2确定t0时刻的状态向量X(0)=(x(t0),y(t0),z(t0),v(t0),θa(t0),ψ2(t0))T，假设ωx、ωz为0；将其作为弹道解算的初始条件，通过修正算法确定粗略估计修正时刻tc0，在时间段ts0～tc0之间进行弹道数据的滤波处理。

步骤3通过改进UKF算法处理接收的N组弹道数据，满足N<(ts0-tc0)fGPS+1，fGPS为接收机频率。

步骤4由步骤3可得到状态量在N+1时刻的最佳估计值，将其作为弹道修正算法新的解算初始条件来求解最优的修正时刻值tc.

由图2可知，在UKF算法中预测sigma点集时，对于非线性状态方程进行了离散化采样处理，因此需要对离散化步长进行选取。第4节仿真分析将确定GPS数据处理算法中离散化步长h以及最佳预处理的弹道数据样本数N.

4 仿真与试验分析

4.1 仿真分析

以新40管火箭弹为仿真研究对象，为了模拟实际得到的具有误差的弹道数据，设弹道数据产生的初始条件X(0)=(0 m, 0 m, 0 m, 130 m/s, π/4 rad, 0 rad)，ωx=0 m/s，ωz=0 m/s，弹丸自身基本参数设置参照前文。在给定的初始条件下仿真计算得到无控弹道的射程为957.8 m，在以下算例中，设定目标射程为800 m，则粗略估计的修正时刻为7.58 s，产生理想弹道数据的步长分别为0.10 s、0.15 s、0.20 s，则N的最大值分别为76、53、41. 对于离散化步长的取值问题，由于篇幅所限，在此直接给出仿真分析的结论：当离散化步长h取值与GPS数据更新周期相等时，UKF算法处理弹道数据后再进行落点预测，其射程均值偏差和Ex都有明显降低。因此，为了最大化UKF算法处理弹道数据的优势，建议将h取值为GPS数据更新周期。

为进一步验证上述结论，仿真计算设置射角为25°，离散化步长h的取值与GPS数据更新的周期相等，分别等于0.10 s、0.15 s以及0.20 s，弹道数据处理前后预测的落点射程均值偏差和Ex的变化如图4所示。从图4(a)中可以明显看出，离散化步长h的取值与GPS数据更新的周期相等时，采用改进UKF算法处理弹道数据后再进行落点射程预测，其偏差远远小于直接利用含有误差的弹道数据进行预测的射程偏差，而且Ex也远小于后者。

4.1.1 预处理数据组数N的选择

根据分析，h=1/fGPS时可以最大化改进UKF算法的优势，因此在讨论N(处理的数据组数)的取值时，以GPS更新频率为10 Hz情况讨论，h取值0.10 s作为算例的已知条件。根据N<(ts0-tc0)fGPS+1的条件可知N<76，本文选择N为5～50来研究N取值对预测的落点精度和Ex的影响，并以每5组为增量变化N值。仿真结果如图5所示。图5(a)为采用改进UKF算法处理弹道数据后再预测弹道落点的射程均值和采用未经处理的弹道数据预测弹道落点射程均值，以及理想弹道落点射程均值的对比；图5(b)为对应不同预测方法得到的Ex对比变化图。

由图5可知：1)UKF算法处理弹道数据后再进行弹道落点预测可降低射程均值偏差和Ex；2)当N≤10时，有如图6所示的结果，UKF算法处理后得到的射程均值偏差和Ex波动较大，且Ex相对于N>10时大，但仍然满足结论1，出现这种情况的原因在于算法收敛速率的限制；3)在一定范围内N的变化对UKF算法效果的影响不是非常明显。图5(a)和图5(b)中改进UKF算法处理的变化均较平缓，表明N的取值在超过某个阈值后，对于落点精度的影响不是很大，故N的选择在实际运用中将更加灵活。

4.1.2 基于改进UKF修正算法的修正精度分析

根据基于UKF修正算法的原理可知，最优弹道数据估计状态量(N+1)将作为弹道解算的初始条件来解算修正时刻c，而原算法只能利用观测到的弹道数据作为解算初始条件。为了验证改进后的算法确实可以降低测量数据的误差，假设仿真次数为100次，即m=100，进行Monte Carlo仿真分析，对比第2节表1中分析的GPS定位误差对修正精度的影响，图7所示结果是通过改进UKF算法处理弹载数据后，预测的修正射程均值偏差和Ex与数据处理前的对比。由图7可以看出，在目标射程变化时，修正射程均值偏差和Ex的变化都比原算法更加平稳，且有明显的降低。

4.2 试验分析

根据仿真分析的结论，在实际试验中采用3.2节所提基于UKF的修正算法对弹载测量数据进行处理，分别进行无控飞行和修正弹道试验。弹丸发射流程如下：首先通过智能火控系统给弹上GPS系统及弹载计算机装定星历、环境信息及目标信息，装定成功后断开连接器，启动弹上电源，4～5 s后弹载GPS系统完成定位，可随时根据智能火控系统指令发射弹丸。设定修正射程为850 m，弹载GPS接收机数据接收频率为10 Hz，根据从弹载存储系统中读回的数据做出如图8、图9所示的弹道轨迹图，其中对于无控飞行测量数据，UKF算法对全部数据进行处理，另外图9中根据最优估计弹道数据预测了理想修正弹道轨迹。图10为修正试验弹落地状态。由于新40管火箭弹在出炮口后有一段助推加速阶段，此阶段扰动较大，GPS开始接受数据起始点在加速阶段完成后的某一时刻。由无控飞行弹道轨迹的对比可知，改进的UKF处理弹道数据确实在一定程度上降低了测量数据误差。而由UKF处理后的最优估计弹道参数预测的修正弹道落点可以很准确地定位到目标处。修正弹丸落点与发射点实测距离约860 m，从测量弹道轨迹的变化趋势和最后靶场落点距离来看，弹丸较准确地落在预定目标距离范围内。当然，由于未考虑横风等其他扰动因素影响，这一试验结果与仿真结果存在一定误差，但可以证明本文的改进算法应用在射程修正算法上可以减小GPS测量误差造成的影响。

5 结论

基于GPS的弹道射程修正弹基本修正原理，本文在预处理GPS测量数据过程中，采用UKF算法，对定位丢失情况和异常测量数据进行了判别和修正，将改进后的UKF算法应用到修正控制算法中。通过仿真分析，确定了最优滤波参数。实际射击试验表明，改进后的算法应用在射程修正算法中，可以减小GPS测量误差造成的影响，对该类弹药工程设计有一定的帮助。