基于不完全信息随机博弈的防御决策方法

2018-09-25杨峻楠张红旗张传富

网络与信息安全学报 2018年8期

杨峻楠，张红旗，张传富

基于不完全信息随机博弈的防御决策方法

杨峻楠1,2，张红旗1,2，张传富1,2

（1. 信息工程大学，河南郑州 450001；2. 河南省信息安全重点实验室，河南郑州 450001）

现有防御决策中的随机博弈模型大多由矩阵博弈与马尔可夫决策组成，矩阵博弈中假定防御者已知攻击者收益，与实际不符。将攻击者收益的不确定性转换成对攻击者类型的不确定性，构建了由静态贝叶斯博弈与马尔可夫决策结合的不完全信息随机博弈模型，给出了不完全信息随机博弈模型的均衡求解方法，使用稳定贝叶斯纳什均衡指导防御者的策略选取。最后通过一个具体实例验证了模型的可行性和有效性。

网络攻防；随机博弈；不完全信息；贝叶斯纳什均衡；防御决策

1 引言

随着信息化程度的不断加强，网络给人们提供了更多便利，但是网络攻击也日趋频繁，给受攻击者造成巨大损失[1]。政府、企业和学校等机构每年都要在网络安全上投入大量资金，但是由于网络本身的复杂性以及当前技术的限制，导致无法保证网络绝对的安全，亟需一种技术能够对攻防行为进行分析，对网络风险与安全投入进行有效折中，使防御者能够利用有限的资源做出合理的决策。博弈论与网络攻防所具有的目标对立性、关系非合作性和策略依存性高度契合[2]。基于博弈论的网络安全研究逐渐成为一个热点[3]。

目前，国内外基于博弈论的网络攻防行为分析与防御策略选已取得较多成果。很多学者使用单阶段博弈对网络攻防进行分析。文献[4]基于静态博弈理论对蠕虫病毒攻防行为进行分析，采用贝叶斯纳什均衡对防御策略进行指导。文献[5]基于动态博弈理论研究DDoS的攻防行为并依据精练纳什均衡设计了最优防御策略选取算法。单阶段博弈能够在一定程度上指导网络防御，但其只能分析一个攻防回合，而攻防对抗往往由多阶段组成，为了能够更加符合实际，部分学者开始使用多阶段博弈对网络攻防进行建模分析。文献[6]构建多阶段攻防信号博弈模型研究最优主动防御策略选取问题，并给出了博弈均衡求解方法。文献[7]针对无线传感器网络中的安全防御问题，构建了多阶段重复博弈模型。上述成果虽然可以对攻防对抗的多个回合进行分析，但是只考虑了攻防双方对网络对抗的影响，忽略了网络本身对攻防进程的影响。网络状态的转移不仅受到攻防动作的影响，还受其他一些因素的影响，其状态转移呈现随机性。上述成果没有对这种随机性进行分析，削弱了其指导价值。随机博弈[8]是一种多阶段博弈，其采用马尔可夫过程描述博弈系统的状态转移，能够准确刻画网络攻防对抗过程。文献[9]将攻击者的特权状态作为网络状态构建完全信息随机博弈模型，对攻防的收益量化进行分析并依据纳什均衡提出了防御策略选取算法。文献[10]使用随机博弈对网络对抗问题进行研究，运用凸分析理论证明均衡的存在性并将均衡求解转换为一个非线性规划问题。Wei等[11]利用完全信息随机博弈分析攻击者与防御者之间的策略交互，利用纳什均衡评估不同状态下系统面临的风险。Ding等[12]在完全信息随机博弈的框架下，研究了传感器与DoS攻击者之间的相互作用过程，根据纳什均衡给出了传感器的最优功率方案。上述研究的随机博弈由矩阵博弈与马尔可夫决策组成，使用马尔可夫决策描述网络的演进，使用矩阵博弈分析各回合攻防双方的决策。由于攻防双方的目标对立性，完全掌握对手信息几乎不可能，而上述成果中使用的矩阵博弈以完全信息假设为前提，与实际不符。

基于上述分析，为解决网络防御决策问题，将防御者对攻击者收益的不确定转换成对攻击者类型的不确定，构建由静态贝叶斯博弈与马尔可夫决策结合的不完全信息随机博弈模型，针对博弈模型给出了一种非线规划求解方法，依据稳定贝叶斯纳什均衡对攻击行为进行预测和对防御策略进行指导。

本文的主要贡献如下。

1) 从攻防策略的角度将复杂的网络攻防问题抽象为一个双人、非零和的不完全信息随机博弈问题。

2) 借鉴现有的完全信息随机博弈求解方法，给出了本文不完全信息随机博弈模型求解方法。

3) 使用本文方法对一个典型的网络攻防场景进行了分析，提供了一个详细的实例。

2 不完全信息随机博弈及防御策略选取

2.1 问题描述与分析

网络攻防对抗是一个复杂问题，本文主要从决策角度对其进行研究。网络攻防对抗包含3个主要对象，分别是攻击者、防御者和网络本身。攻防双方依据自己的策略选择攻防动作，网络在攻防双方的联合行为作用下进行演进。由于网络中一些未知因素的影响，导致攻防演进呈现不确定性。网络对抗中攻防双方都是理性的，双方的目的是获得最大收益，这是双方制定攻防策略的准则。

本文的研究对象是企业、政府和学校等局域网，网络管理员作为防御者负责全网的防御措施，攻击者来自外网，远程对局域网发起攻击。在攻防过程中，攻防角色不会互换，即防御者仅采取防御动作，不会以攻代防。

2.2 不完全信息随机博弈模型

使用随机博弈对网络攻防过程进行建模分析。网络攻防是一个连续过程，对其进行离散化处理，将整个时间轴划分为一个个时间片，每个时间片有且只有一个网络状态，攻防双方在每个网络状态依据攻防策略选择攻防动作，网络在攻防双方的联合行为作用下由一个状态转移到另一个状态。网络状态独立于时间，即不同的时间片内，可能有相同的状态。攻防策略与网络状态相关联，而与时间片无关。使用随机博弈对网络攻防建模主要分为2个部分。

1) 建立每个网络状态的博弈模型

在实际中，同一时刻可能有不止一个攻击者攻击网络，但是对于防御者来说，这些攻击者是无差别的，防御者可以将不同攻击者当作是一个集体，将不同攻击者的行为看作是同一个攻击者的不同行为，这样，网络攻防对抗就可以使用一个双人博弈进行分析。

攻击者的收益受攻击目标、攻击者能力等多方面因素的影响，又由于攻防双方是非合作关系，导致最终防御者往往无法确定攻击收益函数，即攻击收益对防御者是未知信息，所以网络攻防是一个不完全信息博弈。本文使用海萨尼转换[13]对其进行处理，将防御者对攻击者收益的不确定性转化为对攻击者类型的不确定性，攻击者类型为攻击者的私有信息，但是防御者对攻击者类型分布有一个概率判断，这个概率判断为共同知识。攻防双方的收益受多种因素影响，两者之间并不是简单的零和，故非零和博弈更符合攻防对抗实际。

由于攻防双方的非合作性，攻防双方只能通过检测网络了解对手行动，这往往比动作的执行时间有所延迟，所以在每个状态，攻防双方可以认为是同时行动，这里的“同时”是一个信息概念而非时间概念，即双方在决策时可能不在同一时刻，但只要双方在决策时不知道对方在当前状态的选择，就认为双方是“同时”行动。

上述分析将每个状态的攻防对抗抽象为一个双人、非零和不完全信息静态博弈。

2) 建立网络状态之间的转移模型

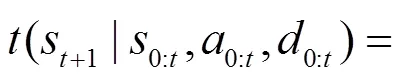
至此，已将网络攻防抽象为一个双人、非零和的不完全信息随机博弈，随机博弈由贝叶斯静态博弈与马尔可夫决策组成。在此基础上构建不完全信息随机博弈模型（II-SGM, incomplete information stochastic game model）。

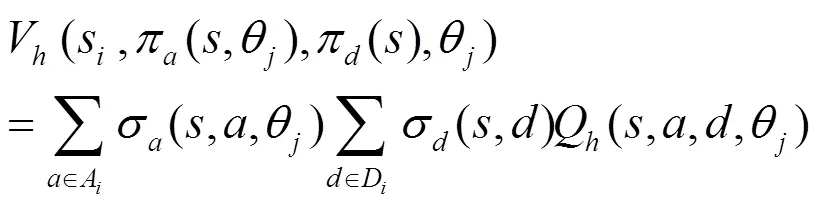
利用海萨尼公理，通过引入虚拟参与人“自然”，将防御者对攻击收益的不完全信息转换为对“自然”行动的不完美信息，这样就可以使用标准技术对其进行博弈分析。在这些基础上构建一个时间片的博弈树，如图1所示。博弈由上一个时间片转移到当前时间片后，“自然”按照转移概率先选择当前时间片的网络状态，再按防御者对攻击者类型分布的概率判断选择攻击者的类型，攻击者A和防御者D都能观察对状态的选择，但只有攻击者能观察到对攻击者类型的选择。A和D观察后依据策略选择自己的动作，当前时间片的博弈结束，博弈转移到下一个时间片。

2.3 稳定贝叶斯纳什均衡策略分析及求解

网络攻防对抗具有策略依存性，攻防双方的最优策略依据对手策略的变化而变化，双方在制定策略时，会对对手的策略进行预测，根据预测结果选择自己的最优策略，也会预测到对手对自己的预测，从而进一步调整自己的策略，双方的预测和调整是一个螺旋上升过程，而贝叶斯纳什均衡就是这个螺旋上升过程的最终状态。根据贝叶斯纳什均衡定义可知，均衡策略是攻防双方根据对手策略做出的最优响应，任何一方无法通过单方面努力提高自己的收益。综上可知，利用贝叶斯纳什均衡进行攻击预测和防御策略选取是一种合理、有效的方法。

Shapley[15]提出了一种值迭代方法求解由矩阵博弈与马尔可夫决策结合的随机博弈，但是该方法计算复杂度高，求解效率低。Filar[16]等将由矩阵博弈和马尔可夫决策结合的随机博弈的求解问题转化为一个非线性规划问题，该方法是目前求解随机博弈的主流方法。本文在Filar等的基础上给出由静态贝叶斯博弈与马尔可夫决策结合的随机博弈的求解方法。

图1 攻防博弈树

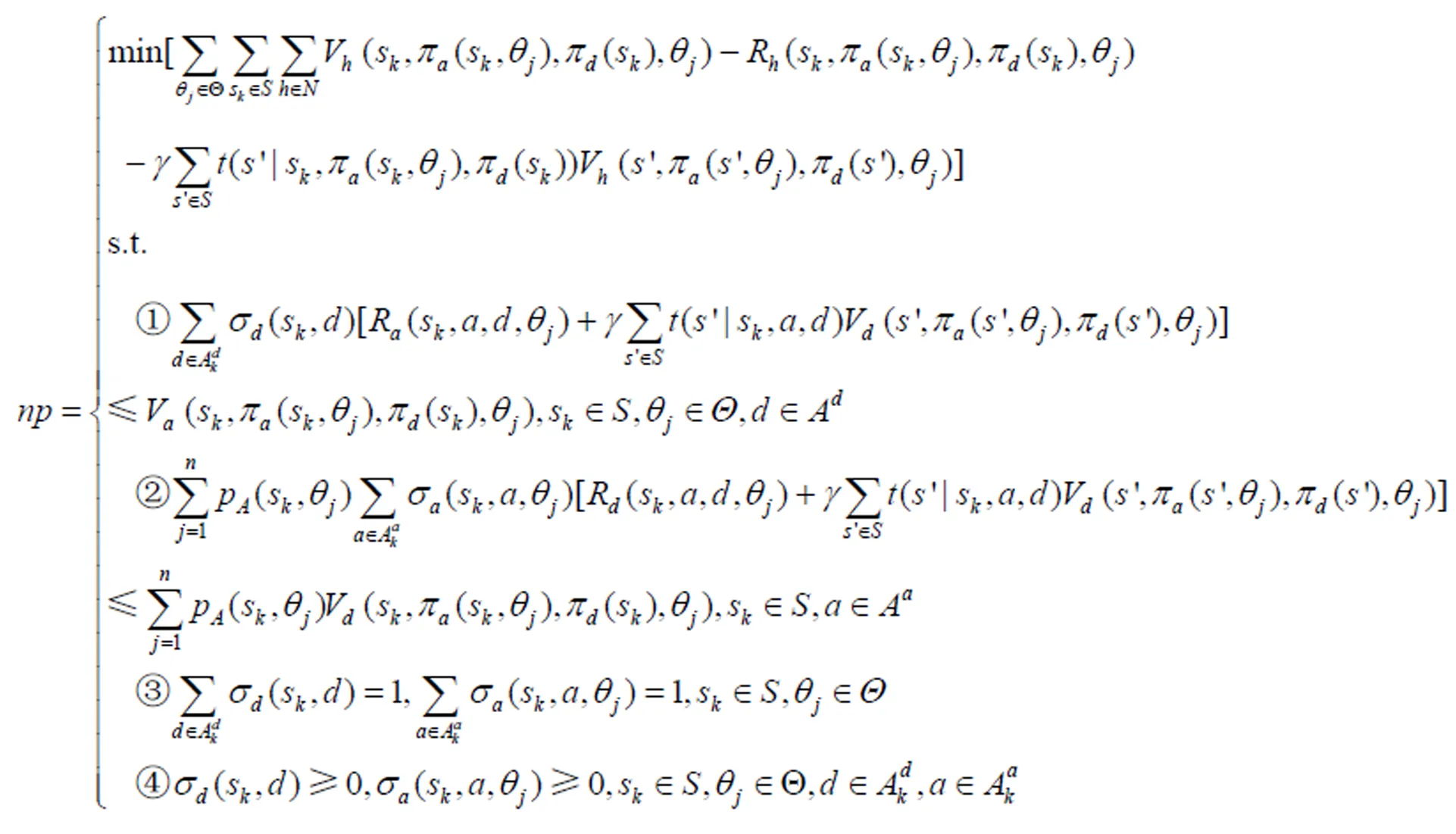
证明

1) 必要性

2) 充分性

证毕。

3 实例分析

3.1 攻防场景

使用本文方法对一个典型企业网络进行分析，其拓扑结构如图2所示。攻击者来自外网，远程对内网发起攻击。防御者为内网管理员，负责全网的网络安全防御。防火墙的策略为外网正常用户只能与内网的Web服务器和内网用户通信，且只能访问Web服务器的HTTP和FTP服务，其他网络节点和端口均进行阻断。参考NVD数据库[17]给出企业网络脆弱性信息，如表1所示。参考美国麻省理工大学的攻防行为数据库[18]给出防御动作，如表2所示。

3.2 场景建模

图2 实验网络拓扑结构

表1 实验网络脆弱性信息

表2 实验网络防御动作

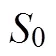
防御者对攻击者类型的概率判断为

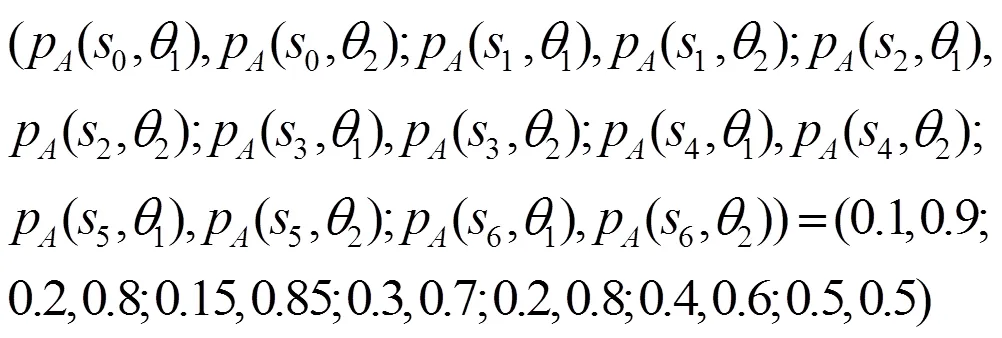
表3 转移概率

表4 立即回报

表5 立即回报

3.3 稳定贝叶斯均衡求解

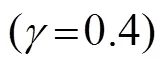
3.4 结果分析

由上文的分析可知，稳定贝叶斯纳什均衡中的攻击策略是对攻击行为的可信预测。根据不同攻击类型的均衡策略及攻击者类型分布概率可以计算出每个状态下脆弱性被利用的概率。

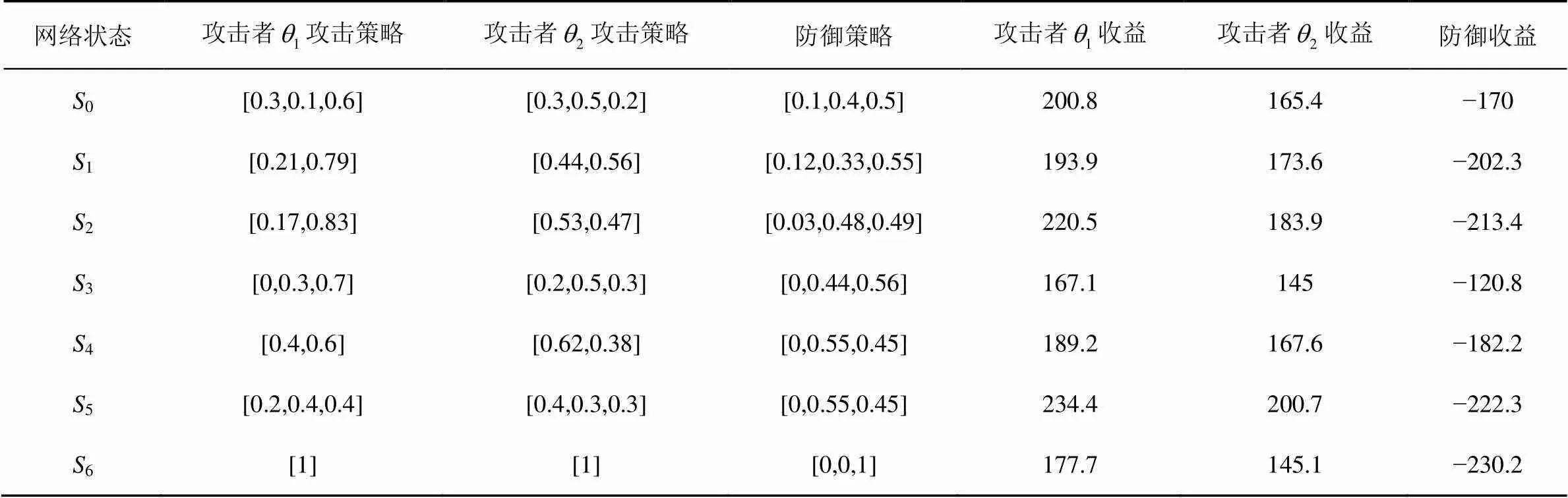
表6 网络攻防博弈均衡及收益值

4 结束语

基于博弈论的网络安全研究是现在网络安全领域的主要发展方向之一。为解决网络防御决策问题，本文将复杂的网络攻防对抗描述为一个随机博弈问题。针对网络安全领域现有随机博弈模型以完全信息假设为前提，与实际不符的问题，本文将防御者对攻击者收益的不确定性转化为对攻击者类型的不确定性，建立由静态贝叶斯博弈与马尔可夫决策结合的不完全信息随机博弈模型对网络攻防进行分析，通过稳定贝叶斯纳什均衡进行攻击预测和防御策略选取。借鉴现有由矩阵博弈与马尔可夫决策组成的随机博弈的求解方法，给出了本文不完全信息随机博弈模型的非线性规划求解方案。最后通过一个典型的企业网络攻防场景，给出了本文方法的一个详细应用实例。

现有网络状态转移概率往往是由专家知识或历史经验确定，准确性较差。下一步拟将强化学习引入随机博弈中，使防御者通过在线学习修正网络状态转移概率的误差，以获得更高的防御收益。

[1] LIANG X, XIAO Y. Game theory for network security[J]. IEEE Communications Surveys & Tutorials, 2013, 15(1):472-486.

[2] WANG Y Z, YU J Y, WEN Q, et al. evolutionary game model and analysis methods for network group behavior[J]. Chinese Journal of Computers, 2015.

[3] FALLAH M S. A puzzle-based defense strategy against flooding attacks using game theory[J]. IEEE Transactions on Dependable & Secure Computing, 2010, 7(1):5-19.

[4] 刘玉岭, 冯登国, 吴丽辉,等. 基于静态贝叶斯博弈的蠕虫攻防策略绩效评估[J]. 软件学报, 2012, 23(3):712-723. LIU Y L, FENF D G, WU L H, et al. Performance evaluation of worm attack and defense strategies based on static Bayesian game[J]. Journal of Software, 2012, 23(3):712-723.

[5] GAO X, ZHU Y F. DDoS defense mechanism analysis based on signaling game model[C]// International Conference on Intelligent Human-Machine Systems and Cybernetics. IEEE, 2013:414-417.

[6] 张恒巍, 李涛. 基于多阶段攻防信号博弈的最优主动防御[J]. 电子学报, 2017, 45(2):431-439. ZHANG H W, LI T. Optimal active defense based on multi-stage attack-defense signaling game[J]. Acta Electronica Sinica, 2017, 45(2): 431-439.

[7] SHEN S, LI Y, XU H, et al. Signaling game based strategy of intrusion detection in wireless sensor networks.[J]. Computers & Mathematics with Applications, 2011, 62(6):2404-2416.

[8] ALLAMIGEON X, GAUBERT S, SKOMRA M. Solving generic nonarchimedean semidefinite programs using stochastic game algorithms[C]// The ACM. ACM, 2016:31-38.

[9] 姜伟, 方滨兴, 田志宏, 等. 基于攻防随机博弈模型的防御策略选取研究[J]. 计算机研究与发展, 2010, 47(10):1714-1723. JIANG W, FANG B X, TIAN Z H, et al. Research on defense strategies selection based on attack-defense stochastic game model[J]. Journal of Computer Research and Development, 2010, 47(10): 1714-1723.

[10] 王长春, 程晓航, 朱永文,等. 计算机网络对抗行动策略的Markov博弈模型[J]. 系统工程理论与实践, 2014, 34(9): 2402-2410. WANG C C, CHENG X H, ZHU Y W, et al. A Markov game model of computer network operation[J]. Systems Engineering - Theory & Practice, 2014, 34(9):2402-2410.

[11] WEI L, SARWAT A I, SAAD W. Risk assessment of coordinated cyber-physical attacks against power grids: A stochastic game approach[C]//Industry Applications Society Meeting. IEEE, 2016:1-7

[12] DING K, DEY S, QUEVEDO D E, et al. Stochastic game in remote estimation under DoS attacks[J]. IEEE Control Systems Letters, 2017, 1(1):146-151.

[13] HARSANYI J C. Games with Incomplete Information Played by “Bayesian” Players, I–III Part I. The Basic Model[M]. Springer Netherlands, 1982:159-182.

[14] LEI C, ZHANG H Q, WAN L M, et al. Incomplete information Markov game theoretic approach to strategy generation for moving target defense[J]. Computer Communications, 2018, 116:184-199.

[15] SHAPLEY L S. Stochastic Games[J]. Proceedings of the National Academy of Sciences of the United States of America, 1953, 39(10):1095-1100.

[16] FILAR J, VRIEZE K. Competitive Markov decision processes[J]. Springer Berlin, 1996, 36(4):343-358.

[17] ZHANG S, OU X, CARAGEA D. Predicting cyber risks through national vulnerability database[J]. Information Systems Security, 2015, 24(4-6):194-206.

[18] GORDON L, LOEB M, LUCYSHYN W, et al. 2015 CSI/FBI computer crime and security survey[C]. Proceedings of the 2014 Computer Security Institute//San Francisco: IEEE, 2015. 48-64.

Defense decision-making method based on incomplete information stochastic game

YANG Junnan1,2, ZHANG Hongqi1,2, ZHANG Chuanfu1,2

1. Information Engineering University, Zhengzhou 450004, China 2. Henan Province Key Laboratory of Information Security, Zhengzhou, 450001,China

Most of the stochastic game models to select network defense strategies are composed of matrix game and Markov decision, which assumes that the defender has known the attacker's revenue. This assumption does not conform to the actual situation. The uncertainty of the attacker's income was converted into the indeterminacy of the attacker type, and an incomplete information stochastic game model, which was combined with the static Bias game and Markov decision, was constructed. The equilibrium solution method of the incomplete information stochastic game model was given, and the strategy selection of the defender was guided by the stable Bias Nash equilibrium. Finally, a practical example was given to demonstrate the feasibility and effectiveness of the model.

network attack-defense, stochastic game, incomplete information, bayesian nash equilibrium, defense strategies

TP393.08

10.11959/j.issn.2096-109x.2018065

杨峻楠（1993-），男，河北藁城人，信息工程大学硕士生，主要研究方向为网络信息安全、博弈论和强化学习。