外部电场对三角束缚势量子点量子比特概率密度的影响

尹辑文

1 引言

近年来，各领域的科学研究者们将量子理论应用于物质科学和能源科学，开拓出诸如半导体、激光、核技术等重要高新技术.本世纪，一门新兴的交叉学科——量子信息科学应运而生，它是量子力学与信息科学相互融合的结果.在过去几年里，对不同物理系统用做量子信息载体，人们进行了诸多的理论和实验研究[1-8].由于各种物理系统应用于量子计算机各有利弊，人们目前正在寻找影响量子计算机性能的各种因素.本论文以Li等人[9-10]提出的参数相图方案为前提，研究讨论了外部电场对三角束缚势量子点量子比特的概率密度的影响.

2 理论模型

设在单一电子量子点中,电子在z方向比x和y方向受限强得多，设电子在x-y平面内运动，仅考虑电子-体纵光学声子耦合，电子的束缚势为三角束缚势可写为

其中m*为电子的有效质量,ρ为二维坐标矢量,ω0为量子点的受限强度,沿x方向加电场F，则在电场作用下电子-声子体系的哈密顿量为

其中bq+(bq)为波矢为q(q=q∥,q⊥)的体纵光学声子的产生(湮灭)算符,r=(ρ,z)为电子坐标矢量,e*是电子电荷

为了计算方便，采用极化子单位(ħ=ωLO=2m*=1)，系统的哈密顿量可以写为

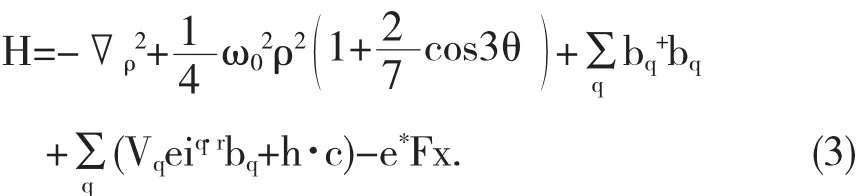
其中

α为电子-LO声子的耦合强度.

对哈密顿量(3)作LLP变换

其中fq是变分函数，则

在高斯函数近似下，依据Pekar类型的变分法，电子-LO声子系统的基态尝试波函数可以选为

电子-LO声子系统的激发态尝试波函数可以选为

其中，λ0和λ1为变分参量，|0ph〉为无微扰零声子态，bq|0ph〉=0，|0〉、|1〉满足

由 E0=〈ø0|H"|ø0〉，E1=〈ø1|H"|ø1〉通过分法可以得到变分参量λ0和λ1，进而可得到基态和激发态能量及其本征波函数，得出了一个量子比特所需要的二能级体系，当电子处于这样一个叠加态

叠加态随时间的演化可以表示为：

3 结果和讨论

为了更直观的看出电场对三角型量子点量子比特的影响，数值结果表于如下图中.

图1（a-e）电子在空间的概率密度分布随时间的演化

图2 概率密度Q随电场强度F和电子-声子耦合强度α的变化关系

图2 给出的是受限长度θ=0.2、极角为θ=0.2时，概率密度Q(ρ，θ，t)随电场强度F和电子-声子耦合强度α的变化关系.从图2可以看出，概率密度 Q(ρ，θ，t)随着耦合强度增大而增大.同时从图中可以看出概率密度Q(ρ，θ，t)随着电场的增加而减小.并且电子-声子耦合强度越大，电场强度F对概率密度 Q(ρ，θ，t)的影响越明显.由于电场的存在约束了基态和第一激发态的能量，同时电场对激发态能量的影响比对基态能量的影响要明显，导致了能量差随电场强度的增大而减小.

4 结论

本论文应用Pekar类型的变分方法，研究了电子与光学声子的耦合强度、极角和电场对量子点量子比特概率密度的影响.研究发现，当极角取确定的值θ时，电子的概率密度将以一定周期在空间振荡，是极角的周期性函数；概率密度随电场强度的增大而减小，随耦合强度的增大而增大.综上，可以看出外部电场和电子与光学声子的耦合强度对量子点量子比特的微观性质有明显的影响.