简化积分计算的一类方法
2018-09-23陈丹丹
陈丹丹
在《高等数学》的学习中,很多人会被一些积分难题困扰.本文就探讨了一类简化积分计算的方法,利用积分区域的对称性和被积函数的奇偶性简化积分计算.
1 利用积分区间对称性和被积函数奇偶性简化定积分计算
根据定积分的定义和性质,可以利用牛顿—莱布尼兹公式:如果F(x)是连续函数f(x)在区间[a,b]上的任意一个原函数,则有f(x)dx=F(b)-F(a).
换元积分法和分部积分法也是求定积分的基本方法.我们在研究定积分的计算方法的过程中,发现利用积分的对称性和被积函数的奇偶性是简化定积分计算的一个重要方法,对此我们有如下定理:
定理1 设f(x)在[-a,a]上连续,若f(x)为偶函数,则
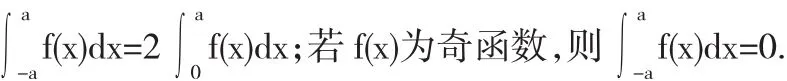
2 利用积分区域对称性和被积函数奇偶性简化二重积分计算
二重积分的计算方法是根据计算体积的原理,将它化为累次积分来计算的,因此,定积分中利用积分区域的对称性和被积函数的奇偶性计算积分的方法,也可推广到二重积分上.
定理2 设f(x,y)在有界闭区域D上可积,

同理也可以推出D关于y轴和关于x轴y轴对称结论.
由该方法可以减少累次积分的计算量,使一些看上去复杂的积分问题简单化,为利用对称性,有时需将被积函数分拆分,将积分区域分成若干个对称子区域.
例 2 设 D 是平面上以 A(1,1),B(-1,1)和 C(-1,-1)为顶点的三角形,D1是它的第一象限部分,则

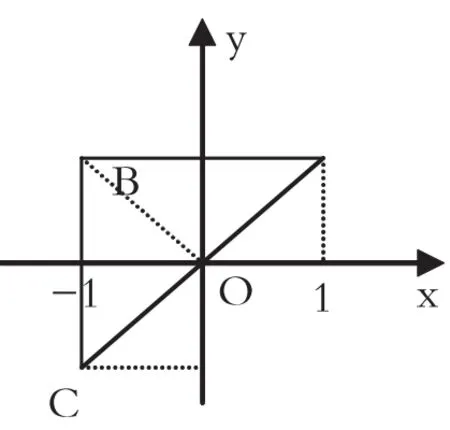
解 如图所示:连接BO,把 D 分成 D'1∪D2,D'1即三角形 AOB,D2即三角形COB.由于D'1关于y轴对称,被积函数xy关于x为奇函数;关于x轴对称,xy关于y为奇函数.
而D'1关于y轴对称,被积函数cosxsiny关于x轴为偶函数,D2关于x轴对cosxsiny关于y为奇函数.所以

3 利用积分区域对称性和被积函数奇偶性简化三重积分计算
三重积分相对复杂,也可以利用积分区域的对称性和被积函数的奇偶性来简化积分计算,并且该方法也是计算三重积分的一个重要方法,其规律如下:
定理3 设f(x,y,z)在Ω上连续,若Ω关于平面xoy对称,则当函数f(x,y,z)是z的奇函数,即f(x,y,-z)=-f(x,y,z)时,有;当函数f(x,y,z)是z的偶函数,即f(x,y,-z)=f(x,y,z)时,有f(x,y,z)dv;其中Ω1是Ω内z≥0的部分.同理可以得出Ω关于平面xoz对称和关于平面yoz对称的结论.
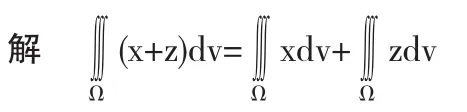
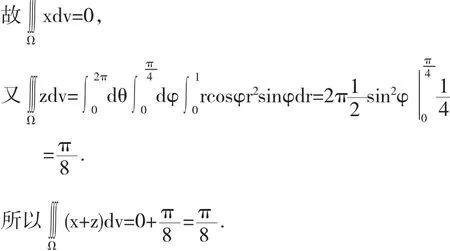
三重积分的计算,一般来说都需要计算多步,有的被积函数甚至比较繁,但如果能用上“对称性”,则可能会收到意想不到的效果,但在利用“对称性”的同时,也不能忽略被积函数的奇偶性.
4 利用积分区域对称性和被积函数奇偶性简化曲线积分计算
曲线积分和曲面积分是多元函数积分学的另一重要内容.同样可以利用区域对称性和被积函数的奇偶性来简化它们的计算.
定理4 设f(x,y)是定义在光滑或分段光滑的曲线L上
的连续函数.若曲线L关于x轴对称,则 ∫Lf(x,y)ds=2∫L1f(x,y)ds,当f(x,y)关于y是偶函数,L∫f(x,y)ds=0,当f(x,y)关于y是奇函数,其中L1是L在y≥0的那段曲线,即L1是L在上半平面的部分.
同理可以得出L关于y轴对称和关于原点对称的结论.
解 由于xy关于x(或y)为奇函数,且椭圆L关于y轴(x轴)是对称的,所以L∮xydx=0,只需计算L∮(3x2+4y2)ds.又由于椭圆L可表示为3x2+4y2=12,所以有L∮(2xy+3x2+4y2)ds=(3x2+4y2)ds=12L∮ds=12a.
可见,利用对称性和被积函数的奇偶性也可简化第一类曲线积分的计算.类似于第一类曲线积分,第二类曲线积分也有如下一些性质:
若L∫Pidx+Qidy(i=1,2,…,k)存在,则也存在,且Qidy),其中 ci(i=1,2,…,k)为常数.
若有向曲线L是有向曲线L1,L2,…,Lk,首尾相接而成,且Pdx+Qdy(i=1,2,…,k)存在,则 ∫LPdx+Qdy也存在,且 ∫LPdx+Qdy=
同样可以利用积分区域的对称性和被积函数的奇偶性简化第二类曲线积分的计算.
定理5 设L为平面上分段光滑的定向曲线,P(x,y),Q(x,y)连续,
(1)若L关于x轴对称,并且L1为L在上半平面的部分,
则
∫LPdx=0,当P关于y为偶函数,∫LPdx=2∫L1Pdx,当 P 关于y为奇函数;
∫LQdy=0,当Q关于y为奇函数,∫LQdy=2∫L1Qdy,当Q关于y为偶函数;
同理可以得出L关于y轴对称和关于原点对称的结论.
(3)若L关于原点对称,则L∫Pdx+Qdy=0,当P,Q关于(x,y)为偶函数,∫LPdx+Qdy=2∫L3Pdx+Qdy,当P,Q关于(x,y)为奇函数.

解法1 将原式分为两部分
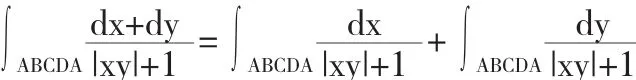
因第一个积分曲线关于x轴对称,且走向相反,被积函数为y的偶函数,第二个积分曲线关于y轴对称,且走向相反,被积函数为x的偶函数,所以两积分值均为0,即

解法2 因曲线ABCDA关于原点对称,又P(x,y)=Q(x,y)关于(x,y)为偶函数,所以原式=0.
5 利用积分区域对称性和被积函数奇偶性简化曲面积分计算
曲面积分分为第一类曲面积分和第二类曲面积分,第一类曲面积分的性质完全类似于第一类曲线积分的性质.第一类曲面积分利用对称性有如下定理.
定理6(1)若分片光滑的曲面∑关于xoy平面对称,且∑1:z=z(x,y)≥0,则

同理可以得出分片光滑的曲面∑关于xoz平面对称和曲面∑关于yoz平面对称的结论.
解 因为∑关于xoy平面对称,且sinxsinysinz是z的奇函数,所以sinxsinysinzds=0.
第二类曲面积分的性质也完全类似于第二类曲线积分的性质,且第二类曲面积分奇偶对称性的说法与第一类曲面积分有所不同,在积分曲面关于某坐标面(例如yoz面)对称的前提下,第一类曲面积分的说法是:被积函数(关于x)为奇函数时积分值为0;而第二类曲面积分的说法是:被积函数(关于x)为偶函数时积分值为0.
定理7 设分块光滑定向曲面∑关于xoy平面对称,f(x,y,z)在∑上连续,则f(x,y,z)dxdy=0,当f关于z为偶函数,f(x,y,z)dxdy=2f(x,y,z)dxdy,当f关于z为奇函数,其中∑1为∑在xoy平面上方部分,其方程为z=z(x,y),(x,y)∈Dxy.
同理可以得出分片光滑的曲面∑关于xoz平面对称和曲面∑关于yoz平面对称的结论.
证明 由第二类曲面积分的可加性,有

其中∑1为∑在xoy平面上方部分,其方程为z=z(x,y),(x,y)∈Dxy,∑1'为∑在xoy平面下方部分,其方程为z=-z(x,y),(x,y)Dxy.
由分块光滑定向曲面∑关于xoy平面对称可知:
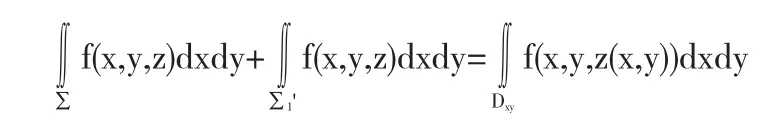

若f(x,y,z)关于z为奇函数,
则


由于x2+y2+x2≤1,关于平面y=0对称,siny为y的奇函数,故
6 结束语
综上所述,利用此方法简化此类积分的计算,但具体使用上有所不同.在二重积分,三重积分的计算中,是利用积分区间的对称性及被积函数的奇偶性来简化计算.在第一类曲面积分中,若积分区间内关于某坐标平面对称,而被积函数是另一变元的奇函数,则其积分值为0.在第二类曲面积分,若积分曲面关于其面积元素两个同名变元的坐标平面对称,而被积函数又是另一变元的偶函数,则其积分值为0.如果能合理有效地运用积分区域的对称性和被积函数的奇偶性来简化此类积分的计算,那么解决许多之前似乎不易解决的问题就会变得又快又准确.
