MATLAB软件在数值分析课程中的应用

牛潇萌

1 引言

数值分析是研究数据结构和数量关系的数学分支，在信息与计算科学、物理学、数学与应用数学等专业的教学中都是一门很重要的专业课.其内容包括插值方法、数值积分、数值微分、常微分方程的差分方法、方程求根的迭代法，线性方程组的迭代法和线性方程组的直接法等.

在许多情况下，要获得精确解是十分困难的，有时是不可能的，例如，由于找不到的原函数，所以用牛顿-莱布尼茨公式就不能求解定积分到因此研究各种数学问题的近似解变得非常重要了，数值分析就是专门研究各种数学问题的近似解的一门课程.因而数值分析是现代计算科学的必要理论基础，作为数学与应用数学专业选修课，数值分析对学习其它专业课是必不可少的.

《数值分析》课程学习的主要困难在运算过程、运算公式复杂，不能简单的靠一支笔就能算出来，而需要通过计算机来执行运算[1-3].本文将以《数值分析》课本中一些容易实现的例子来说明MATLAB在《数值分析》课程教学过程中的重要应用.

2 数值分析实验步骤

数值分析课本中有很多流程图，需要上机实验，在数值分析课程的实验教学中可以让学生按如下步骤做数值分析实验并写出数值分析实验报告：

（1）算法描述；

（2）编写算法实现的M文件；

（3）用具体实例运行M文件，得出运行结果或者图形.

下面以秦九韶算法为例，让学生对数值分析上机实验有所了解.

（1）秦九韶算法的公式[4]

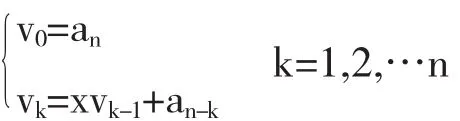
（2）算法流程图

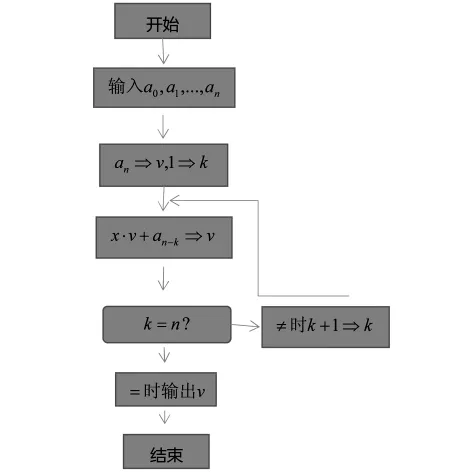
（3）秦九韶算法实现的M文件

根据上述流程图，用MATLAB编写算法的M文件，代码如下：

function v=qinjiushao(x,a)

%其中a是多项式的系数

[hang,lie]=size(a);

n=lie;

v=a(n);

k=1;

while k～=n

v=x*v+a(n-k);

k=k+1;

end

（4）用具体实例运行M文件，得出运行结果

利用编写的M文件计算如下多项式：

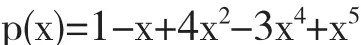
在x=3处的值.

在MATLAB命令窗口输入如下命令

x=3;a=[1-1 4 0-3 1];

qinjiushao(x,a)

得到结果是34.

3 利用MATALB软件将数值分析课程教学直观化

数值分析课程中有许多例子比较抽象，难于理解，教师可以利用MATALB强大的绘图功能，将这些例子直观化，便于学生理解，加深印象.下面以高次插值的龙格现象说明此问题.

在讲解高次插值的龙格现象时，教师可以用MATLAB编写程序演示，让学生直观上认识到随着插值节点的增加，高次插值多项式的逼近效果有时是不理想的.考虑如下函数

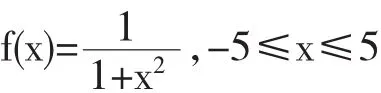
首先编写如下M文件:

function f=myrunge(i)

x=linspace(-5,5,i);

y=1./(1+x.^2);

p=polyfit(x,y,i-1);

xx=-5:0.01:5;

yy=polyval(p,xx);

plot(xx,yy);

其次在区间[-5,5]内取6个节点和11个节点来画图，验证龙格现象.

hold on

myrunge(6)

gtext('p_5(x)')

myrunge(11)

gtext('p_{10}(x)')

xx=-5:0.01:5;

plot(xx,1./(1+xx.^2),'r')

gtext('f(x)')

title('龙格现象')

得到如下图像.

4 结论

本文通过数值分析课本上的几个例子，给出了MATLAB软件在数值分析教学过程中的应用.数值分析教学过程中使用MATALB软件可以解决教学过程中很多题目无法手算的难题.这也有助于培养学生的编程能力，将数值分析应用到实际问题中的能力.