汉明窗在屏蔽效能计算中的应用

王 志，汪 青

1 引言

在信号处理中，可以说加窗处理是一个必经的过程，汉明窗就是信号窗口的一种.我们为了充分利用FDTD方法与优势，已经对腔体的结构进行模拟与仿真，从根本上克服腔体谐振对FDTD方法迭代时间步的增加，本文引入汉明窗技术，对电场信号进行滤波，从而使得电场信号无需衰减到很小（时间步数急剧增加）也可以得到更准确的SE结果，这可以减少仿真时间，并提高FDTD方法的计算效率.

2 汉明窗技术

离散时间信号在实践中总是受到限制的，因此，不可避免地要遇到数据截断的问题.在信号处理中，通过将序列与窗函数相乘来实现离散序列的截断.汉明窗具体公式如下：

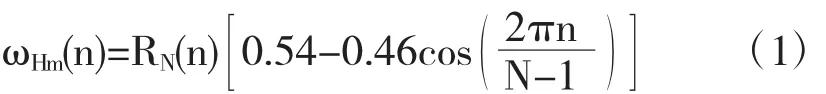
其频谱函 WHm(ejω)

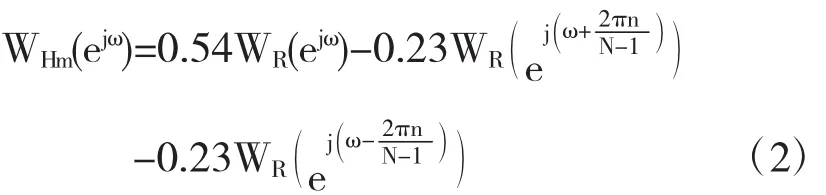
其幅度函数WHmg(ω)

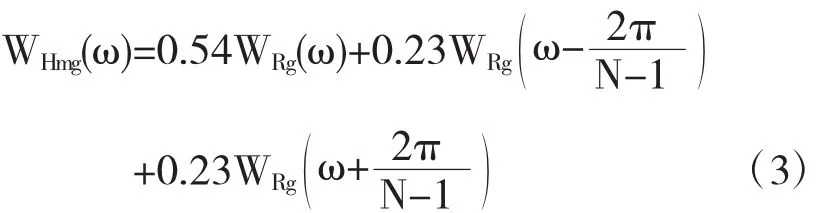
当N≥1时，其可近似表示为

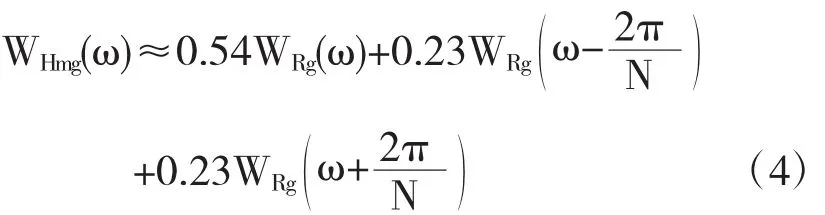
3 汉明窗在屏蔽效能中的应用

3.1 汉明窗技术精度验证

我们数值验证的第一种几何结构，金属外壳上仅有一个水平的缝隙，没有加载细线天线.计算区域用立方网格来进行离散化.其中Δx=Δy=Δz=1cm，时间步长为Δt=Δx/(2c0).为了节约仿真时间，在所有仿真过程中数据从时域到频域的转换过程中都用到汉明窗.缝隙的宽度是0.5cm.图1是Modal/MoM法计算出来的SE和文献中的测量结果.比较这两个结果可以看到本论文提出来改进FDTD算法比模匹配/矩量法（Modal/MoM）算法要更精确些.在最低SE水平对应的频率f≈707MHZ.在该频率处TM110模式在矩形金属屏蔽体中被激发出来.

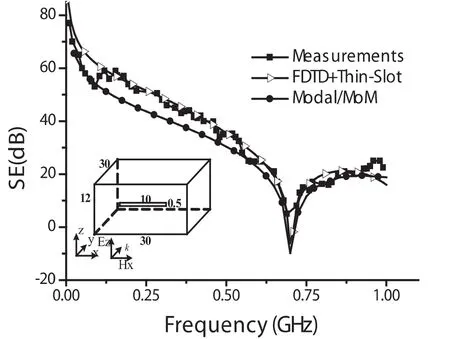
图1 SE结果比较

可以明确的发现FDTD算法比矩量法要吻合实际测量值，所以说FDTD算法要更精确些.

3.2 典型机箱结构屏蔽效能计算

对于高功率脉冲，我们主要采用表面开孔的方式来提高通信系统的屏蔽效能.本文中，我们主要分析表面采用周期性的细缝和矩形开槽情况下，机箱或机柜的屏蔽效能和内场分布情况，具体的设计结构以及尺寸如图2和3所示.结构1的几何参数是 ：d=13mm,L1=L3=356mm，L2=150mm，L4=38mm，L5=74mm，L6=38mm，L7=46mm，L8=85mm，L9=3mm，L10=85mm，L11=85mm，L12=49mm.结构 2的几何参数是 ：d=13mm,L1=L3=356mm，L2=150mm，L4=23mm，L5=25mm，L6=25mm，L7=34mm，L8=23mm，L9=50mm，L10=20mm，L11=70mm，L12=70mm，L13=34mm.

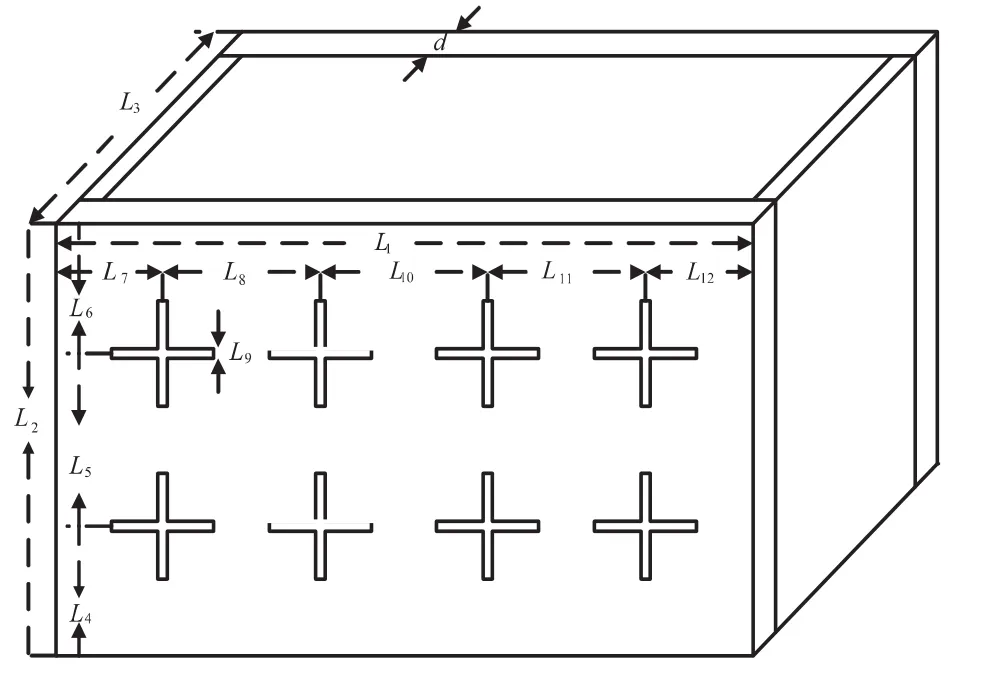
图2 箱体表面采用周期形的细缝选择表面(结构1)

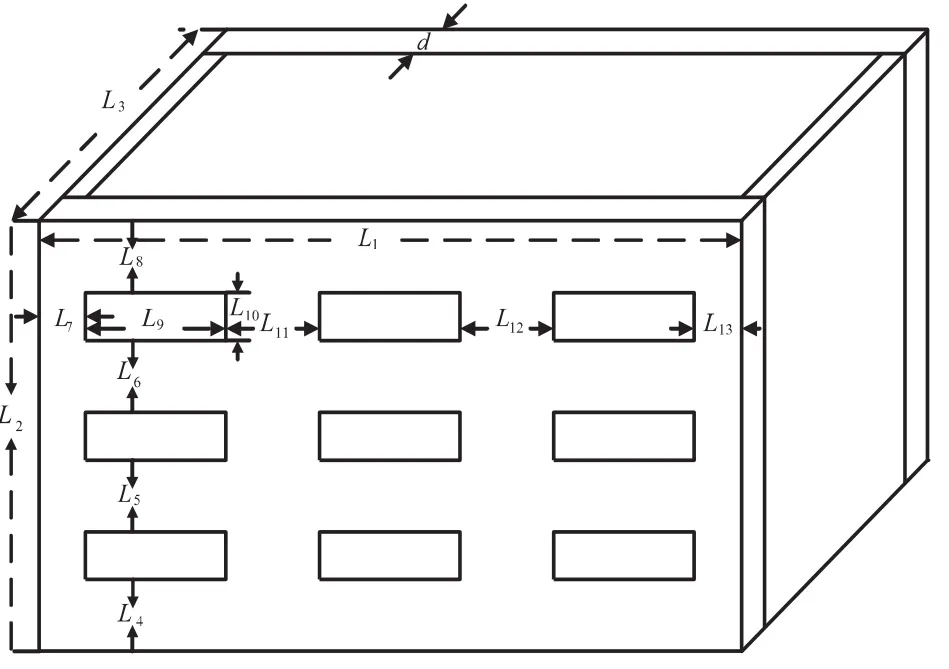
图3 箱体表面采用周期形的矩形选择表面(结构2)

图4 和5给出了机箱中心的电场分量随时间变化的曲线，可以看出采用两种不同结构时电场的三个分量依然随时间振荡十分严重，但是和原来的结构在同样的条件下的耦合电磁场相比，采用结构1时电场的分量下降了一个数量级以上，采用结构2时电场幅度为原来的三分之一左右.图6给出了结构1、2和原结构屏蔽效能的比较，采用结构1时箱体屏蔽效能提高20分贝以上，采用结构2时箱体屏蔽效能提高了8分贝以上.

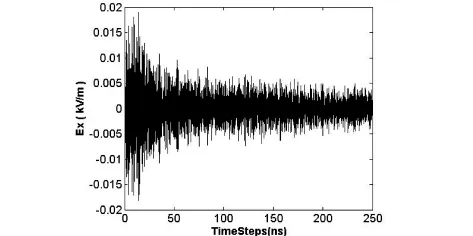
图4 表面采用周期形的细缝结构的内场分布

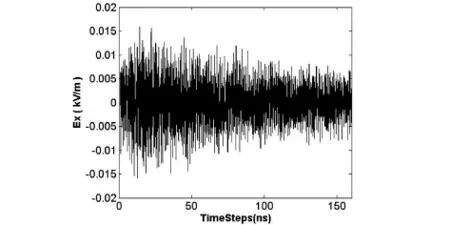
图5 表面采用周期形的矩形结构的内场分布

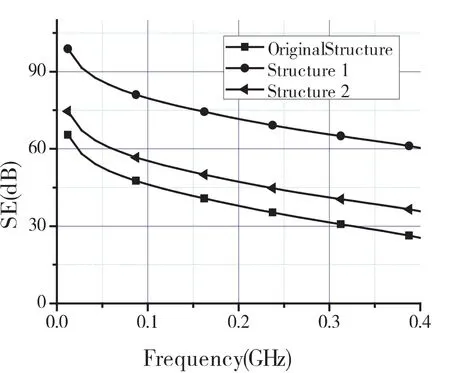
图6 屏蔽效能对比

4 结论

文中通过对屏蔽腔体的电磁脉冲耦合效应研究，利用屏蔽效能(SE)参数对其屏蔽特性进行了评析.我们主要考察了开细缝和矩形孔缝情况下矩形屏蔽腔体对应的屏蔽效能，重点研究了将汉明窗技术引入屏蔽效能FDTD方法仿真中，可大大降低FDTD方法的迭代时间，提高仿真效率.

通过研究发现，腔体开缝结构和取向会影响屏蔽效能.这与腔体表面的电流分布密切相关，并且发现细缝结构要比矩形结构的屏蔽效能好很多，在同样开缝面积的情况下，矩形口要优于圆形口.