基于BP神经网络的城市物流需求预测模型研究

林伟滨

引言：在物流行业不断发展壮大的背景下，各省市也逐渐制定出符合自身发展的物流战略，并且将其纳入到城市规划当中，期望能够通过物流业的发展带动整个城市的经济发展.但是，过快的增长很容易导致物流供求间的不平衡，因此城市规划者需要对物流需求进行准确的预测，采用BP神经网络的方式，模仿大脑神经结构建立新型的信息处理系统，以此来提升预测的有效性与准确性.

1 BP神经网络结构概述

1.1 概念

BP神经网络处于目前应用范围较广的人工神经网络，它具有前向多层性，将一层或者多层单元隐含在输入和输出层中间，如图1所示，该图属于一个三层BP网络，并且其中包含一个隐含层，与相邻两个层之间相互连接，但是每个层的内部神经元之间又处于相互独立的状态.

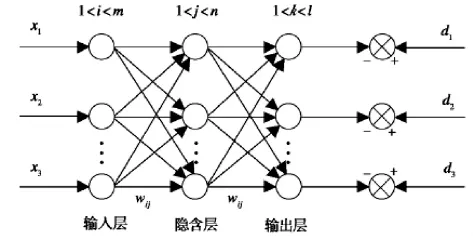
图1 三层BP网络结构图

对于BP网络来说，其主要采用误差反向传播的算法，主要理念在于，设置好输入与期望输出后进行网络训练，采用前向逐层计算的方式，计算出网络中实际输出与期望值之间的误差，从而对权限进行判断，直到结果与期望值相符合后才结束，否则偏差则会按照原本的网络以反方向进行传播，也就是由输出层朝着相反的方向逐渐对联接权重进行调整，最终使误差与规定范围相符合.在输入层当中，神经元个数的计算由输入信号维数来决定，而隐含层与节点的个数由客观实际所决定，因此输出层中神经元的数量与信号维数之间几乎相同.

1.2 学习过程

以上图1为例，对三层BP网络学习算法的学习过程进行分析.

（1）初始化，将全部权重都设置到最小的数值，然后得出初始阈值；

（2）设置特定的训练数据，输入向量为X，其取值范围为x1，x2，……xm，期望输出向量为 D，其取值范围为 d1,d2,d3……dm；

（3）由输入层开始，采用前向传播的方式开始逐层计算；在对输入层神经元的计算中，xi代表输入向量，oi代表输出向量，oi的取值范围与xi相同，i的取值区间均为1,2，3……m，i代表的书输入层维数.对于输出层神经元的计算中，输入向量为ω'ijo'i-θ'j，输出向量为 yk=g(x"k)，其中，k的取值范围为1,2,3……l，k代表的是输出层维数.对于隐含层层神经元的计算中，输入向量为x'jωijxi-θj，输出向量为oj=f(xj)，其中，j的取值范围为1,2,3……n，j代表着的是隐含层的维数[1].

综上，ωij代表的是由输入到隐含层中的权重；ω'jk代表的是隐含到输出层之间的权重；函数f（·）与g（·）为非线性函数，同时也是可以为线性激励函数.

（4）按照误差反向传播的方式，由输出层开始在各个层次之间往返进行权重方面的调整，在定义网络中的误差为：

根据梯度算法中的规则，对上述函数的权重进行调整后可得：

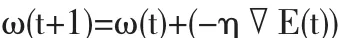
在该式中，▽E（t）代表的是在t次训练的过程中，函数按照梯度变化的相反方向.

对于从输出到隐含层中权重的调整，公式为：

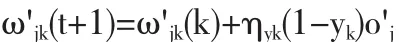
式中，η代表的是学习率，数值范围大于0；dk代表的是期望值，k的取值范围为1,2,3……l.

从隐含到输入层中的权重调整，公式为：

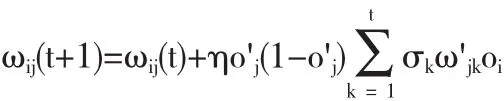
式中，σk代表的是输出层当中k的误差；

（5）如若误差的数值不符合预期范围，则需要对其重新计算，直至误差与期望相符合才能结束[2].

2 城市物流需求度量指标与影响因素

2.1 需求度量指标

通过对现有文献的分析可知，物流需求度量可分为实物量与价值量两种.对于实物量来说，在物流需求方面主要为不同环节中实际作业量，包括仓储量、货运量等等；而价值量物流需求则主要是指物流环节中所有服务价值的整体反应.对于城市物流来说，主要目的是为了满足城市居民生活与经济发展的需求，所研究的主要对象大多为城市内部的物流工作，涉及的范围较广、时间较长，在对价值量的研究方面具有较大难度，国家目前此方面的数据也较少.

2.2 影响因素

城市经济发展促进了社会物流需求，物流需求又反作用于城市经济发展，因此物流量与经济因素之间存在较强的变化关系，由此可见，从理论上来看，根据二者之间的关系构建物流需求模型具有较强的可行性，公式为：

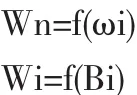
式中，W代表的是物流的需求量；B代表的是城市经济发展的因素；通常对城市物流需求的影响因素较为复杂，涉及面积也较为广泛，本文从货运量方面展开研究，将影响因素归结为以下几个部分，分别为第一产业、第二产业、第三产业、区域零售总额、外贸总额、居民消费水平.

3 城市物流需求预测模型的构建

3.1 数据收集与整理

本文选取的是某市2013-2017年的城市货运数据，将其作为本次研究的网络训练样本，由于数据之间存在不一样的量纲，需要对其进行归一化的处理之后才能使用，保障处理后的数据区间均在0到1的范围内，数据统一化处理的公式为：

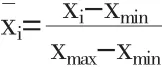
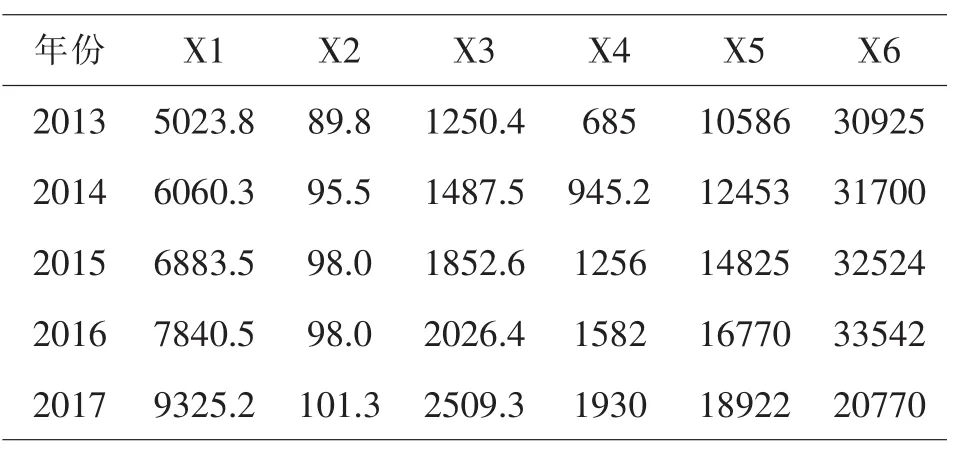
表1 某市货运量与经济指标

本文的研究主要采用Matlab的方式，实现数据的统一化处理.

在表1中，X1代表的是该地生产总值；X2代表的是第一产业产值；X3代表的是第二产业产值，单位为亿元；X4代表的是区域外贸总额，单位为亿美元；X5代表的是居民消费水平，单位为亿元；X6代表的是货运量，单位为万吨.

3.2 BP网络结构设计

3.2.1 输入、输出、隐含节点数

根据上述对影响因素的分析，对生产总值、外贸总额、居民消费水平等因素进行明确以后，将其作为输入节点，将货运总量作为输出节点.对于单隐层的BP神经网络来说，需要通过实验的方式对中间层的神经元数量进行计算.由上表可知，深入神经元有5个，按照Kolmogorov定理可知，首先将网络隐含层中的神经元数量设置为15个，然后分别对10与20进行对比，最终明确最佳神经元个数.通过数据误差的对比分析后可知，当隐含层在红神经元的数量为15时，预测的误差最小，因此处于最佳状态[3].

3.2.2 权值、阈值的确定

在神经网络模型构建之时，需要对网络中的权值、阈值等初始值进行明确，这对于神经网络的学习效果将产生直接影响.因此，可以通过多次预测取平均的方式获取最为稳定的数值.在计算的过程中，通过超过1000次的计算方式使预测的准确性得到有效提升.而城市物流需求的预测则是为了构建城市经济与物流之间的内在关系，并且为物流规划提供有力的参考依据.

3.2.3 传递函数与训练算法

通过相关实验结果能够看出，隐含层中的神经元采用S型正切函数的方式实现神经元的传递，而在输出层当中采用S型对数函数的方式进行传递，获得最佳传递效果.由于正切函数在收敛过程中的速度较快，因此在训练中产生的误差数值较小，本文选择LM法进行训练，次数为1000次，目标为0.0001，学习率为0.1，其他数据根据MATLAB工具箱内容进行处理.在神经元激励函数确定方面，由于网络非线性具有较强的逼近能力，因此通过S型激励函数进行展现，函数形式如下：

其中，a的数值为1.72；b的数值为2/3.

3.2.4 实验结果

在训练的过程中，次数为11次以后，时间大约为0.49s时，网络目标的误差与预期数值相似，均方差为0.000956/0.001.由于在训练时，最初设置的参数不同，导致每次在训练结束后得出的结果也不尽相同，因此可以通过多次训练的方式，使预测的数值与原始数据之间更加接近.

根据训练结果能够得出，BP神经网络模型在准确度方面具有较为明显的优势，预测数据与原始数据之间的差值能够保持在0.1992-2.2395%范围内.由此可见，利用BP神经网络模型对该市的物流需求进行预测和计算具有较大的可行性.

结论：综上所述，在本文的研究中对BP神经网络进行了分析，阐述了整个神经网络模型的学习过程，并且挖掘出了城市物流量预测影响的因素，主要为区域零售总额、外贸总额、居民消费水平等，将其作为神经网络模型的输入层.最后，以某市为例构建BP神经网络进行实证研究，以此来说明BP神经模型在物流量预测中的有效性与准确性.