基于改进神经网络模型的股指预测实证研究

程 浩，孙 妮

0 引言

神经网络具有极强的非线性逼近能力，自学习自适应能力以及泛化能力的优点，在股指短期预测中得到了充分的应用，取得了一些成果，但神经网络学习训练前网络权值通常未做优化，导致网络收敛速度慢并且容易陷入局部最小值.

针对BP神经网络自身的缺陷，本文利用遗传算法较强的全局搜索能力初始化网络权值和阈值，对BP神经网络权值调整过程进行改进，逐层循环对权值进行调整，根据网络输出总误差变化对学习率进行动态调整，并运用改进的神经网络模型对上证指数预测进行实证研究.

1 遗传算法优化的BP神经网络预测模型

1.1 BP神经网络模型

BP神经网络是以反向传播算法为学习算法的多层前馈式神经网络，通常具有3层或3层以上的网络结构，其拓扑结构可分为：输入层、隐含层和输出层.各层神经元通过相应的网络权值即两个神经元之间的连接强度来连接，而同一层的神经元间无连接.BP神经网络学习过程主要采用最速下降法对网络权值进行反复调整，最终使误差函数取得极小值.

以四层结构的BP神经网络为例.令输入层、第一隐含层、第二隐含层以及输出层节点数量分别为I、M、N、O，相应的某个节点分别用 i、m、n、o表示，W、U、V分别表示输入层到第一隐含层的权重系数矩阵，两隐含层连接权重系数矩阵以及第二隐含层到输出层的权重系数矩阵，层间连接权重分别用Wim、Umn、Vno表示.用 θm、Фn、ψo分别表示后三层网络阈值，Sm、Tn、Co分别表示两隐含层以及输出层相应节点的输入，用Do表示第o个输出节点的预计输出.假设训练数据集为X=[X1,X2,…,Xk,…,Xp]，第k个样本对应的实际输出为Yk=[Ok1,Ok1,…,Ok1]，期望输出为Dk=[Dk1,Dk1,…,Dk1].

对所有样本的输入输出值进行计算，得到了所有样本的网络输出总误差，BP算法根据网络输出误差对所有的网络权值进行调整，完成一次网络循环过程，重复操作，多次调整所有的权值，使网络达到目标输出误差从而完成训练.

权值调整过程中，误差信号由后往前传递，逐层修改网络权值，第二隐含层到输出层权值修正为ΔVno(n+1)=(1-mc)ΔV'no(n)+mcΔVno(n)，梯度下降对权值的修正量为[1-Oko(n)][Dko(n)-Oko(n)]Nkn.其中mc表示动量因子，η1表示第二个隐含层与输出层的学习率，n是网络迭代次数，△Vno(n)表示上次权值调整量，△V'no(n)表示本次梯度下降法对权值的调整量.

通过上述的BP神经网络学习算法，就可实现样本数据的学习训练.可以看出，各层的连接权值和阈值的选取对于BP神经网络的训练非常重要，在使用中经常出现设置不合理导致网络的收敛速度慢并且不易得到最优解的现象，如何优化初始权阈值是BP神经网络研究的重点问题.

1.2 遗传算法优化的改进BP神经网络模型

针对BP神经网络容易陷入局部最小值以及网络收敛速率缓慢等问题，利用遗传算法较强的全局搜索能力初始化网络权值，对BP神经网络权值调整过程进行改进，使每层连接权值采用同一个学习率，逐层循环对权值进行调整，根据网络输出总误差额变化对学习率进行动态调整，加快网络收敛速率并有效减少网络震荡次数.

1.2.1 动态学习率的调整策略

采用差异学习率调整策略，使学习率分层进行调整，调整方向为从后向前，每层调整时采用不同的学习率，并且使每层网络权值优化到一定程度之后再继续调整上一层权值.为了加快网络收敛速度，在调整过程中采用动态学习率调整，使每层的学习率根据网络输出总误差的变化动态改变.改进算法将经典算法单循环过程分为一个大循环多个小循环过程，大循环依照小循环的网络输出总误差增减情况不断改变学习率的值，大循环的权值不受小循环权值改变量的影响.

1.2.2 遗传算法优化的网络权值调整

利用遗传算法全局搜索能力较强的特性对BP神经网络所有权值和阈值进行初始化与初步优化，当网络输出总误差下降到一定程度之后，再将最优的染色体带入BP网络中进一步优化，直到网络输出总误差达到预期值.具体算法的实现过程如下：

（1）染色体编码设计.采用实数编码的方式，将BP神经网络所有权值和阈值按一定顺序排列组成一个染色体.用rowW表示要输入层到第一隐含层权重矩阵W的行展开矩阵，rowU表示第一隐含层到第二隐含层权重矩阵的行展开矩阵，rowV表示第二隐含层到输出层权重矩阵V的行展开矩阵.当遗传算法迭代到一定程度之后，需要将最优染色体中的权值和阈值赋值给BP网络，由于BP网络按逆序方向调整权值，因此需要计算T的逆序矩阵T=[rowW,rowU,rowV]，将逆序矩阵的权值和阈值代入BP网络继续优化，直到达到预期网络输出总误差.

（2）适应度函数设计.遗传算法根据适应度函数对染色体进行优良选择，适应度函数和BP网络的网络输出总误差呈反比关系，网络输出总误差越大，染色体的适应能力越小，适应度函数相应较小.本文采用网络输出总误差的倒数加一来表示适应度函数.

（3）选择算子.遗传算法选择算子使用轮盘赌选择方法进行选择操作.遗传算法根据适应度函数值选择个体不断进化的过程对应于BP神经网络不断优化网络权值，使网络输出误差不断减小.

（4）交叉算子.使用多点交叉方式，使适应度值较大的染色体遗传到下一代的概率相对较大.

（5）变异算子.使用多点变异策略，通过改变权值或阈值的数值来获得网络输出总误差更小的权值阈值组合.

（6）遗传算法优化的连接权值和阈值作为初始值，代入模型进行训练和学习，进而完成预测.

2 实证研究

2.1 实验设计

实验数据选取同花顺和通达信软件提供的2014年1月至2015年3月的上证指数数据，实验前需要将数据进行预处理，使各指标数据分别归一化到[0，1]区间，再代入网络进行计算.

根据多次实验结果，BP网络输入层节点数量为6，对应某日开盘价、收盘价、成交量、振幅、10日和60日均线，输出为第二天的收盘价.设定遗传算法种群个数20，染色体权值从前往后依次对应输入层到网络三层权值矩阵行展开数值.遗传算法交叉点和变异点个数均设置为3，最大迭代次数100.BP神经网络所有学习率的初始值均设置为0.01.在修正权值迭代过程中，设定当网络输出误差增大时调整学习率的误差相对增量阈值1.2，学习率变化率0.98；设定当网络输出误差减小时调整学习率的误差相对增量阈值0.8，学习率变化率1.02，动量因子0.4.

实验时分别使用三层结构和四层结构的BP神经网络对股指数据进行预测，通过实验分析隐含层个数对改进BP算法预测性能的影响.

2.2 实验结果分析

（1）遗传算法的BP网络权值优化

选取上证指数2014年1月至2014年12月的日数据作为训练集，2015年1月至3月的日数据作为测试集进行大量重复实验，网络迭代次数设为300次，实验结果如图1所示.

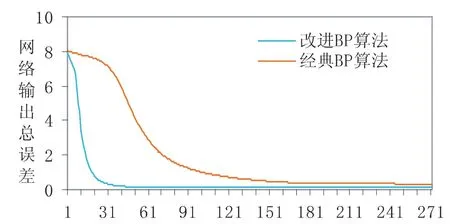
图1 遗传算法对网络收敛性能的影响

用遗传算法对网络权值进行初步优化后网络收敛速度较快，收敛性更好，网络输出总误差较小，网络预测准确度更高.

（2）不同结构实验对比

本文对四层结构网络即双隐含层网络进行了探索，并通过实验对三层结构网络和四层结构网络进行对比，对四层结构网络的收敛性能以及预测准确度进行验证.对比实验结果如图2所示.

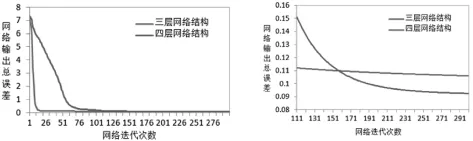
图2 不同结构网络的收敛性能

实验结果表明三层结构网络与四层结构网络预测性能相差不大，三层结构网络的收敛速度相对较快，但当网络迭代超过157次之后四层结构的网络输出总误差小于三层结构网络，，说明四层网络经过多次训练后也能达到较高的预测精度甚至预测准确度较高，适合于对预测精度要求较高的股指预测.

（3）预测结果对比

将本文改进BP算法、经典BP算法运用于上证指数预测，预测结果分别与真实股指数据进行拟合，如图3所示.

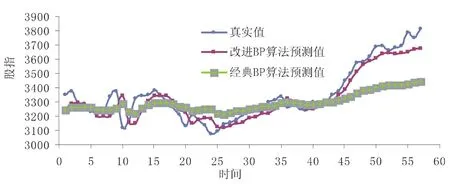
图3 股指数据拟合曲线

相比经典BP算法，改进BP算法预测值与真实值拟合效果更好，预测值与真实值更贴近，随着真实值的波动作出相同方向变动，变动强度比较明显.

3 结论

本文在分析传统BP神经网络局限性的基础上，利用遗传算法对BP神经网络进行优化，根据网络输出总误差变化对学习率进行动态调整，建立基于改进神经网络的股指预测模型，并运用模型对上证指数进行预测分析.预测结果表明：改进BP算法的收敛效率较好，预测精度更高，可以更好地用于股指预测.