广义积分在谐波电流检测中的应用

史 彦

文章对无变压器混合有源滤波器的控制方法进行研究，将广义积分控制技术引入HAPF中，介绍它的控制原理和迭代算法，并通过仿真得到结果，与传统PI控制相比较，得出动态的响应速度和稳态的精度有明显的改善.

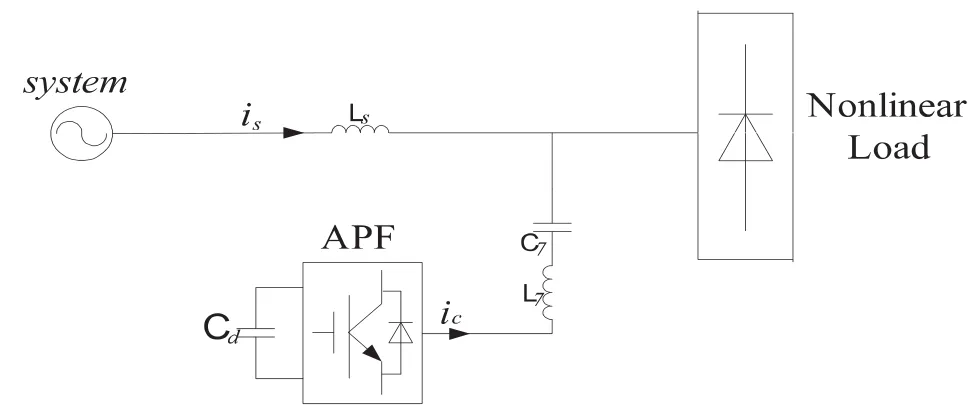
图1 无耦合变压器混合有源滤波器原理图

本研究的无耦合变压器型混合有源电力滤波器原理如图1，设计选取的七次单调谐的电容和电感分别为100μF和2mH，Q取30[1]-[4].

1 检测谐波的方法

有源电力滤波器能否正常工作，谐波检测环节的快速性和准确性起着关键性的作用.

1.1 基于三相瞬时无功理论的ip-iq检测法谐波检测方法

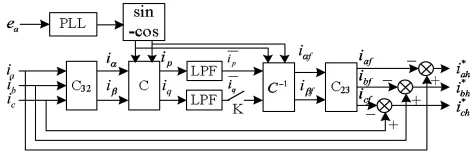
图2 ip-iq检测算法原理框图

从图2中可以得出，基于ip-iq的谐波检测算法[5]不用检测电网电压，它是利用锁相环测出与a相电压相位相同的正弦信号sinωt以及同相位的余弦信号-cosωt.根据公式算出三相瞬时有功电流ip和三相瞬时有功电流iq，再经过低通滤波器处理后得到ip、iq的直流分量ip、iq.通过旋转反变换和2/3 变换，计算出 ia、ib、ic对应的基波分量 iaf、ibf、icf.

再通过公式计算出谐波分量i*ah、i*bh、i*ch.

如果需要同时检测出谐波和无功时，只需将ip断开就可以了，不需检测出ip，当有源电力滤波器只要补偿无功时，把ip断开即可.

1.2 讨论ip-iq算法在三相不平衡负载中的应用

三相不平衡负载电流中含有正序分量、负序分量，但不含有零序分量.可以表达为：

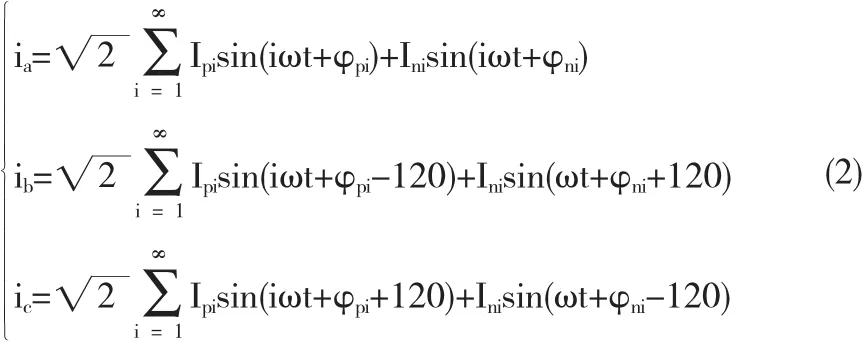
其中：正序用下标p表示，负序用下标q表示；Ipi表示第i次谐波正序分量有效值，Ini表示第i次谐波负序分量有效值；φ表示相位初始角；ω表示电网电压角频率.

将式(2)进行坐标变化到α-β坐标系：

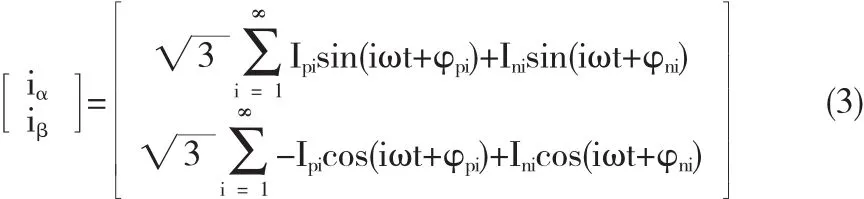
当三相电网电压不对称时，不对称的相电压中包含正序分量、负序分量和零序分量.锁相环所检测出的a相电压相位是三种分量的总和，而我们所期望的得到a相电压相位仅仅含有正序分量，这就导致了期望的相位角与实际检测的相位角有一个相位差θ.则实际的正弦信号和余弦信号分别为 sin(ωt+θ)和 -cos(ωt+θ).

那么实际的ip和iq为：

进而求得ip和iq直流分量：

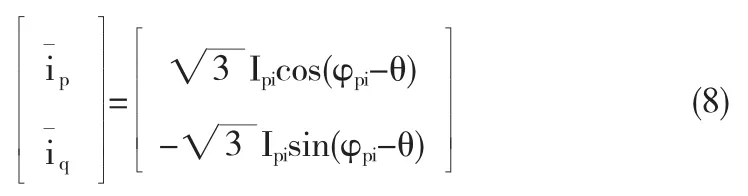
同理进行反变换求得基波正序分量iafp、ibfp、icfp：

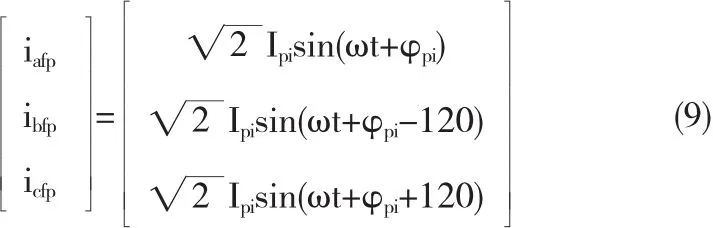
比较式(6)与式(9)，可以看出，当用ip-iq算法检测不对称负载电流谐波和负序分量时，无论三相电网电压是不是对称，结果都不受影响[6-7].

2 谐波电流补偿控制方法的研究

有源滤波器控制系统的一般结构框图可见图3所示.

图3 有源滤波器控制系统的结构框图

2.1 三角波比较控制

图4 三角波比较控制原理

如图4所示，这种控制方法不同于三角波作载波的PWM控制，它不是直接将指令信号i*c与三角载波比较后产生PWM，控制逆变器发波，得到所需的补偿电流.这种控制系统目的是将i*c-ic的值控制为最小，进行闭环控制.

2.2 滞环控制

图5 滞环控制原理

图5 所示的滞环控制方法的原理是将指令信号i*c与实际补偿电流ic比较，将差值作为滞环比较器的输入，通过滞环比较器产生控制逆变器输出的PWM信号，进而跟踪指令i*c的变化.用H表示滞环比较器的环宽，当|ΔIc|＜H时，使滞环比较器的输出保持不变；当|ΔIc|≥H时，使滞环比较器的输出翻转；最终ΔIc是在-H和+H之间不断变化的，而相应的逆变器输出的补偿电流ic会在i*c-H和i*c+H范围内，呈锯齿波形状跟踪i*c.

3 广义积分迭代控制技术

3.1 广义积分基本原理

如果需要输入量在某种控制器作用下，能够保持输出无稳态误差，则控制器中必然包含积分环节.当被控信号是一定频率的周期信号时，如图6所示，经过控制器，信号的频率和相位是不变的，仅对幅值进行积分，这样才能保证无稳态误差输出.

图6 广义积分控制器

通过傅里叶变换可以把任意周期信号分解为不同频率的正弦量相叠加，现以某单一正弦信号为例来介绍广义积分的基本原理.

设某一正弦信号为：

期望经过广义积分器后的信号为：

构造一个辅助信号为：

对上述三个信号进行Laplace变换，可得：

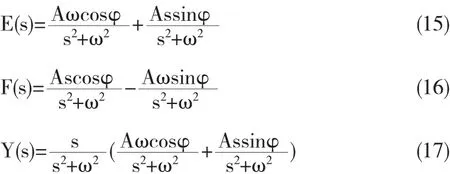
综合式(15)、(16)和(17)可知：

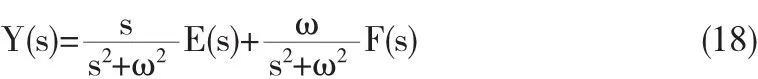
由于：

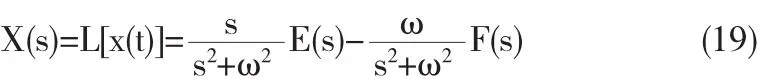
联立式(18)和(19)可得：

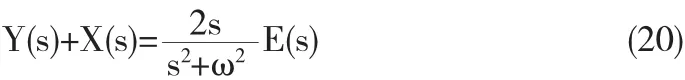
即：

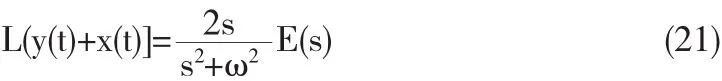
x(t)相对于 y(t)来说可以忽略.故由式（3-40）可知，广义积分的传递函数：

那么，对于频率为ωs的基波的正弦信号的广义积分函数是：

对于频率为ωn的其它谐波的正弦信号的广义积分函数是：

3.2 广义积分迭代算法

运用混合有源滤波器治理谐波时，采样所得的电流信号包含了多次谐波.如果想要得到无稳态误差的跟踪参考信号，这时需将多个频率的广义积分器进行并联.三相全控整流桥的负载是工程中谐波的主要来源，因此只需要考虑比重较大的几种特征次谐波.全控桥主要是6k±1次谐波，补偿其中 5、7、11、13、17次低次谐波后，补偿后的电源电流就十分接近正弦了.所以只要设计与这些特征次谐波相对应的广义积分器，然后再加上比例环节，APF的电流跟踪性能就会特别理想.图7是基于广义积分控制器的控制框图,图中Δish(s)表示指令参考电流ish*(s)和实际电流ish(s)的差值；Kp表示比例系数，Kin表示n次谐波的积分系数.

广义积分的控制输出量如下：

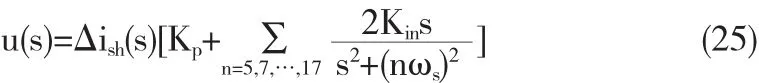
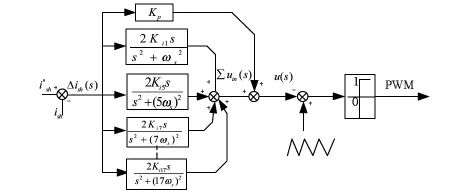
图7 基于广义积分控制器的控制框图

文中运用了一种广义积分迭代算法，此算法通过利用前面的计算结果来求解前量，可以获得方便控制的等效离散量.计算过程大大简化，计算量减少，时间缩短.

4 广义积分在HAPF中的运用研究

前文详细介绍了广义积分的原理和迭代控制算法，现在就其在电压源反馈控制方式下的混合有源滤波器的应用进行仿真.

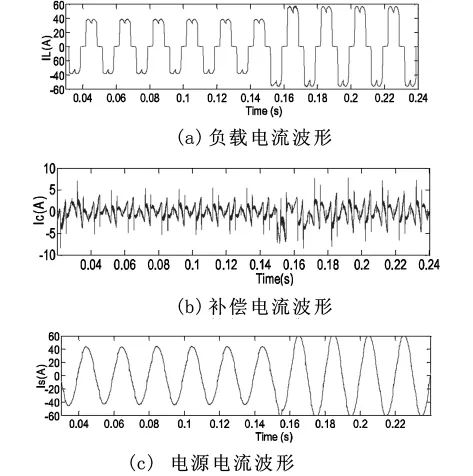
图8 广义积分控制器的系统响应曲线图

图8 是本文算法的电流波形，通过与传统PI比较，发现HAPF能够很好对谐波进行补偿.在0.15s负载发生了突变，运用广义积分控制器控制的有源滤波器具有更快的的动态响应速度，以及更好的补偿效果.

5 总结

文章研究了在混合有源滤波器上加上广义积分算法，通过建立模型仿真，得出引入广义积分的控制器能克服传统PI控制的不足之处，实现控制的无稳态误差，具备很好的滤波效果.