基于随机Taylor展开式的三种随机微分方程半隐式数值求解方法

袁 玲，汪 慧，唐江花，宋 星

1 构造三种随机微分方程半隐式数值求解方法

对于一维自治型Ito随机微分方程[1]：

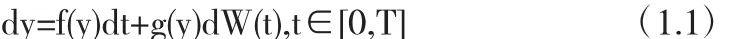
其1.5阶（强收敛阶）半隐式Taylor方法如下：

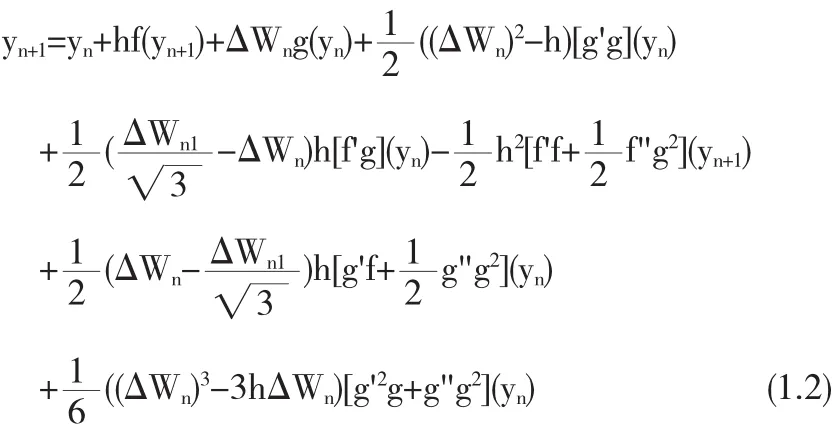
用修正的漂移项[2]f-g'g代替方程中的漂移项f，并用g'(yn)g(yn)(ΔWn)2代替g'(yn)g(yn)h可以得到如下的半隐式Taylor方法：

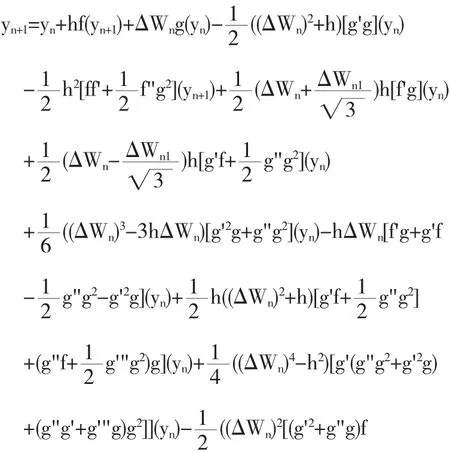
通过截取其中的部分项构造如下三种半隐式方法：

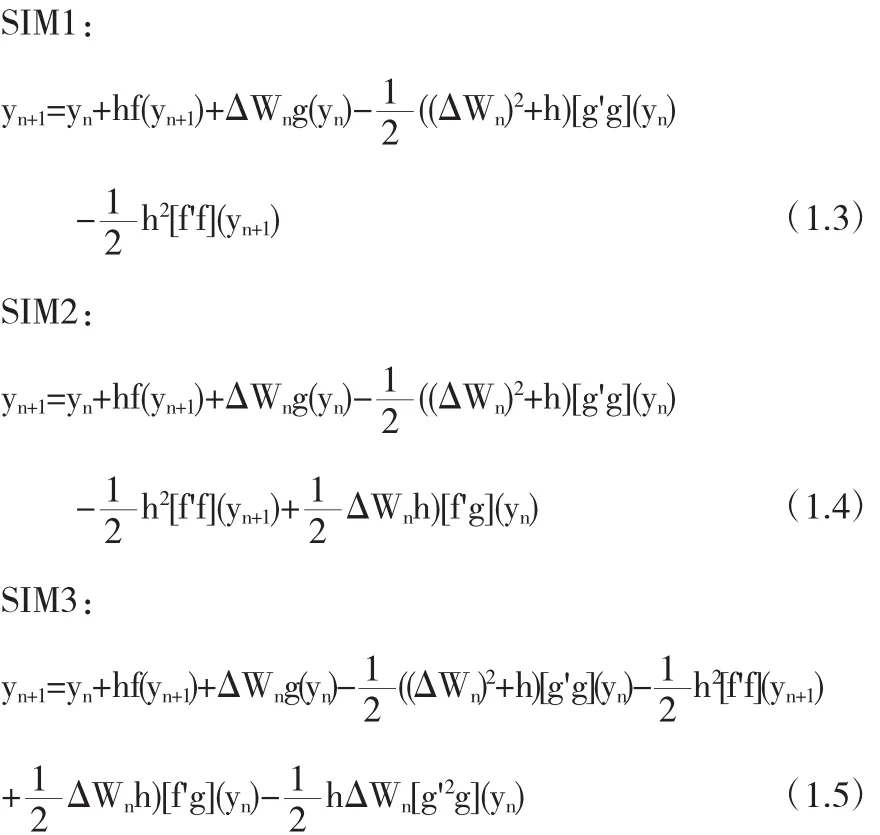
2 均方稳定性分析

选取线性试验方程：

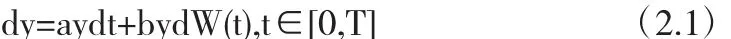
将SIM1方法应用于线性试验方程（2.1）可得：

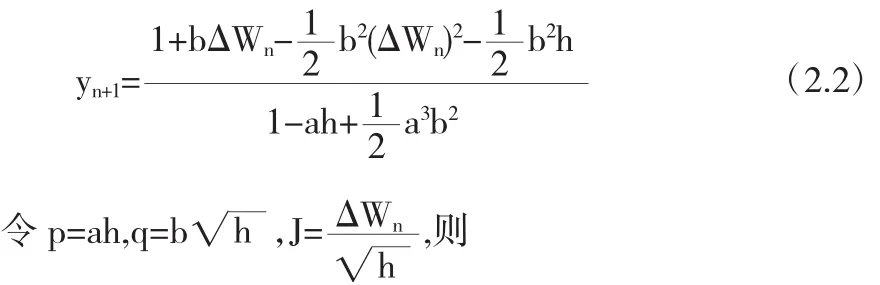
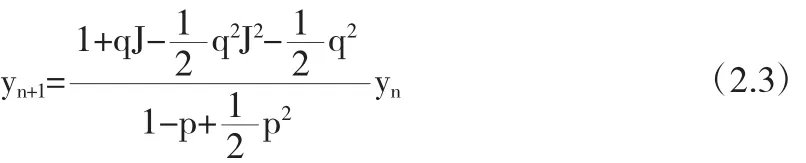
将SIM2方法应用于线性试验方程（2.1）可得：

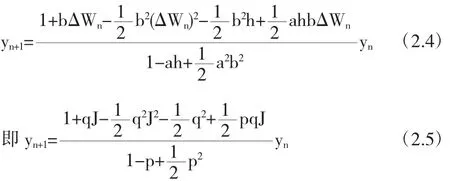
将SIM3方法应用于线性试验方程（2.1）可得：

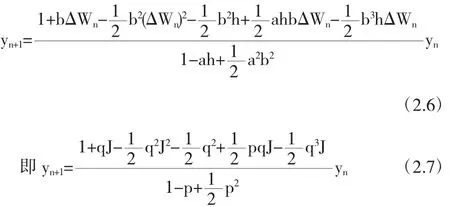
SIM1方法的均方稳定函数[3]为：

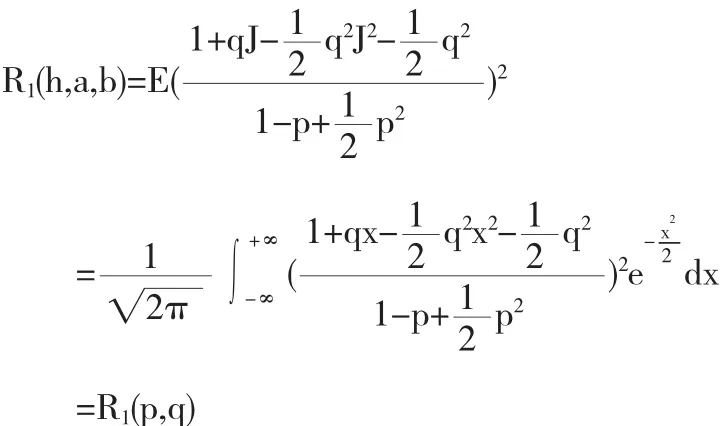
SIM2方法的均方稳定函数为：

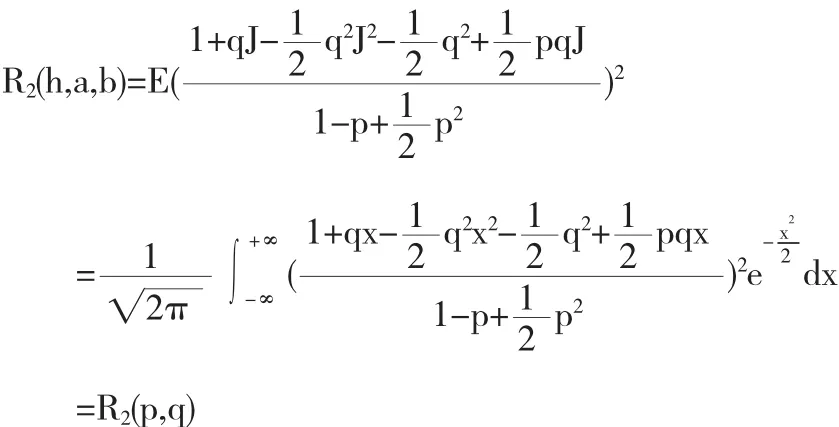
SIM3方法的均方稳定函数为：

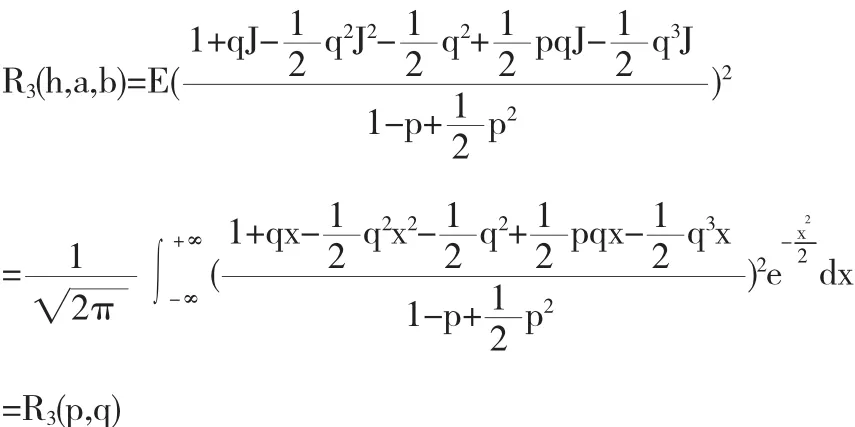
三种方法和其它几种方法（Euler方法[4]，Milstein方法[5]，半隐式Milstein方法[6]）的均方稳定域比较如下图1，图2，图3所示.

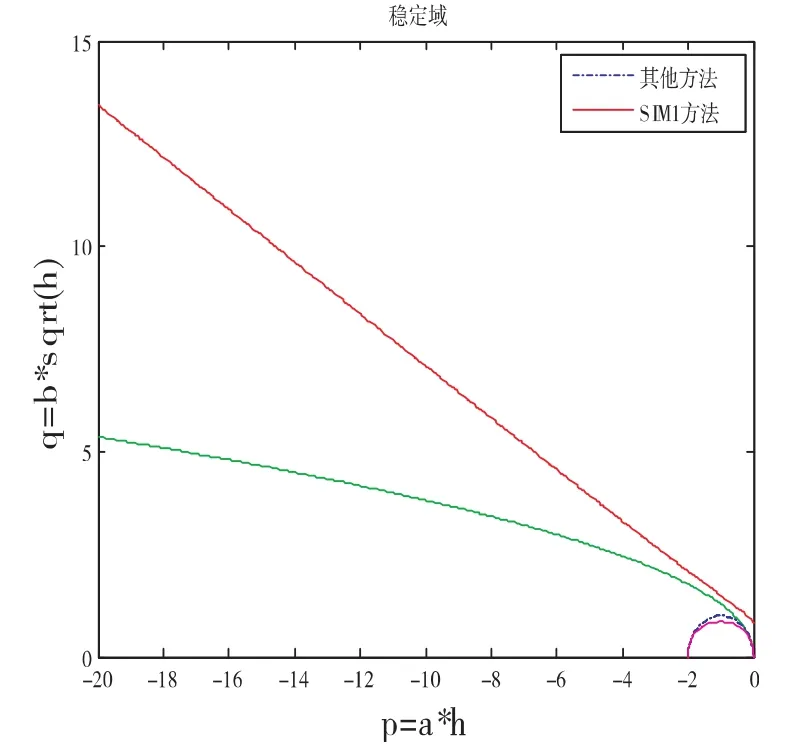
图1 （SIM1方法）

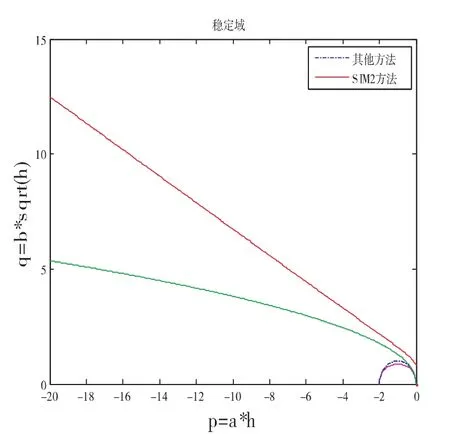
图2 （SIM2方法）

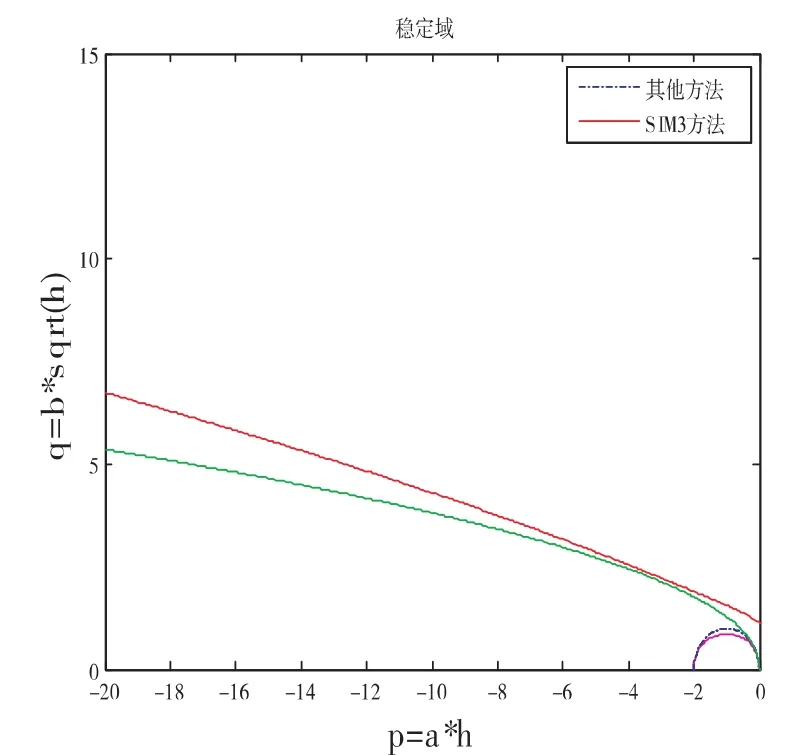
图3 （SIM3方法）

通过上述三个图发现，SIM1方法，SIM2方法，SIM3方法均比其它几种方法的稳定域要大，尤其是SIM1方法与SIM2方法的稳定域均远大于其它几种方法.

3 精度比较

在线性试验方程（5）中，令a=-10，b=7，仍将这几种方法的稳定域与上述其它几种方法的精度（全局平均误差）进行比较，比较结果如下表1所示：

表1

从上表看出，三种方法的精度要优于Euler方法，总体上和Milstein方法基本相当，比半隐式Milstein方法略差，但其稳定性要远优于Milstein方法与半隐式Milstein方法.

4 数值解与精确解的路径比较

在线性试验方程（5）中，令a=-10，b=7，将由这三种方法得到的数值解与精确解的路径比较如下图5～图6所示，选取步长h=2-7:

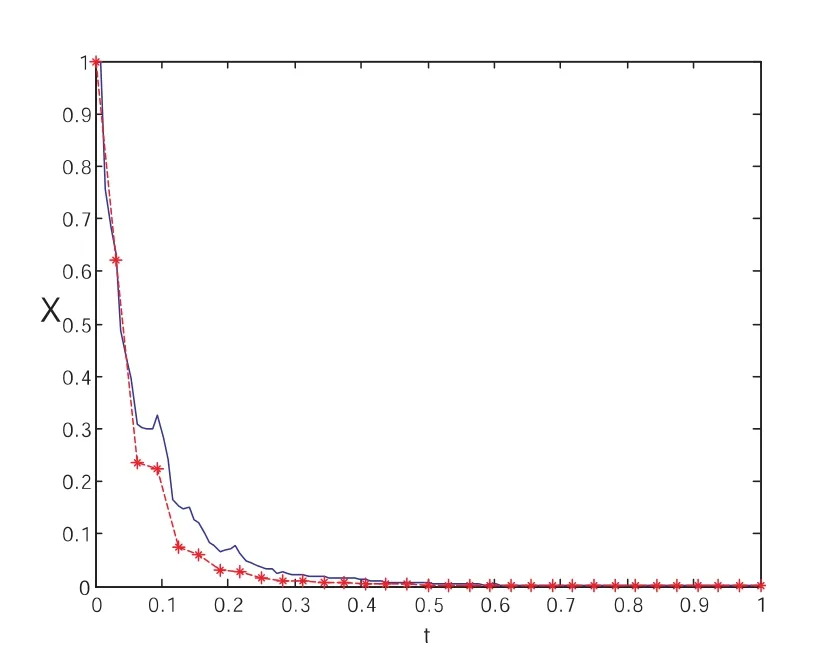
图4

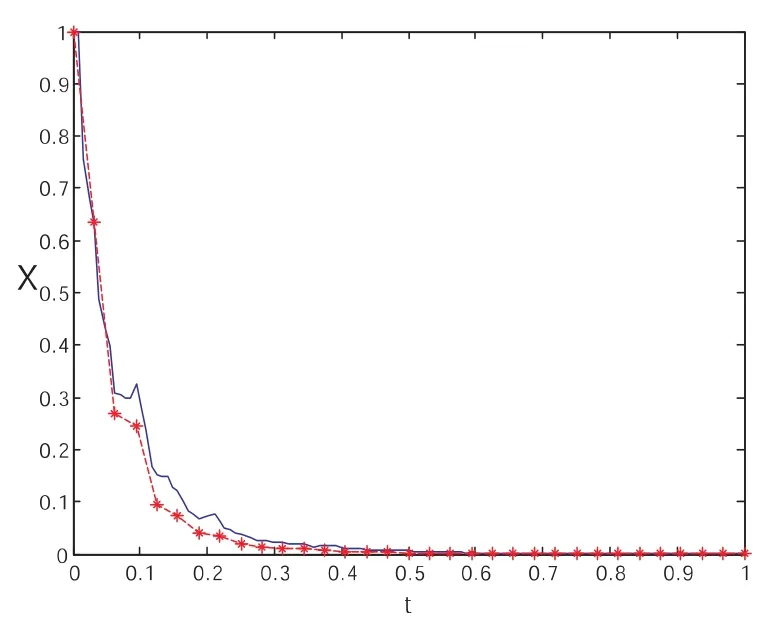
图5

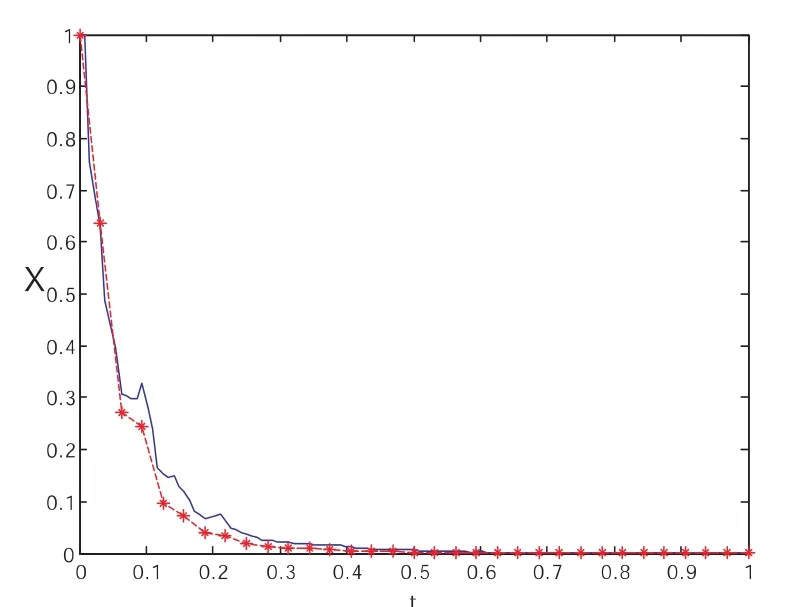
图6

从上图看出，三种方法的数值解与试验方程精确解的路径都具有较高的吻合度.