基于EGARCH-M模型的我国黄金期货价格波动性影响实证研究
2018-09-22姜忠鹤卢小广
闫 杰,姜忠鹤,卢小广
1.河海大学文天学院经管系,马鞍山,243031;2.河海大学商学院,南京,211100
2008年1月9日,上海期货交易所正式推出可交易的黄金期货合约,标志着我国黄金市场已开始与国际市场接轨。经过10多年的发展,我国黄金的生产量和消费量均已位居世界前列。随着我国黄金市场的全面开放,影响黄金市场价格的因素也逐渐增多。国际上,欧洲的债务危机、美国的次贷危机、石油价格的波动、政治动荡、美元贬值、全球的经济前景不明朗等导致我国黄金价格波动。国内通货膨胀的压力加大、股市大幅震荡、房价有效调控等,使得越来越多的投资人在国内掀起了黄金投资热潮,他们想通过购买黄金来实现资产的保值、增值,促使黄金价格屡创新高。但是,黄金价格的剧烈波动也让很多投资人遭受了巨大损失。因此,对我国黄金价格波动问题进行研究,探讨金价波动的特征,对未来黄金价格的走势进行预测,对个人投资者和机构投资者都有重要参考价值,同时也为黄金期货市场稳定健康发展提供借鉴。
1 问题的提出
陆国庆等采用GARCH族模型对美元指数和黄金价格分别进行分析,在此基础上建立了DCC-GARCH模型来分析两市场间的动态关系,研究结果表明,美元指数与黄金价格在长期内具有一定的负相关关系[1]。徐庆娟等以上海黄金交易所Au99.95的黄金现货收盘价为研究对象,建立了ARMA(2,1)-GARCH(1,1)模型,比较t分布下和GED分布下的拟合模型,发现基于t分布的GARCH模型更适合解决黄金期货对现货的影响问题[2]。曹辉以上海期货交易所的黄金期货价格为研究对象,构建了GARCH族模型来检验我国黄金期货市场的价格波动特征,研究结果表明,当分别引入黄金期货的交易量和持仓量时,无论在当期还是滞后期交易量对价格波动的影响都十分显著[3]。张延利等利用 GARCH(1,1)模型所具有的良好的非线性和异方差特征、马尔科夫链的动态变化特点,结合动态数据驱动预测原理,建立了GARCH-马尔科夫模型[4]。关于此类相关研究的还有赵崇增等[5-7]。
从相关文献可以看出,国内学者对黄金期货价格的研究多集中在黄金收益率、黄金期货市场与其他金融市场的关系等方面,关于黄金期货价格波动的研究比较少。本文在以上研究的基础上,考虑波动项对黄金期货价格的影响,利用GARCH族系列模型拟合黄金期货价格的波动影响模型,经过对比及调整,最终得出EGARCH-M模型能更好地拟合黄金期货价格的波动情况。
2 理论模型及数据来源
分别采用GARCH、 GARCH-M和EGARCH-M模型来刻画黄金期货价格波动性特征,研究这一波动性对黄金期货价格的影响。
2.1 GARCH模型
GARCH模型的基本形式如下:
yt=c+βxt+εt
(1)
(2)
(3)
式(1)为均值方程,yt是因变量(黄金期货价格),xt是自变量(黄金现货价格),xt还可以是因变量的滞后项或其他外生变量。本文取黄金期货价格为被解释变量,黄金现货价格为解释变量。β为代估参数向量,εt为误差项。
式(2)中,ht是εt的条件方差,随机变量vt可以假定服从N(0,1)分布,而且这一变量中的子序列为独立同分布序列,此时的模型为正态GARCH模型。随机变量vt亦可以假定服从T(0,1)分布,或者GED分布等其他分布。
2.2 GARCH-M模型
在金融市场上,投资者对金融产品价格涨跌的预期风险也会影响金融产品未来价格的走势[8],为了度量预期风险对收益率的影响,Engle等在1987年提出,在GARCH模型的均值方程的自变量中加入条件方差(即方差的某种函数形式)[9],用来刻画金融产品时间序列受自身条件方差的影响,得到的GARCH-M模型如下:
yt=c+βxt+γf(ht)+εt
(4)

2.3 EGARCH模型
虽然GARCH模型可以很好地对金融产品时间序列的波动集聚及厚尾现象进行刻画,但GARCH模型对正负扰动的反应是对称的,而金融产品的实际价格波动往往是非对称性的。为克服此弱点,在GARCH模型的基础上,Nelson在1992年又提出了EGARCH模型。该模型将条件方差取对数以保证方差取值为正,使模型更加稳定,而且不需要对参数附加任何限制条件,求解过程更加灵活简单。EGARCH模型的方差方程为:
(5)
式(5)中,θ值相当于GARCH模型中除常数项之外的其他系数之和,反映黄金期货价格的波动程度,取值越接近于1,黄金期货价格波动的聚集性和持续性就越强。φ值反映非对称性,φ显著不为0,表明黄金期货价格波动对市场信息冲击的反映是非对称的;φ>0,表示市场上有关价格下跌的信息(负向冲击)对黄金期货价格波动的影响小于市场上有关价格上涨的信息(正向冲击)对黄金期货价格波动的影响;φ<0,表示黄金期货市场信息正向冲击对黄金期货价格波动的影响小于负向冲击对黄金期货价格的影响[10],该现象称为“杠杆效应”,φ为“杠杆效应”系数。
2.4 EGARCH-M模型
EGARCH(p,q)-M模型由GARCH-M模型的均值方程和EGARCH模型的方差方程结合产生,基本形式为:
yt=c+βxt+γf(ht)+εt
(6)
(7)
(8)
其中,随机变量vt默认服从N(0,1)分布,此时的EGARCH-M模型为标准正态模型,也可以假设随机变量vt服从t(学生)分布或GED(广义误差)分布。误差项εt也同样服从t(学生)分布或GED(广义误差)分布,此时的EGARCH-M模型是非正态模型。因为金融产品时间序列数据的分布形态大多是“尖峰厚尾”型,而前人的研究结果表明,厚尾分布(例如t分布)下的GARCH相关模型更适合用来刻画金融产品时间序列数据的波动性。
2.5 样本及数据来源
本文选取上海期货交易所2008年1月9日至2018年1月16日黄金期货价格10年来的日频数据[11]。利用滚动展期的方法选取比较活跃的期货合约(Au9995)的每日收盘价格作为黄金期货价格,记为GF,有效避免了到期期货合约价格波动较大、成交量小的现象。选取上海黄金交易所的AU(T+D)合约的每日收盘价格作为黄金现货价格,记为GA。在整理数据时,剔除2008年1月9日至2018年1月16日期间数据缺失的部分后,黄金期货价格和黄金现货价格分别整理出2 434个有效样本数据。文中数据来源于同花顺iFinD数据库,数据处理软件为EViews 6.0。
本文选取上海期货交易所的黄金期货合约(Au9995)和黄金现货(AU(T+D))为研究对象,是因为两个合约在上海期货交易所的交易比较活跃,而且已有研究表明,在比较成熟的期货市场中,通过期货交易所形成的期货价格能够比较真实地反映对应商品价格未来的波动趋势。此外,黄金期货合约(Au9995)1年有260个左右的观察值,满足GARCH族模型要求数据具有较多观察值的要求。
3 ARCH效应检验
构建以黄金现货价格为解释变量、黄金期货价格为被解释变量的拟合黄金期货价格回归模型,该回归模型的残差图,如图1所示,黄金期货价格波动在一些时期较小,在其他一些时期较大,存在波动“成群成堆”的聚集现象,误差项具有明显的条件异方差性特征。
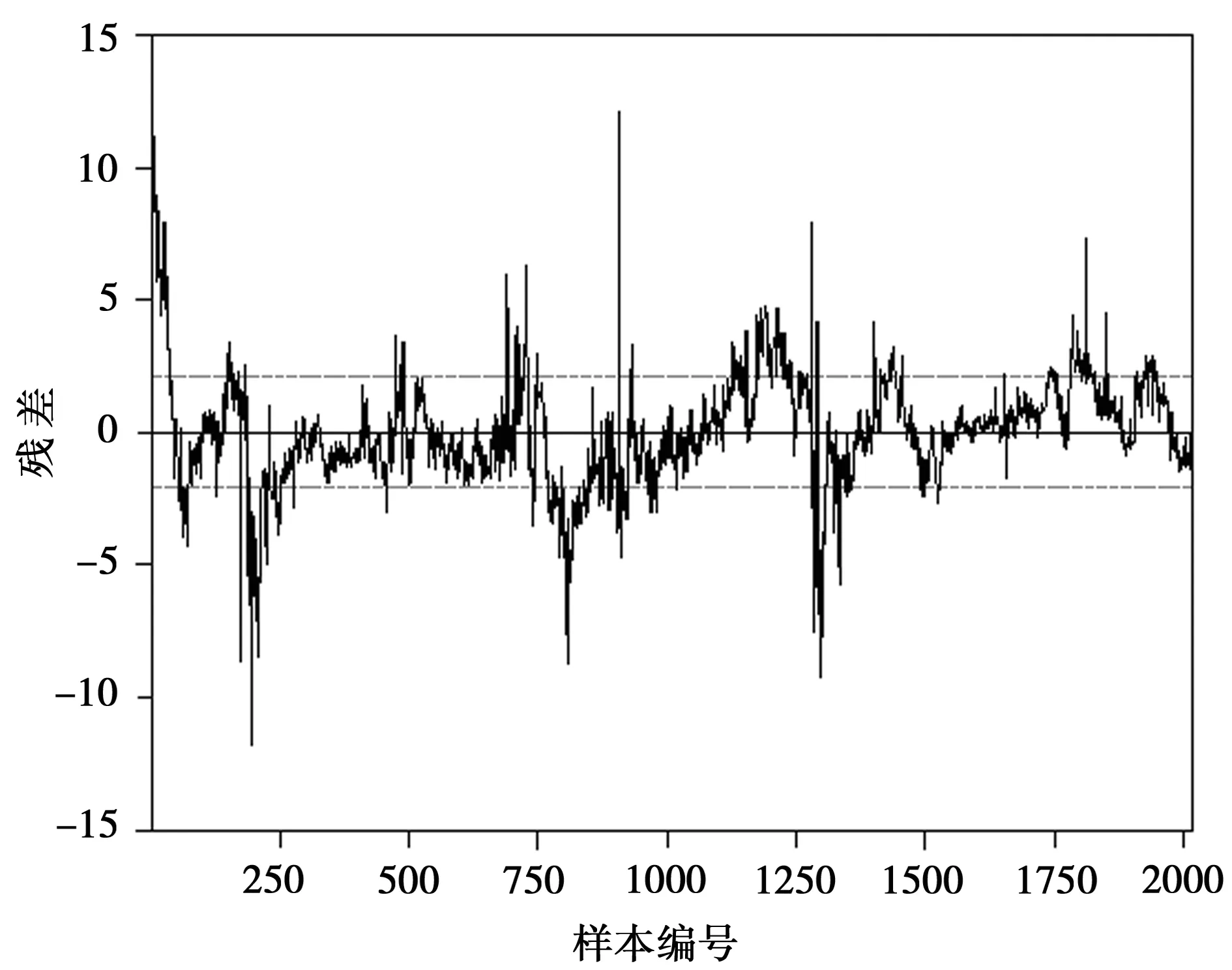
图1 黄金期货价格回归方程残差图
进一步对以黄金期货价格为被解释变量、黄金现货价格为解释变量的黄金期货价格回归模型进行ARCH LM检验,以检验回归模型的条件异方差性。表1为滞后阶数p=3阶时的ARCH LM检验结果。

表1 黄金期货价格回归模型条件异方差的ARCH LM检验表
检验结果表明,F统计量和LM统计量的伴随概率均趋近于0,显著小于0.05,表明在5%的置信水平下,ARCH效应检验都是显著的,黄金期货价格存在着显著的异方差性,并且存在着显著的高阶ARCH效应,适合采用GARCH族模型来进行拟合。
4 实证分析
由ARCH效应检验可知,黄金期货价格存在显著的高阶ARCH效应及异方差性,适合应用GARCH族模型拟合黄金期货价格的波动特征及其对黄金期货价格的影响。首先,使用典型GARCH(1,1)模型来拟合黄金期货价格的残差序列的条件异方差性[12],再根据拟合的模型结果逐步使用GARCH族的其他模型提高拟合效果。
4.1 GARCH(1,1)模型
本文先用GARCH(1,1)模型来刻画残差序列的条件异方差性,即构建GARCH(1,1)模型,可以得出估计的均值方程和方差方程:
GFt=-0.841 780+1.008 094GAt+εt
(9)
z=(-9.055 89) (2 841.57)
(10)
z=(9.887 99) (12.04) (29.277 7)
P=(0.000) (0.000 0) (0.000 0)
R2=0.998 37,对数似然值=-4 033.04,AIC=3.318 02,SC=3.329 93,D-W=0.273 01
4.2 GARCH(1,1)-M模型
GARCH(1,1)-M模型中的随机变量和误差项可服从正态分布、t(学生)分布或GED(广义误差)分布,每一种分布拟合的结果不同。本文首先假定均值模型的误差项服从正态分布,根据拟合的结果再作进一步分析。
4.2.1 假定εt服从正态分布
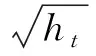
GARCH(1,1)-M估计得到的均值方程和相应的方差方程的结果如下:
GFt=-1.175 247+1.008 724GAt
(11)
z=(-12.209 23) (2 586.896)
(3.358 412)
(12)
z=(11.366 97) (11.769 57) (27.265 09)
P=(0.000) (0.000 0) (0.000 0)
R2=0.998 408,对数似然值=-4 029.92,AIC=3.316 28,SC=3.330 57,D-W=0.280 38
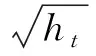
4.2.2 Jarque-Bera正态性检验
以上建立的GARCH(1,1)-M模型的假定条件是均值模型的残差项服从正态分布。如果残差项不服从正态分布,则在正态分布假设条件下建立的GARCH(1,1)-M模型的有效性值得怀疑。因此,需要检验黄金期货、现货价格及均值方程中误差项三个序列是否服从正态分布。由于本文所研究的样本容量较大(n=2 434),所以可使用以最小二乘估计(简称OLS)的残差为依据的Jarque-Bera(JB)检验方法,对黄金期货价格、黄金现货价格以及GARCH(1,1)-M模型的均值方程中误差项为正态分布进行假设检验,误差项时间序列用GARCH(1,1)-M模型中的残差项表示。JB统计量为:
(13)
式(13)中,S和K分别表示偏度和峰度。在正态分布的假设条件下,JB统计量服从自由度为2的x2分布。如果是原始数据,则k=0;如果序列是通过模型估计得到的,则k为估计的参数个数[10]。表2为正态性检验结果。

表2 Jarque-Bera正态性检验结果
由表2可知,GF和GA的偏态系数(S值)均大于0,峰度系数(K值)均小于3,所以GF和GA数据分布相对于标准正态分布是平坦的,且向右拖尾。GARCH(1,1)-M模型中的残差项的偏态系数(S值)大于0,峰度系数(K值)大于3,所以残差项数据分布的凸起程度大于标准正态分布,且向右拖尾。由描述性统计分析的各项数据可知GF、GA和GARCH(1,1)-M模型中的残差项均不符合正态分布的特征。GF、GA和残差项的JB检验统计量的伴随概率均趋于0,所以拒绝GF、GA和误差项服从正态分布的零假设,这表明GF、GA和误差项均不服从正态分布。
4.2.3 假定εt服从t分布
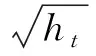
GFt=-1.283 79+1.008 876GAt
(14)
z=(-12.237 6) (2 558.77) (4.129 9)

+0.558 444ht-1
(15)
z=(6.592 2) (9.358 5) (17.499 2)
P=(0.000 0) (0.000 0) (0.000 0)
R2=0.998 412,对数似然值=-3 987.340,AIC=3.282 12,SC=3.298 79,D-W=0.281 95 T-DIST.DOF=15.949 60(P=0.000 0)
T-DIST.DOF项显著,说明误差项符合t分布假定。AIC和SC的值均小于与GARCH(1,1)-M模型(正态分布)对应的值,说明假定误差项符合t分布时所作的模型拟合度优于假定误差项符合正态分布时的GARCH(1,1)-M模型。D-W值为0.307 322>0.280 38,从变量的自相关性方面评价,t分布的GARCH(1,1)-M模型优于正态分布的GARCH(1,1)-M模型。
假定εt服从t分布,拟合GARCH(1,1)-M模型的D-W值明显小于2,说明该模型依然存在较大的序列相关性,需进一步改进。
4.3 EGARCH(1,1)-M模型
为了消除序列相关性,并进一步探明黄金期货市场的利空消息和利好消息是否对市场上投资者的个体投资行为产生不同的影响,即黄金期货价格波动性是否存在非对称“杠杆效应”问题,选择使用EGARCH(1,1)-M模型进行估计。
利用EGARCH-M模型估计判断利空和利好消息对黄金期货价格波动产生的非对称效应, 得到均值方程和方差方程估计结果如下:
GFt=-75.432 28+1.027 709GAt
(16)
z=(-1.678 413) (356.335 8) (18.167 18)
ln(ht)=0.181 504+0.978 163ln(ht-1)
(17)
z=(4.539 499) (319.425 9)
(-1.182 357) (17.303 12)
P=(0.000 0) (0.000 0) (0.237 1)
(0.000 0)
R2=0.999 643,对数似然值=-2 404.388,AIC=1.982 242,SC=2.001 296,D-W=2.056 029
EGARCH-M模型与t分布的GARCH(1,1)-M模型相比,对数似然值有所增加,同时AIC和SC的值都变小了,说明EGARCH-M模型能更好地拟合数据。
4.4 GARCH族模型参数估计对比分析
为直观地比较4种模型计算拟合黄金期货价格的总体情况,表3为分别运用GARCH(1,1)模型、正态分布的GARCH-M模型、t分布的GARCH-M模型和t分布的EGARCH-M模型的拟合结果。
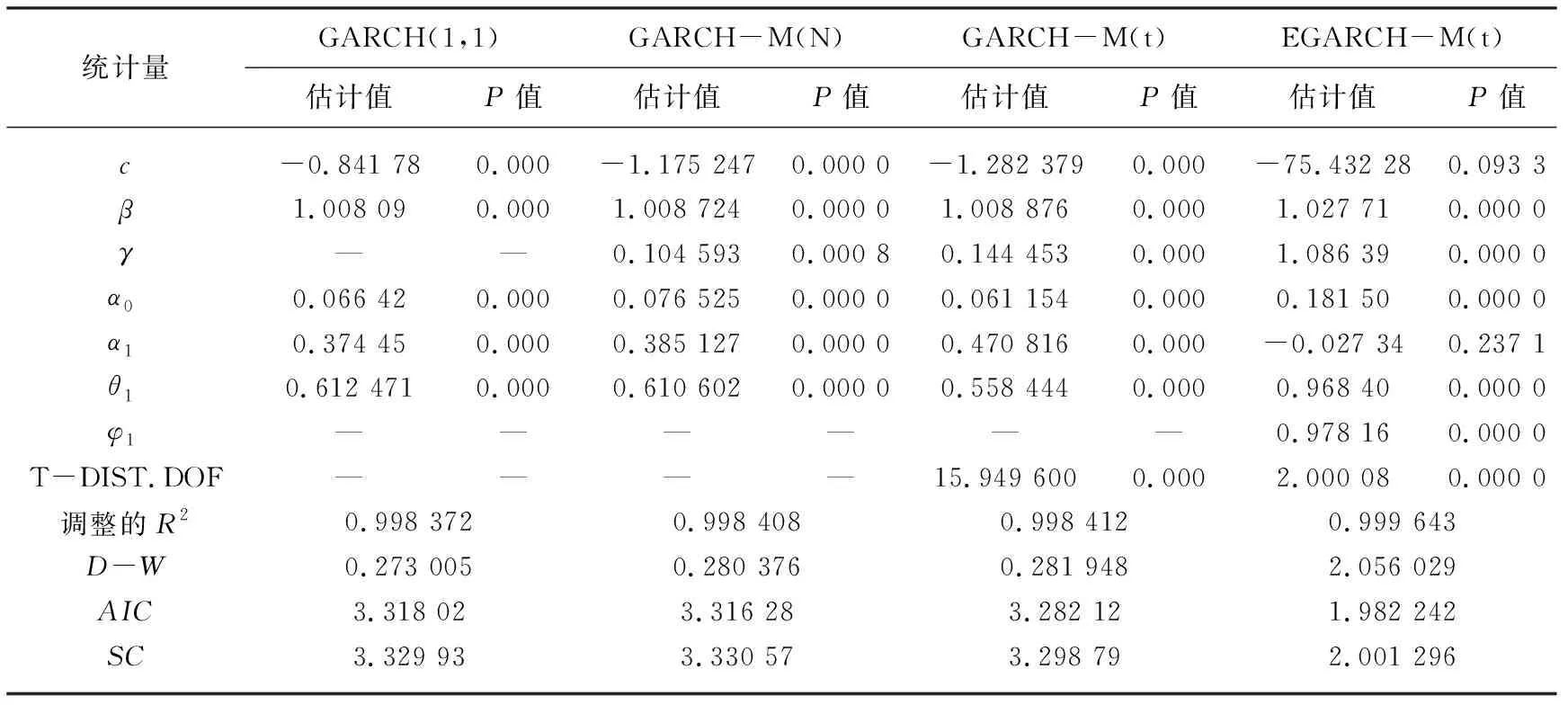
表3 GARCH族模型参数估计及其显著性检验分析表
由表3的GARCH族模型参数估计及其显著性检验结果可以看出,4种模型的θ1系数均显著为正,而且各系估计值都比较大,表明过去时期黄金期货价格的波动对其后期波动的影响是正向边际递减的,即黄金期货价格的波动有聚集性特征。均值方程中的参数γ在GARCH-M(N)、GARCH-M(t)和EGARCH-M(t)3种模型中都是显著为正的,说明我国黄金期货市场的风险与收益存在正相关的关系,即存在风险溢价现象[13]。从方差方程上看,4种模型的回归系数α1与θ1之和均接近于1,表明黄金期货市场在某时刻的收益冲击具有持续性的影响,波动率的衰减较慢,波动性具有持久性和长记忆性。从杠杆效应的拟合上看,4种模型的参数均大于0,在5%显著性水平下均显著,表明黄金期货价格存在明显的杠杆效应。
从调整的R2、D-W值、AIC值、SC值等数据对比来看,EGARCH-M模型能更好地拟合黄金期货价格的波动情况。
5 结 语
本文采用上海期货交易所2008年1月9日至2018年1月16日期货合约(Au9995)和现货(AU(T+D))合约的日收盘价格为研究对象,对黄金期货价格的波动性及其对黄金期货价格的影响进行实证研究。

根据以上结论,建议我国应加强对黄金市场的监管,监管机构应探索与国际惯例接轨、与市场经济相适应的新的监管方式。对黄金市场商品准入标准、黄金市场主体的准入标准、资质和行为规范、黄金市场的运行规则等环节进行有效监管,减少因黄金期货价格的波动给投资主体带来的不利影响。我国黄金期货市场应做好防范资本市场冲击所带来的风险,合理应对黄金市场上利空与利好信息的不对称冲击,以减少由黄金市场信息刺激所带来不合理的黄金期货价格上的涨跌,并提前制定应对机制,做好防冲击的应对工作。
