基于误差迭代的旋转机构偏心测量

陈 斌 张 洋 郭 贤 高德伟 高建树

中国民航大学航空地面特种设备研究基地，天津，300300

0 引言

采用旋转机构的设备广泛应用于航空航天、电力、石化、冶金、煤炭、核能等行业，是国民经济支柱产业中的重要设备，旋转机构的故障或非正常运行容易导致严重的生产和安全事故［1］。转子系统是旋转机构的核心部件，承担着旋转机构的主要功能，而旋转机构的故障大多由转子系统引起［2］。因此对旋转机构转子系统故障机理和故障诊断进行研究显得非常重要。

对转子振动偏心信号的研究是旋转机构故障诊断的重要手段之一。转子振动偏心过大会导致系统产生交变应力，对设备的稳定运行造成不利影响［3⁃4］。目前，对于振动偏心信号的监测，一般采用先对信号整周期采样，再进行频谱分析的方法来实现［5⁃7］。国内外学者对信号的整周期采样进行了大量的研究，并取得一系列丰硕成果。胡劲松等［8］提出了应用微分和样条插值的转子振动信号同步整周期重采样方法。陈曦等［9］采用同步采集转速信号与振动信号的方法，通过软件实现整周期采样。李伟等［10］基于本特利408数据采集系统，采用双坐标测量法得到不同速度下混流泵转子X、Y方向频谱图，对轴系振动状态进行了研究。REN等［11］提出了一种基于泰勒级数展开和傅里叶算法的混合方法，使用动态信号模型方法进行周期估计，实验证明该方法优势明显。KASHIWAGI等［12］介绍了使用光脉冲合成器（OPS）来测量频率的方法，通过构造单相滤波器对信号进行滤波来获取信号的周期。

实际应用中，文献［8⁃10］的方法需要同步采集两路信号，信号采集的实时性很难保证，且对采集设备要求较高，容易导致非整周期采样的谱泄露和栅栏效应。文献［11⁃12］采用的模型复杂，应用约束条件多，实际使用受限。为克服以上缺点，本文利用单路传感器信号特征，对振动信号在时域内进行特征提取和整周期采样，提出基于误差迭代的旋转机构偏心测量方法，开发出基于LabVIEW的故障诊断系统，以飞机襟翼驱动器输入驱动系统为模拟测试对象，验证该方法的准确性。

1 转子偏心测量方案

1.1 转子-感应器-传感器系统物理模型

为实现对转子偏心参数的测量，本文提出一种在转子上加装六边形感应器（以下简称感应器），通过对传感器信号周期测量值与理论值的分器系统如图1所示。充磁后的环形磁钢1（通过布置在转子轴承上的磁钢座法兰与转子同轴安装）提供系统工作所需磁场；传感器2为磁电式转速传感器，通过安装架固定于传感器端面，距感应器突出部1 mm处；感应器3由导磁性良好的材料制成，被压入转子4的上端。感应器跟随转子在环形磁钢产生的磁场中旋转，引起传感器线圈气隙磁通的变化，并感应出交变电压信号。转子材料密度不均匀、加工缺陷、安装过程的撞击、运行过程的离心膨胀与热变形等都会导致转子质量不平衡［13⁃14］，转子的几何中心一旦偏离其旋转中心，就会引起转子偏心，导致感应器偏离原来位置，传感器输出信号相应发生变化，按照信号变化的大小，可以确定出转子的偏心值。

图1 转子-感应器-传感器系统物理模型Fig.1 Rotor”hexagonal sensor-sensor system physical model

1.2 感应器数学模型

1.2.1 感应器工作机理

截短的感应器质量分布不均匀，加装该感应器破坏了转子的平衡结构，在对转子-感应器系统动平衡后，系统依旧存在剩余不平衡量［15］。如图2所示，感应器2一旦跟随转子旋转起来，其旋转中心4就会偏离几何中心5，在电磁转速传感器3中感应出交变电压信号，同时，转子在径向产生偏心［16］，用b、α分别表示偏心距和偏心角。

图2 感应器数学模型Fig.2 Sensor mathematical model

感应器旋转时，六边形感应器由于交变电流而产生交变磁场，使得穿过磁电转速传感器的磁通量变化，导致磁电转速传感器中产生正弦交流电压信号，其中，每边产生1个正弦信号，感应器旋转一周形成6个交流电压信号，在这里用Ti={T1，T2，…，T6}表示信号的周期，下标i表示每边在空间所处的位置。截短突出部的存在使得截短绕组中的2个电压信号幅值有别于其余4个。

借助现代电子测量技术测得6个正弦信号周期的测量值Tmi={Tm1，Tm2，…，Tm6}，该周期理论值用Tci={Tc1，Tc2，…，Tc6}表示。每边逆时针旋转过的角度（以下简称旋转角）用 θi={θ1，θ2，…，θ6}表示。则每边对应的正弦信号周期理论值为

式中，Ta为测量得到的感应器从一个突出部旋转至另一个突出部对应时间的平均值。

1.2.2 旋转角与旋转中心坐标的耦合关系

假设感应器旋转角θi与转子旋转中心坐标（x，y）满足关系式：

根据感应器数学模型，式（3）可转化为

式中，R为感应器突出部未截短时的感应器内切圆半径。

1.2.3 周期理论值与旋转中心坐标的耦合关系

根据旋转机械运行实践，假设旋转中心坐标（x，y）满足关系式：

式中，L为旋转中心存在范围的宽度，根据实际来确定。

以转子的几何中心为坐标原点建立直角坐标系，在式（5）表示的区域内令沿OX、OY轴方向的步长分别为Δx、Δy，且Δx=Δy=u，以坐标原点为起始点，分别沿X、Y轴方向，对整个区域进行搜索，得到足够多的待计算旋转中心坐标（x，y）。

将式（2）、式（4）代入式（1）即可得到周期理论值Tci与转子旋转中心坐标（x，y）的关系方程组：

Tci=3Taθi/π i=1,2,…,6 （6）

综上，通过对转子-感应器-传感器系统物理模型的分析，根据感应器的工作机理即可确定传感器输出信号周期的理论值Tci，进而建立偏心测量的理论模型。

2 基于误差迭代的偏心求解算法

通过对周期测量值Tmi与理论值Tci的误差分析，提出了基于误差迭代的转子振动偏心参数求解算法，实现步骤如下：

（1）计算周期测量值Tmi与理论值Tci的绝对误差。通过对周期测量值Tmi与理论值Tci的误差分析可得：

式中，Δi为Ti周期的周期测量值与理论值的绝对误差。

将六边形绕组感应器跟随转子旋转一周区分出的6个周期的测量值与理论值的绝对误差求和：

式中，Δsi为转子旋转一周周期测量值与理论值的绝对误差和。

（2）计算转子实际旋转中心坐标。将按照步长u取到的每一点可能的旋转中心坐标（x，y）代入式（6），再根据式（7）、式（8）对每一点对应的绝对误差和迭代值进行比较，Δsi最小时，偏心存在区域内该点使得转子旋转一个周期的测量值与计算值最接近，该点与转子真正旋转中心最接近，则对应的坐标（x，y）即为转子实际的旋转中心坐标。

（3）计算转子偏心参数。根据步骤（2）得到的转子旋转中心坐标（x，y），依据图2感应器的数学模型，可分别求得转子的偏心距b、偏心角α与转速n：

式中，fs为信号采样频率。

通过对周期测量值与理论值的误差迭代分析即可得到转子实际旋转中心坐标，进而按照转子偏心测量理论模型得到转子偏心参数。

3 系统软件设计

3.1 系统的软件实现

测试系统基于LabVIEW 2016专业版软件开发，采用生产者/消费者的程序设计模式［17⁃18］，系统的设计流程如图3所示。

图3 设计流程图Fig.3 Design flow chart

测量软件的编制主要依据具体测试任务，按照测量的流程依次进行。旋转机构偏心参数的测量主要有两个过程：①根据传感器输出信号波形幅值特征设计算法，确定转子旋转中心坐标；②由转子旋转中心坐标，依据偏心测量理论模型实现偏心参数的测量。

3.2 整周期采样算法

旋转机构偏心测量的关键在于对振动信号的整周期采样。基于微分及样条差值的整周期采样算法在对转速脉冲信号进行微分放大的同时将干扰放大，因此对于有干扰的键相信号该方法并不适用，特别是当振动信号的幅值接近键相信号的幅值时，会导致以键相信号幅值进行判断的整周期采样方法出错；键相传感器每次在键相槽采集的位置是随机的，会导致振动信号的相位产生零点漂移误差，因此必须找到更好的整周期采样方法。

基于误差迭代的偏心测量算法实现的关键是对周期测量值Tmi的准确测量，这种测量需要借助对传感器输出信号的整周期采样来实现，图4为传感器输出信号。

图4 传感器输出信号Fig.4 Output signal of the sensor

该算法不依赖键相信号，根据单路振动信号幅值特征来确定整周期采样的起止点a0、a6，周期测量的起止点对应信号的上升沿过零点，数据采集卡采集数据时，往往不能采集到所有的上升沿过零点，因此需要借助插值法来获取该点。基于La⁃grange插值算法实现信号整周期采样的步骤如下。

3.2.1 基于Lagrange插值算法确定上升沿过零点

Lagrange插值算法根据信号前后两个时刻的采样值来判断信号是否为上升沿过零点，若前后两个时刻信号采样值的乘积为负数，且前一时刻信号采样值为负数，则判断其为上升沿过零点［19］。根据Lagrange插值多项式：

当P(t)=0时，可以求得上升沿过零点位置：

3.2.2 基于信号幅值特征实现整周期采样

如图4所示，a0、a6为转子旋转一周整周期采样的起止点，a6点也是下一周期采样的起始点，这两点所在周期的幅值要比其余4个周期的小，依据这一特征，通过计算机编程的方法即可确定周期测量的起止点的位置，再根据信号采样频率fs,由公式

即可依次求取周期的测量值Tmi，在时域内实现对振动信号的整周期采样。

基于单路振动信号幅值特征可实现对整周期采样起止点的准确捕获，降低了对数据采集设备的要求；将经过数据采集卡平滑滤波后的振动信号周期测量值多个周期取平均，避免测量数据跳跃等不稳定现象，有利于振动信号的精确分析。

4 实验与测试

4.1 测试平台的搭建

如图5所示，系统的硬件部分由磁电式转速传感器、NI⁃TB2708模块、NI⁃PXI6115数据采集卡、北京航天测控技术有限公司AMC58222 PXI智能平板等组成。磁电式转速传感器的信号输出口与NI⁃TB2708模块的AI0端口通过射频连接器传递转子偏心产生的振动信号；NI⁃TB2708模块与PXI⁃6115数据采集卡通过SMB接口连接；采集卡与平板电脑以PXI插槽的方式连接。

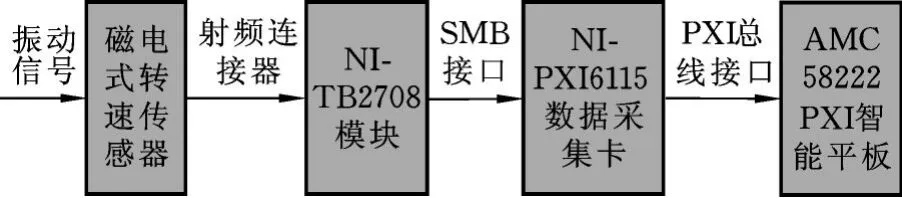
图5 系统硬件组成Fig.5 Hardware composition of the monitoring system

4.2 测试过程及结果分析

4.2.1 测试过程

为验证转子偏心求解算法的可行性，在襟翼驱动器输入驱动轴转速分别为390 r/min、450 r/min、510 r/min时，对输入驱动轴转子的振动参数进行实时监控。

测试开始前需要参照偏心存在区域范围L，依据式（8）～式（10），在0～1的范围内，确定迭代步长u的数值，设定襟翼驱动器输入驱动轴转速1 650 r/min的条件下，得到偏心距b、偏心角α、绝对误差和的最小值Δsmin与步长u的关系曲线。

由图6可知，步长u在0～3µm范围内，转子偏心参数稳定，绝对偏差和的最小值为4.91×10-10m；步长大于3µm后，待计算旋转中心坐标（x，y）过少，稳定工况下偏摆参数出现较大波动。本测试中考虑到采集设备硬件条件，取步长u为1µm。

图6 偏心参数随步长变化曲线Fig.6 Curve of eccentricity parameter changes with step length

测试系统参数设置如表1所示。测试系统的硬件平台与软件主界面如图7所示。

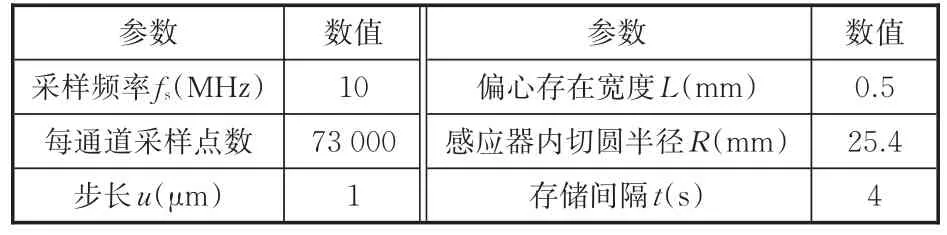
表1 测试系统参数设置Tab.1 Parameter settings of the test system

图7 监测系统平台Fig.7 Monitoring system platform

为验证测试结果的准确性，采用文献［10］中的双坐标测量法，在襟翼驱动器输入驱动轴周围垂直布置2个位移传感器，分别测量转子x、y方向的振动值，用x′、y′表示，由两位移传感器测量数据依据式（9）、式（10）推导出偏心距、偏心角分别用b′、α′表示，本系统与位移传感器的测试数据如表2所示。

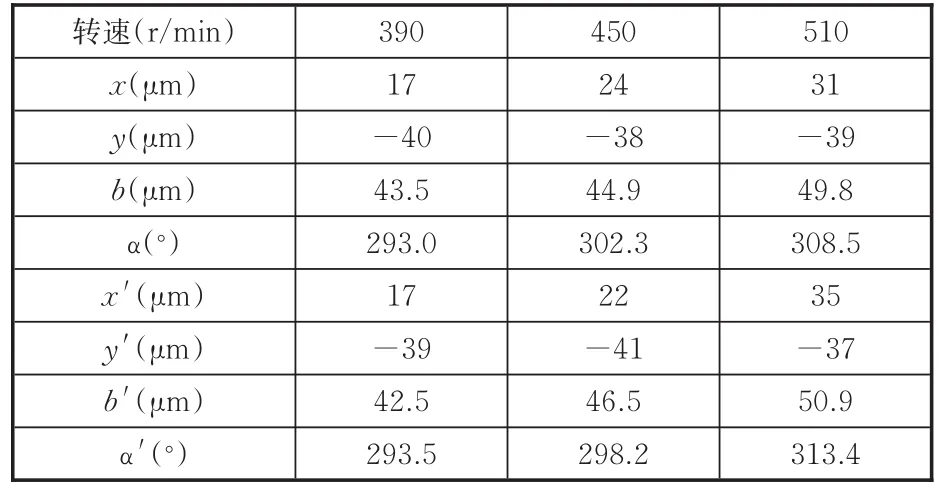
表2 不同转速下的测试数据Tab.2 Test data under different rotational speed

4.2.2 测试结果分析

由表2可知，与双坐标测量法相比，3种恒定转速下偏心距的测量误差分别为2.3%、3.5%、2.2%，最大误差为1.6µm，精度在微米级。对比3种转速下的偏心距可知，恒定转速下，转子偏心距基本维持不变；转速越高，转子旋转中心相对于几何中心偏离越大，偏心距随之增大，转子的振动越剧烈，与实际情况相吻合。实验表明：基于生产者/消费者程序设计模式采集系统可实时准确采集转子振动信号，并且实时刷新显示系统处理后的偏心参数，将数据按照设定的存储间隔保存到数据库，具有较高的可靠性、稳定性。

5 结论

基于转子-感应器-传感器系统的物理模型，分析了感应器的工作机理，根据单路传感器信号幅值特征，实现了时域内信号的整周期采样，建立了旋转机构偏心测量的理论模型，提出了对转子振动信号周期理论值与测量值进行误差迭代分析来测量旋转机构偏心参数的方法，最后采用生产者/消费者的程序设计模式在LabVIEW平台下实现了该方法。

利用该系统对3种恒定转速下襟翼驱动器输入驱动系统振动偏心参数进行了模拟测量，系统能够实时、准确地采集转子振动信号，能够实现海量数据的高速吞吐。验证了系统的可靠性、模型和测量方法的正确性。