利用有限制稳定配对策略求解双目标柔性作业车间调度问题

杨 宇 黄 敏 王震宇 朱启兵

江南大学物联网工程学院，无锡，214122

0 引言

柔性作业车间调度问题（flexible job-shop scheduling problem，FJSP）是指在并行机和多功能机并存的作业车间内，合理安排各工件工序的加工机器和作业时间，以实现给定的多性能指标优化［1］。FJSP包含了机器分配和工序调度两个问题，具有约束条件多、计算复杂度高等特点，属于典型的NP-hard问题［2⁃3］。FJSP 的求解策略一直是生产管理及组合优化领域的研究热点之一，具有重要的理论意义和实际应用价值。

FJSP需要对生产过程中的多个性能指标进行优化，由于各性能指标往往存在冲突，因此一般难以获得满足各性能指标、同时最优的FJSP全局解，仅能获得各性能指标最佳均衡的FJSP满意解，称之为Pareto最优解［4］。在实际运用中，FJSP往往需要获得一个分布广泛的Pareto最优解集合，供决策制定者根据其需要（对各性能指标的要求）加以选择［5］。多目标进化算法（multi-objec⁃tive evolutionary algorithm，MOEA）因其在解决FJSP时可获得一致性的Pareto最优解，已经成为解决此类问题常用的方法［6］。如何在保证解的收敛性的同时，获得具有广泛分布性的Pareto最优解集，是利用进化算法求解FJSP的关键［7］。张超勇等［8］采用带精英策略的非支配排序遗传算法（non-dominated sorted genetic algorithm，NSGA-Ⅱ）求解FJSP，获得的最优解较好，但会聚集在Pareto前沿附近的某一个狭小区域内，无法为决策者提供宽泛的选择，且计算代价较大。ZHANG等［9］针对连续型问题的特点，提出一种基于问题分解 的 MOEA（MOEA based on decomposition，MOEA/D），随后，CHANG等［10］使用 MOEA/D求解FJSP。MOEA/D算法将多目标优化问题分解为多个单目标优化的子问题，并采用子问题合作方式进行优化，取得了比NSGA⁃Ⅱ更佳的性能，但进化过程中存在的“超级解”会使解丢失，因此种群的分布性无法得到保证。为了解决“解丢失”的问题，LI等［11］将稳定配对思想引入MOEA/D，提出了基于稳定配对选择策略和分解相结合的MOEA（MOEA based on decomposition and sta⁃ble matching，MOEA/D⁃STM），此算法虽然可以避免解丢失，但在进化过程中，每一代选择到的解的收敛性优于多样性，这个缺点将影响Pareto最优解集的多样性和收敛性。

因MOEA/D⁃STM算法在解决连续性问题上的性能优于MOEA/D算法，且后者在解决FJSP时表现出了良好的性能，故本文将MOEA/D⁃STM算法引入到FJSP的求解中。针对传统MOEA/D⁃STM算法中配对选择策略缺乏约束限制带来的解的分布性能难以充分保证的缺点，提出了一种有限制的稳定配对选择策略和分解相结合的MOEA（MOEA based on decomposition and limited stable matching，MOEA/D⁃LSTM），以平衡进化过程中的收敛性和分布性，并提高Pareto最优解集的收敛性和分布性。通过标准测试集和实际车间生产实例来验证算法的有效性。

1 FJSP调度模型

FJSP可具体描述如下：n个待加工工件的集合 J={J1，J2，…，Jn}，工件在 u台机器上加工，机器集合M={M1，M2，…，Mu}，工件Ji包含ni（ni＞1）道工序，其工序集合Oi={Oi1,Oi2,…,Oini}。所有的工序按照制定的加工路线进行，工件Ji的第j（j=1，2，…，ni）道工序Oij可在多台机器上操作。调度的目标是为每一道工序确定一台机器，同时将机器上待加工工序做排序，使得系统的整体性能最优。本文研究的问题是一个有约束的双目标优化问题，即在满足所有约束条件的情况下，优化目标兼顾最小化最大完工时间和最小化总成本。

最小化最大完工时间定义如下：

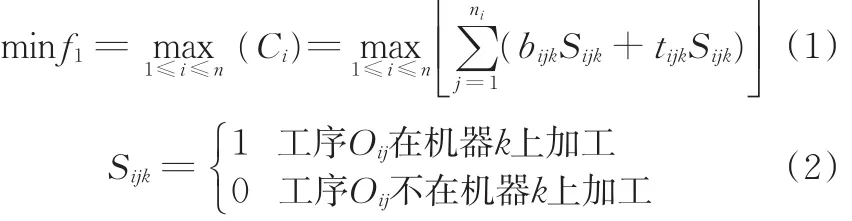
式中，Ci为工件i的完工时间；bijk为在机器k上开始加工工序Oij的时刻；tijk为使用机器k加工工序Oij所用的时间；Sijk确定Oij是否在机器k上加工。

（2）非经营性和准经营性资产管理部门。非经营性和准经营性资产管理部门主要负责提高这类资产的使用效率，保证非经营性资产和准经营性资产的安全和完整性，确保高校对这类资产使用的连续性。

（1）如果候选解xi∈X没有和任何子问题pt配对，则对于任意的子问题pt，其对当前的配对解Δp(pt,xi)；

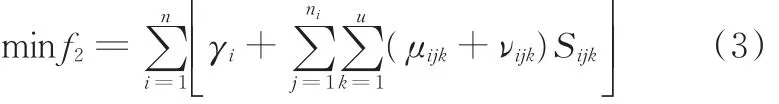
式中，γi为工件i的材料费；μijk、νijk分别为工序Oij在机器k上的加工费用及人工费。

约束条件：

（1）工序约束。工件各工序存在先后顺序，工序Oij必须在工序Oi（j-1）完成之后才可以开始加工，即

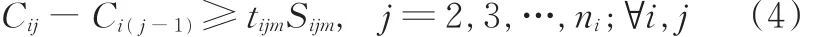
式中，Cij为工序Oij的完成时刻。

NAM模型模拟的安阳站日径流过程的精度比较结果详见表1。NAM模型模拟的日径流过程，在率定期内，确定性系数大于0.9，等级属于甲等的有2年;确定性系数大于等于0.7小于等于0.9，等级属于乙等的有5年。在验证期内，确定性系数都在大于等于0.7小于等于0.9的范围内，等级都属于乙等。径流深相对误差，在率定期内，5年都合格，合格率为100%；验证期内，3年都合格，合格率为100%。

（2）机器约束。同一台机器在同一时刻只能加工一道工序，在某时刻h(h＞0)，若Sijk=1则在i≠p 或j≠q条件下，Spqk≠1恒成立。

筛选自闭合微短等高线的关键是选择阀值，筛选时应考虑成图比例尺和测区地貌等因素。阀值越小，自闭合微短等高线删除越少；阀值越大，误删正常等高线的可能性越大。例如，对于1∶2 000地形图，直径2 mm以下的圆形等高线在图上难以辨认，可以舍去，其对应的实地周长约为13 m。因此可以选择13 m作为阀值，长度小于该阀值的等高线将被判定为自闭合微短等高线并删除。

（3）连续性约束。任何工序一旦开始加工，则不可被打断，即

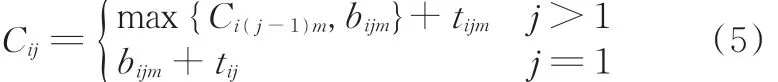
（4）除了满足以上约束条件外，还应该满足所有机器在h=0时刻可用，且所有工件优先级相同。

2 基于MOEA/D⁃LSTM算法的FJSP求解

2.1 MOEA/D”STM算法

MOEA/D⁃STM算法主要包括：①将一个多目标优化问题转化为多个单目标优化的子问题，并计算候选解集对子问题、子问题对候选解集的偏好矩阵；②基于偏好矩阵选择具有稳定配对关系的候选解子集；③对选择的候选解子集进行演化操作并重复步骤②，最终获得Pareto最优解集。

其中，g(·)为切比雪夫距离，z*=为参考点，且=fl(xi),l=1,2,…,m。

（3）算法停止。当g＞K时，满足停止条件，输出种群染色体,并解码成调度方案；否则，返回步骤（2）。

2.1.1 分解多目标优化问题，构建偏好矩阵

尽管原始的MOEA/D-STM算法可以在一定程度上保证选择的解在目标空间具有较好的分布特性，但是当原始的候选解集合在目标空间分布不均匀（具有聚集现象）时，其配对选择后的候选解在目标空间中仍然较为聚集，从而最终影响到候选解在目标空间的分布性。如图1a所示，原始的候选解x1、x2、x3、x4分布在p1和p2之间的区域 ，构 成{(p1,x1)，(p2,x3)，(p3,x4)，(p4,x2)，(p5,x10)}稳定配对关系，如果利用稳定配对关系进行选择，则x1、x2、x3、x4、x10将会被选择进入演化操作，从而影响选择的候选解在目标空间分布的多样性。产生这一问题的原因在于原始的MOEA/D⁃STM算法在计算子问题对候选解的偏好值时，没有对精英解的贪婪性进行限制。为此，本文引入一个限制算子，将子问题对候选解的偏好加以约束限制，使被选解在目标空间的分布均匀，此时子问题pt对候选解xi的偏好值

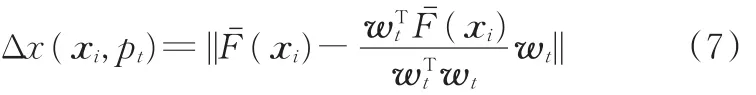
其中，||·||为欧氏距离，Fˉ(xi)是将 F(xi)归一化处理后的目标函数值，其第l个目标函数值为l=1,2,…,m。

2.5.7继续控温回潮后继续升温，温高到影响天麻外观质量枯燥，温度控制在40～50摄氏度至干品，约5天。

对于2N个候选解，可以得到候选解对子问题的偏好矩阵ψx，其维数为2N×N；同理，可以获得N个子问题对候选解的偏好矩阵ψP，其维数为N×2N。

2.1.2 选择具有稳定配对关系的候选解子集

对于N个子问题，如果存在一组配对关系{(p1,x1

),(p2,x2),…,(pn,xn)}(xt∈X)且满足下列关系，则称这N个子问题及其配对的候选解构成稳定配对关系:

最小化总成本定义如下：

从候选解集合X={x1,x2,…,x2N}中选择与子问题构成稳定配对关系的候选解子集合{x1,x2,…,xN}，在保证进化算法收敛性的同时，可以保证选择的解在目标空间具有较好的分布特性，具体配对过程可由文献［12］开发的递延接受程序获得。

2.2 MOEA/D-LSTM算法

候选解xi对子问题pt的偏好值

其中，θ是向量F(xi)-z*与权向量wt的空间夹角。L为设置的控制参数，L越小，限制作用越强。图1b所示为加入限制算子后的稳定配对关系，可以看出，加入限制算子后，被选择到的解分布性能更为优秀。

如果父母禁止儿童自己去探索事物，他们就失去了获得对自然和事物感性经验的途径，其好奇心也会失去成长的土壤。所以父母不能禁止儿童的探索行为，应主动为儿童创造各种良好的环境，借此开拓他们的视野，增强儿童在探索过程中的适应能力，保护儿童探索的自主性、想象能力和创造能力，同时激发培养他们的好奇心。

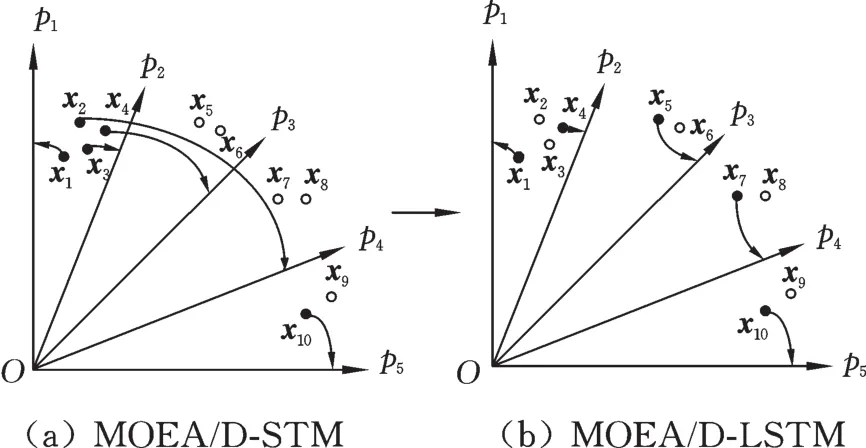
图1 稳定配对关系示例Fig.1 Illustrative examples of stable matching relationships

2.3 利用MOEA/D”LSTM求解FJSP的算法流程

当利用MOEA/D⁃LSTM求解FJSP时，主要包括下列操作：①将原始解空间中可行解进行染色体编码和解码；②对父代染色体进行交叉、变异操作，获得子代染色体；③对染色体进行选择，若满足截止条件，则停止算法，否则重复进行操作②。

Eliminating φ, derivating Equation(7) to t, then subtituting into Equation(6) to obtain the point C line velocity in the XOY system about EDC slider crank mechanism as follows

2.3.1 染色体编码与解码

染色体编码方式为双层编码［13］，每个染色体表示一个可行解，对应工件的加工顺序及所使用的机器。若待加工的工件总数为m，工件i包含ni（ni＞1）道工序，则染色体是长度为的整数串。前i个基因为染色体的第一层即工序编码，基因的顺序决定工序的调度顺序，基因i为工件Ji的编号，基因i在工序编码中第j次出现代表工件i的第j道工序即Oij。后∑ni个基因为染色体的第二层即机器编码，表示加工每道工序的机器编号，基因p表示所用机器编号即Mp。图2所示为一包含3个工件、3台机器的染色体,工序编码为［1 3 2 1 2 3 1］，代表的加工顺序为［O11，O31，O21，O12，O22，O32，O13］，其中，a位置的基因 3在工序编码中第2次出现,表示为O32代表工件3的第2道工序；机器编码为［2 1 3 2 2 2 1］，代表加工每道工序所用的机器为［M2，M1，M3，M2，M2，M2，M1］。

图2 染色体编码Fig.2 Chromosome coding

染色体解码时首先根据工序编码确定工件及相应的工序，然后从机器编码中找出对应的加工机器，从对应的时间矩阵中找到对应位置的加工时间，这样便可确定工序的加工机器和所用时间。依次扫描工序编码即可确定所有工序的加工顺序以及加工参数，从而得到一个完整可行的工序调度方案。

2.3.2 交叉与变异

本文对交叉操作过程中产生的非法染色体进行修复，结合图3对交叉操作（包含修复操作）步骤做详细说明：首先，在工序编码随机选择两个位置a、b，在机器编码中有两个对应的位置a′、b′，将两父代染色体a、b和a′、b′之间的部分调换，得到子代1′和子代2′；然后，对比子代1′、子代2′与父代染色体的工序编码部分，可知子代1′多了一个基因3、少了一个基因2，子代2′多了一个基因2、少了一个基因3，故将子代1′的基因3与子代2′的基因2对调，并对机器编码做相应的调整，得到子代1″和子代2″；由两条染色体工序编码的变化可知，c位置的基因2表示工序O22，c′位置的基因2表示用于加工工序O22的机器2，因此，子代1″工序编码中的两个2都表示工序O21，同理，子代2″工序编码中的两个2都表示工序O21。对子代1″和子代2″进行修复操作：将两条染色体a、b之间的部分（做交换的部分）重新编码，并重新选择加工工序的机器，即调整a′、b′之间的部分；未交换的部分则保持不变。经过交叉操作得到的子代染色体满足约束条件，为可行解。

性状:呈椭圆形或长条形,略扁,皱缩而稍弯曲,长3-15厘米宽1.5-6厘米,厚0.5-2厘米,表面黄白色至黄棕色,有纵皱纹及由潜伏芽排列而成的横环纹多轮,有时可见棕褐色菌索。顶端有红棕色至深棕色鹦嘴状的芽或残留茎基;另端有圆脐形疤痕。质坚硬,不易折断,断面较平坦,黄白色至淡棕色,角质样。气微,味甘。[2]不刮皮天麻外皮皱纹多,习称“姜皮”(又称“蟾蜍皮”);冬麻顶端有红棕色至深棕色鹦嘴状的芽,习称“鹦哥嘴”或“红小辫”;圆脐形疤痕习称“肚脐眼”;断面 角质样,有光泽,习称“宝光”。天麻鉴别口诀“鹦哥嘴,凹肚脐,外有环点干姜皮,松香断面要牢记。

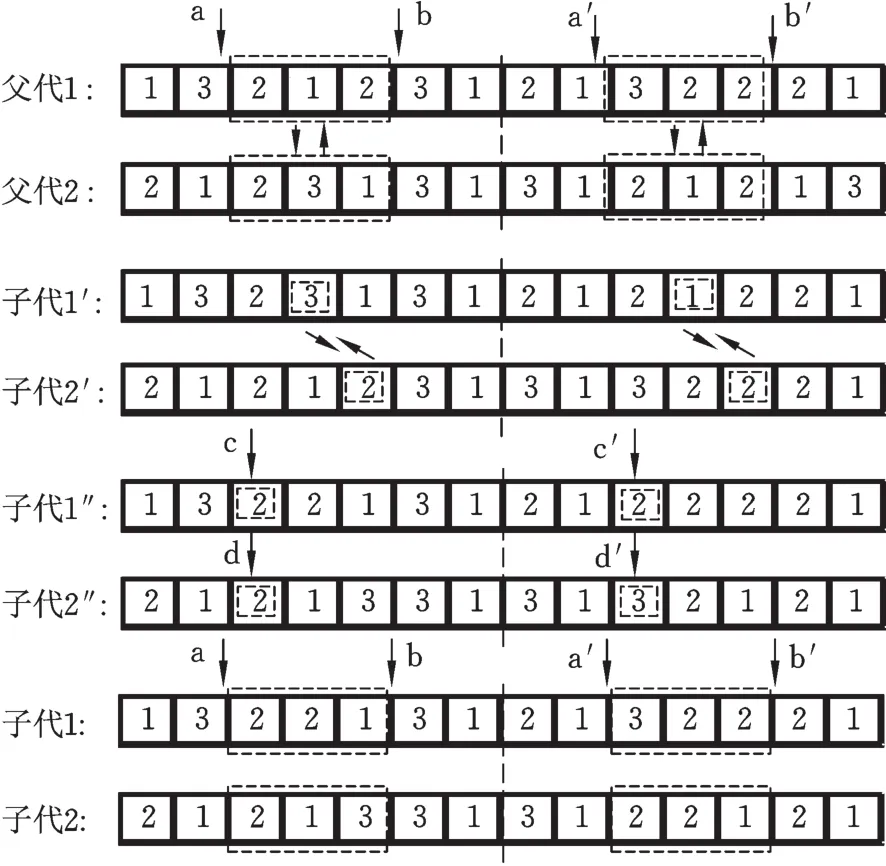
图3 交叉操作示意图Fig.3 Schematic diagram of crossover operator

为了防止算法陷入局部收敛［14］，提高算法的局部优化能力和种群多样性，需要进行变异操作。个体变异过程如图4所示：首先，从经过交叉形成的2个子代染色体中随机选择1个染色体；然后，在工序编码中随机选择基因a、基因b进行交换，此交换将改变工序编码中每个基因所代表的工序，如c位置的基因1在原染色体表示工序O12，在新染色体变为表示O13，d位置的基因2在原染色体表示工序O22，在新染色体变为表示O21，同时机器编码也随之变化。经此变异操作得到的新染色体能够满足约束条件。

图4 变异操作示意图Fig.4 Schematic diagram of mutation operator

2.3.3 染色体选择

本文利用MOEA/D⁃LSTM算法对父代和子代所构成的整个候选集进行选择，以获得具有较高收敛精度和具有广泛分布的目标函数值。

利用MOEA/D⁃LSTM算法求解FJSP的整个算法流程如下。

（1）初始化。①初始化迭代次数K,种群包含染色体个数N,限制算子控制参数L、交叉概率Pc和变异概率Pm；②设置一组均匀分布的权向量w=(w1,w2,…,wN),其中一个向量wt=(wt,1,wt,2,…,wt,m)∈Rm,wt,j≥0,同时可得子问题集合P={p1,p2,…,pN}，计算每一个权向量与其他权向量的欧氏距离，对权向量wt,设置一个集合B(t)={t1,t2,…,tT}，此时 wt1、wt2、…、wtT为离wt最近的T个向量；③随机产生N个整数编码染色体的种群X={x1,x2,…,xN},计算适应度值，令g=1；并初

我虽然以家庭为重，俯首甘为孺子牛，但仍会孜孜不倦地追求自己的所爱：文学与艺术。这只是为了追求过程中所得到的乐趣，并不是为了什么虚名。

（2）更新。①生成N个子代染色体。对于i∈[1，N]，从 B(i)中随机选择两个索引 τ、κ，进而选择两染色体xκ和xτ；将xκ和xτ作为父代染色体进行模拟二进制交叉和变异操作，生成一个子代染色体xN+i。②更新参考点。将父代染色体和子代染色体合并解集合X={x1,x2,…,x2N}；计算适应度值，由z*l=min{fl(xi)}更新参考点。③更新种群。将染色体集合X和子问题集合P作为输入，生成偏好矩阵ψP和ψS；根据偏好矩阵选择优越的子代染色体作为下一次迭代的父代，并置g← g+1。

2、自身方面。小学是一个比较特殊的成长阶段，一般小学生的心理素质都不够强，自控能力也比强，如果遇到难度较大一点的问题，则可能出现畏惧、逃避、不自信和美元耐心等情况，从而产生自我怀疑的心理。

第一，PPP运营模式。从市场视角进行分析，将企业作为主体形成吸引基金，与现阶段所推行的城镇发展等政策引导进行融合，引进国开行与农发行等政策性基金，构建成为全新城镇化建设基金体系。第二，将区域内具有人文与自然元素的地区作为建设对象，结合规划设计与产业运营商等主体，形成一个产业联盟，与政府有关部门签署相应的合约，在建设与运营以及管理等方面进行特色小镇的建设。

设目标空间为F(x)=[f1(x),f2(x),…,fm(x)]∈Rm，m为目标空间的维数。利用一组权向量w=(w1,w2,…,wN)将目标空间划分为N个子空间，其中 wt=(wt,1,wt,2,…,wt,m)∈Rm,t=代表了一个待求解的子问题，N个子问题记为P={p1,p2,…,pN}，则wt代表了子问题pt的权值向量（图1给出了m=2，N=5时的子问题表示）。设X={x1,x2,…,x2N}为多目标进化问题的2N个候选解集合，则子问题pt对候选解xi（i=1，2，…，2N）的偏好值

3 实验设计与结果分析

3.1 仿真算例

3.1.1 实验设置

本文选用CIMS领域经典MK1～MK15算例［15］。将NSGA-Ⅱ、MOEA/D-STM和MOEA/D-LSTM在标准算例上独立运行20次，验证各算法在解决双目标问题的性能。NSGA⁃Ⅱ因其快速排序、及时估算拥挤距离以及容易比较拥挤距离这三个特点，成为CIMS领域最常用的多目标算法之一。NSGA⁃Ⅱ需要设置的参数见文献［16］，MOEA⁃STM需要设置的参数见文献［11］。MOEA⁃LSTM参数设置：种群染色体数目N=40，迭代次数K=400，交叉概率Pc=0.8，变异概率Pm=0.6，限制算子控制参数设置L=2，邻域大小T=10。

3.1.2 算法收敛性能及分布性能分析

算法的收敛性能决定能否得到一个优秀的解决方案，良好的分布性能则是提供给抉择者宽泛选择的保证。为了验证算法的性能，本文以这两种性能指标来考察三种算法。

囊性淋巴管瘤的病理学主要显示为明显扩张的少数淋巴管形成，以类圆形或圆形的囊性病灶为主，边界比较清楚且囊壁菲薄，囊内存在淋巴液，乳糜液占少数。CT的表现主要为具有均匀密度的囊性肿块，边缘比较清楚，囊壁比较薄，多囊者清晰可见分隔，囊内CT值接近水，增强扫描后清晰可见囊壁、纤维分隔轻度强化现象。临近组织出现被包绕或受压移位的情况，但浸润并不明显。位于盆、腹腔内者常可发展巨大，本组1例直径达15cm。

海外中资建筑企业的高质量发展还应体现在产品服务质量的提高以及品牌影响力的提升。“中国制造”在国际上广为人知，但中国制造在很大层面上并没有给消费者带来高质量的信任感。海外中资建筑企业在承接国际工程时无疑具有一定的代表性，既代表国家形象。这种代表性对我国的国际地位与贸易发展，以及全世界对中国制造认识的改观起到至关重要的影响。海外中资建筑企业应不断提高产品和服务质量，精益求精，加强服务监管和环境保护，合规运营，不断提升品牌知名度和影响力，进而提升和改观中国制造的影响力。

表1给出了三种算法获得的最大完工时间和总成本。由表1可以看出，对两目标来说，MOEA/D⁃LSTM在算例MK01、MK02等11个标准算例上找到最优解，而NSGA⁃Ⅱ仅在MK03、MK11上找到最优解，MOEA/D⁃STM仅在MK06、MK09上找到最优解。由此可验证MOEA/D⁃LSTM总体上展现出优于MOEA/D⁃STM和NSGA⁃Ⅱ算法的收敛性能。

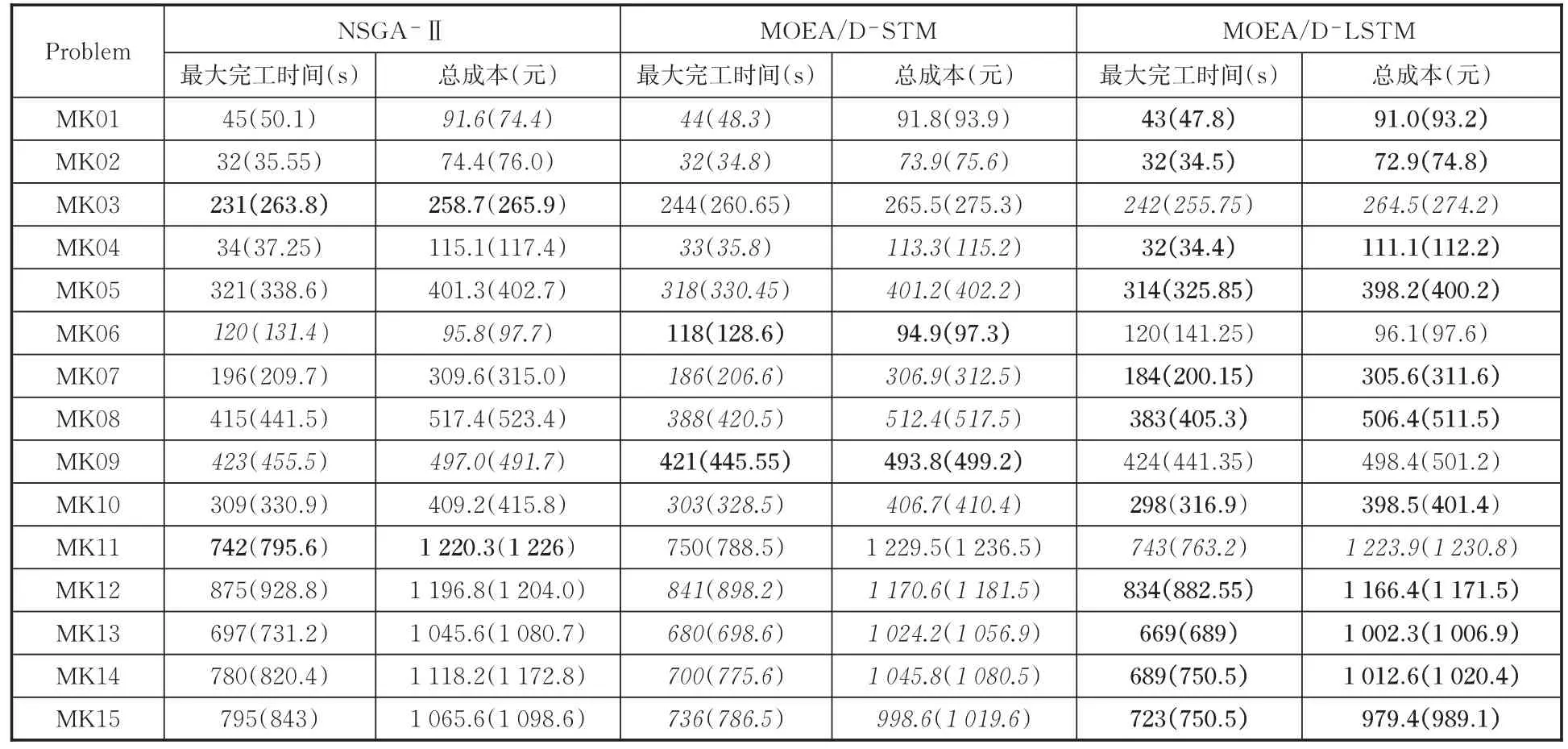
表1 最大完工时间和总成本Tab.1 Maximum completion time and total cost

由收敛性能比较结果可知，MOEA/D⁃LSTM仅在4个标准算例上略逊于其他两种算法。为了不失一般性，在比较算法的分布性能时，本文从15个标准算例中选择MK03、MK11、MK15三个标准算例。对每个算法选择包含最小完工时间染色体的种群，并通过非支配排序得到每个种群的Pareto最优解。由于种群不同，Pareto最优解的个数也会不同。由图5a～图5c可知，NSGA⁃Ⅱ有3个Pare⁃to最优解，MOEA/D⁃STM有7个Pareto最优解，而MOEA/D⁃LSTM则有9个Pareto最优解且在目标空间中分布均匀，分布性能优于前两种算法；由图5e、图5f可看出，NSGA⁃Ⅱ有7个Pareto最优解，但其中3个解拥挤在空间Ω1={(f1,f2)|750≤f1≤800,1230≤f2≤1240}，却没有一个Pareto最优解处于空间Ω2={(f1,f2)|750≤ f1≤ 8001240≤f2≤1250}中；MOEA/D⁃STM有8个Pareto最优解，但其中4个解拥挤在空间 Ω3={(f1,f2)|750≤f1≤800}，2个解拥挤在 空 间 Ω4=(f1,f2)|810≤f1≤830,1230≤f2≤1232},MOEA/D-LSTM在算例MK11上虽然收敛性能不如NSGA-Ⅱ,但是有8个Pareto最优解且在目标空间上均匀分布，分布性能优于前两种算法；由图5g～图5i可以明显看出，MOEA/D⁃LSTM在算例MK15上，收敛性能和分布性能均优于另外两种算法。综上所述，MOEA/D⁃LSTM在标准算例MK01～MK15上的综合性能优于另外两种算法。

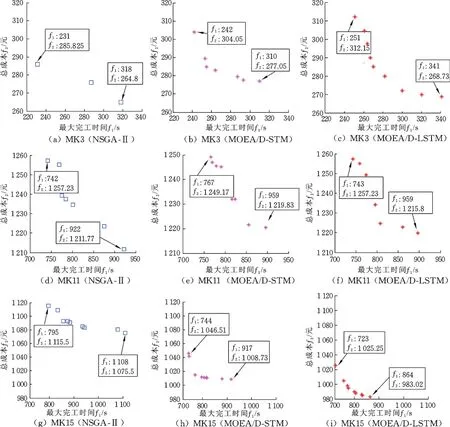
图5 3种算法的分布性能比较Fig.5 Distribution comparison of three algorithms

3.2 实例验证

本文以某制桶公司第一生产车间10月份某一订单为例，验证MOEA/D⁃LSTM解决双目标FJSP的性能。订单包括6×30个桶，从原材料到成品需要经过10道工序，该生产车间共有28台机器（编号1～28）用于加工。车间设备名称与编号列于表2，6种桶所需加工工序及其可用的加工机械、所用加工时间如表3所示。

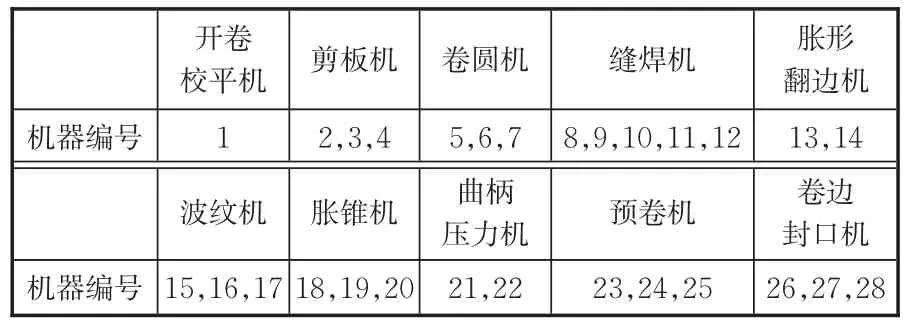
表2 设备及编号Tab.2 Equipment and number

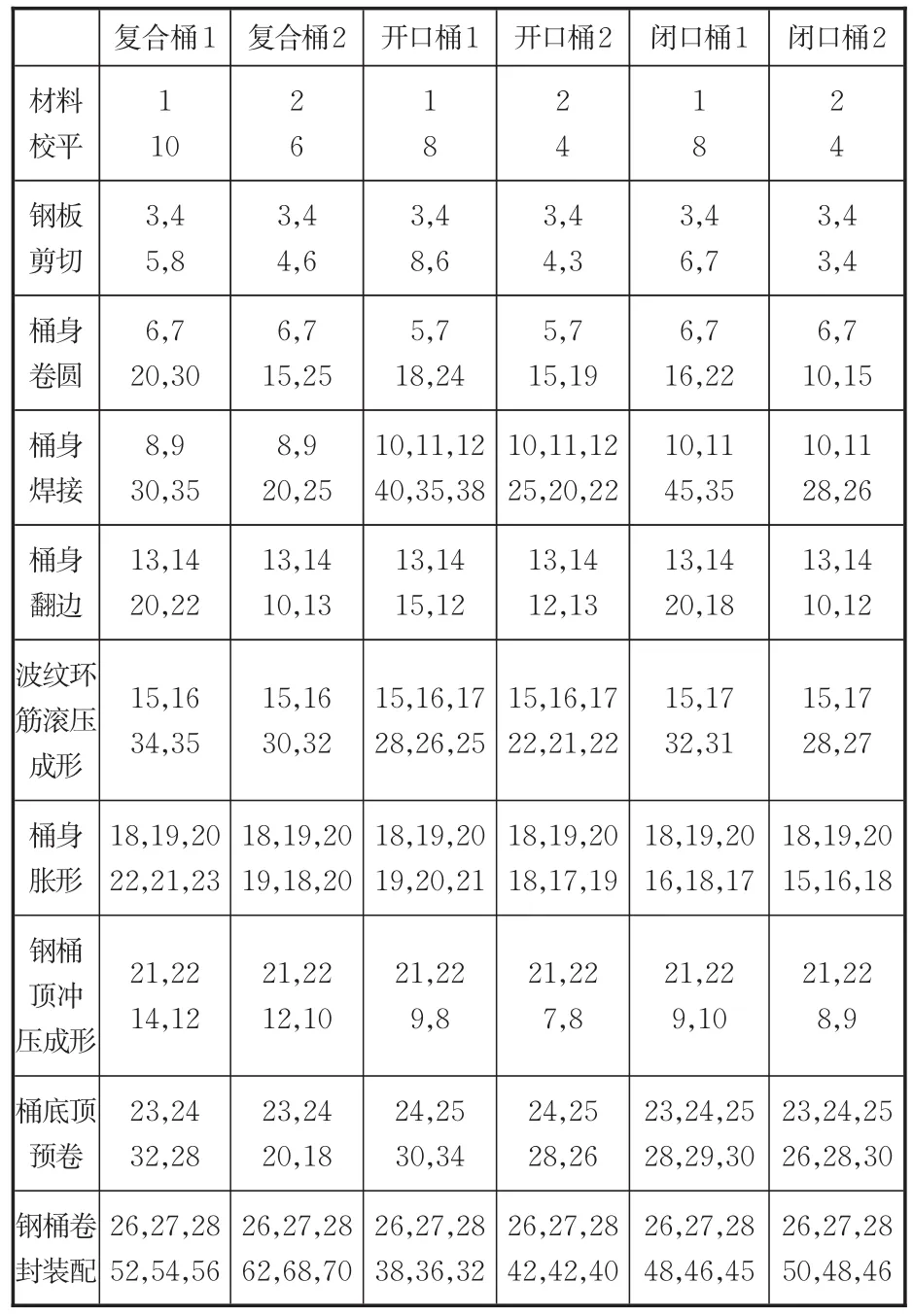
表3 工序与加工设备Tab.3 Processes and processing equipment

使用3种算法处理该订单，不考虑工件在机器间转移的时间，实验各参数不变，所得结果如表4所示。由表4可知，MOEA/D⁃LSTM算法所得到的最大完工时间最优解为3 991 s，加工成本最优解为5 010.4元，比其他两种算法得到的最优解更好。分布性能如图6所示，由图可知，MOEA/DLSTM算法提供了更为宽泛的调度方案。

2007年9月20日，选择相对理想的运行条件下对泵站发电效率进行了测试，发电水头为6.24 m，以沙集站#4和#5机组发电数据测试为例，机组效率计算公式为：

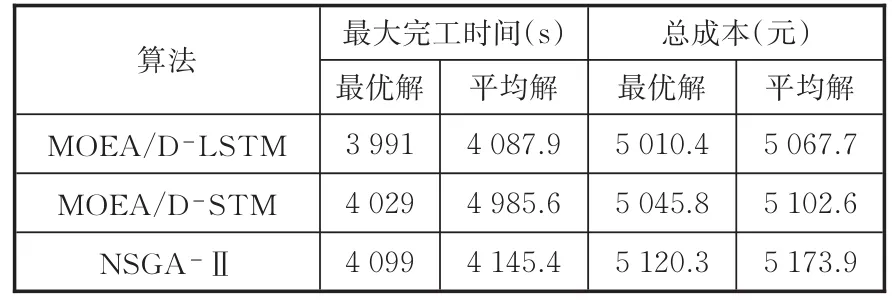
表4 实例仿真结果Tab.4 Example simulation results

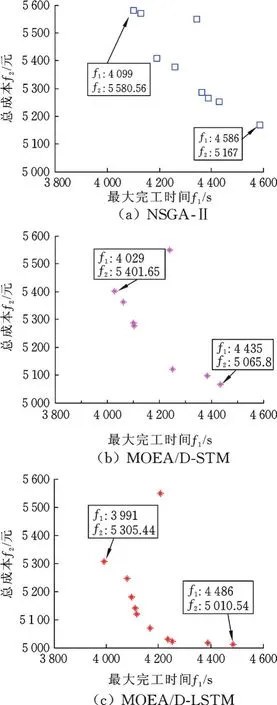
图6 3种算法的分布性能比较Fig.6 Distribution comparison of three algorithms

4 结论

针对MOEA/D⁃STM以及常用算法求解FJSP过程中的弊端，本文提出一种带有限制算子的进化算法MOEA/D⁃LSTM。该算法利用了染色体在目标空间中的位置信息，将位置信息和限制算子相结合计算一个新的偏好值，从而得到一个带限制算子的偏好列表。在配对过程中可以使子问题选择更适合的解，以使每一代解均匀分布，最终得到更好的最优解以及更好的分布性能。从对15个双目标标准测试集和实例的实验结果看，MOEA/D⁃LSTM在保持MOEA/D⁃STM的优良性能的基础上，进一步提高了收敛性能，同时解决了原算法出现的解分布不均匀的问题，给决策者提供更为宽泛的调度方案。

本文未考虑原材料的价格变化、库存量及成品存储费用对最终优化结果的影响，下一步的研究内容将会把原材料的价格波动、原材料库存量以及成品存储费用考虑在内，进一步模拟现实情况。