深海张力腿平台非线性涡激振动响应特性分析

孙友刚 董达善 强海燕 王 冉

1.上海海事大学物流工程学院，上海，201306 2.同济大学机械与能源工程学院，上海，201804

0 引言

张力腿平台（tension leg platform，TLP）是进行深海油气开发的重要工具，其升沉运动小，适用水深大［1⁃3］。但是，张力腿长度的增大使自振频率降低，由于深海流速较大，海流激发比基频弯曲模态更高的弯曲模态，增大了发生涡激共振的流速范围；而且，海流的幅值和方向沿张力腿长度方向是变化的，这可能会激起多阶模态的涡激振动；就结构自身而言，张力腿长度增大，其自身非线性效应也会随之增大，就必须考虑自身结构非线性因素的影响；另外还存在低频慢漂运动、二阶和频力和高阶脉冲力共振等问题。由此可知，深海平台张力腿涡激振动问题要比浅水、固定式平台更复杂，张力腿在深海中的非线性动态特性需要进一步研究。

波浪海流共同作用产生的涡激振动容易引起张力腿的疲劳破坏。许多学者对涡激振动的发生原因、锁频共振现象、流体动力学计算以及动态响应等问题展开了研究。GADAGI等［4］求解计算平台在不同预张力下的动力响应，分析了不同有效波高下张力腿的响应以及系缆的应力。CHEN等［5］研究了波浪作用下Mini张力腿平台的耦合响应特性。董艳秋［6］将张力腿简化为欧拉梁，采用多项Galerkin法计算了当结构固有频率与涡激频率接近时，张力腿的单自由度涡激振动响应。谷家扬等［7］考虑波流联合作用，求解张力腿的涡激非线性动力响应。HAN等［8］采用非线性刚性梁和柔性梁模型，计算结构的动力响应，但在模型中忽略了平台的运动。KUCHNICKI等［9］推导了张力腿受到涡脱落载荷作用的振动方程，但在模型中没有考虑平台的运动。徐万海等［10］应用二维非线性梁模型计算结构动力响应，结果表明张力腿轴向与流向有很明显的耦合效应，但在模型中忽略了扭转效应与转动惯量的影响。麦继婷等［11］将张力腿简化成欧拉-伯努利梁，建立了张力腿的横向振动方程。瞿元等［12］把平台张力腿简化为平面柔性梁，比较了在横向有限应变存在下不同涡激载荷幅值下的运动响应，但在模型中忽略了平台的运动和流体阻尼力作用。综上所述，在海洋平台非线性动态特性方面已经取得了重要进展，但还存在一些不足，如对于影响平台张力腿非线性参激耦合运动的许多因素，考虑还不够全面；对于非线性耦合运动特性及引起大幅运动的原因，还缺乏本质的和规律性的认识等。

基于上述原因，本文在深海平台张力腿动力学分析时，不仅考虑平台作用力、波浪、海流、动张力等复杂载荷的联合作用，还充分反映结构自身非线性因素的影响，建立了深海平台张力腿非线性多自由度耦合运动方程。

1 空间非线性动力学模型

1.1 空间模型与假设

将张力腿考虑为空心的柔性空间梁结构，两端采用铰支，其中底端为固定铰支座，顶端为移动铰支座，平台空间运动对张力腿的作用采用顶端的位移边界条件来施加。张力腿的空间模型见图1。

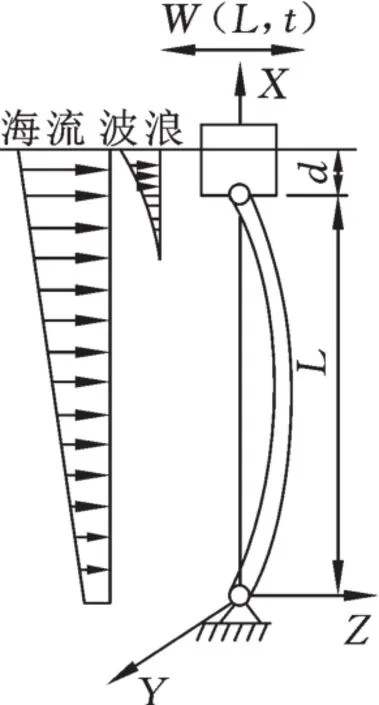
图1 张力腿空间模型Fig.1 3D model of tension leg

假设条件：①梁在线弹性范围内工作，忽略其横向应变；②梁在弯曲过程中，横截面始终与中性面垂直；③忽略梁绕自身轴线的扭转效应和温度所引起的应变；④海流和波浪沿着同一方向传播，海流的速度随着水深变化。

如图2所示，考虑空间梁的原始长度为L，轴向位移为u(X,t)，横向位移为v(X,t)，流向位移为w(X,t)，虚线表示初始形状，实线表示变形后形状。

图2 空间梁中心面的初始形状和变形后形状Fig.2 The initial and deformed shape of the center plane of 3D beam

1.2 应力、位移和应变

根据Kirchhoff假设，柔性梁的3个方向的位移可表示为

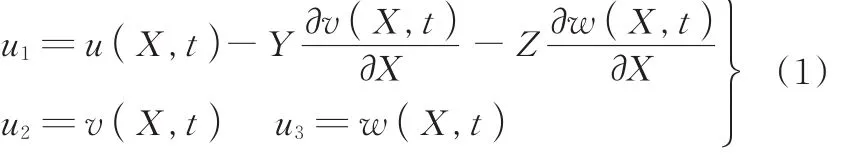
式中，u1、u2、u3分别为X、Y、Z方向的位移；u(X,t)为中性面轴向（X向）位移；v(X,t)为中性面横向（Y向)位移；w(X,t)为中性面流向（Z向）位移。

假设梁的应变是小应变，并且可以适度旋转，可得

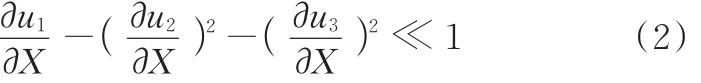
将式（1）、式（2）代入格林应变公式得

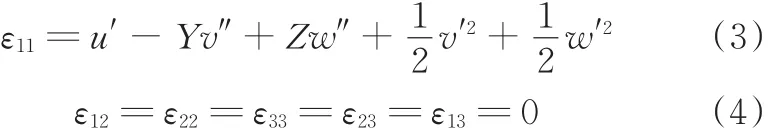
式中，εij为应变。

本文中，(')表示∂∂X；（·）表示∂/∂t。

1.3 Euler⁃Lagrange方程

结构的应变能

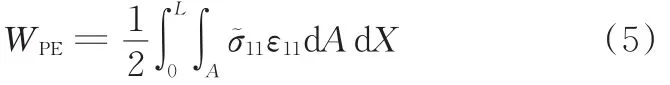
式中，A为梁的横截面面积；σ~ij为所受应力。

应变和应力的本构方程：

根据假设②，变形后横截面的平面仍与变形后的轴线相垂直，这就导致了泊松比并不会影响到结果［13］。不考虑泊松比，可得

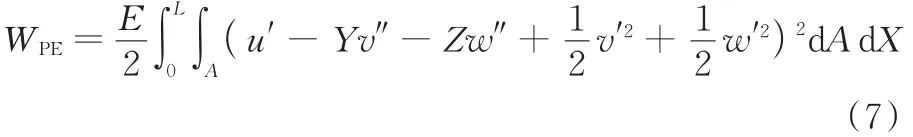
由于在积分时，Y、Z的奇次项积分为零，Y2、Z2的积分分别是对Z轴和Y轴的截面惯性矩，即

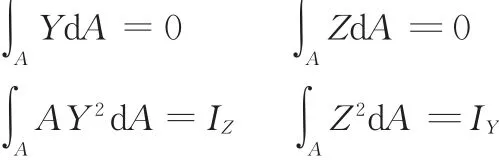
式中，IZ为张力腿横截面对Z轴的惯性距；IY为张力腿横截面对Y轴的惯性距。

则式（7）可简化为

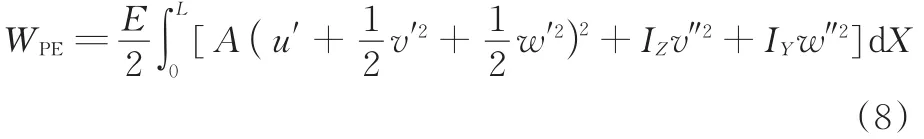
结构的动能：

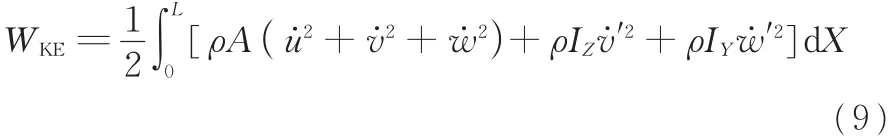
则Lagrange函数为

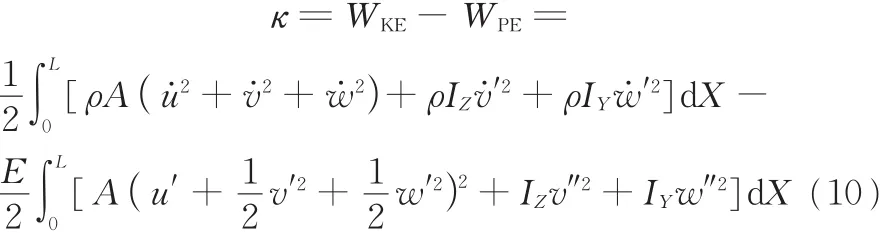
综合以上，我们就得到了结构的动能、势能（应变能）和相应的Lagrange函数。

1.4 空间动力学方程的推导和边界条件

依据Hamilton原理，有

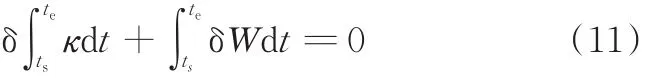
式中，ts、te分别为起始和结束时间点；κ为拉格朗日函数；δW为外力所做的虚功。

δW的表达式：

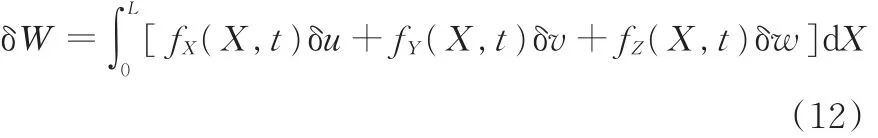
式中，fX(X,t)、fY(X,t)、fZ(X,t)分别为结构在X、Y、Z方向所受的均布载荷。

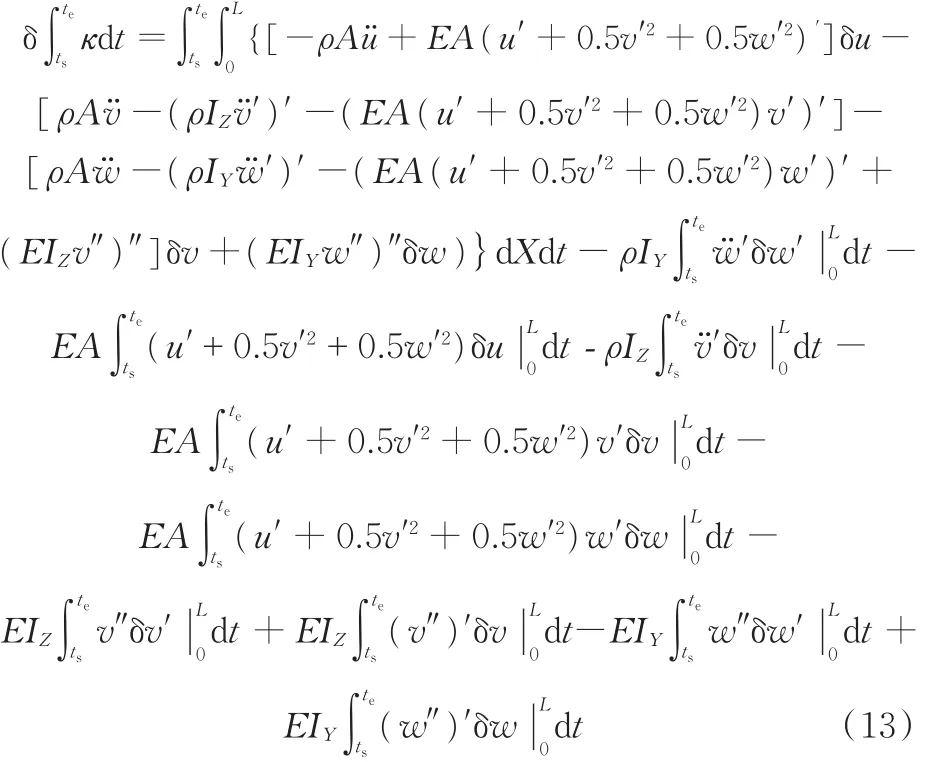
式中，ρ为结构的密度；A为张力腿横截面面积；E为结构材料的弹性模量。

根据Hamilton原理式（11），得空间动力学方程：

式中，fX为结构轴向载荷；fY为结构横向载荷；fZ为结构流向载荷。

TLP在风、浪和流的作用下会发生复杂的运动。若将平台看成是一刚体，则其运动有6个自由度，分别为纵荡、横荡、垂荡、横摇、纵摇和艏摇，并且平台的运动及其所在位置对张力腿的设计有重要影响。在计算张力腿的响应时，通常把平台运动响应施加到张力腿的控制方程的边界条件上。TLP底端为固定铰支座，顶端为移动铰支座，限制了平台的转动和横荡，我们考虑平台纵荡和垂荡运动［14⁃15］。

相应的边界条件如下：

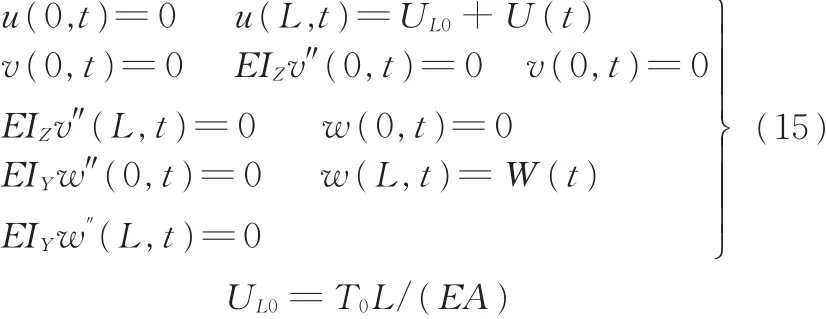
式中，UL0为在初始预张力作用下，顶端所产生的初始位移；T0为张力腿的初始预张力；U(t)为张力腿平台垂荡运动形式；W(t)为张力腿平台纵荡运动形式。

2 结构载荷

2.1 轴向载荷

对于结构的轴向作用力，我们只考虑结构的自重和浮力，可近似表达为

式中，ρf、ρ分别为海水和结构物密度；Vf、V分别为海水和结构物体积。

2.2 横向载荷

结构的横向作用力由两部分组成，一部分是漩涡脱落过程产生的涡激升力，记为FL(X,t)；另一部分是横向运动产生的流体的阻尼力，记为FD(X,t)，则

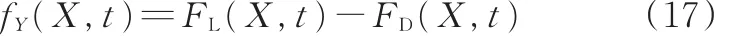
涡激升力可近似表达为漩涡泄放频率的简谐函数，当泄放频率与结构的固有频率相近时，结构就会发生谐振。涡激升力：

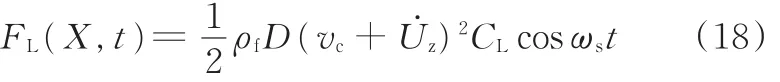
式中，D为张力腿的直径；vc为海流速度；U˙z为波浪水质点水平速度；CL为升力系数；ωs为涡激频率。

水平波速分别采用规则波和随机波两种，流速沿水深变化。

（1）线性波。线性波的波面方程和波速为

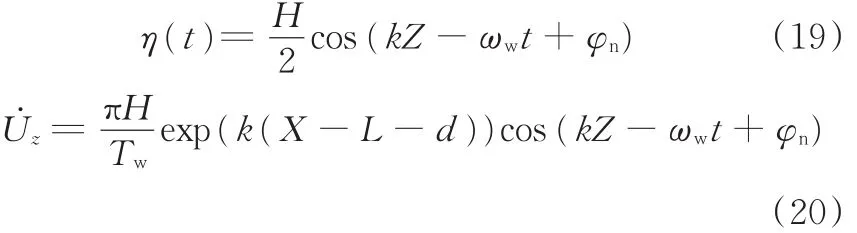
式中，H为波浪高度；Tw为波浪周期；k为波数，k=2π Lw,Lw为波长；d为平台吃水深度；ωw为波浪频率；φn为相位角。

（2）随机波。本文采用Pierson⁃Moskowitz海浪谱（P⁃M谱）表述随机波，其基本形式为

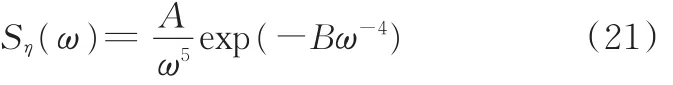
功率谱可以用有效波高Hs表示，Hs可以定义为

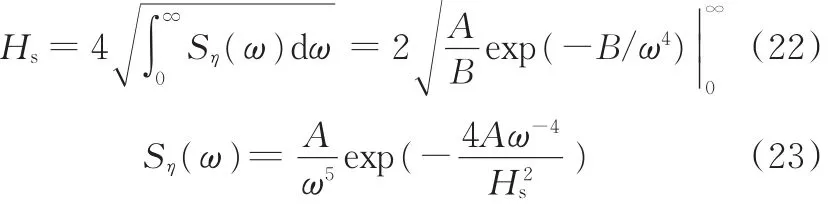
随机波的波面方程可以看作无数个振幅不同、波频不同、初相位随机的简谐波累积叠加而成，但在实验分析中一般可以选用有限个简谐波模拟，即

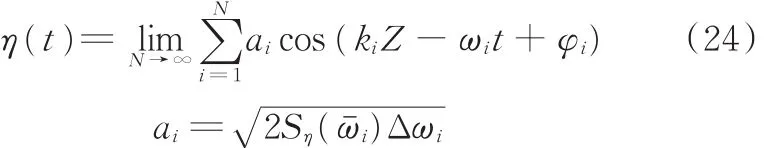
式中，ai为第i个波的波高；ωi为第i个波的频率。基于Ariy波理论可以得到随机波的水平波速为

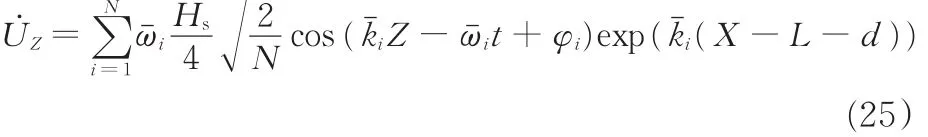
随机波的水平加速度为

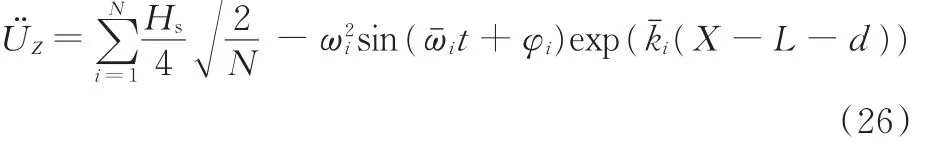
假设海流沿水深线性变化，其流速为

式中，X为垂直方向位移。

结构横向运动产生的流体的阻尼力，采用莫里森（Morison）公式描述：

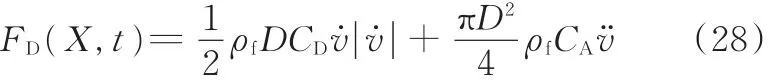
式中，CD为黏性阻力系数；CA为附加质量系数。

所以，结构的横向作用力为

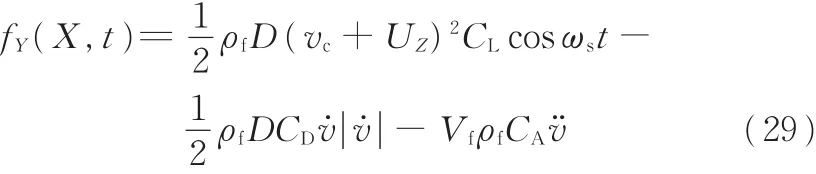
2.3 顺流向载荷

由于圆柱尾流涡街的形成，对于结构的顺流向作用力可以分为两部分：尾流涡街引起沿流向的脉动拖拽力和波浪的作用力。这样顺流向受力可以表达成：

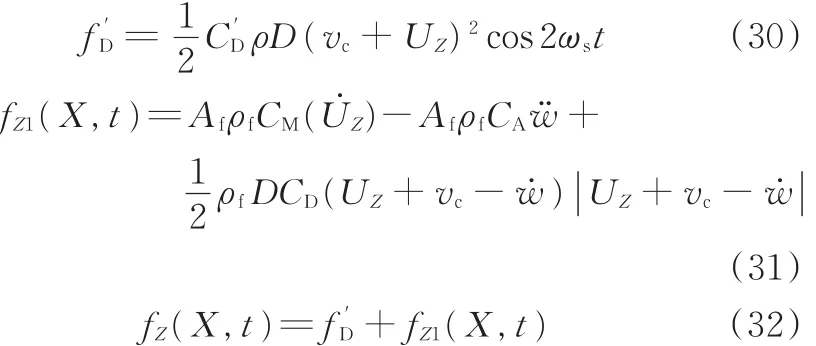
式中，CM为惯性力系数为脉动拖拽力系数。

3 数值计算与分析

3.1 定常流线性波结构动力响应

对于采用线性波、线性流的动力学方程，可以用伽辽金法对方程进行变量分离求解。空间模态方程的求解采用经典四阶龙格库塔方法。张力腿计算参数的选取见表1。

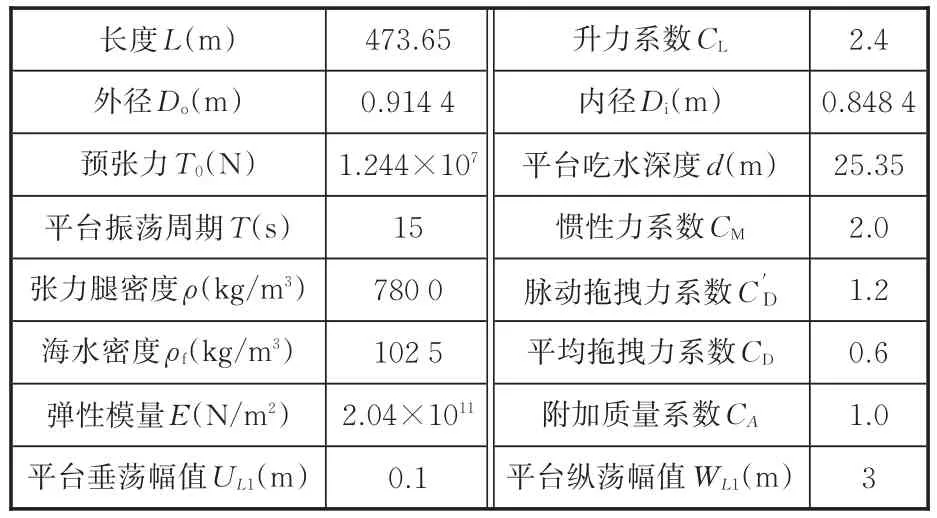
表1 张力腿参数Tab.1 Parameters of TLP

3.1.1 流速对结构响应的影响

海流流速对振动响应的影响比较复杂，流速增大使激励力幅值增大，导致响应幅值增大，但流速增大又会使流体的阻尼力增大，导致响应幅值减小。

为了观察海流流速对结构动力响应的影响，结构参数参照表1，其波浪参数见表2。当流体流经结构时，雷诺数Re对漩涡的形成和泄放产生影响。漩涡的泄放频率fs称为斯托罗哈尔（Strouhal）频率，可依据下式确定：

式中，D为柱体直径；S为Strouhal数，是个无因次数，与雷诺数Re相关。

表2 波浪参数表1Tab.2 Parameter table 1 of wave

当Re＜47时，尾部无涡流形成，Re＞400时，有涡流形成，且S≈0.20±0.02。这里取S=0.20。

图3是流速分别为0.2 m/s、0.6 m/s、1.4 m/s、2.2 m/s下张力腿沿轴线中点处的横向位移时程曲线图。可以发现除了图3a，其余横向位移振动形式基本一致，并且随着流速的增大，其位移振动频率越来越快。图4是海流流速在0.05～2.5 m/s变化过程中横向位移振幅的变化。随着海流流速的增大，横向位移幅值也逐渐增大，并且发现在当流速为0.45 m/s时，其幅值最大，主要是由于结构的漩涡脱落频率接近结构的固有频率，发生共振，此时的漩涡脱落频率为0.618 rad/s。

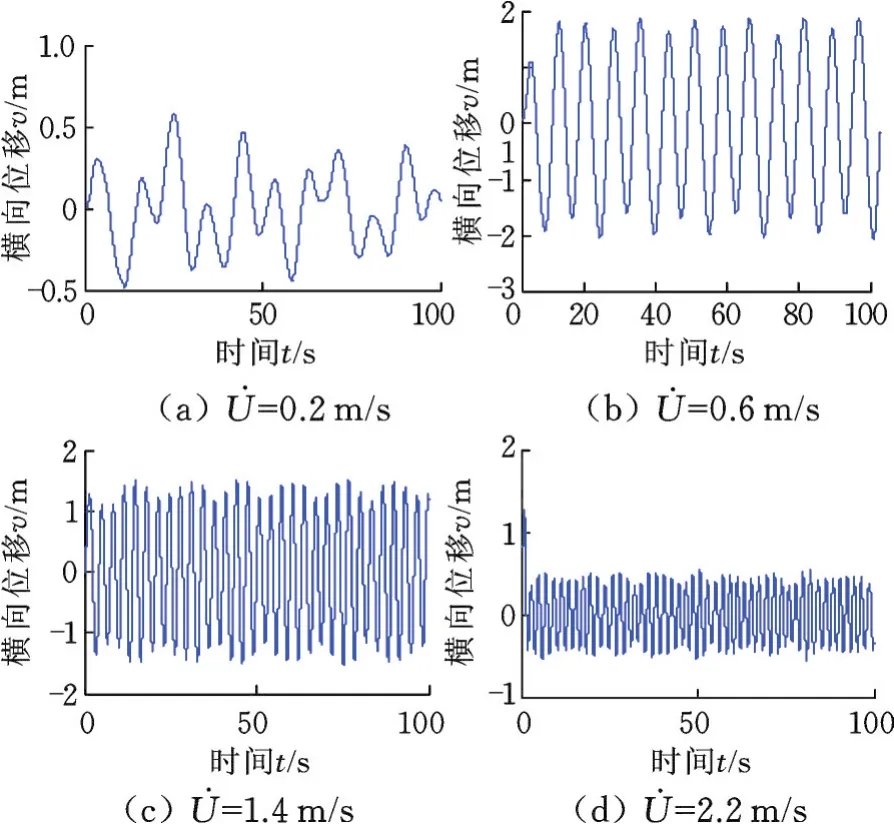
图3 不同海流流速下张力腿中点处的横向位移Fig.3 Transverse displacement in the middle of the leg under different current velocity

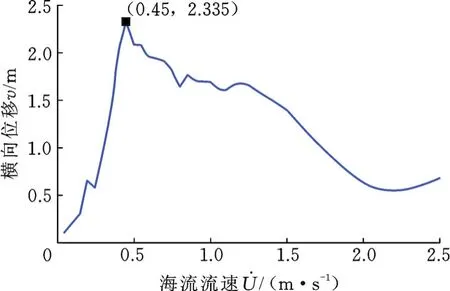
图4海流流速对横向位移振幅的影响Fig.4 Effect of current velocity on transverse displacement

图5 是流速分别为0.2 m/s、0.4 m/s、0.8 m/s、1.2 m/s下张力腿中点处的顺流向的位移时程曲线图。可以看出海流流速发生变化，但其位移的振动频率几乎不变；随着海流流速的增大，其位移曲线整体上移。随着流速增大，考虑和未考虑脉动拖拽力的两条曲线的位移差值也随之增大。

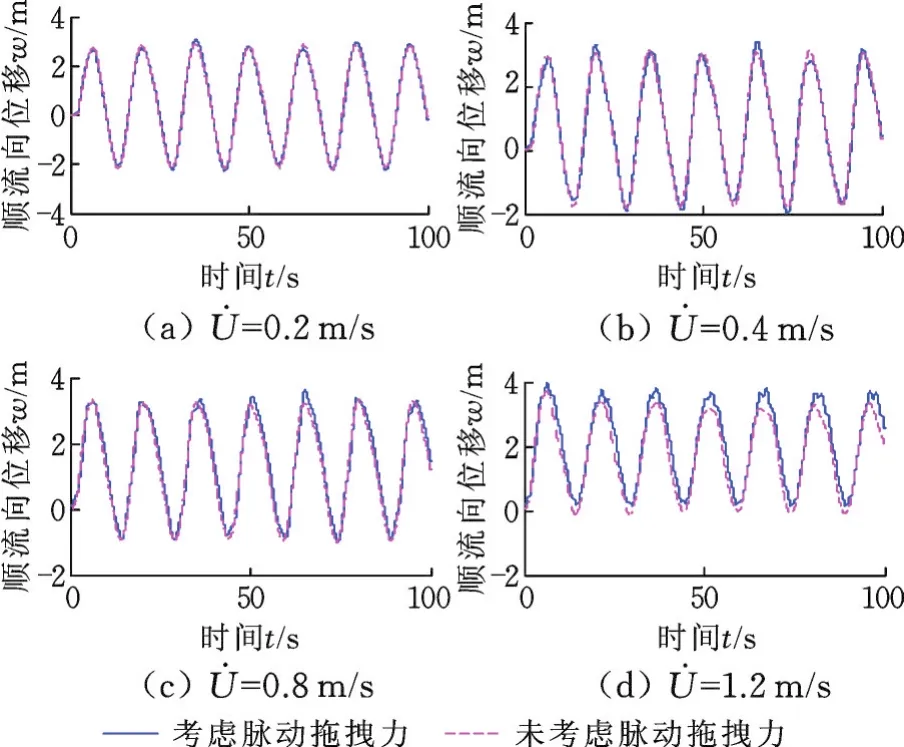
图5 不同海流流速下张力腿中点处顺流向位移Fig.5 In line displacement in the middle of the leg under different current velocity

3.1.2 波高对结构响应的影响

这里主要考虑结构受波浪的单独作用，选取表3的参数，计算张力腿的结构动力响应。

波频 ωw（rad/s）0.593 8涡激频率ωs（rad/s）0.62有效波高Hs（m）10，15，20

图6是仅波浪作用下张力腿中点处的横向位移时程图，可以看出，横向位移随着波高的增大而增大；而图7所示波流联合作用时，此时海流流速vc=0.45 m/s，发现波高虽有变化，但其位移曲线都很接近，说明波高对横向位移响应贡献比较小。图8是仅波浪作用下张力腿中点处的顺流向位移时程图，可以看出，且波高对结构顺流向位移的影响很小。

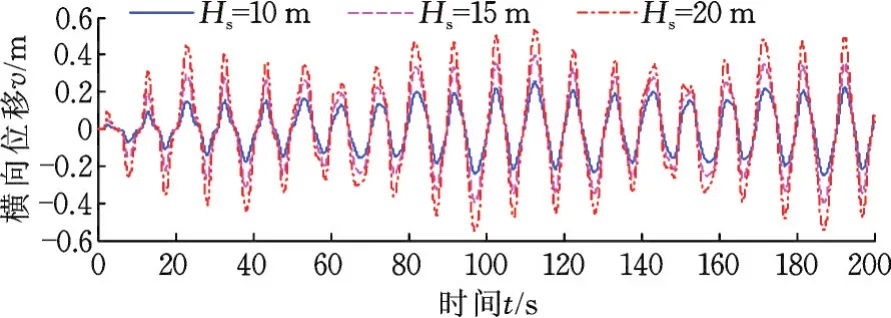
图6 仅波浪作用下张力腿中点处横向位移Fig.6 Transverse displacement in the middle of the leg under wave

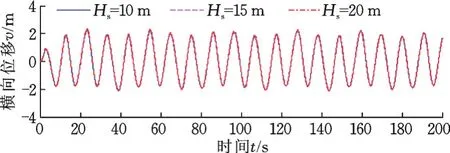
图7 波流联合作用下张力腿中点处横向位移Fig.7 Transverse displacement in the middle of the leg under combined action

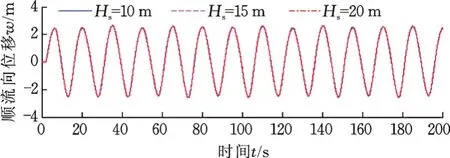
图9 和图10分别是张力腿在不同波高下的横向均方根弯曲应力和顺流向均方根弯曲应力。对于图9，弯曲应力随着波高的增大而增大，在靠近张力腿顶端处其弯曲应力最大。在图9中，波高只对靠近张力腿顶端部分起作用，对结构其余部分几乎没有影响。

3.1.3 波浪圆频率对结构响应的影响

不考虑海流的作用，选取表1和表4的相关参数。图11为不同波频与中点处横向位移的关系。可以看到，其中点处横向位移随着波频的增大而减小，衰减速度很快。

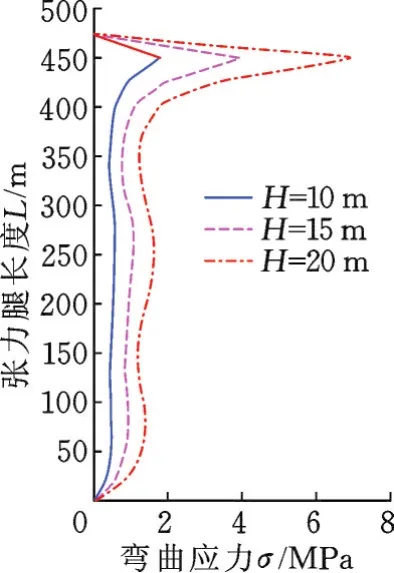
图9 横向均方根弯曲应力Fig.9 Transverse MST bending stress of the leg

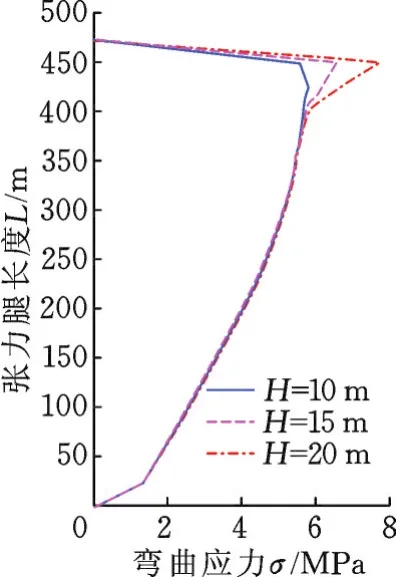
图10 顺流向均方根弯曲应力Fig.10 In line MST bending stress of the leg

表4 波浪参数表3Tab.4 Parameter table 3 of wave

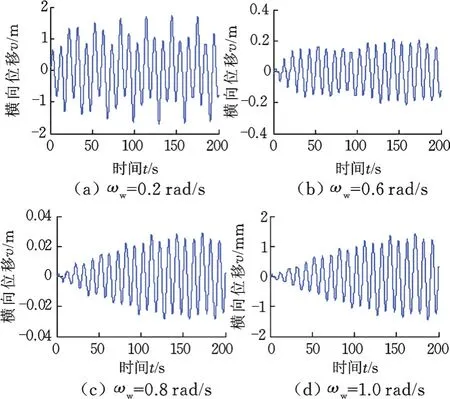
图11 不同波频下张力腿中点处横向位移Fig.11 Transverse displacement in the middle of the leg under different frequency

3.1.4 升力系数对结构响应的影响

选取表1和表5的相关参数，计算升力系数对结构横向响应的影响，如图12所示。

表5 环境参数Tab.5 Parameters of environment

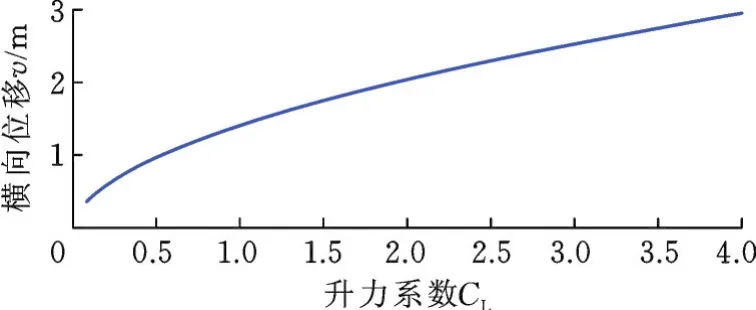
图12 升力系数CL与张力腿中点处最大横向位移的关系Fig.12 Relationship betweenCLand max transverse displacement in the middle of the leg

由图12可见，升力系数在0.01～3变化过程中张力腿中点处横向位移幅值变化，随着升力系数的增大，其横向最大位移也随之增大，并且近似于线性增长。

3.1.5 脉动拖拽力系数对结构响应的影响

选取表1和表5的参数，计算脉动拖拽力系数与张力腿中点处顺流向位移幅值的关系，见图13。

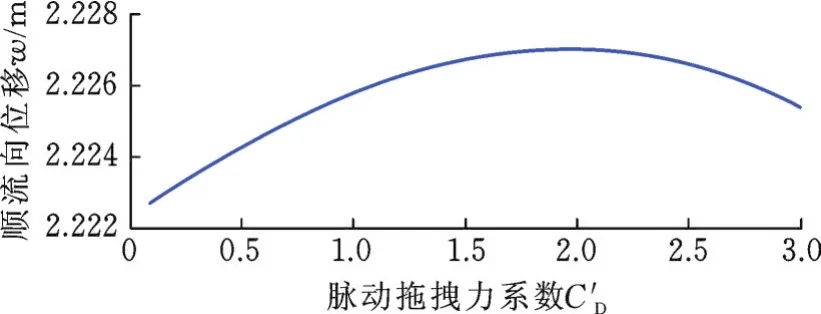
图13 脉动拖拽力系数C′D与顺流向位移的关系Fig.13Relationship betweenC′Dand in line displacement

明显看出：当0＜C′D＜2，顺流向位移幅值呈现近似线性增长趋势；当2＜C′D＜3，幅值又呈现减小趋势，并且两种趋势的位移幅值变化均很小。

3.2 随机波结构动力响应

对于考虑平台运动的梯度流、随机波下的动力学方程，由于用伽辽金法推导其模态方程比较复杂，所以宜采用有限差分法来简化运动方程，再采用四阶龙格库塔方法求解其动力响应。

考虑到我国南海流场的特点，选取南海一座典型的张力腿平台来研究其在南海工况（一年一遇海况和百年一遇海况）下的动力响应。南海平台张力腿的结构参数和环境载荷参数参考文献［16⁃17］。

使用线性叠加法来模拟随机波的波面时间历程。图14和图15分别为不同有效波高的P⁃M谱图和不同波高下的波面时间历程图。

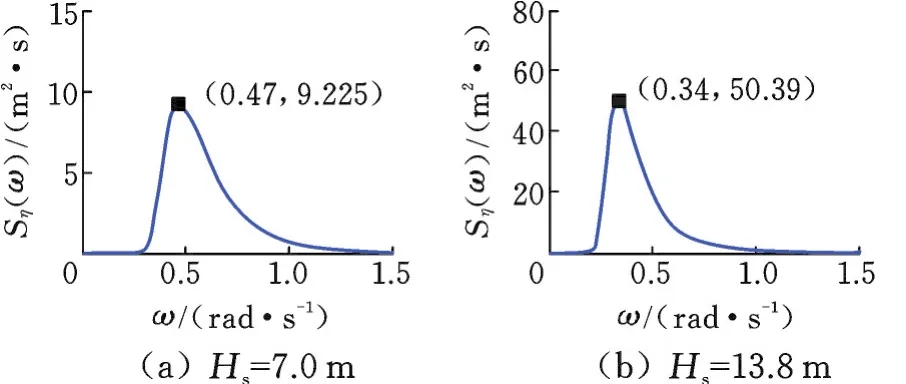
图14 不同有效波高下的P”M频谱Fig.14 P”M spectrum under different significant wave height

由于在真实的海洋环境中，不同水深不同流速会产生多个漩涡脱落频率，结构的振动会变得复杂。为了便于分析结构的动力响应，本节仅考虑漩涡脱落频率等于结构固有频率，即ωs=0.1555rad/s，取一年一遇海况和百年一遇海况进行计算。

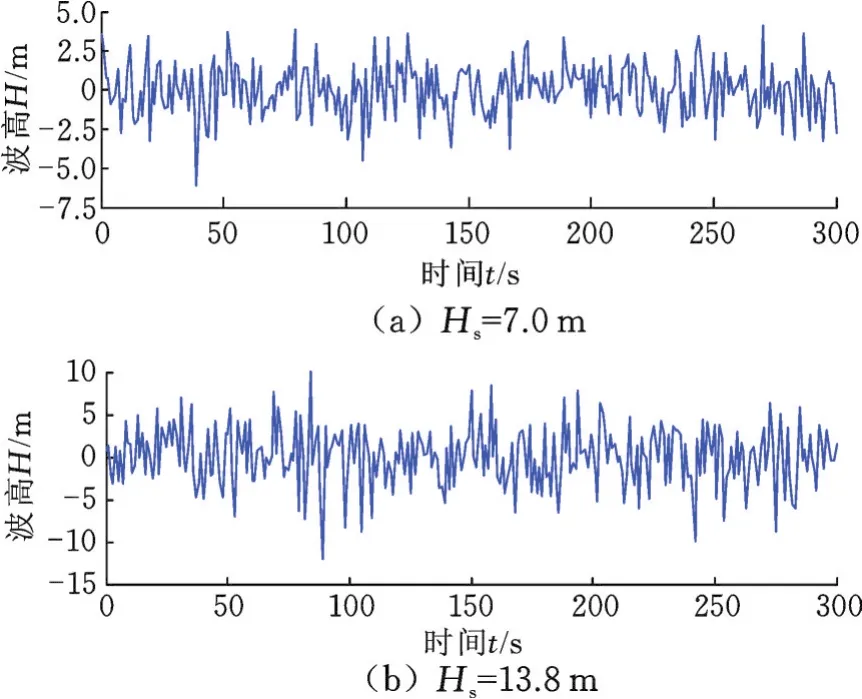
图15 不同有效波高下的波高与时间关系曲线Fig.15 Wave height and time curve under different significant wave height

图16 是一年一遇海况和百年一遇海况下张力腿中点处横向和顺流向时间历程曲线图。图17为上述两种工况下张力腿横向位移和顺流向位移的关系。顺流向振动频率约为横向振动频率的2倍，横向位移变程约为顺流向位移变程的4倍，并且其振动呈现斜8字形状。

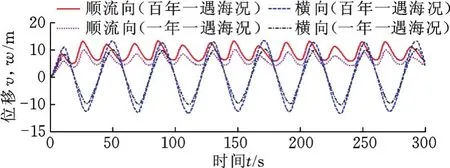
图16 张力腿中点处横向和顺流向位移Fig.16 Transverse displacement and in line displacement in the middle of the leg

图17 张力腿中点处v与w关系Fig.17 Relationship between transverse displacement and in line displacement in the middle of the leg

图18 是一年一遇海况下张力腿的横向和顺流向的弯曲应力均方根图。张力腿应力分布表现为底部和中部的应力较小，而在上部的应力较大；横向和顺流向的弯曲应力最大发生处都在1 403 m，此时横向应力为14.15 MPa，顺流向应力为13.76 MPa。

图19是百年一遇海况下张力腿的均方根弯曲应力图。与图18一样，最大应力发生在张力腿顶端处，其横向最大弯曲应力为37.43 MPa，顺流向最大弯曲应力为25.22 MPa。

图18 一年一海况遇下张力腿均方根弯曲应力图Fig.18 MST bending stress under a once”in”a year sea condition

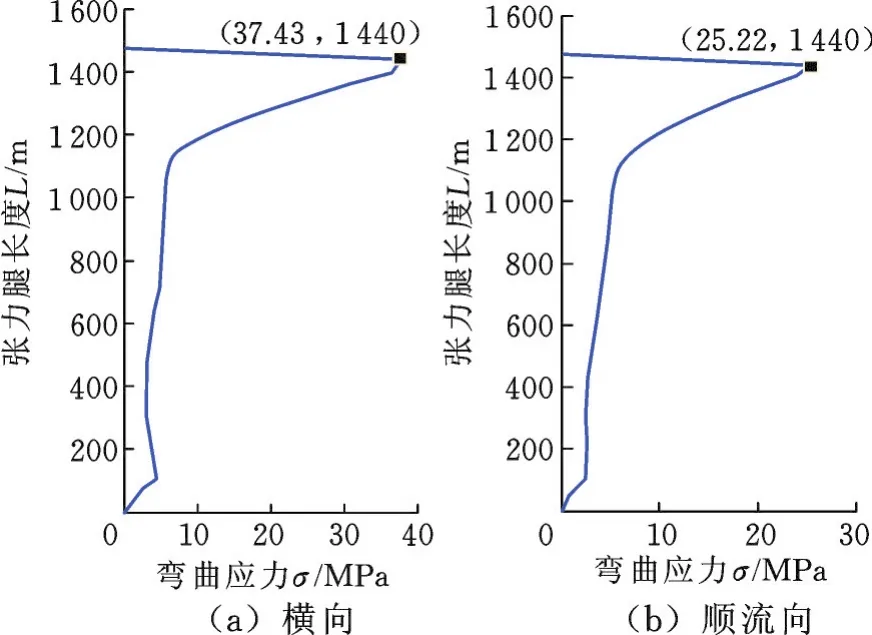
图19 百年一遇海况下张力腿均方根弯曲应力图Fig.19 MST bending stress under a”hundred”year sea condition

4 结论

（1）海流流速对结构横向响应的影响较大，流速越大，振动频率越大。漩涡脱落频率接近固有频率时，激发涡激共振；对结构的顺流向位移也有明显影响，流速越大，其位移时程曲线整体上移越快，同时发现流速越大，其脉动拖拽力对响应就越明显。

（2）考虑波高的变化，发现波高对结构沿轴线方向中点处横向和顺流向位移的影响不明显；但是对顶部弯曲应力的影响显著，波高越大，其弯曲应力越大。

（3）考虑波浪圆频率的变化，发现波浪圆频率越大，结构中点处横向位移越小，而且减小速率很快；对其顺流向位移的影响不明显。

（4）结构横向位移随着横向升力系数增大而增大，呈线性增长；顺流向位移对脉动拖拽力系数的变化不敏感。