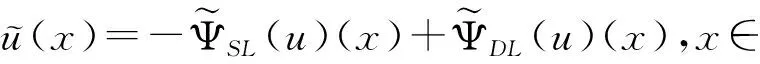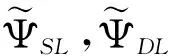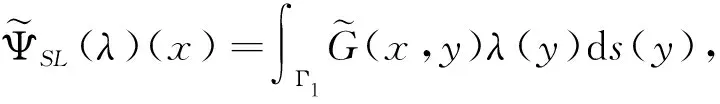时谐散射问题的一种各向异性的优化PML方法
2018-09-21杨孝英
杨 孝 英
(长春工业大学数学与统计学院,吉林 长春 130012)
近年来,很多学者使用PML方法求解散射问题.[1-3]文献[4-7]给出了求解散射问题的一种优化PML方法,文献[8]给出了求解不连续波数的散射问题的各向异性PML方法.由于散射问题的优化PML方法的计算不依赖PML层的厚度,本文主要研究时谐散射问题的各向异性优化PML方法.
考虑如下的二维时谐散射问题:
(1)
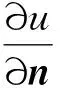
(2)
(3)
其中:r=|x|;f∈(H1(Ω))′的支集在B(R0)={x∈R2||x| (4) (5) 其中:A(x)=J(x)DF-1(x)DF-T(x),J(x)=det(DF(x)),DF(x)为Jacobi矩阵. (6) (7) (8) (9) (10) (11) 图1 各向异性PML层的构造 下面给出如下的复坐标拉伸变换:对于t>0,令 α(t)=η(t)+iσ(t),η(t)=1+ζσ(t) (12) 其中m≥2,ε0>0为足够小的参数. (13) 其中m≥2为常数. 证明由于 (14) (15) 其中:α=α(r(x)),β=β(r(x)).对于其他区域,有类似的结果. 显然,问题(1)—(3)的解u(x)满足 (16) 其中ΨSL,ΨDL分别为单双层位势: 这里G(x,y)为Helmholtz方程的基本解 定义复距离 并且令 因此可以得到 (17) 由定理1和引理1,可以得到下面结论. (18) 其中:m≥2,ε0>0, (19) (x1-y1)(x1-L1/2)>0,(x2-y2)(x2-sgn(x2)L2/2)≥0. 由引理2和定理1得 (20) 类似文献[7],可以证明: 引理3存在和k,σ,dj(j=1,2)无关的常数C>0使得: (21) (22) (23) (24) 类似文献[2]中定理3.3,可以得到如下的收敛性估计: (25) 其中:γ为(19)式所定义,m≥2,L=max(L1,L2),C>0为与k,d1,d2,ε0无关的常数. 证明由(16)和(17)式可得 再由引理3,即可得到(25)式. 文献[8]中给出的PML方法,PML问题的收敛性依赖于PML层的厚度.而本文给出的优化PML方法中,由定理2可以看出,只要ε0充分小,优化的PML解指数收敛于原问题的解,并且PML解不依赖PML层的厚度,对于较小的厚度,可以降低有限元的计算量.各向异性的优化PML方法为不连续波数的散射问题提供了一种方便灵活的计算方法.在后续工作中将使用此方法求解不连续波数的散射问题.1 各项异性的优化PML方法的构造
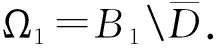
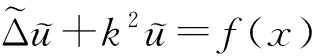


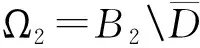

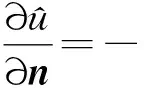
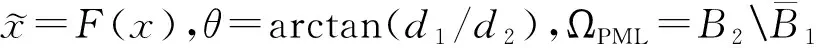
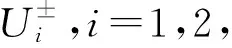




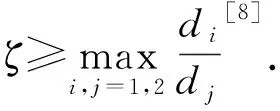
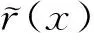





2 优化PML方法的收敛性