盘式和柱式飞轮转子系统临界转速分析

任正义，周元伟，马燕芹，黄 同



盘式和柱式飞轮转子系统临界转速分析

任正义1，周元伟2，马燕芹3，黄 同2

（1哈尔滨工程大学工程训练国家级实验教学示范中心，黑龙江 哈尔滨 150001；2哈尔滨工程大学机电工程学院，黑龙江 哈尔滨 150001；3中国科学院自动化研究所，北京 100080）

针对飞轮储能系统升降速实验中极限转速为9300 r/min，小于飞轮储能的最高工作转速15000 r/min，这会大幅降低飞轮储能系统的最大储能量。为提高飞轮储能实验中极限转速，从结构设计角度出发，采用理论公式分析、SAMCEF Rotor有限元仿真分析并结合实验数据来研究盘式飞轮转子和柱式飞轮转子的临界转速分布规律及其稳定性。分析发现，质量相同、结构不同的盘式飞轮转子其二阶临界转速远远超过柱式飞轮转子，两者的一阶临界转速相同。根据不同工作转速和储能量要求的飞轮转子，采取不同的结构方案，确保其达到工作转速要求并稳定运行。

飞轮储能；SAMCEF Rotor；临界转速；稳定性

伴随着全球工业化和信息化发展的日新月异，电力在生产和生活中的需求也在猛增，能源需求和消耗在增加，而煤炭和石油等不再生资源日益稀缺，因此能源问题已经成为限制经济快速持续发展的主要因素之一[1]。飞轮储能是一种比较新颖的储能方式，因具备能源损耗少、能量转换效率高、清洁环保、可利用周期长、维护方便等优点，表现出广阔的应用前景，已逐步应用于改善太阳能、风能的存储、航空航天器材的能量供应、区域电力质量的优化与电网峰谷调节、新能源油电混动汽车、不间断电源（UPS）等多个能源有效利用方面。

2010年美国波音公司研制出高温超导磁悬浮轴承支承的储能飞轮轴系转子，并应用于民航飞机项目，国内对飞轮储能研究起步较晚[2]，自20世纪90年代，中国科学院电工研究所和清华大学开始适应于飞轮储能原理的验证性研究[3]，2010年哈尔滨工程大学开始基于风力发电的飞轮储能关键技术研究，分别研制了储能量为600 W·h和10000 W·h的飞轮储能系统，高转速、高储能密度是飞轮储能的主要特点，因此研究飞轮转子系统的临界转速和高转速下稳定性是其结构设计中最重要的内容之一。

1 飞轮转子系统结构组成

600 W·h飞轮储能系统采用的是左右对称的立式布局，该系统主要由电机/发电一体机、飞轮、推力盘、径轴向电磁轴承和保护轴承等组成。飞轮转子系统是储能部件，也是整个系统中最核心的部分，如图1所示。其基本原理是通过两个径向电磁轴承和一个轴向电磁轴承实现飞轮轴系在平衡位置的稳定悬浮，由电发一体机完成机械能和电能的相互 转化[4]。

图1 飞轮转子系统模型和结构简图

2 飞轮储能实验极限转速分析

2.1 临界转速求解

通过有限元软件SAMCEF Rotor求解得到某飞轮转子的campbell图，campbell图中横坐标为飞轮转子转速，纵坐标为飞轮转子的涡动频率，过原点且斜率为1直线与其它曲线交点为临界转速点，即容易发生共振的不稳定转速[5]，见图2。

经过计算得到飞轮转子系统的前四阶临界转速从小到大为：2563 r/min、11063 r/min、29721 r/min和95917 r/min，与其对应前四阶临界转速下阵型如图3所示，其中图3(a)、3(b)分别对应刚性转子的平动、锥动振型，图3(c)、3(d)分别对应柔性转子的一阶弯曲、二阶弯曲振型。按照设计要求，本文飞轮转子系统为刚性转子，即其最高工作转速（15000 r/min）不能超过一阶弯曲临界转速（29721 r/min）20%的共振范围。

图2 飞轮转子系统campbell图

图3 飞轮转子系统振型图

2.2 实验数据分析

实验中的飞轮储能系统如图4所示。

飞轮转子系统的转速由电机提供，通过电机和电磁轴承联调，实验中飞轮转子实现最大极限转速9300 r/min时，电磁轴承开始报警，电机驱动器也出现瞬间的极限电流，得到飞轮转子转速和电机驱动电流关系如图5所示。

图4 飞轮储能系统实验平台

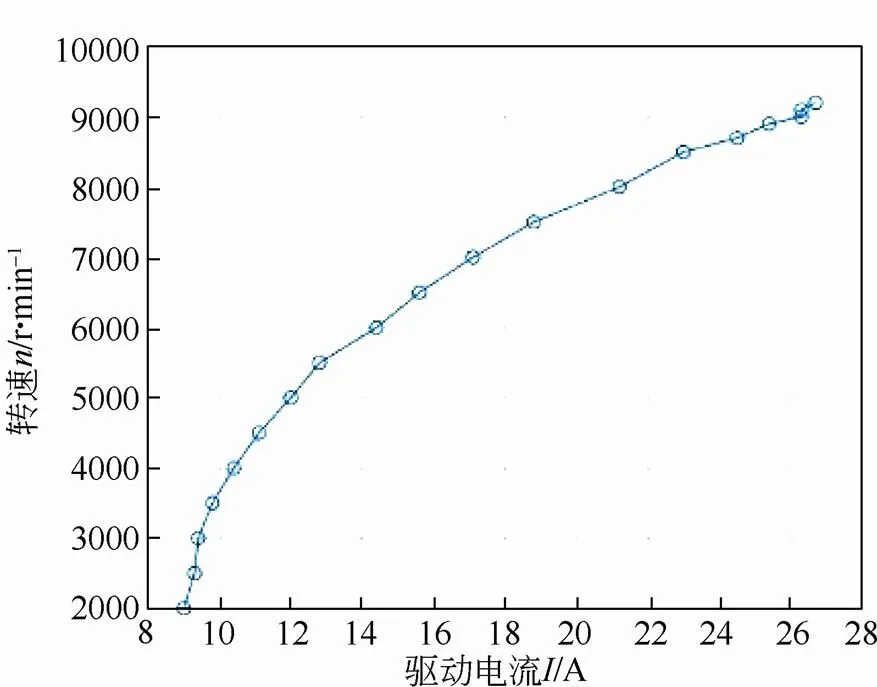
图5 电机驱动电流和转子关系图

飞轮储能转子转速达到9300 r/min后无法继续提升的原因分析：一是位移传感器信号缺乏滤波，导致信号中的噪音无法消除，电磁轴承出现不可控现象；二是转速9300 r/min已经进入二阶临界转速[11063 r/min，图3(b)]20%的共振范围内[6-7]，造成转子比较大的偏移。针对后者可能的原因，应提高飞轮转子的二阶临界转速，确保工作转速与其之间有足够的安全裕度，在下文中主要针对后者提出结构设计改善的思路。

根据实验数据，绘制的飞轮转子轴心轨迹和 频域振动分别如图6、图7所示。通过轴心轨迹 图6可以看出，在转速达到9100 r/min时，飞轮转子相对平衡位置出现了较大的偏移，上、下电磁轴承支承中心偏移量分别为0.253～0.296 mm、0.219～0.292 mm，偏移量已经非常接近最大气隙 值0.3 mm，说明转子和定子处于即将产生摩擦的临界状态。虽然飞轮转子偏移量较大，但是其振动范围较小，这是由于高转速下陀螺自定心效应开始 显现。

图7 径向磁轴承转子振动频域图（9100 r/min）

通过振动频域图7可得低频处有一个较大的振幅，这是由于傅里叶展开频谱上的最低频率峰值（通常是最高振幅）是原始信号的频率，所以忽略此处低频的振幅。在频域振动图中没有发现包括不平衡响应（151.7 Hz）在内的明显外部激励，说明外部激励对转子造成偏移的影响非常小。

3 盘式和柱式飞轮转子临界转速分析

3.1 刚性飞轮转子解耦振动

存在不平衡和无阻尼无外力的飞轮转子系统中的自由振动由以下运动方程来控制（考虑陀螺力矩，忽略外力和阻尼）[8-10]

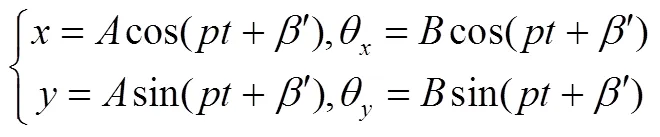
把上式代入式(1)，比较左右两个项的系数，得到

通过消除和，得到下面的频率方程

通过式(3)和式(4)可以求得特征根为

图8 飞轮转子临界转速分布图

图9 刚性飞轮转子临界转速图

Fig.9 Critical speed diagram of a rigid flywheel rotor

3.2 SAMCEF Rotor有限元分析

飞轮转子系统虚拟样机结构利用软件SOLIDWORKS对主要零部件进行三维造型并装配，因主要分析不同转动惯量比对稳定性影响，为计算的快速性和对比的便捷，删减了推力盘、黄铜螺栓、垫片、电机转子等，并忽略倒角等特征，同时定义了各部件的密度、弹性模量、泊松比等材料特性，如表1所示。

表1 模型材料属性

为研究不同转动惯量比的飞轮转子系统高速旋转的稳定性，设计了两种材料相同、质量相同、支承方式相同，但转动惯性比不同的转子轴，转动惯量比为赤道转动惯量与极转动惯量之比，两种模型基本属性见表2，并使用专业转子动力学分析软件SAMCEF Rotor分析了两种转子的前三阶临界转速及涡动频率振型。

表2 两种模型基本属性

将盘式和柱式三维模型导入SAMCEF Rotor软件中，在SAMCEF Field环境下，用Rotor Dynamics模块进行分析，为确保转子各部件在工作中不发生松动，所有部件间连接方式采用glue，同时在转子两端添径向轴承的约束，等效刚度系数设置为2.1×106N/m，等效阻尼系数为55 N·s/m，为了平衡时间、计算量、精度三者关系，采用四面体网格自由划分网格，大小为6 mm，划分网格后如图10。

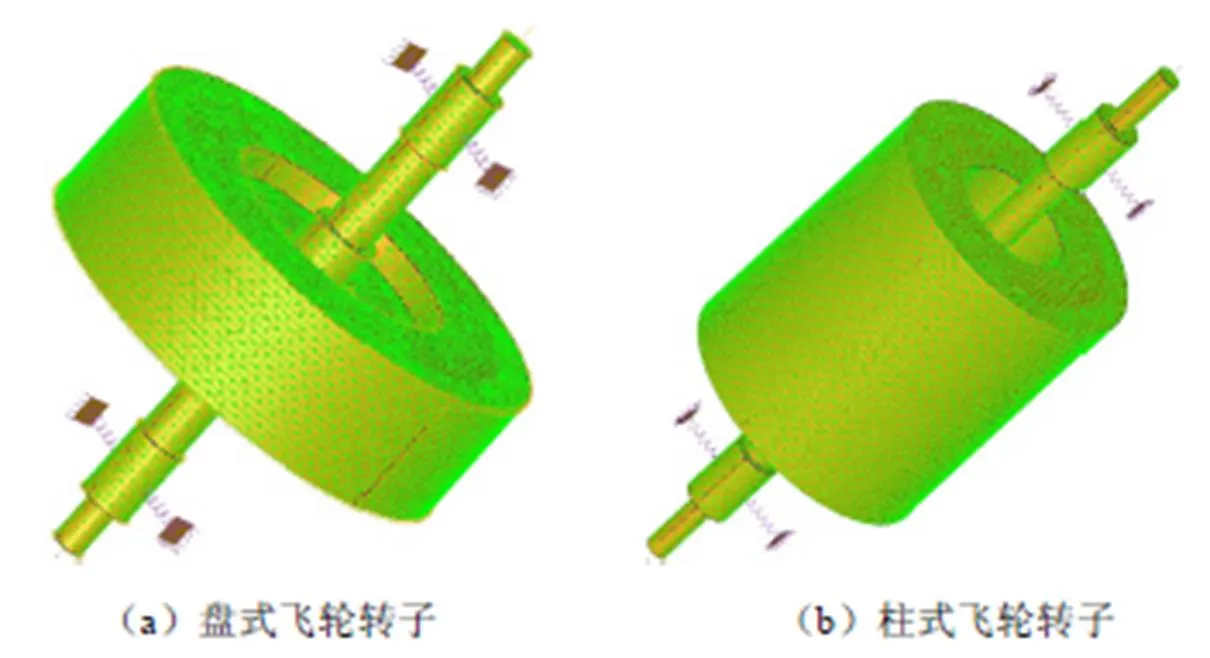
图10 网格划分

图11 坎贝尔图

仿真分析后，得到坎贝尔图如图11所示，临界转速如表3所示。

表3 两种模型临界转速计算结果

由表3得知，盘式飞轮转子和柱式飞轮转子的一阶临界转速相同，都是2615 r/min，这是由于它们的质量相同，支承方式和特性相同，所以两者的一阶平动振型转速相同，这与式(5)的分析一致；其次，前者二阶临界转速高于后者，在3.1节解耦振 动分析中，盘式转子比柱式转子系统在高转速处少了一个临界转速主振动点，有限元求解结果和刚性转子动力学方程解耦结果一致。

4 结 论

通过分析表明，在质量、材料、支承特性相同的情况下，盘式飞轮转子比柱式飞轮转子的二阶临界转速更高，由于两者一阶临界转速大致相同，因此盘式飞轮转子稳定转速区间（介于一阶临界转速和二阶临界转速之间）也更大，其储能量也远高于柱式飞轮转子，但极转动惯量较大，对电磁轴承控制性能要求较高。本文试验的600 W·h飞轮转子是柱式结构，实验中极限转速9300 r/min已经进入二阶临界转速20%的共振范围，这是不稳定因素之一。

通过动态试验和有限元仿真分析，针对600 W·h储能飞轮系统，当工作转速较低（<10000 r/min），飞轮转子可设计成柱式结构，在满足储能量要求基础上，利于电磁轴承的设计和安装。当工作转速较高（>10000 r/min），可设计成盘式结构，工作转速应在一阶和二阶临界转速之间，并避开临界转速20%的共振，为确保其稳定性，电磁轴承设计中需要考虑陀螺效应的影响。

[1] STRASIK M, HULL J R, MITTLEIDER J A, et al. An overview of boeing flywheel energy storage systems with high-temperature superconducting bearings[J]. Superconductor Science and Technology, 2010, 23(3): 13-17

[2] SHINICHI M, KENGO N, HISAKI S, et al. Development of superconducting magnetic bearing for 300 kW flywheel energy storage system[J]. IEEE Transactions on Applied Super Conductivity , 2017, 27(4): 1-4.

[3] 戴兴建, 卫海岗, 沈祖培. 飞轮储能转子轴承系统动力学设计与试验研究[J]. 机械工程学报, 2003, 39(4): 97-101.

DAI Xingjian, WEI Haigang, SHEN Zupei. Dynamics design and experimental study of flywheel energy storage rotor bearing system[J]. Chinese Journal of Mechanical Engineering, 2003, 39(4): 97-101.

[4] 刘静娜. 飞轮储能系统磁悬浮轴承—转子动力学特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.

LIU Jingna. Study on dynamic characteristics of magnetic bearings-rotor of flywheel energy storage system[D]. Harbin: Harbin Engineering University, 2014.

[5] 周传月. SAMCEF有限元分析与应用实例[M]. 第2版. 北京：机械工业出版社, 2015.

ZHOU Chuanyue. SAMCEF finite element analysis and application example[M]. 2nd Ed. Beijing: Machinery Industry Press, 2015.

[6] 《航空发动机手册》总编委会. 航空发动机设计手册, 第19册, 转子动力学及整机振[M]. 北京: 航空工业出版社, 2000.

Aero-Engine Handbook editorial board. Aero engine design handbook, Volume 19, Rotor dynamics and machine vibration[M]. Beijing: Aviation Industry Press, 2000.

[7] 休译尔.液体火箭发动机现代工程设计[M]. 朱宁昌译. 北京: 中国宇航出版社, 2003.

HUGH D K. Modern design of liquid rocket engines[M]. ZHU Ningchang,trans. Beijing: China Aerospace Press, 2003.

[8] YUKIO I, TOSHIO Y. Linear and nonlinear rotor dynamics: A modern treatment with applications[M]. USA: John Wiley Sons, 2013.

[9] JIRL K, PAVEL N, ONDREJ M, et al. The influence of rotor unbalance on turbocharger rotor dynamics[J]. Journal of Middle European Construction and Design of Cars, 2016, 13(3): 8-13.

[10] JIVKOV V S, ZAHARIEV E V. High-speed rotor analytical dynamics on flexible foundation subjected to internal and external excitation[J]. Journal of Theoretical and Applied Mechanics, 2016, 46(4): 3-18.

Critical speed analysis of disc and column flywheel rotor system

REN Zhengyi1, ZHOU Yuanwei2, MA Yanqin3, HUANG Tong2

(1National Engineering Experimental Teaching Demonstration Center, Harbin Engineering University, Harbin 150001, Heilongjiang, China;2College of Mechanical and Electrical, Harbin Engineering University, Harbin 150001, Heilongjiang, China;3Institute of Automation, Chinese Academy of Sciences, Beijing 100080, China)

For the flywheel energy storage system, the maximum speed of the flywheel energy storage system in experiments is 9300 r/min, which is less than the maximum rated speed of 15000 r/min. This will greatly reduce the maximum energy storage of the flywheel energy storage system. In order to improve rotor dynamics structural design, theoretical formulae analysis, finite element analysis of SAMCEF Rotor are used to study the critical speed distribution and stability of disc rotor and column flywheel rotor with combination of experimental data. The analysis result indicated that the second-order critical speed of the disc flywheel rotor with the same mass and different structure far exceeds the column-type flywheel rotor, and the first-order critical speed of the two types of flywheel is almost the same value. According to the different working speed and energy requirements of the flywheel rotor, different structural solutions should be adopted to ensure the requirements of the operating speed and stable operation.

flywheel energy storage; SAMCEF Rotor; critical speed; stability

10.12028/j.issn.2095-4239.2018.0076

TH 133.3；O 313.7

A

2095-4239（2018）05-821-07

2018-05-21；

2018-06-28。

国家高技术研究发展计划（2013AA050802）。

任正义（1962—），男，教授，主要研究方向为飞轮惯性储能关键技术，E-mail：renzhengyi@hrbeu.edu.cn；

周元伟，硕士研究生，主要研究方向为飞轮惯性储能关键技术，E-mail：zhouyuanwei@126.com。