针对并网型风储微网的飞轮储能阵列系统控制方法

郭 伟，张建成，李 翀，苏 浩



针对并网型风储微网的飞轮储能阵列系统控制方法

郭 伟1，张建成1，李 翀2，苏 浩1

（1华北电力大学电气与电子工程学院，河北 保定 071003；2哈尔滨工程大学储能技术与应用研究所，黑龙江 哈尔滨 150001）

由于新能源发电存在波动性和间歇性，其大量接入时会给电网运行带来新的困难，而利用储能技术提高新能源的可调度性是当前研究的热点。为缓解新能源并网对电力系统的不良影响，针对并网型风储微网提出了一种基于飞轮储能阵列系统的分层优化控制方法，上层优化中心根据功率缺额和各台飞轮的转速建立相应充/放电优化模型，并求解相应飞轮的功率参考值；下层飞轮控制器采用双模双环控制方法，实现飞轮转速和输出功率的控制，最后通过MATLAB/Simulink仿真验证了所提控制方法的有效性和可行性。

无刷直流电机；飞轮储能阵列；风电；交流微网；功率缺额

受制于自然条件，新能源发电具有波动性和间断性的特点，当其大量接入时会给电网的调度运行带来诸多困难。为缓解该负面影响，同时增加电网的包容性，储能技术应用成为当前研究热点。除传统的抽水蓄能电站以外，目前我国电网中较为常见的储能设备是电池储能系统，相比于前者电池储能具有能量密度高、不受地形条件限制等优点，但其功率密度低、循环寿命短的缺点导致系统整体经济性较差，并且存在废弃电池回收的问题[1]。在其它众多储能技术中，飞轮储能具有转换效率高（85%～90%）、响应速度快（ms级）、使用寿命长（20年左右）等优点，虽然初期安装成本较高，但维护保养费用很低，是一种市场前景广阔的储能技术[2-3]。

飞轮储能一般是指电能与动能之间的双向转换，通过电力电子装置控制飞轮电机的旋转速度，实现升速储能和减速发电的功能，灵活的吞吐能力使该技术在平滑新能源出力以及电网调频方面具有一定的应用需求[4-6]。飞轮储能系统所储存能量受限于飞轮本体的转动惯量和角速度，从目前飞轮材料和高速电机的研制进展来看，大幅提高单体飞轮的能量密度较为困难。而将多个飞轮储能模块并联组成规模较大的阵列系统，则是一种可行的大容量集成方案[7-9]。为解决风电输出功率可调度性差的缺点，本文提出了一种利用飞轮储能阵列系统进行功率缺额补偿的分层控制策略，上层优化中心采集各个飞轮单机的转速和风功率预测差值，通过求解相应优化问题确定阵列系统内部的功率分配；下层飞轮控制器采用双模双环控制，外环采用转速/功率PI控制，内环采用电流滞环跟踪控制，最终实现飞轮单体的功率跟踪和转速稳定。

1 并网型风储微网

本文所研究的并网型风储微网结构如图1所示，由风电机组、多台飞轮单机、负荷、外部电网以及电力电子装置组成，其中多台飞轮单机构成飞轮储能阵列系统。运行时根据风功率预测、负荷预测和外部电网调度计划进行微网层日前调度，当日则根据超短期预测值滚动调整计划出力。由于风电较强的随机性，不可能实现短时间尺度的精确调度，则可以利用飞轮储能阵列系统实现跟踪计划出力。当飞轮储能阵列系统容量较为充足时，外部电网可以采用定联络线控制（相当于电流源），优先由飞轮储能阵列系统修正功率缺额；当飞轮储能阵列系统达到各自SOC上、下限时，则由外部电网承担多余功率。该调度策略既可以提高风电并网功率，又可以减少微网对外部电网的不良影响。

飞轮电机采用永磁无刷直流电机，其主要由电机本体（包括定子和转子），位置传感器和双向DC/AC变换器组成。在建立数学模型时，直接利用电机本身的相变量方式。假设磁路非饱和，三相绕组完全对称，不计涡流和磁滞损耗。由于转子位置的变化不影响转子磁阻的大小，所以定子绕组的自感和互感均为常数，则相绕组的电压平衡方程式可以表示为[10]

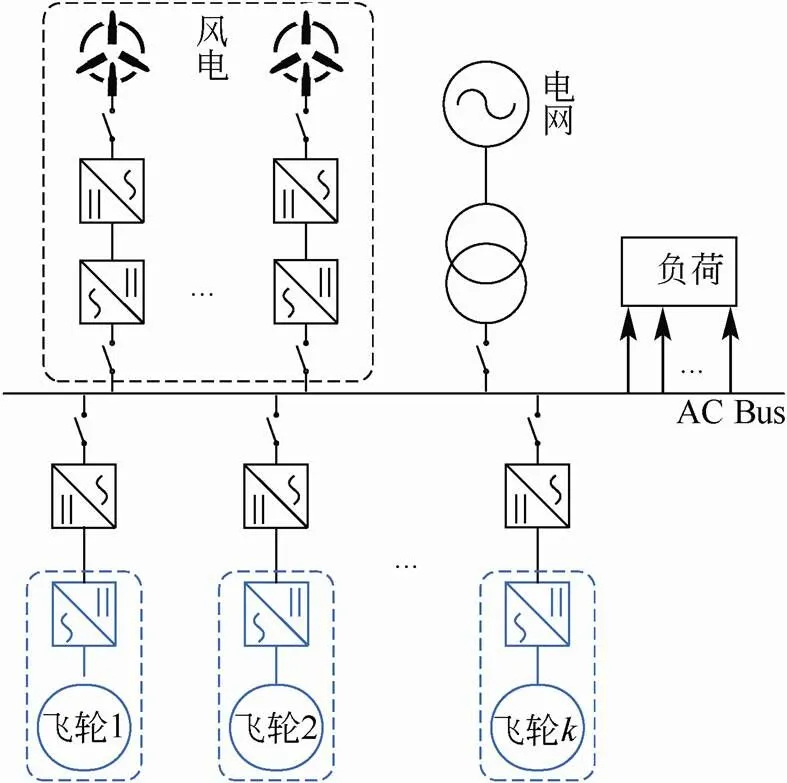
图1 并网型风储微网结构图

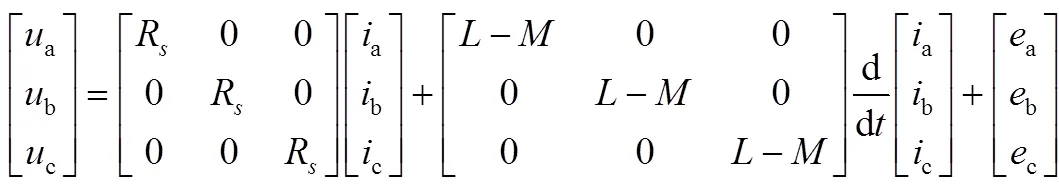
（1）

式中，abc为定子绕组相电压；s为定子绕组相电阻；abc为定子绕组相电流；abc为定子绕组相电动势；是定子绕组自感；是定子绕组互感。

其机械运动方程为

式中，为整体（包括飞轮和转子）的转动惯量；m为黏滞系数；m为转子机械角速度；e为电磁转矩。

飞轮储能系统的输出功率e为

飞轮储能系统的最大储能量max和有效储能量eff分别为

式中，max为转子机械角速度上限值；min为转子机械角速度下限值；min为角速度下限时的最小储能量。

机械角速度m（r/s）与转速（r/min）之间的关系为

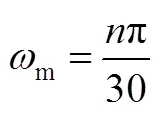
2 基于飞轮储能阵列系统的分层控制策略

2.1 充、放电优化模型

微网运行时，风电实际发出功率与计划出力之间可能存在较大偏差D，此部分功率由飞轮储能阵列系统弥补。如图2所示，上层优化中心以固定采样间隔s采集各个飞轮的转速n（=1，2…，设有台飞轮单机），微网调度中心同样以s间隔下发功率缺额D至优化中心，然后求解式(7)、(8)所示充/放电优化模型，确定各台飞轮的参考功率P-ref。

图2 上层优化中心

目标函数遵循“能者多劳”原则，即充电时转速慢的飞轮承担最多的功率份额，而转速快的飞轮承担最少的功率份额，放电时则相反。约束条件中主要体现的是能量约束和功率守恒约束。由于采样时间s很短，假设这段时间功率缺额D保持不变。

充电优化模型

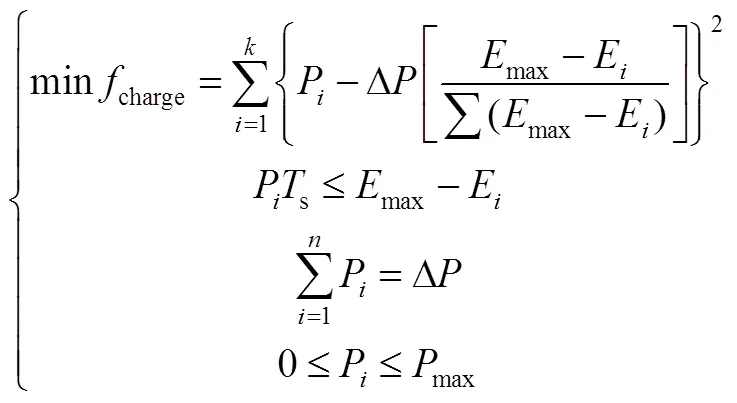
放电优化模型

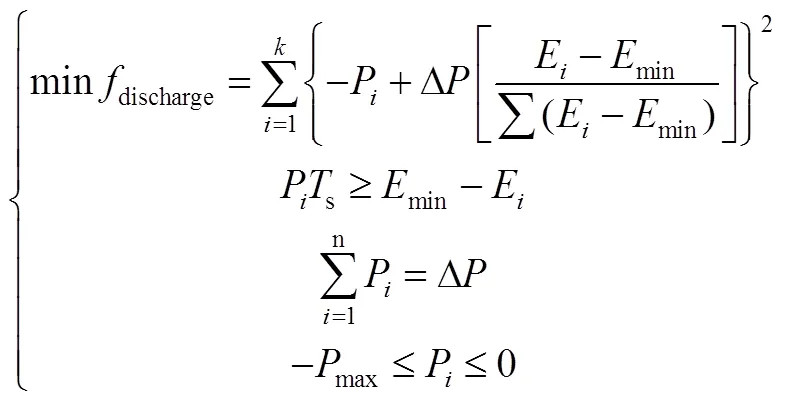
式中，P为待优化变量；D为功率缺额，D>0表示飞轮需充电，D<0表示飞轮需放电；max为飞轮功率上限；E为采样时刻飞轮单机所储存的 能量。

2.2 飞轮双模双环控制器

飞轮控制器采用双模双环控制，外环为转速/功率PI控制，如图3所示。当飞轮功率参考值P-ref不为0，且未达到飞轮转速上/下限时，为功率环模式，飞轮以参考功率输出；而当功率参考值P-ref为0，或达到飞轮转速上/下限时，切换为速度环模式，维持飞轮转速恒定。

图3 外环转速/功率PI控制

内环采用电流滞环跟踪控制[11-12]，如图4所示。外环的输出为单相电流参考值，而由电机反馈的电流为三相值，彼此无法进行比较，霍尔信号转换模块可以根据转子位置，将电流参考值分配到三相上进行处理。电流滞环跟踪控制是通过设定合适的滞环环宽，使实际电流跟随参考电流变化，从而得到更理想的实际电流波形，本文采用delay模块来设定环宽。

图4 内环电流滞环控制

3 仿真与分析

采用MATLAB/Simulink建立模型，由3台参数相同的飞轮单机组成阵列系统，电机为永磁无刷直流电机；转动惯量为0.016 kg·m2；极对数为4，定子绕组相电阻s为0.1W，定子相电感s为745 mH，摩擦系数为0.0005 N·m·s，磁链为0.023875 V·s；最大输出功率8 kW，转速上限为12000 r/min，转速下限为4000 r/min；飞轮单机直流侧电压为 500 V；外环转速PI控制器参数pv=10.7，Kv=0.1；外环功率PI控制器参数pp=0.1，Kp=10；滞环环宽=0.1；采样时间s为500 ms。直接采用一段时长为10 s的功率缺额数据进行仿真验证，如图5所示曲线，其中圆圈为实际采样点。

上层优化中心根据三台飞轮的转速和功率缺额优化出的功率指令如图6所示，飞轮转速变化曲线为图7。3台飞轮初始转速不同，分别为5000 r/min、8000 r/min、12000 r/min。从优化的功率指令可以看出，转速较低的飞轮1充电时承担最多的功率值，放电时承担最小的功率值，如红色虚线所示，且随着飞轮储能阵列的运行，3台飞轮的转速趋于相同；飞轮3初始转速处于上限12000 r/min，在0～1.5 s时无法继续吸收电能，保持转速恒定；另外在2.5 s时刻优化功率指令均为0，3台飞轮的转速均保持不变。

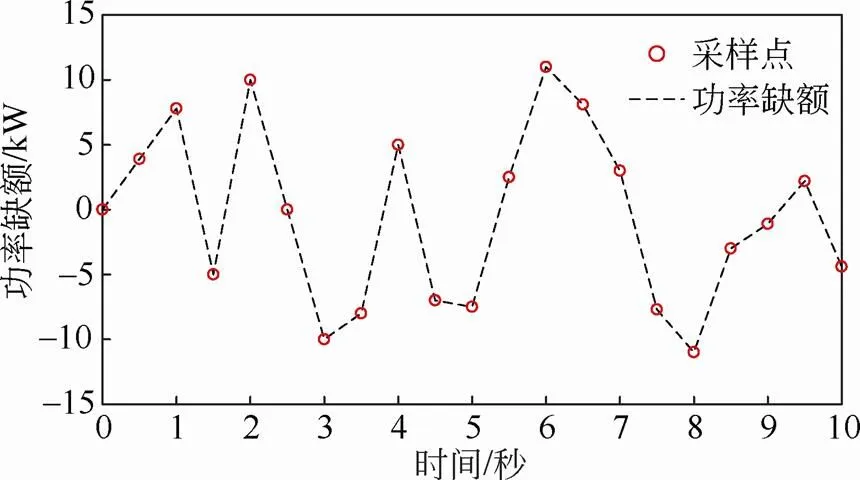
图5 功率缺额P数据

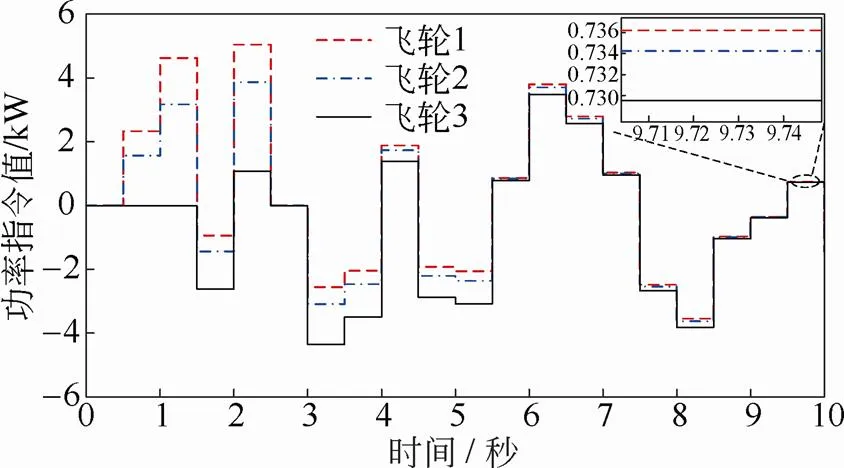
图6 功率优化结果

图7 飞轮转速

图8为3台飞轮单机的实际输出功率曲线，可以看出飞轮控制器较好的跟踪所优化的功率指令，但仍然存在一定的超调量，这主要是由于不同外环PI控制模式间切换所造成的。

4 结 论

本文针对并网型风储微网，将飞轮储能阵列系统作为能量缓冲环节，为实现风电计划出力跟踪提出了一种分层优化控制方法，上层优化中心通过求解相应优化模型确定下层控制器的参考值，下层飞轮控制器采用双模双环控制方法实现飞轮转速/功率的调节。最后利用MATLAB/Simulink建立相应数学模型，仿真结果表明在功率缺额波动变化时，所设计控制方法具有较好的控制效果。

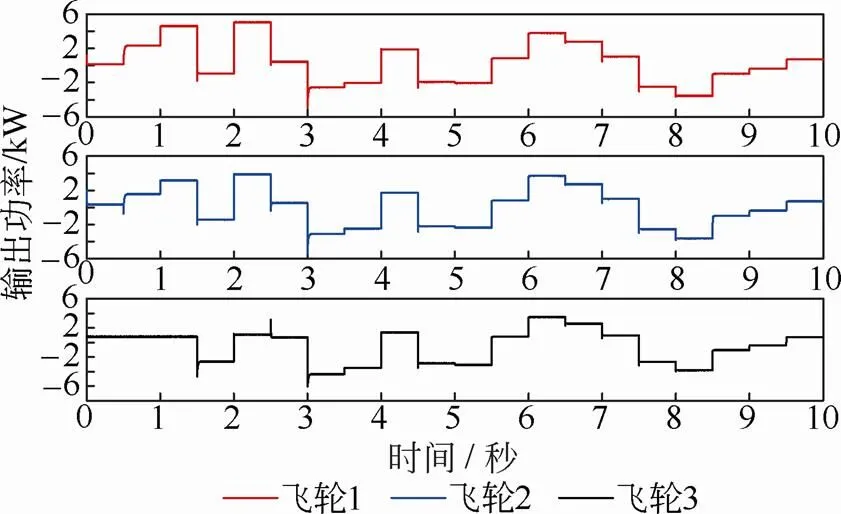
图8 飞轮输出功率

[1] AMROUCHE S O, REKIOUA D, REKIOUA T, et al. Overview of energy storage in renewable energy systems[J]. International Journal of Hydrogen Energy, 2016, 41(45): 20914-20927.

[2] MOUSAVI S M G, FARAJI F, MAJAZI A, et al. A comprehensive review of flywheel energy storage system technology[J]. Renewable and Sustainable Energy Reviews, 2017, 67: 477-490.

[3] ARANI A A K, KARAMI H, GHAREHPETIAN G B, et al. Review of flywheel energy storage systems structures and applications in power systems and microgrids[J]. Renewable and Sustainable Energy Reviews, 2017, 69: 9-18.

[4] SEBASTIÁN R, PEÑA ALZOLA R. Flywheel energy storage systems: Review and simulation for an isolated wind power system[J]. Renewable Sustainable Energy Reviews, 2012, 16(9): 6803-6813.

[5] HEARN C S, LEWIS M C, PRATAP S B, et al. Utilization of optimal control law to size grid-level flywheel energy storage[J]. IEEE Transactions on Sustainable Energy, 2013, 4(3): 611-618.

[6] 孙春顺, 王耀南, 李欣然. 飞轮辅助的风力发电系统功率和频率综合控制[J]. 中国电机工程学报, 2008, 28(29): 111-116.

SUN Chunshun, WANG Yaonan, LI Xinran. Synthesized power and frequency control of wind power generation system assisted through flywheels[J]. Proceedings of the CSEE, 2008, 28(29): 111-116.

[7] 唐西胜, 刘文军, 周龙, 等. 飞轮阵列储能系统的研究[J]. 储能科学与技术, 2013, 2(3): 208-221.

TANG Xisheng, LIU Wenjun, ZHOU Long, et al. Flywheel array energy storage system[J]. Energy Storage Science and Technology, 2013, 2(3): 208-221.

[8] CAO Qian, SONG Yongduan, GUERRERO J M, et al. Coordinated control for flywheel energy storage matrix systems for wind farm based on charging/discharging ratio consensus algorithms[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1259-1267.

[9] SARAVIA H S, PAINEMAL H P, MAURICIO J M. Flywheel energy storage model, control and location for improving stability: The Chilean case[J]. IEEE Transactions on Power Systems, 2017, 32(4): 3111-3119.

[10] 赵晗彤, 张建成. 基于滑模控制的飞轮储能稳定光伏微网离网运行母线电压策略的研究[J]. 电力系统保护与控制, 2016, 44(16): 36-42.

ZHAO Hantong, ZHANG Jiancheng. Research on bus voltage control strategy of off-grid PV microgrid with flywheel energy storage system based on sliding mode control[J]. Power System Protection and Control, 2016, 44(16): 36-42.

[11] 王欢. 飞轮储能的电机驱动控制系统研究[D]. 成都: 西南交通大学, 2012.

WANG Huan. Research on the control of a flywheel electric machine drive system for energy storage[D]. Chengdu: Southwest Jiaotong University, 2012.

[12] 王建华, 张方华, 龚春英, 等. 滞环电流控制逆变器建模及分析[J]. 电工技术学报, 2010, 25(6): 63-69.

WANG Jianhua, ZHANG Fanghua, GONG Chunying, et al. Modeling and analysis of inverter with hysteretic Current control[J]. transactions of China Electrotechnical Society, 2010, 25(6): 63-69.

Control method of flywheel energy storage array for grid-connected wind-storage microgrid

GUO Wei1, ZHANG Jiancheng1, LI Chong2, SU Hao1

(1School of Electrical and Electronics Engineering, North China Electric Power University, Baoding 071003, Hebei, China; Research Institute for Energy Storage Technology and Application, Harbin Engineering University, Harbin 150001, Heilongjiang, China)

Due to the fluctuation and intermittent nature of renewable energy, they massive access will bring new difficulties to the power grid operation. Improving the scheduling of renewable energy by using energy storage technology is the focus of current research. In order to mitigate the bad effect of renewable energy generation on power grid, a layered optimal control method based on flywheel energy storage array is proposed for grid-connected wind-storage microgrid. The upper optimization center establishes the corresponding charge/discharge optimization model according to the power shortfall and the speed of each flywheel, and solves the power reference value of the corresponding flywheel. The lower flywheel controller adopts dual-mode double loop control method to realize the control of flywheel speed and output power. Finally, the effectiveness and feasibility of the proposed control method are validated by MATLAB/Simulink simulation.

BLDC; flywheel energy storage array; wind power; AC microgrid; power shortage

10.12028/j.issn.2095-4239.2018.0013

TM 614；TM 313

A

2095-4239（2018）05-810-05

2018-01-22；

2018-01-31。

国家自然科学基金项目（51177047），河北省科技支撑计划项目（16214504D），黑龙江省科技攻关计划（GZ11A208）及中央高校基本科研业务费专项资金项目（2018QN072）。

郭伟（1989—），男，博士研究生，主要研究方向为新能源发电及储能技术，E-mail：guoweincepu@126.com。