氢化杂质和厚度效应对高斯势量子点中二能级体系量子跃迁的影响∗

白旭芳 赵玉伟 尹洪武 额尔敦朝鲁

1)(内蒙古民族大学物理与电子信息学院,通辽 028043)2)(河北科技师范学院凝聚态物理研究所,秦皇岛 066004)(2018年2月19日收到;2018年5月15日收到修改稿)

1 引 言

近年来,量子点的奇特光学性质和输运特性持续受到人们的重视,已成为材料科学和凝聚态物理中的一个热点领域,出现了许多新的实验研究[1−4]和理论研究[5−8]工作报道.但仍有一些有价值的课题亟待研究.1)关于量子点存在厚度的问题.不难看出,人们对量子点的理论研究大多都未考虑量子点的厚度所带来的影响,其结果无疑是比较粗糙的.2)关于量子点限定势的描写.在许多研究中,单参量抛物线型限定势阱被用来描述量子点中电子的限定势[9−12].然而,抛物线型限定势阱既没有有限的深度也没有范围可言,是一种过于简化了的模型,不能很好地反映真实的限定势.一些实验结果的限定势应采用非抛物形的阱状势[13],如密度矩阵势或非对称三角势[14]、高斯函数型限定势阱[15]等,其中高斯函数型限定势阱是一个很好的近似,它平滑并具有有限深势阱和有限的阱宽.Adamowski等[16]研究了在假想高斯函数型限定势阱束缚下的两电子量子点系统,并讨论了它的抛物近似.Xie[17]计算了高斯函数型限定势阱中两电子量子点的能谱.谷娟和梁九卿[13]利用数值矩阵对角化的方法计算了高斯函数型限定势束缚下施主中心量子点系统能谱并讨论了其特性.但这些工作均未考虑介质的极化效应.3)关于极化效应对电子态的影响.当计及量子点厚度时,由于强量子受限效应的存在,使得极化效应表现得更为明显[18,19],毫无疑问,量子点的厚度引起的介质的极化效应对量子点中电子态的影响不可忽视.最近,Xiao[20]研究了RbCl反对称高斯函数型限定势量子阱量子比特的电场效应,Khordad等[21]研究了非对称高斯函数型限定势量子阱中束缚极化子基态和寿命的温度依赖性.4)近几年引入高斯限定势阱研究低维结构电子态的性质在量子阱结构已有不少出色的工作报道[14,20−23],但是,相关研究在量子点结构领域甚少,尤其是研究电磁场对高斯函数型限定势量子点中电子态变迁的影响的工作尚未报道.本文在计及量子点厚度和氢化杂质束缚情形下,分别选取抛物线型限定势阱和高斯函数型限定势阱描写盘型量子点中电子的横向限定势和纵向限定势,采用Lee-Low-Pines-Pekar变分法研究了电子在外磁场作用下的量子跃迁问题.

2 理论模型与变分计算

考虑一个处于盘状量子点中与介质中的体纵光学(longitudinal optics,LO)声子场相互作用的电子.建立笛卡尔坐标系,盘的中心轴线在Oz轴上,底面处于垂直于Oz轴的x-y平面上.在坐标原点处掺入一氢化杂质并施加沿z轴方向的磁场B.采用抛物线型限定势阱

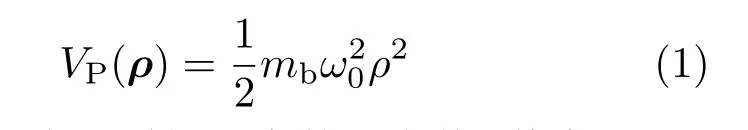
描述电子在垂直于磁场方向的限定势,其中mb是电子的带质量,ρ是电子在x-y平面上的位矢,ω0为量子点的横向受限强度,为抛物线型限定势范围;采用非对称高斯函数型限定势阱

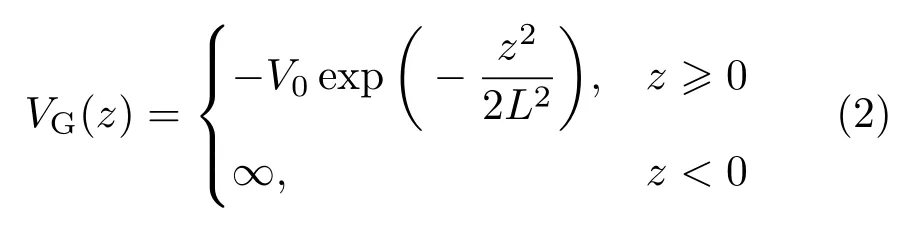
描写电子在磁场方向的限定势,其中,V0表示高斯函数型限定势阱的阱深且V0＞0;L表示其阱宽,亦称量子点的厚度.这样,磁场中量子点内电子-氢化杂质-LO声子场相互作用体系的哈密顿量可以写为[20,21]

式中,VC(r)=−e2/(ε∞r)为库仑势,其余各量的物理意义与文献[20,21]相同.

为利用变分技术得到体系的能量本征值和本征函数,首先,将哈密顿量H右边写成两部分

这里

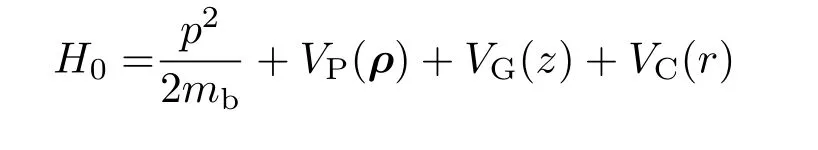
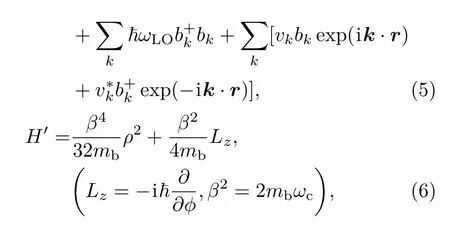
式中ωc=2eB/(mbc)为磁场的回旋频率,B为磁感应强度.然后,再讨论变分函数U−1H0U在|Φ〉态中的期待值问题,按照变分原理,

这里

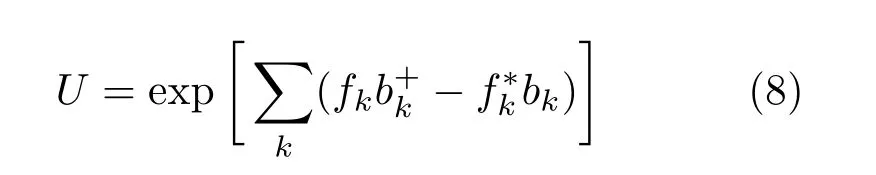
是Lee-Low-Pines幺正变换[24],其中,fk和f∗k为变分参数,|Φ〉是体系的试探波函数.假设对于体系的基态和第一激发态,高斯函数近似成立,则依据Pekar类型变分法[25−27],分别选取体系的基态试探波函数|Φ0〉和第一激发态试探波函数|Φ1〉为

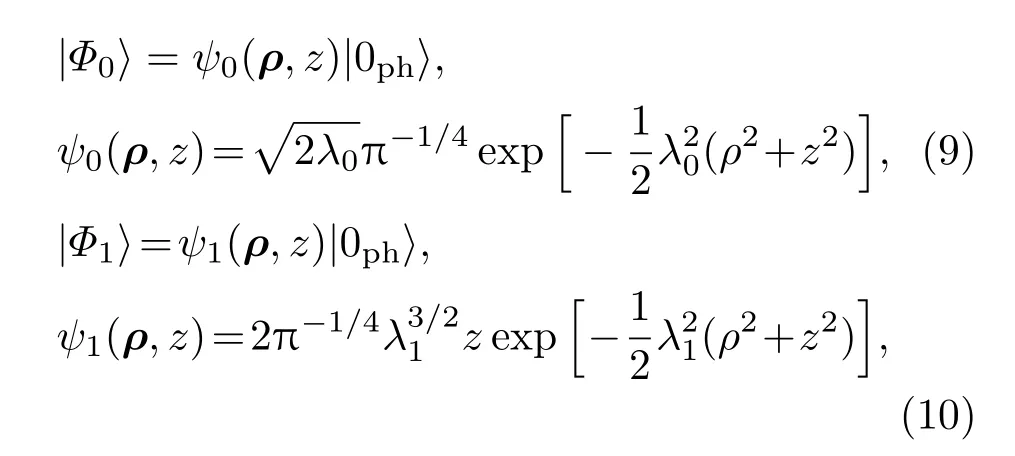
其中λ0和λ1为变分参数;ψ0(ρ,z)和ψ1(ρ,z)分别表示电子轨道运动的基态和第一激发态试探波函数;|0ph〉是声子的真空态,由bk|0ph〉=0确定.

将(5)式和(8)—(10)式代入(7)式中,可分别确定变分参数fk(λ0)和fk(λ1)为:

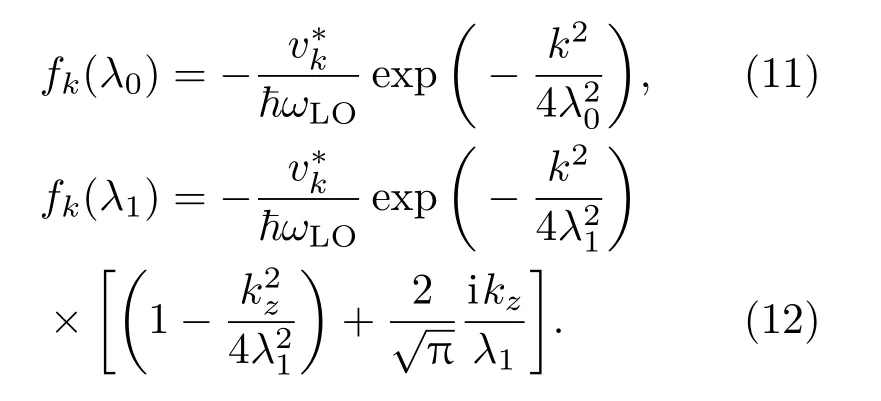
利用这些变分参数,并经过冗长的计算,得到电子-氢化杂质-LO声子相互作用体系的基态(第一激发态)平均声子数N0(N1)和能量E0(E1)分别如下:

3 结果与讨论

为了揭示极化子的基态(第一激发态)平均声子数N0(N1)和能量E0(E1)以及跃迁概率Q随介电常数比η、磁场的回旋频率ωc、电声耦合强度α、高斯函数型限定势阱深V0和阱宽L以及振荡周期t的变化规律,我们给出了数值仿真结果,如图1—图9所示. 图中分别以rp,ωLO,(ωLO)−1和ħωLO作为长度,ωc,t和能量的单位.

图1分别描写了极化子基态和第一激发态平均声子数N0和N1在不同介电常数比η下随抛物线型限定势阱范围R0的变化.图1表明,在相同条件下,N0＞N1,这一结果符合统计物理规律.由图1可以看出,N0和N1随R0的增加而减小,这是因为随着R0的增大,电声相互作用由于粒子横向运动空间的增大而减小,导致电子周围平均声子数减小;在给定R0下,N0和N1随η的增加而增大,这是因为η越大,电子与氢化杂质间库仑势VC∝−(1−η)−1越强,由此产生的晶体附加极化增大,因而推高电子周围的平均声子数增大.

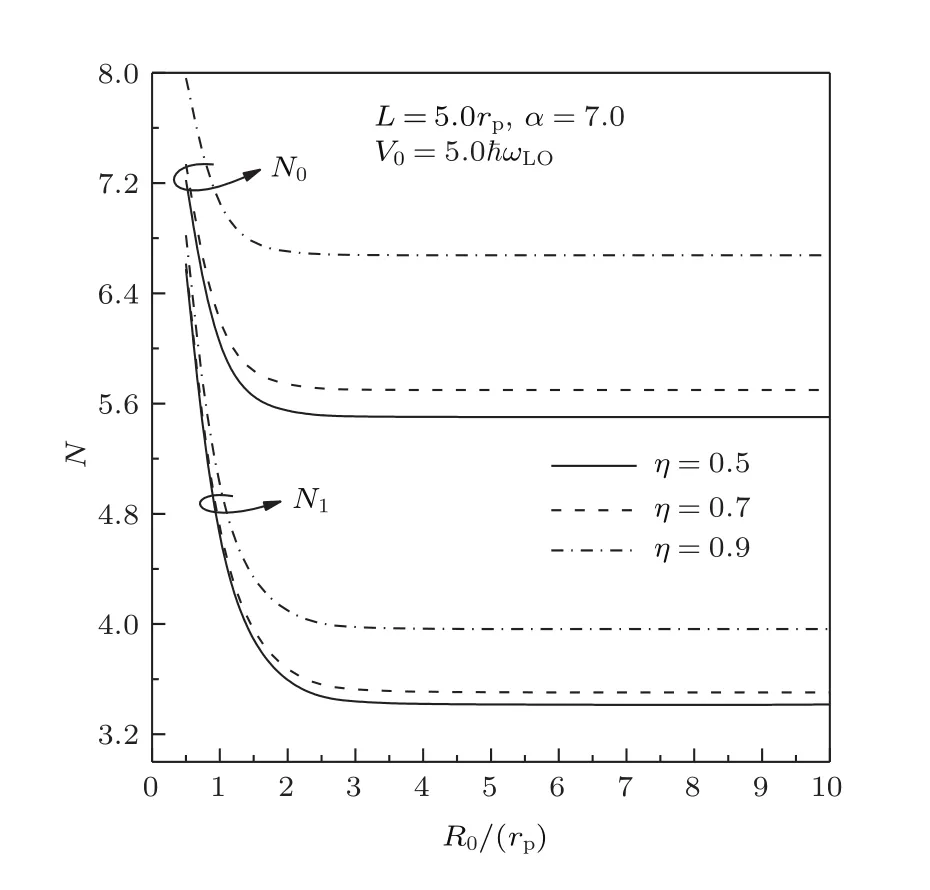
图1 平均声子数N在不同介电常数比η下随抛物线型限定势阱范围R0的变化Fig.1.Mean number of phonons N as a function of the range R0of the parabolic con finement potential well(PCPW)at different dielectric constant ratio η.

图2表示声子数N0和N1在不同阱深V0下随阱宽L的变化.由图2可以看出,在L的不同区域内,N0和N1随L的变化形式有所不同.1)当L较大时,N0和N1随L的减小而单调增大.这是因为随着L的减小,电声相互作用由于粒子纵向运动空间被压缩而增强,导致电子周围平均声子数增加.2)当L较小时,N0和N1随L的减小而增大至一个最大值.这是一种量子现象,量子点的厚度越小,量子尺寸效应越明显[18,19].3)N0和N1随L的减小而增大至一最大值后又迅速减小.这意味着当量子点的厚度很薄时,LO声子效应不再占主导作用,此时应该考虑表面光学声子或界面光学声子效应[29],这超出了本文的研究范围.4)在L给定时,N0和N1随V0的增加而增大.这是因为纵向约束势增大,意味着介质的极化增强,亦即电子周围平均声子数就增多.

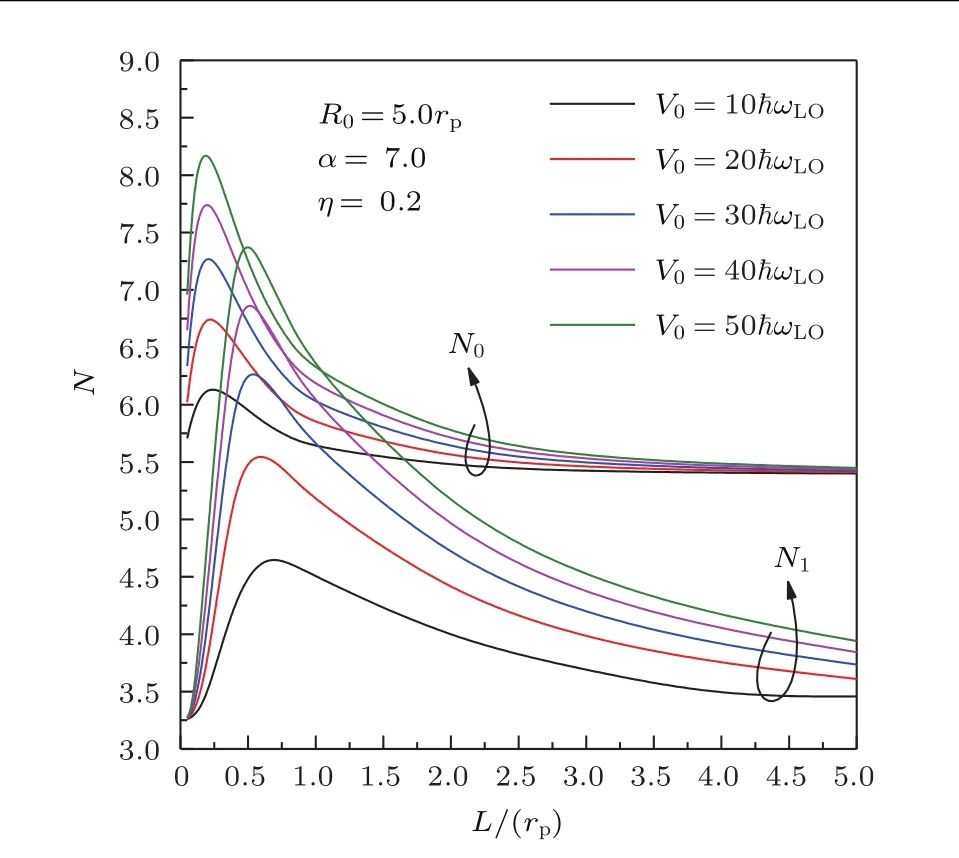
图2 平均声子数N在高斯函数型限定势阱不同阱深V0下随其阱宽L的变化Fig.2.Mean number of phonons N as a function of the well width L at different well depth V0of the asymmetric Gaussian functional con finement potential well(AGFCPW).

图3表示了基态(第一激发态)能量E0(E1)在不同介电常数比η下随抛物线型限定势阱范围R0的变化.由图3可以看出,E0和E1随R0的减小而增大,这是因为一般来说E0＜0,E1＜0,但是抛物线型限定势阱VP＞0且在给定R0下,E0和E1随η的增加而减小,这是因为在含氢化杂质的晶体或纳米结构中,电子被库仑势(VC＜0)束缚于氢化杂质中[30−32],且η越大,氢化杂质对电子的限定势VC∝−(1−η)−1越强,致使电子的能量越低.

图4描述了能量E0(E1)在不同阱深V0下随阱宽L的变化.由图4可以看出,|E0|＞|E1|,|E0|和|E1|随L的增加而增大,增大的幅度随L的增加而趋缓;同时,在给定L下,|E0|和|E1|随V0的增加而增大.这是由于高斯函数型限定势阱函数VG(z)＜0,而且|V(z)|随L或V0增加而增大所致.

图5描述了跃迁概率Q在不同介电常数比η下随抛物线型限定势范围R0的变化.由图5可以看出:Q随R0的缩小而减小.这是因为随着抛物线型限定势阱范围的减小,电子在x−y平面内的受限增大,致使电子状态的稳定性提高而改变它的难度增大.当R0较小(R0＜2.2rp)时,Q随R0的减小而减小的幅度较大;当R0较大(R0＞2.2rp)时,Q随R0的减小而减小的幅度很小.在给定R0下,Q随η的增大而减小.这是因为η越大,氢化杂质对电子的库仑限定势VC∝−(1−η)−1越强,致使电子态的变化越难.

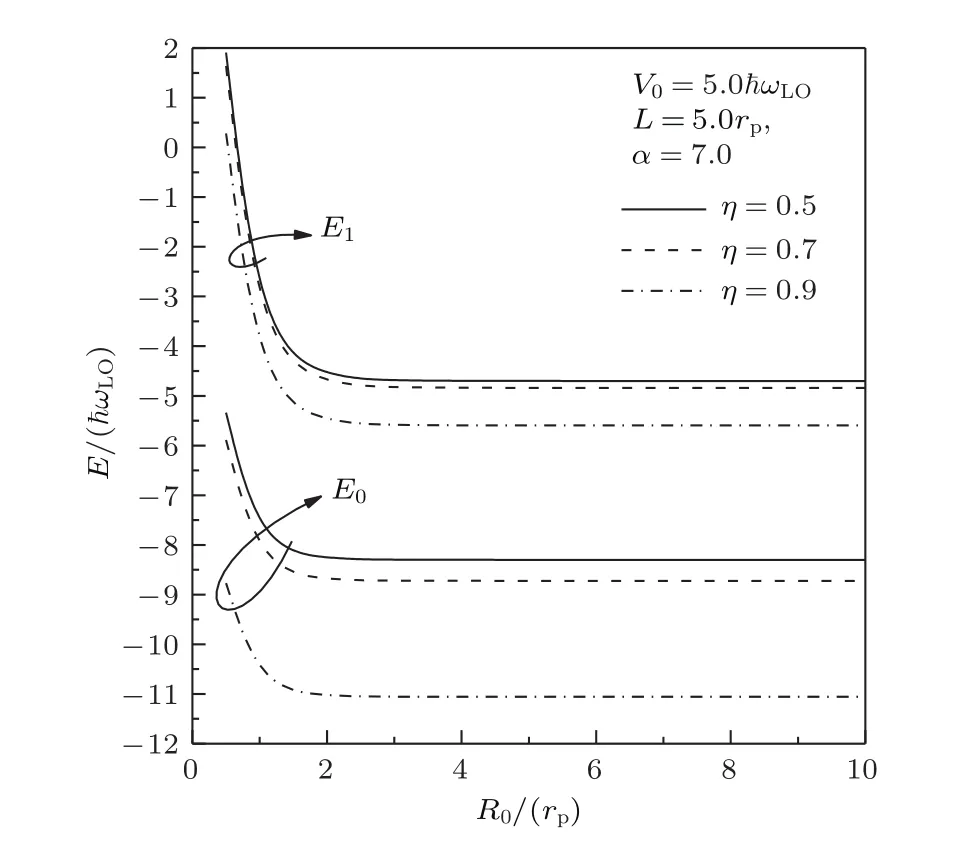
图3 基态(第一激发态)能量E0(E1)在不同介电常数比η下随范围R0的变化Fig.3.The ground(the first excited)state energy E0(E1)as a function of the range R0of the PCPW at different dielectric constant ratio η.

图4 基态(第一激发态)能量E0(E1)在不同阱深V0下随阱宽L的变化Fig.4.The ground(the first excited)state energy E0(E1)as a function of the well width L at different well depth V0of AGFCPW.

图6表示了概率Q在不同阱深V0下随阱宽L的变化.由图6可以看出,在L的不同区域内,Q随L的变化形式有所不同:当L较大(L＞1.3rp)时,Q随L的减小而单调减小,这一结果与图5所示的Q随抛物限定势范围R0的缩小而减小的规律相似;但是,当L较小(L＜1.3rp)时,Q随L的变化而振荡变化.这是一种量子现象,因为按照量子理论,阱宽L越小,量子尺寸效应越加明显.比较图6与图5不难看出,图6给出的跃迁概率Q随高斯限定势范围L的变化规律,无论从量子力学理论看,还是从实验结果[13]的检验看,都比图5给出的跃迁概率Q随抛物限定势范围R0的变化规律更加合理和符合实际.不过,当限定势范围(R0和L)的取值较大时,二者的变化规律基本一致,这是因为当z/L≪1时,高斯函数型限定势阱可以用抛物线型限定势阱近似.总之,对量子点限定势下的电子态及其变化而言,不考虑量子点的厚度所带来的影响,其结果无疑是比较粗糙的,亦即无论是对量子点输运性质还是光学性质的研究,考虑量子点厚度的影响是有实际意义的;与此同时,高斯函数型限定势比抛物线型限定势更能精确地反映量子点真实的限定势.由图6还可以看出,对于给定的L,Q随V0的增加而减小.这是因为VG(z)＜0时,V0越大,电子的能量越低,电子的状态就越稳定.

图5 跃迁概率Q在不同介电常数比η下随抛物线型限定势阱范围R0的变化Fig.5.The transition probability Q as a function of the range R0of PCPW at different dielectric constant ratio η.

图6 跃迁概率Q在高斯函数型限定势阱不同阱深V0下随阱宽L的变化Fig.6.The transition probability Q as a function of the well width L at different well depth V0of the AGFCPW.

图7表示了概率Q在不同耦合强度α下随介电常数比η的变化.由图7可以看出,Q随η的增大而减小的幅度随α的减小而增大,这是因为α越大,意味着电声相互作用越强,致使电子周围声子平均数越多,电子的自陷越深,电子态发生跃迁的难度就越大.由此可见,在研究量子点中电子态的变化时不能忽略声子(介质的极化)效应的影响.

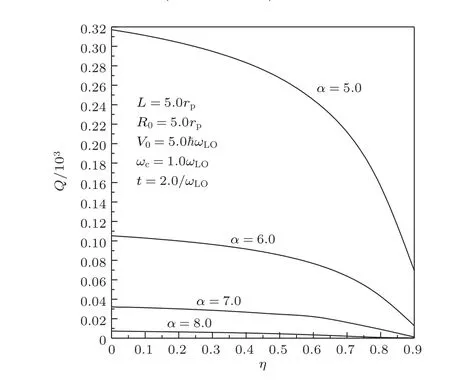
图7 概率Q在不同耦合强度α下随介电常数比η的变化Fig.7.The probability Q as a function of the dielectric constant ratio η at different electron-phonon coupling strength α.

图8描述了概率Q在不同耦合强度α下随磁场的回旋频率ωc的变化.由图8可以看出,当ωc=0时,Q=0,Q随ωc的增大而周期性振荡上升,这都表明施加外磁场是电子态发生量子跃迁的必要条件.由图8还可以看出,Q随ωc的增大而周期性振荡上升的形态受到α的显著影响,Q的振荡周期随α的增大而增加,而振荡的幅度随α的增大而减小.

图9分别表示了跃迁概率Q在不同介电常数比η和不同磁场的回旋频率ωc下随振荡周期t的变化.由图9可以看出,Q随t的变化而做周期性振荡.这是因为电子跃迁概率Q的时间演化规律由(16)式描写所致,从物理上讲,这是电子状态随时间的变化必须满足其波动方程(薛定谔方程)的必然结果.由图9不难发现,Q随t做振荡变化的形态受到η和ωc的显著影响:Q振荡的幅度和周期均随η的增大而减小;Q振荡的幅度和频率均随ωc增大而增加.

图8 概率Q在不同耦合强度α下随磁场的回旋频率ωc的变化Fig.8.The probability Q as a function of the resonant frequency ωcof the magnetic field at differentelectronphonon coupling strength α.

图9 概率Q在(a)不同介电常数比η和(b)不同磁场的回旋频率ωc下随振荡周期t的变化Fig.9.The probability Q as a function of the period t of oscillation at different(a)dielectric constant ratio η and(b)resonant frequency ωcof the magnetic field.

4 结 论

在计及氢化杂质和厚度效应下,分别选取抛物线型限定势阱和高斯函数型限定势阱描写盘型量子点中电子的横向限定势和纵向限定势,采用Lee-Low-Pines-Pekar变分法研究了电子在磁场作用下的量子跃迁.数值结果表明:高斯函数型限定势比抛物线型限定势更能精准反映量子点中电子真实的限定势;量子点的厚度对电子的跃迁概率的影响不凡;电声耦合强度α、介电常数比η、磁场强度B、非对称高斯函数型限定势阱的阱深V0、阱宽L对电子的能量、声子平均数、能量以及跃迁概率的影响显著.