在兴奋-抑制混沌神经元网络中有序波的自发形成∗

汪芃 李倩昀 黄志精 唐国宁

(广西师范大学物理科学与技术学院,桂林 541004)(2018年3月21日收到;2018年5月22日收到修改稿)

1 引 言

大脑神经系统中包含大量神经元,一个神经元可以与许多神经元同时存在耦合.因此在大脑处理电信号的过程中,神经元集体电活动的时空斑图是极其复杂的.研究发现:在大脑视觉皮层内可以自发出现平行波[1],在睡眠状态下或是药物引起的振荡中,哺乳动物大脑皮层中也会自发出现螺旋波[2,3];此外在癫痫发作时,在大脑皮层中也观察到螺旋波[4].由于螺旋波是一种绕波头旋转的波,因此它可以在介观尺度上组织和调节皮层内神经元的群体活动,从而对大脑的功能产生影响.螺旋波等有序波除了可以出现在脑神经系统外,也可以出现在心脏系统中[5].我们知道心脏是可激发介质,需要起搏源才能使心脏工作.由于螺旋波是不需要波源就能够自维持的波,而心脏中螺旋波的频率通常大于心脏窦房结(心脏的起搏源)产生的靶波频率(即心脏的跳动频率),所以当心脏出现螺旋波电信号时,将引起心动过速,当螺旋波破碎成时空混沌时,就会导致心颤,危及生命.因此,了解大脑神经系统和心脏系统中螺旋波的产生机制及其动力学行为,对了解大脑功能和治疗癫痫疾病、心脏疾病具有重要意义.

最近,人们从理论和实验上对神经元网络中螺旋波的产生机制和动力学行为进行了大量研究[6−12].许多研究结果表明:在神经元网络中,噪声可以诱发螺旋波[7,9,13−15].Qin等[11]在神经元网络中观察到自突触诱发螺旋波和靶波;Ma等[16]发现,增加长程连边概率将导致螺旋波破碎;Wang等[17]发现调节细胞膜上的离子通道电导率也可以导致神经元网络自发产生螺旋波;在近邻耦合Hindmarsh-Rose(HR)神经元阵列中,当神经元处于一周期或二周期态时,如果系统从混沌初相位分布态开始演化,适当选择耦合强度,可以在这样的系统中观察到自发出现螺旋波[18];Fohlmeister等[19]在考虑兴奋耦合、抑制耦合、噪声和轴突延时的情况时,在神经元网络中观察到自发出现螺旋波;Xiao等[20]在由类型I和类型II激发性神经元组成的网络中观察到螺旋波的自发产生;Tao等[21]在由锥体神经元和抑制性中间神经元组成的神经元网络中也观察到螺旋波的自发产生.这些结果表明:噪声作用和与神经元状态相匹配的耦合方式可以使神经元网络自发产生螺旋波,兴奋性神经元与抑制性神经元组合也能导致神经元网络自发产生螺旋波.目前对噪声诱发螺旋波已经研究得比较多,但是对于耦合方式诱发螺旋波的研究相对比较少,需要进一步的研究.

考虑到大脑皮层神经元同时受到大量不相关的兴奋和抑制突触电流的影响[22],在皮层组织培养中,观察到抑制性神经元与总神经元之比达到20%,而在海马组织培养中,观察到抑制性神经元与总神经元之比达到30%[23],因此本文采用HR神经元模型[24]研究混沌神经元网络是否可以自发出现有序波.该网络由近邻兴奋性耦合和长程抑制耦合层组成.我们发现,适当选择两种耦合的耦合强度,系统可以自发产生迷宫斑图、螺旋波、平面波和向内方形波,这些结果对了解大脑中螺旋波和平面波的形成机制具有积极意义.

2 模 型

研究中采用HR神经元模型[24],网络通过在二维方形点阵上增加长程连边形成,其中近邻耦合为兴奋性耦合,长程耦合为抑制性耦合.该网络动力学方程如下:

式中x代表神经元的细胞膜电位;y代表与内电流相关的恢复变量;z代表与钙离子激活的钾离子电流相关的慢变调节电流;a,b,c,d,r,s和x0为HR神经元模型参数;Iext为外部直流激励;D为扩散系数(以下称为兴奋性耦合强度);g为抑制性耦合强度;xth为抑制性耦合的阈值;xav为长程耦合神经元x变量的平均值;m为长程耦合距离;角标i,j=1,2,···,N代表N×N个HR神经元的位置坐标.考虑到实际大脑网络中抑制性神经元占比达到20%—30%,我们每间隔一个格点安排一个抑制性格点,其位置角标为i,j=1,3,5,···,N.在这些格点上,Ωi,j=1,在非抑制性格点上,Ωi,j=0,因此抑制性格点与总格点数之比约为1/4.从(1)—(4)式可以看出,所有格点上的神经元参数相同,但是在抑制性格点上还要考虑长程抑制耦合.

本文固定取a=1.0,b=3.0,c=1.0,d=5.0,r=0.006,s=4.0,x0=−1.6,Iext=3.0,N=201,m=8,xth=−1.5.由于增大m会得到类似结果,因此本文只将D和g设为可调参数,即让这两个参数在0.1≤D≤2.0和0.1≤g≤0.9范围内变化.根据文献[25]的结果,在此参数下单个神经元处于混沌振荡状态.在数值模拟中,解方程采用四阶龙格-库塔法,时间步长取Δt=0.01,近邻扩散耦合使用无流边界条件,抑制性耦合采用周期边界条件,即当抑制格点坐标i′=i−m＜1时,取i′=N+i+1−m,当抑制格点坐标i′=i+m＞N时,取i′=i+m−N−1,每次数值模拟时间长度为10000单位时间.

为了描述系统的振荡状态,引入系统的膜电位方差σ:

当σ小幅度不规则振荡时,系统处于有序振荡状态;σ大幅度无规则振荡时,系统处于混沌振荡状态.

3 数值模拟结果

在给定耦合强度D和g下,系统是否出现螺旋波与系统初态有关.为了比较不同初态的演化效果,我们规定系统初态中各神经元膜电位x＞0的神经元数量与神经元总数之比为ρ.本文通过以下方式产生系统演化的初态:给每一个神经元赋随机初值,然后让神经元在无耦合下演化2000个时间单位.我们发现,继续延长系统演化时间,ρ的值一般在5.5%左右变化.这时我们可以找ρ满足给定值的系统状态作为D和g不为0时系统演化的初态,该初态具有混沌的初相位分布,且系统处于混沌态.在下面的数值模拟中,我只选择ρ=5%与ρ=6%两个初态进行数值模拟研究.

图1给出了不同ρ值下g-D参数平面上的相图,这是系统从两个固定初态演化通过改变耦合强度得到的结果.从图1可以看出:不论ρ取什么值,适当选择兴奋性和抑制性耦合强度,系统都会出现单螺旋波、多螺旋波、迷宫斑图、迷宫斑图与螺旋波共存现象,个别参数出现平面波.在耦合强度相同的情况下,不同的系统初态可能得到不同类型的斑图,但是有如下相同的规律:1)当g=0.1时,系统一般不会出现有序结构,但是在适当的系统初态(如ρ=6%的初态)和兴奋性耦合强度下,系统可以偶尔出现单个螺旋波;2)当g=0.9时,系统很容易出现迷宫斑图、多螺旋波和迷宫斑图与螺旋波共存现象,适当选择兴奋性耦合强度可以出现平面波;3)当g=0.5—0.7时,适当选择兴奋性耦合强度,系统可出现从边界向中心传播的方形波,简称向内方形波;4)在100组参数中,图1(a)和图1(b)分别有21组和22组参数出现迷宫斑图,迷宫斑图出现概率分别为21%和22%,同理可以得到螺旋波(包括多螺旋波)出现概率分别达到29%和26%,只是占据整个空间的大螺旋波(即单螺旋波)出现概率远小于小螺旋波出现概率.向内方形波出现概率分别达到9%和11%,平面波出现概率都为2%.可见在均匀长程抑制耦合下,螺旋波出现概率最大,迷宫斑出现概率次之,平面波出现概率最小.将我们的结果与文献[21]的结果对比可以看出,我们使用相同的兴奋性神经元,引入了抑制耦合,系统就可以自发出现螺旋波,其效果等效在网络系统引入抑制性神经元.这些结果表明,抑制耦合有利于时空斑图的稳定和有序斑图的产生.

考虑到不同初态,系统出现的现象基本相同,下面就ρ=6%情况详细介绍观察到的各种现象.图2给出了不同耦合强度对应的x变量斑图,所有斑图都是从相同初态演化10000个时间单位后的结果,斑图亮度与x变量大小成正比.从图2可以看出,系统可自发出现各种不同有序斑图,有3种不同类型的迷宫斑图,第一种迷宫斑图如图2(b)所示,D=0.1对应的迷宫斑图都属于这类斑图,这类斑图形成过程如下:首先系统自发形成孤子波(图中十字状集团),这些孤子波一开始呈规则分布,而且它们可以自发左右或上下运动,最后排成行和列运动,从而形成迷宫斑图.由于每一个孤子波是可以自由运动,当部分孤子波运动方向发生改变时,孤子波成行运动可以转变为成列运动,如图3所示.当孤子波成行或成列后都朝一个方向运动时,就会形成平面波,如图2(a)所示.当系统同时存在孤子波成行和列运动,且运动方向不变,就会形成图2(c)这种形状的斑图,我们称这种稳定迷宫斑图为第二类迷宫斑图.当孤子波成行和成列后停止运动,就会形成线振源,产生向外传播的平面波,平面波相碰就会消失,这时就会得到不稳定迷宫斑图,如图2(d)所示.如果小的孤子波组成大的振源,迷宫斑图中还会出现靶波,如图2(e)所示.

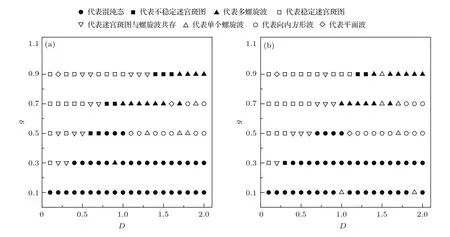
图1 不同ρ值下g-D参数平面上的相图 (a)ρ=5%;(b)ρ=6%Fig.1.Phase diagram in the g-D parameter plane for different values of ρ:(a) ρ =5%;(b) ρ =6%.

图2(f)和图2(g)中显示螺旋波与迷宫斑图共存现象,其产生过程如下:在不稳定迷宫斑图下,小的孤子波成行后以一定概率形成螺旋波,导致螺旋波与迷宫斑图共存现象出现.在本应该出现螺旋

波与迷宫斑图共存的情况下,如果螺旋波的波头形成比较早,螺旋波可将平面波抑制掉,在一些情况下就会出现图2(h)和图2(j)所示的多螺旋波现象.从这些图中可以看出,系统出现了双臂螺旋波(参见图2(h))和螺旋波对(参见图2(j)),螺旋波对产生了靶波.在另一些情况下,系统自发出现单螺旋波,如图2(k)所示.单螺旋波也在系统处于混沌态下自发产生,例如在g=0.1情况下自发出现的螺旋波就属于这种情形.图2(l)显示的斑图为向内方形波斑图,这种波不断从边界产生,然后向中心传播,波形状像口字,因此称为向内方形波.

图2 不同耦合强度下的x变量斑图 (a)g=0.9,D=0.2;(b)g=0.9,D=0.1;(c)g=0.9,D=0.3;(d)g=0.3,D=0.3;(e)g=0.9,D=1.2;(f)g=0.9,D=1.5;(g)g=0.5,D=0.5;(h)g=0.9,D=1.7;(i)g=0.9,D=1.8;(j)g=0.7,D=1.2;(k)g=0.5,D=1.7;(l)g=0.7,D=1.9Fig.2.Pattern of the variable x for different values of coupling strength:(a)g=0.9,D=0.2;(b)g=0.9,D=0.1;(c)g=0.9,D=0.3;(d)g=0.3,D=0.3;(e)g=0.9,D=1.2;(f)g=0.9,D=1.5;(g)g=0.5,D=0.5;(h)g=0.9,D=1.7;(i)g=0.9,D=1.8;(j)g=0.7,D=1.2;(k)g=0.5,D=1.7;(l)g=0.7,D=1.9.

图3 在g=0.9和D=0.1情况下不同时刻的x变量斑图 (a)t=0;(b)t=955;(c)t=9875;(d)t=9905;(e)t=9945;(f)t=10000Fig.3.Pattern of the variable x at different time moments for g=0.9 and D=0.1:(a)t=0;(b)t=955;(c)t=9875;(d)t=9905;(e)t=9945;(f)t=10000.

为了对迷宫斑图和向内方形波演化有直观印象,我们做j=100这一行和i=100这一列格点x变量的时空斑图,图4(a)与图4(c)给出了在图2(c)迷宫斑图参数下对应行与列x变量的时空斑图,图4(b)与图4(d)则是图2(l)向内方形波参数下对应行列x变量的时空斑图.从图2(c)和图4(a)可以看出:图4(a)左边有4个波向右运动,右边也有4个波向左运动,形成粗斜线,因为不同波列对应不同斜线,粗斜线朝右倾斜,波列就朝右运动,如果粗斜线朝左倾斜,波列就朝左运动,如果粗线为水平线,则表示波列不作横向运动.从图2(c)和图4(c)可以看出,图4(c)左边有6个波向上(j增大方向)运动,右边也有4个波向下(j减少方向)运动,形成粗斜线,因为粗斜线朝右倾斜,波列就向上运动,如果粗斜线朝左倾斜,波列就向下运动,如果粗线为水平线,则表示波列不在纵向运动.可见图2(c)迷宫斑图是由朝不同方向运动的平面波形成的.类似由图4(b)和图4(d)可以看出:1)图2(l)是向内方形波斑图,相当在边界上自发形成波源,它产生的波由外至内传播;2)图中反映短暂出现由内向外传播的波,说明中心自发形成的振源产生了向外传播的波,这些波与向内传播的波相遇而消失,因此这种看起来向内传播的波不能称为反靶波,因为传播方向不是指向波源.

图4 不同耦合强度下一行和一列格点的x变量时空斑图 (a)g=0.9,D=0.3;(b)g=0.7,D=1.9;(c)g=0.9,D=0.3;(d)g=0.7,D=1.9Fig.4.Spatiotemporal pattern of the variable x of a row and a column of grid points for different values of coupling strength:(a)g=0.9,D=0.3;(b)g=0.7,D=1.9;(c)g=0.9,D=0.3;(d)g=0.7,D=1.9.

上述结果表明,适当选择耦合强度系统会自发出现有序结构,为了了解系统有序程度,图5给出了不同参数下系统方差随时间的变化,所使用参数与图2对应.从图5可以看出,系统演化初期,系统处于混沌态,系统方差随时间大幅度无规则变化,在系统出现有序结构后,系统方差在某个值附近无规则振荡.这表明整个系统虽然处于有序态,但是单个神经元振荡仍处于不规则振荡状态,表现在单个神经元振荡时峰的数量和振幅在随时间变化,这可以从图2斑图中波臂出现明暗无规则分布可以看出.从图5还可以看出,稳定迷宫斑图和平面波的系统方差变化幅度最小,系统方差变化第二小是螺旋波、多螺旋波和部分不稳定迷宫斑图,系统方差变化第三小是向内方形波和螺旋波与迷宫斑图共存态,混沌态的系统方差变化一般都比较大.对比图2和图5可以看出,系统越有序,其方差随时间变化幅度越小.

上述结果是选择两个初态得到的结果,选择其他不同初态,也得到类似结果,结果表明,出现大螺旋波的概率比出现多螺旋波(或小螺旋波)的概率小,这与文献[15]给出星形胶质细胞合胞体的实验结果一致,实验表明:大螺旋波出现概率小,小螺旋波出现概率大,这表明引入抑制耦合的做法是合理的.

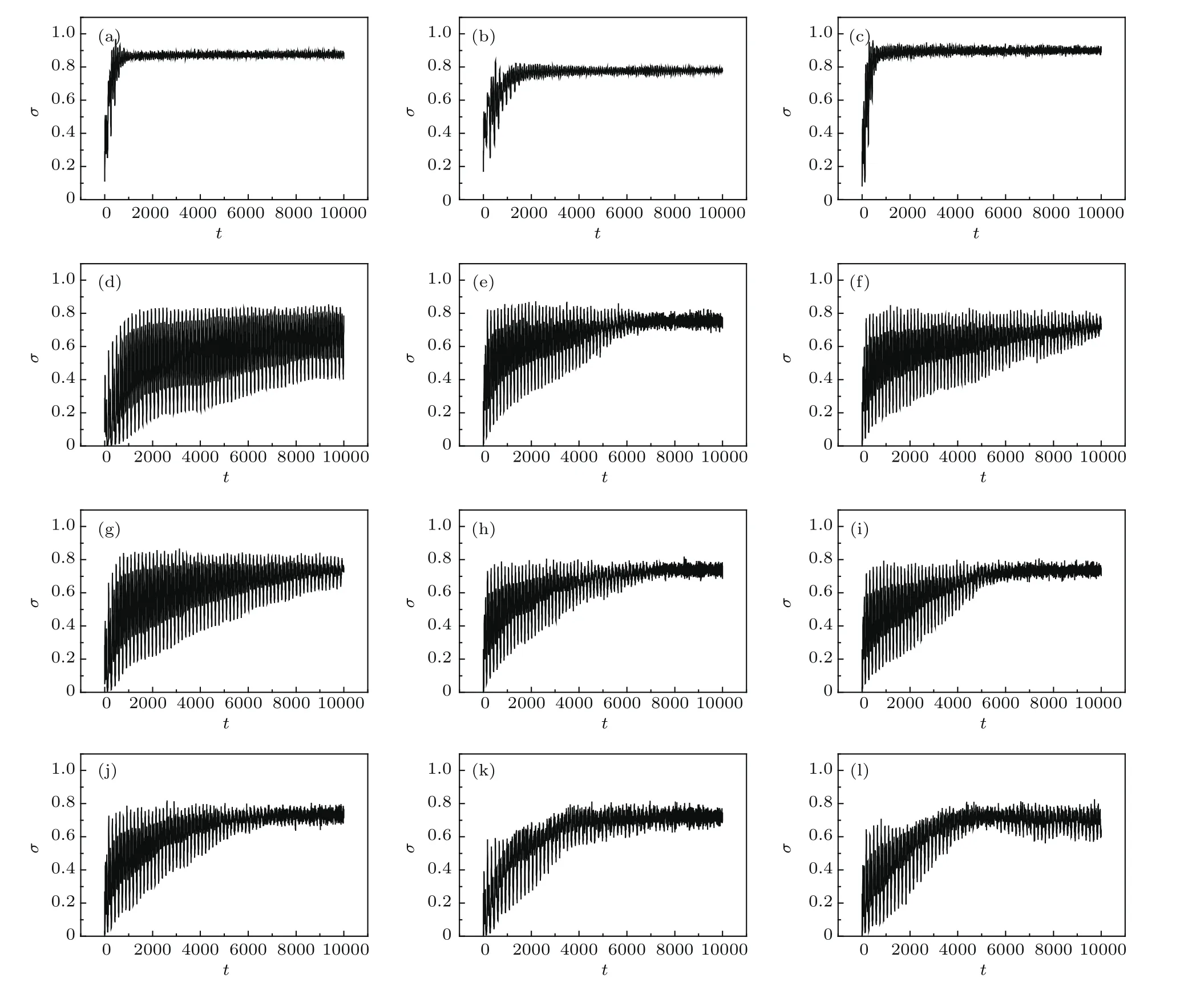
图5 不同耦合强度下系统方差随时间变化 (a)g=0.9,D=0.2;(b)g=0.9,D=0.1;(c)g=0.9,D=0.3;(d)g=0.3,D=0.3;(e)g=0.9,D=1.2;(f)g=0.9,D=1.5;(g)g=0.5,D=0.5;(h)g=0.9,D=1.7;(i)g=0.9,D=1.8;(j)g=0.7,D=1.2;(k)g=0.5,D=1.7;(l)g=0.7,D=1.9Fig.5.Time evolution of the variance of the system for different values of coupling strength:(a)g=0.9,D=0.2;(b)g=0.9,D=0.1;(c)g=0.9,D=0.3;(d)g=0.3,D=0.3;(e)g=0.9,D=1.2;(f)g=0.9,D=1.5;(g)g=0.5,D=0.5;(h)g=0.9,D=1.7;(i)g=0.9,D=1.8;(j)g=0.7,D=1.2;(k)g=0.5,D=1.7;(l)g=0.7,D=1.9.

4 结 论

采用HR神经元模型,研究了在兴奋和抑制耦合共同作用下二维混沌神经元网络系统从随机相位分布的初态演化是否能自发产生螺旋波等有序结构的问题.研究发现,当抑制性耦合强度比较小时,一般系统不会出现有序结构,增加抑制性耦合强度,混沌神经元网络系统很容易产生迷宫斑图和螺旋波.有两种稳定迷宫斑图和一种不稳定迷宫斑图,它们形成的机制略有不同;在给定抑制性耦合强度g＞0.3情况下,逐渐增加兴奋性耦合强度,系统首先出现迷宫斑图,接着系统一般出现螺旋波与迷宫斑图共存态或多螺旋波态,当兴奋性耦合强度足够大时,系统还可出现单螺旋波态和向内方形波态.总之,在适当选择耦合强度下,系统可以自发出现迷宫斑图、单螺旋波、双臂螺旋波、螺旋波对、平面波、靶波和向内方形波等有序结构,迷宫斑图出现概率平均为21.5%,螺旋波出现概率平均为27.5%,向内方形波出现概率平均为10%,平面波出现概率为2%,这说明抑制性耦合有促进混沌系统产生螺旋波和迷宫斑图的作用.

本文研究了由抑制性耦合导致的规则波,采用的是电突触耦合.在大脑神经系统中,神经元还可以通过化学突触耦合和电磁场耦合,研究发现[12]:在电磁辐射作用下,神经元之间能实现同步.因此开展多层网络混合耦合模式放电态的自组织和电磁场辐射对自组织行为的影响研究,有助于人们认识大脑皮层中螺旋波和平面波产生的机制,这也是我们今后要研究的内容,通过这些研究有助于治疗与螺旋波等有序波有关的大脑疾病.