非齐次燃耗方程数值解法∗
2018-09-21付元光1邓力1李刚1
付元光1)2) 邓力1) 李刚1)
1)(北京应用物理与计算数学研究所,北京 100088)2)(中物院高性能数值模拟软件中心,北京 100088)(2017年12月14日收到;2018年4月13日收到修改稿)
1 引 言
核系统运行过程中,核材料不断被辐照,其核素组成随时间发生着复杂变化.在核反应堆物理计算中,通常用燃耗方程来描述核素含量随时间的变化规律:
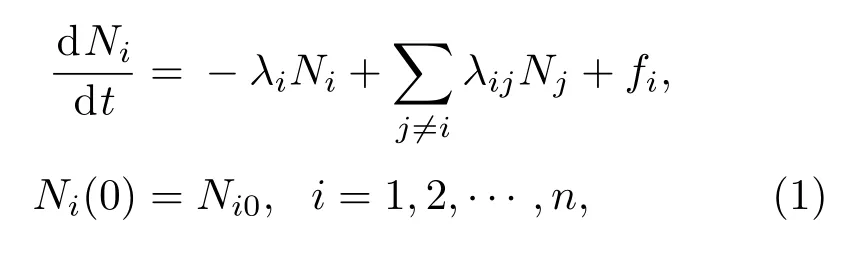
其中n是材料中核素的种类;Ni是第i种核素处于任意时刻t的含量;Ni0是第i种核素初始时刻的含量;λij是第j种核素反应(包括中子诱发、衰变等)产生第i种核素的转换系数;λi是第i种核素发生反应(包括中子诱发、衰变等)的消亡系数;fi是第i种核素的迁移率.燃耗方程也可写成矩阵-向量形式

其中N是n维核素含量向量,N0是N在t=0时刻的值,A是由系数λij和λi构成的n×n维燃耗矩阵.在实际问题中,燃耗方程包含数百至上千种核素,核素之间存在复杂的转换关系,严格来讲,描述核素产生、消亡的系数λij和λi是随时间变化的,但变化比较缓慢,在适当的时间步长内,可将λij和λi视为常量,使燃耗方程成为一阶线性常微分方程组,再通过数值方法进一步求解.
求解燃耗方程有两大技术路线,其一是线性子链方法(TTA)[1−3],通过解耦核素之间的转换关系,生成一系列线性子链,再根据常微分方程理论逐一解析求解每条链;线性子链算法精度高,但链的构造过程十分耗时,同时为保证算法稳定性,需要更费时的高精度浮点计算支持;其二是矩阵方法,通过数值方法求解矩阵tA的指数etA,主要有泰勒展开法[4]、Krylov子空间法[5]、切比雪夫有理近似法 (CRAM)[6−8]、Padé近似法[9]等,矩阵方法求解速度快很多,部分方法与TTA精度相当.目前,大部分燃耗数值计算程序主要借助以上算法求解齐次燃耗方程问题[10],即在(1)式中令fi=0,这是由于在常见的核反应堆中,不同空间区域之间核素迁移不显著,燃耗区相对独立,求解齐次方程已能够满足精度.对于一些新型核能系统(如熔盐堆、液态散裂靶等),具有显著的核素迁移,必须求解非齐次燃耗方程.在众多程序中,ORIGEN[4]和CINDER90[11]是两款可以求解非齐次燃耗方程的程序,但仅能处理fi为常量的情况,这种情况已能够满足大部分实际应用需求.对于CINDER90,虽然能给出正确解,但计算耗时很长;对于ORIGEN,如果指定fi<0,可能导致结果发散.
本文研究了非齐次项fi具有特殊含时形式时方程的解法,在若干已有程序只能计算fi为常量的基础上,扩展了fi适用范围.设fi能够在t=0附近(t=t0类似,只需要一个平移变换)通过有限阶泰勒展开有效逼近,即
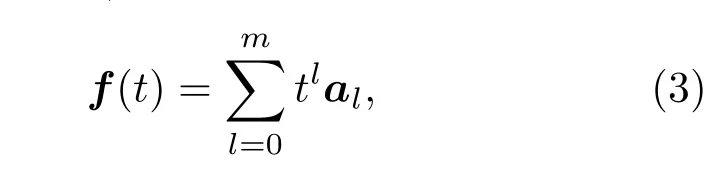
其中al是展开项向量,则非齐次燃耗方程变为
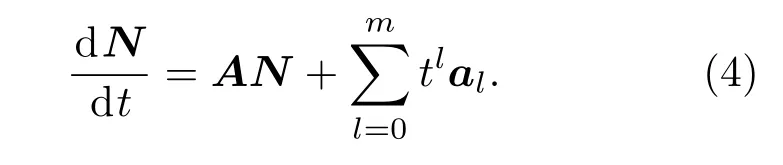
基于方程(4)的形式,本文使用了两种求解方法:首先推导出了基于TTA方法的解析解形式,然后计算了基于矩阵方法的矩阵级数解的近最佳有理逼近表达式,通过不同方法的计算结果比对,验证了两种方法求解特定形式非齐次燃耗方程的可行性.
2 理论推导
2.1 非齐次燃耗方程基于TTA方法的解
TTA方法的基本思想是将核素之间的复杂转换关系解耦成若干线性链,在一条线性链上,一个核素只能经由一个母核反应生成,且该核素发生反应只能生成一个子核,只有链首核素具有迁移率和初始核子密度,其余核素都为0.这种简单的传递关系和初始条件使得描述一条线性子链的微分方程组可解析求解.逐一求解每一条线性子链,再把每条链的贡献累加即得到结果.描述一条线性子链的微分方程组为
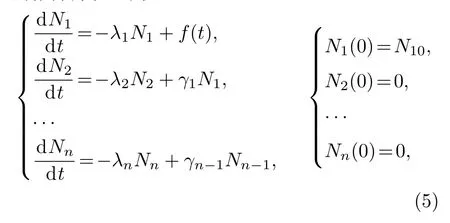
其中n是链包含的核素数目;Ni是链上第i个核素在任意t时刻的含量;γi是第i个核素生成第i+1个核素的转换系数(γi≤λi).若(5)式中非齐次项满足则方程组中第一个方程的非齐次项变成m+1项之和,根据线性常微分方程理论[12],方程组的解为1个齐次方程组的通解和另m+1个非齐次方程组的特解之和,第l个非齐次方程的非齐次项正是tlal.若通解为Nbase,特解分别为N(l)(l=0,···,m),则方程组的解为对第l个非齐次方程组进行Laplace变换,设变换后的向量为n(l)(p),其第K个分量满足

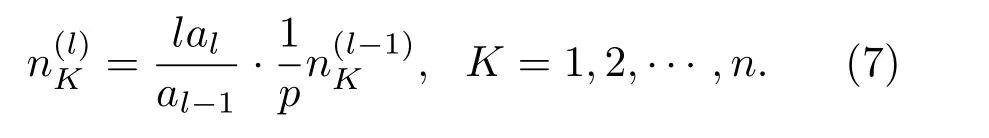
再对(7)式进行Laplace逆变换,可得如下递推关系:

(8)式说明第l个和第l−1个非齐次方程组的解存在递推关系.综合上述推导得到解方程组的流程:
1)求解齐次方程组,先对方程组的第一个方程Laplace变换,得到第一个变换分量,并利用递推关系(6)式得到所有变换分量,再对所有变换分量进行Laplace逆变换,得到Nbase;
2)求解非齐次方程组,先解l=0的方程组,类似1)的流程,得到N(0),根据递推关系(8)式,再对N(0)进行多次积分,可算出全部N(l);
3)将以上所有解相加,得到最终解.
经过一系列推导,可得到解的普通形式,它给出了一条线性链上任意一个核素在任意t>0时刻的含量:

在以上推导中做了λi/=λj的假设,现实情况中,线性链上可能存在多对相同的核素,使链出现局部闭环,导致假设不满足.为防止计算式发散,必须进行处理.一种方式是考虑λi=λj的情况运用极限进行重新推导,得到一组新的解析表达式[2];另一种方式是对相等的λi做微小的扰动Δλ,人为确保λi互不相等.有研究表明[13],前者对计算精度略有提升,但会额外引入计算量,后者对计算精度影响不大.本文选择相对更容易实现的后者.
2.2 非齐次燃耗方程基于有理近似方法的求解
有理近似方法的基本思想是用一个有理分式在rk(x)某个区域上逼近目标函数f(x),如

其中Pk,Qk是k阶实多项式,无公因子,一般情况下令Qk常数项为1.(10)式也可以写成如下形式:

矩阵函数同样可以用关于矩阵的有理分式逼近,根据矩阵函数的定义可以将(11)式推广到矩阵[15],即

其中I是单位矩阵.如果k是偶数,则{θi},{αi}分别是k/2个共轭数对,(12)式的运算可以减半,变为
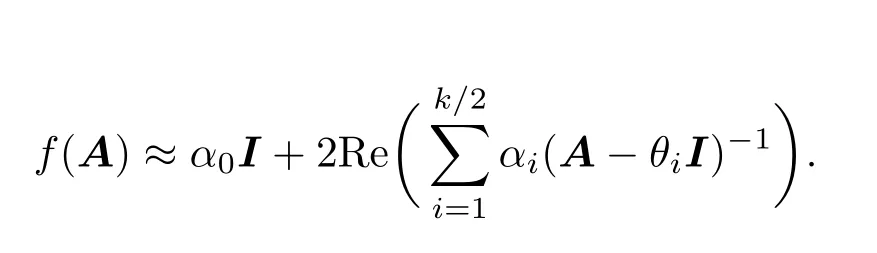
对于燃耗方程(4)式,若方程的初始条件为N(0)=N0,将其代入如下递推式:

可求出N1,再用N1求出N2,一直进行下去,直到m→∞,得矩阵级数形式的解[16]

在实际燃耗问题中,有些核素的衰变非常快,致使消亡系数很大,有些问题中时间步长t也会取很大,使得‖tA‖>1020,直接求解矩阵tA的上述级数展开不可承受.如果找到相应的有理逼近式,就能避开直接求解的困难.定义和函数Hl(x)满足:如能找到Hl(x)的有理逼近式,根据(12)式,可将级数求和转换成有限项计算:



图1 Δ(t)=Hl−r14的图像 (a)H−1的Δ(t);(b)H0的Δ(t);(c)H1的Δ(t);(d)H2的Δ(t)Fig.1.Curves of Δ(t)=Hl−r14:(a)Δ(t)of H−1;(b)Δ(t)of H0;(c)Δ(t)of H1;(d)Δ(t)of H2.
实函数一般具有惟一的最佳有理逼近[14],称为最佳Chebyshev有理逼近,寻找方法主要有Remez方法[17],Carathéodory-Fejér方法[18−20](CF方法)等.Remez方法的基本思路是在区间[−1,1]上选定2k+2个Chebyshev多项式零点{cn},n=1,···,2k+2, 在这些点上 目标函数和有理逼近式的残差以δ水平交替变换,即由于Pk有k+1个未知系数,Qk有k个,连同δ,共2k+2个未知数,正好和方程数相等,于是可求出所有系数和δ,如果δ过大则需要调整{cn}的位置,并继续求解方程,直至δ收敛到期望水平.Remez方法是一种迭代过程,需要求解非线性方程组,计算量大,难收敛.CF方法的基本思路是在区间[−1,1]上用Chebyshev多项式展开目标函数,用展开系数构造Hankel矩阵,Carathéodory-Fejér定理具体给出了目标函数和最佳有理逼近式的残差的具体形式,它可以用Hankel矩阵的特征值和特征向量表示,进而通过残差求出最佳有理逼近式.事实上,CF方法求出的仅是最佳逼近式的一个近似逼近,由于近似逼近向最佳逼近的收敛速度很快,可认为二者基本等效[14].CF方法的实现流程较为复杂,但不需要迭代,数值稳定性好.CF方法一般在[−1,1]区间上求解目标函数的最佳有理逼近式,对于燃耗矩阵tA,有研究表明[6]一般情况下其特征值分布在复平面负x轴上或附近,因而需要得到目标函数在(−∞,0)上的近似式,用以计算tA的矩阵函数,为此可进行变换x=进而对目标函数使用CF方法,再代回x即求出目标函数f(x)在(−∞,0)上的最佳逼近式.

表1 Hl(x)的14阶有理逼近式系数Table 1.Rational approximation coefficients of order 14 of Hl(x).
本工作借鉴文献[18]所述流程,用C语言和高精度浮点计算库第三方库实现了CF方法.目前只计算了Hl(x)在l=−1,0,1,2情况下的最佳有理逼近式,每个和函数的逼近阶数k从2算到20.最佳有理逼近的精度按O(9.29−k)收敛[18],k取值过小无法保证精度,过大则增加计算量,k取14是相对折中的做法.表1列出了k=14时,Hl(x)对应的最佳有理逼近系数,取11位有效数字(实际计算中算到了30位有效数字);图1是和14阶最佳有理逼近式在t∈[−1,1]内的绝对误差Δ(t)的图像,可看出误差以α0水平振荡;图2是Hl(x)与最佳逼近式最大误差随逼近阶数k的变化情况,可看出当l越大,误差越小,说明越大的l对应的Hl(x)越容易收敛.
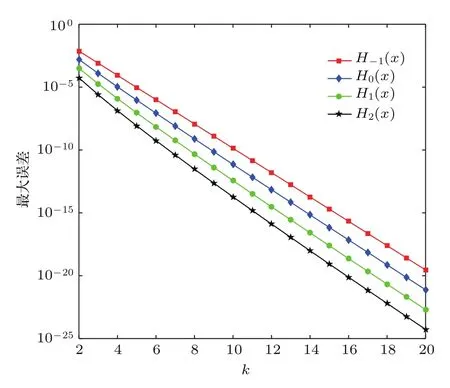
图2 Hl-rk最大绝对误差随k的变化情况Fig.2.Maximum absolute error of Hl-rkvarying with order k.
2.3 方法适用范围
以上方法都是基于非齐次项满足f(t)=推导出的,在许多情况下,非齐次项需要用非常高阶的泰勒展开逼近,甚至不能被有限阶泰勒展开很好地逼近,这时使用上述方法计算量非常大,可能还会失效.不过,以上方法的推导过程为更一般情况的处理提供了一种思路,沿用上述方法流程,有可能求解非齐次项f(t)为其他形式时的情况.
对于有理近似方法,可以先寻找和燃耗方程(2)具有相同形式的代数方程y′=−λy+f(t)的一个特解h(t),只要h(t)在问题所关心的t范围内有界、无奇异,对于任意t能明确给出h(t)的值,无论h(t)是何种形式,即便h(t)可能存在不可积的情形,都可以通过CF方法求出h(t)的一个最佳有理逼近式,从这一点讲有理近似方法的通用性比TTA方法要好.但需要说明,对于不同h(t),达到期望的逼近精度所需要的有理逼近式阶数也不同,有些h(t)需要非常高的逼近阶数,这会增大计算量.本文求出了f(t)=tl,l=0,1,···,m情形下的h(t),用14阶逼近就可以达到很高的逼近精度,但对其他形式的f(t)未必够用.
本文只从操作实现上论述方程求解的可能性,对于更多形式的f(t)是否可解,限于作者水平无法系统展开.对一些实际工程问题,如液态散裂靶的运行,由于束流轰击散裂靶的强度随时间变化并不剧烈,散裂产物的累积速率相对恒定,可近似认为非齐次项为常数项,本文所述方法能够胜任求解.
3 数值实验

将以上算法集成到了北京应用物理与计算数学研究所开发的燃耗计算程序JBURN中,通过两个数值算例验证程序功能的正确性.首先是一个小型矩阵问题,矩阵规模为6×6,非齐次项展开到2阶.各系数和初始条件详细如下:其中A的特征值全为负,最大特征值和最小特征值差距11个量级,且A能够对角化. 计算t=105,106,107时刻的解,此情况下tA的范数约为109—1011.若A的特征值对角阵和特征向量阵为Λ和P,即A=PΛP−1,代入(15)式易得Hl(tA)=PHl(tΛ)P−1,根据矩阵函数定义[15],Hl(tΛ)也是对角阵,它的每个元素可由tΛ的每个元素代入Hl(x)中直接求出,以这种方法得到的结果作为基准,分别使用TTA和有理近似方法求解,结果列于表2.可以看出,两种数值解法与参考解所得结果相差很小,有些完全一致,验证了方法的正确性.
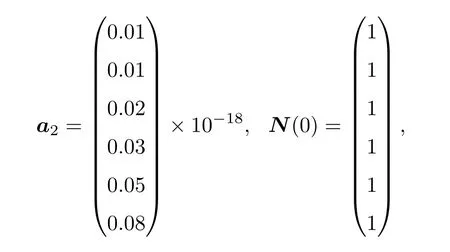
第二个算例基于真实的核素反应数据库,计算MOX核材料经5.3075×1015cm−2·s−1大小的中子通量密度辐照20天后各种核素的含量,材料的具体成分和各种展开系数列于表3,其中正展开系数表示核素不断地由外界补给,负展开系数表示核素向外界流出.

表2 小型矩阵问题在不同时刻的解Table 2.Solution of small matrix problem at different time.

表3 MOX燃耗算例计算初始条件Table 3.Initial conditions of MOX burnup example.
核反应数据库中包含3400种核素,因此矩阵A的规模为3400×3400,tA的范数约为1030.用数值方法求解tA的特征值和特征向量耗时且不稳定,因此无法像算例一一样给出参考解,仅给出TTA方法和有理近似方法的计算结果,其中核素含量小于10−24时强制设为0.图3给出了3400种核素的计算结果,并给出计算相对偏差,从图中可以看出,绝大部分核素含量的计算结果符合得很好,偏差小于10%.进一步统计,3400种核素中有1251种核素含量不为0,其中26个核素的偏差大于10%.303个核素偏差在0.1%—10%之间,481个核素偏差在10−3%—0.1%之间,441个核素的偏差小于10−3%.表4列出了工程计算中几种重要重金属和裂变产物核素的含量对比情况,可以看出,对于重核而言,计算偏差非常小,偏差最大的243Am也只有5.91×10−2%;对于裂变产物而言偏差稍大,但偏差最大的151Sm也不超过1%,说明两种方法的精度足够满足工程应用需求.
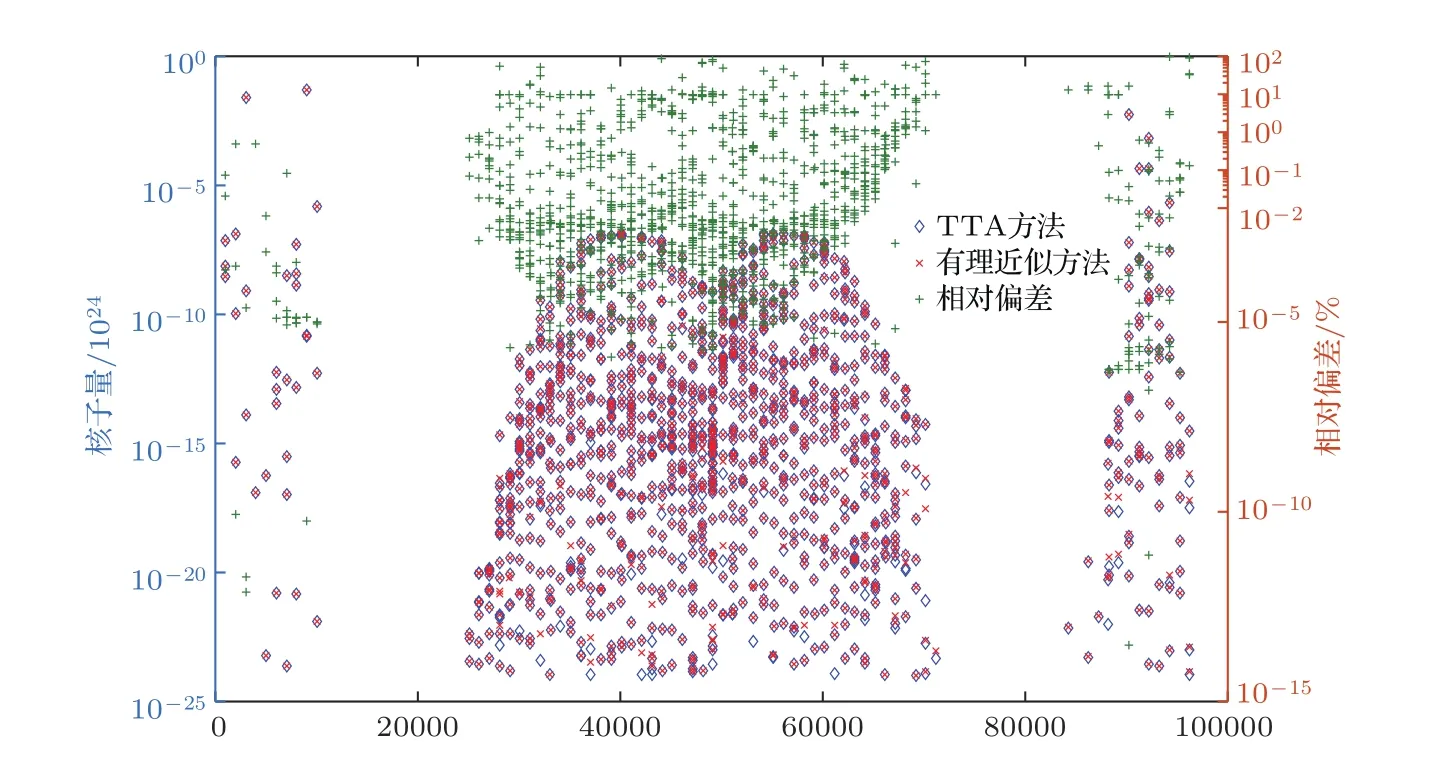
图3 两种方法计算MOX材料燃耗结果与相对偏差Fig.3.Results and relative error of MOX burnup calculated by two methods.

表4 重要重金属与裂变产物核素含量Table 4.Quantity of important actinides and fission products.
在计算耗时方面,TTA方法耗时约85 s,有理近似方法仅耗时0.8 s,显著快于TTA方法,主要原因是TTA方法需要通过回溯算法搜索构造线性子链,本问题中构造出300多万条核素链,成为最耗时的因素.一般而言,对于考虑重金属裂变的问题,线性子链个数会相当庞大,TTA方法耗时会显著高于有理近似方法;对于纯粹的核素衰变问题,只需要若干个线性子链就能描述,这时TTA方法则会显著快于有理近似方法.有理近似方法耗时主要在解线性方程环节,根据(12)式,方程的个数和有理逼近式阶数成正比,对不同问题,在相同逼近阶数下,有理近似方法求解速度没有显著波动.
4 结 论
本文初步研究了非齐次燃耗方程的两种数值解法,用以求解方程非齐次项含时的情况.在非齐次项能够被有限阶泰勒展开逼近的条件下,首先基于Laplace变换推导出了方程基于线性子链方法的解析表达式,然后使用CF方法计算了矩阵级数解的近最佳有理逼近式.使用不同方法计算两个数值算例,结果符合很好,验证了方法的正确性与精度.本文的方法在计算精度和效率上能够满足工程计算要求.方法的实现流程也为非齐次燃耗方程的求解提供了一种思路,在后续工作中,可借鉴上述方法,求解含有其他形式非齐次项的燃耗方程.
