面向线性文本的K-means聚类算法研究

文必龙，李 菲，马 强

(东北石油大学 计算机与信息技术学院，黑龙江 大庆 163318)

0 引 言

一篇具有明确主旨的文章，多采用一定的组织形式去组织文本内容。从文本内容中挖掘有用信息，是目前文本挖掘、文本信息抽取等相关领域研究的重点[1]。作为一种能将不同组织形式的文本根据内容聚集成簇的关键技术，聚类技术为文本内容的进一步分析挖掘提供了有力的支撑。K-means算法是基于划分思想的经典聚类算法[2]，是一种采取随机确定初始点作为中心点，然后不断循环迭代求得最大相似性的类别划分算法[3]。该聚类算法针对主题掺杂、内容组织无序的文本，具有简单、收敛速度快、处理大数据文本集有效等优点[4]。传统K-means算法随机初始化中心点，在迭代聚类时会有以下问题：需要输入最终结果的聚类个数k[5],而判断一个未知数据集的划分个数通常是很困难的；k个初始点的选择对最终的聚类结果影响很大[6]；聚类过程中的迭代总次数增加使得聚类过程中的总耗时增加[7]。为解决以上问题，文献[8]从样本几何结构角度，设计一种新的聚类有效性指标，依此确定最佳聚类数。文献[4]和文献[9]在初始化中心点上分别采用最大距离积法、密度区域相距最远来确定初始化中心点。文献[10]和文献[11]分别提出了基于最近高密度点间的垂直中心点优化初始聚类中心和基于密度峰值优化的K-means文本聚类算法，解决了聚类效率低和局部最优解等问题。在对整篇文章的内容和组织结构进行分析时，发现文本具有基于某一主题下的有序组织的线性文本，对其采用传统的K-means算法会存在以下问题：(1)篇章主题内容划分的随意性较大。在不考虑线性文本具有的上下文内容划分的清晰界限，采取文本段落向量的相似性进行聚集分类时，聚类主题的侧移影响最终结果；(2)随机初始中心点的方式增大了聚类初始点的不确定性，在选择不当的情况下使得迭代次数增加或无穷迭代、延长运算时间等。同时，该算法在处理段落文本到各个中心点的距离相等时，归类不当也会造成聚类结果的不精确等问题。

针对以上问题，文中深入分析线性文本内容的组织特性，提出一种随机均匀初始化中心点的K-means文本聚类算法，主要用来解决线性文本自身段落内容、层次、主题等的聚类问题。同时改进收敛函数，提出等距点归类法以解决特殊段落到中心点距离相同时无法准确归类的问题。

1 线性文本

1.1 定 义

线性文本指的是阅读时有先后顺序，基于一个共同主题下划分各个相关子主题，子主题之间相互独立、均匀分散、段落在组织上具有线性结构的一类文本。传统的教材课文不管文字排列的方式如何，文章的写作和学习者的知识学习都要依靠一种相继的线性顺序进行，段落和章句之间必然依照逻辑、衔接和顺序来联结成一体，这是线性文本的特点。

线性文本具有较强的思维逻辑性和层次结构性[12]。与非线性文本相比，避免了让读者在阅读中肆意游荡。非线性文本中的各子主题[13]内容之间相互融合掺杂，文本段落在组织上杂乱无序、胡乱堆砌、毫无界限和标志之分(结构见图1(a))。在采用传统的K-means文本聚类分析时，随机初始化中心点可保证杂乱主题被任意选取到，但是因为不确定性的存在，会使得聚类迭代次数增加或无穷迭代、文本中心意义的曲解和偏差等。线性文本从始至终是基于一个主题的，主题一般以抽象概括的语言显性或隐性地存在于整篇的篇章当中[14]，并且以主题为轴心做逻辑导向划分子主题，实现文本内容的层次划分。表现层次的完整的单位是段落，文本最终形成一棵文本的结构树[15](结构见图1(b))。文中把线性文本的逻辑结构表示为：文本={文本主题，层次主题，段落主题，句子，主题词}。

图1 线性与非线性文本对比

在对线性文本进行结构分析时，其有序化的组织特性，决定了K-means聚类分析的有序性。文中基于一篇线性文本，对其内容进行K-means划分。具体定义如下：设文本d具有个n自然段，k个子主题(也是k个内容层次，认为内容层次是依据子主题进行的划分)，用H表示划分的文本内容，P表示自然段。

定义1：待分析文本d。

d={P1,P2,…,Pn}

定义2：文本聚类分析后的内容划分[14]。

d={H1,H2,…,Hk}={Pi1…Pi2-1}{Pi2…Pi3-1}…{Pik…Pik+1-1}

其中，i1=1≤i2-1≤…≤ik≤ik+1-1=n(为方便以后表示，d=P1,P2,…,Pn简记为1,2,…,n)。

而在文本逻辑结构中更加强调的是文本所包含的思想内容(内容划分)，段落单元是该段落的中心思想，作为文本结构树的叶子节点，段落间在表现主题时用词上会存在差异，也就支撑了段落中心思想的聚集程度。线性文本的有序聚类就是寻找一种分法使k个内容层次内的差异尽可能小，而层次间的差异尽可能大。

1.2 线性文本的空间向量模型

为了让计算机能对文本进行操作，采用向量空间模型(VSM)对文本进行表示[16-17]。其基本思想是：将文本中不同的词语(一个词语是一个维度)，按照它们的重要程度，赋予不同权重[17]。最后文档集合D中的任一文本dk都表示成向量形式：dk=(Wk1,Wk2,…,Wkh)，其中Wkg是文本dk中第g个词语的权重，h是D的维度，也称文本向量的基数[18]。那么，针对线性文本有：

定义3：设文本d的特征项集为T={t1,t2,…,tm}(为了方便表示，亦可记为1，2，…，m)。则设Pi={Wi1,Wi2,…,Wim}为第i段的特征向量[19]。其中Wiq是特征项tq(q∈[1,m])在第i段中的权重，特征项计算的是词语的权重，形成如下文本空间矩阵[11]：

在该模型中，使用TF-IDF作为特征词权重的度量[16-17]。

Wkq=TFq×log(N/DFq)

(1)

计算TF(term frequency)，有不同的归一化方式：

(2)

(3)

其中，sum(doc_length)为文本总词频；max(tfd)为文本d中的最大词频，文中选用的是单个段落的总词频；n为自然段落总数；DFq为包含词语q的段落总数目。

1.3 K-means聚类算法的不足

K-means是一种基于迭代思想的聚类算法，从v篇预处理的文本集合D={d1,d2,…,dv}中选取k个初始簇中心，并依据相似程度将文本划分到最相似的簇中，最终形成k个簇的集合C={c1,c2,…,ck}。具体算法的实现步骤如下[20]：

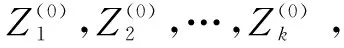
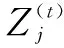
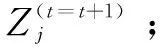
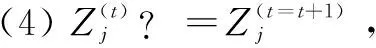
(5)输出最终簇集合C*。

传统的K-means算法在处理线性文本时，采取随机挑选中心点并不断迭代的聚类方式，中心点的不确定性较大，在选择不当的情况下造成迭代次数增加、运算时间加长[21]。例如：初始化中心点时，在本属于同一簇的文本中选取多个中心点，以及忽略线性文本具有的上下文内容划分的清晰界限，在中心点选取上不均匀，使得聚类中心主题的偏移，影响聚类最终结果；同一个文本到多个中心点距离相等以及孤立点时，会干扰文本的聚类效果，最终无法准确归类(见表1)。因此，急需改进中心点选取算法及处理等距点现象的归类方式。

表1 文本到中心点距离对比

2 随机均匀初始化中心算法

针对线性文本特性采取均匀初始化中心点的方式，可以精确地确定主题范围。因为线性文本的段落表意明确、集中，含有丰富的语义，在篇章当中段落间会存在并列、顺承等一些线性特征，也就使得表现主题内容的各子主题之间线性排列。

具体采用的随机均匀初始点算法(如图2所示)如下：

设具有n个自然段的文章d={P1,P2,…,Pn}，P表示段落，共有n个自然段落，聚类数目为k。

为使聚类结果有意义(过大或过小的k值都会影响聚类结果)，在选定k值时，默认取值范围是[Kmin,Kmax]，其中Kmin=2，Kmax=sqrt(n)[22]。

一篇线性文本W可划分成具有k个子主题的簇集C，k个主题的内容在段落形式上呈线性排列，则选取初始化中心点也呈线性排列。其中，段落均匀间隔为dis=(n/k)。

(1)为了保证随机选取的中心点有意义，随机选择的第一个中心点为Px(x∈[1,dis])。

(2)根据Px及dis获取其他中心点p=Px+r*dis(r∈[1,k-1])。

(3)形成初始点簇成员集Cstart={Px,p}。

图2 随机均匀初始化中心点

文本中，各子主题间为了突出各自内容，相互之间相似程度较小，从而在整篇文章上呈现主题间的并列或递进等线性排列特征。同时为避免文章冗余，主题内容的规模分布上多呈现出均匀分布特性。根据这种均匀特性，采用随机均匀初始中心点，可以更好地保证初始点间的相似度小。并且，该算法可使中心点均匀地分布到各个子主题内容中，避免随机性太大造成的初始点过于集中与分散的情况，有利于相似内容最快归类，提高聚类效果与速度。

3 等距点归类法

通过前面的模型，得到随机均匀选取初始点的K-means算法，但该算法在迭代时需要解决文本段落归类的问题。实验中发现，由于篇章内容少这个特性，使得对段落聚类时，每个段落向量有可能与其他内容都不相似或与多个簇的中心相似度相等，将这样的段落称为“等距点”，等距点可能即使多次迭代，仍不能将其划分到相近的类中。为解决该问题，提出如下归类处理方法。

定义4：簇的平均值。

(4)

其中，h为文本内容层次，ih属于文本内容h的一个自然段落。

该公式用于计算任意簇中所有自然段落空间向量坐标的平均值，计算结果作为簇更新后的中心点。

定义5：最大迭代次数max=ε。

(1)计算非中心点pi(i≤(n-k))到簇集Cstart即(Cstart,pi)之间的相似度sim(pi,Cstart)，选取最大相似度的簇对sim(pi,Cz)(z∈{1,2,…,k})，将pi,Cz合并成新簇，Cnew=pi∪Cz；当段落到多个中心点距离相等时，默认先不进行归簇(增加一次迭代)。

定义6：计算任意两个段落之间的相似度-夹角余弦距离[19,23]。

sim(pi,pe(pe∈Cstart))=

(5)

(2)计算新簇的平均值mean(Cnew)，从而构成Cnew={Cnew1,Cnew2,…,Ck}。

(3)判断Cnew?=Cstart，若相等或者t=ε，执行步骤4，否则，进行赋值：Cstart=Cnew，t=t+1。然后跳转到步骤1。

(4)判断d={p1,p2,…,pn}都合并，未合并的，将其单独并为一类Ck+1。

(5)输出聚类结果。

4 实验结果分析

将改进的K-means算法聚类结果进行评价研究的过程称为聚类有效性分析(cluster validity)。聚类有效性分析一般分为外部标准评价和内部标准评价[24]。外部标准评价(external criteria appraisal)，用于标定的聚类结果集，采用相应的评价指标来评价聚类质量。内部标准评价(internal criteria appraisal)，直接评价聚类算法的目标函数值，由该标准衍生出来的评价指标称为基于目标函数的指标[24]。

为验证该算法的有效性，以《人民日报》语料中的整篇文档作为实验文本，选取7个类别共8篇，每篇的段落数如表2所示：

基于内部标准评价，采用类内类间相似性度量函数[25]，对聚类质量进行评判。

具体计算公式如下：

(6)

其中，d(Xi,Xj)为文本之间的余弦相似值。该值越大，文本的相似性越高，反之，相似性越低。

实验结果如表3所示。

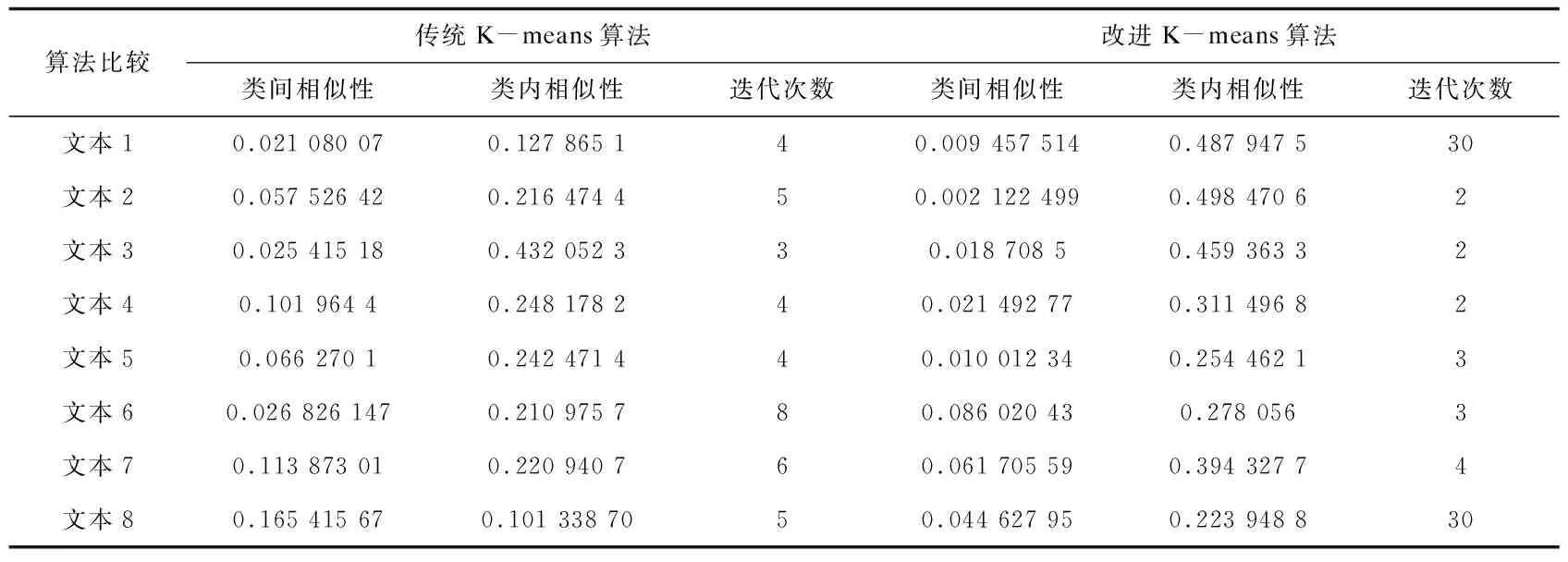
表3 聚类实验效果

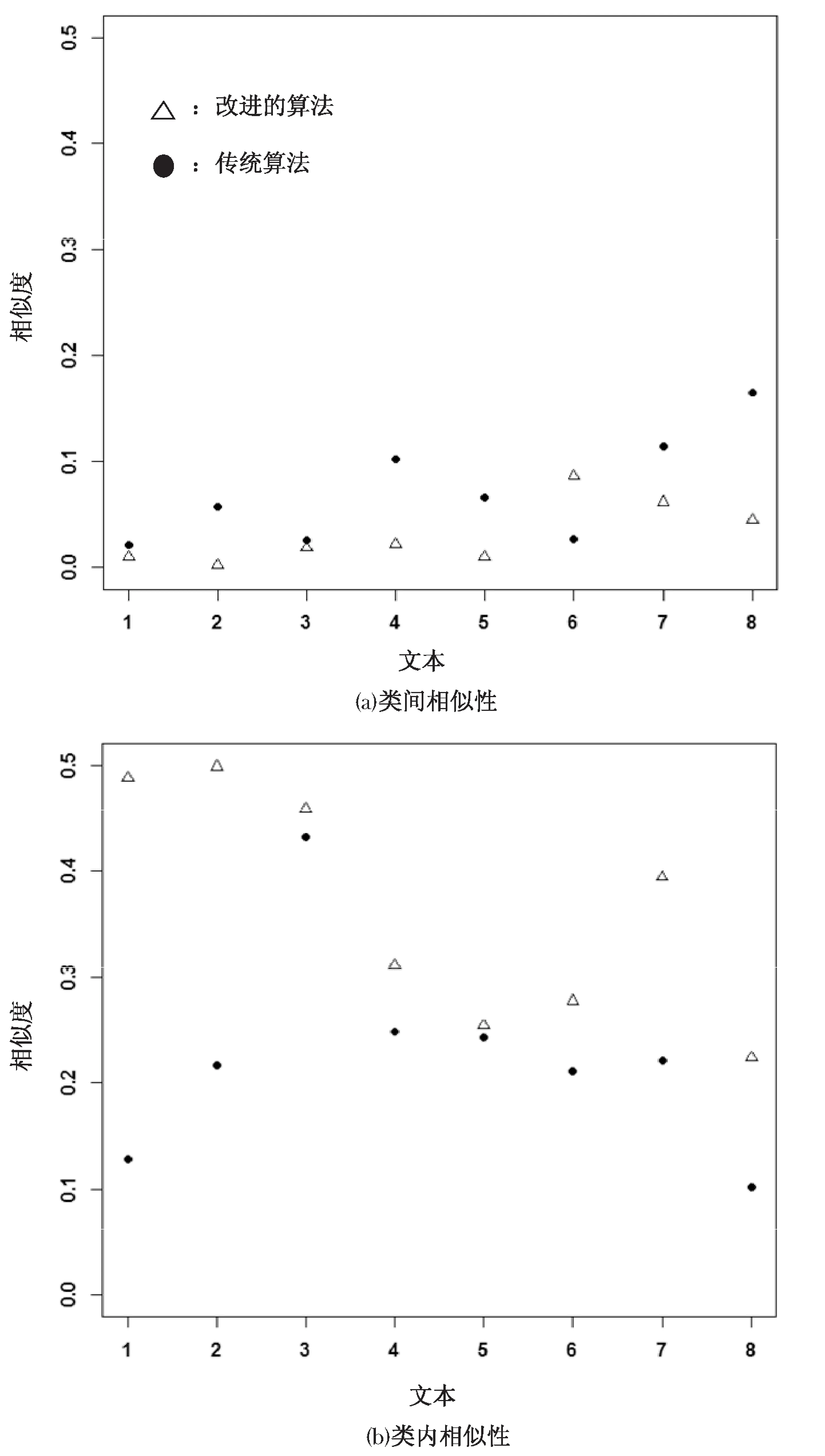
图3 相似度对比

由表3可以看出，当未出现孤立点及文本段落到多个中心点距离相等时，改进算法降低了聚类迭代次数，缩短了聚类时间。相反的情况下，采取最大迭代限制并进行优化归类，提高了聚类结果的准确度。如图3的实验结果可以看出，传统K-means聚类算法类间相似度大于改进之后的算法结果，说明传统算法在簇间区分上不如文中算法的簇间区分性好，并且改进算法很大程度上降低了文本的耦合性[26]；在类内相似性上，传统算法类内相似性小于改进之后的计算结果，说明簇内文本之间的紧凑程度要劣于文中算法。

5 结束语

针对组织有顺序的线性文本，考虑文本结构化特性，对传统K-means聚类算法在内容聚类上的不足进行改进，提出一种新的中心点确定方法—随机均匀选点；基于文本分布和迭代次数的等距点归类方法，构造了一种基于线性特征的自动文本内容分析算法，对深入理解文本、挖掘文本中的主题和有用信息，具有重要的意义。实验结果表明，该算法提高了线性文本的聚类效率，在形成以子主题为中心的簇集分类上优于传统的K-means聚类算法。下一步将在此基础上，依据文本的语义特性、相似度等特征自动确定k值，以期达到更好的聚类效果。