复杂环境下结构光中心线提取算法

杨镇豪，杨 柳，李 辉，陈建政

(1.四川大学 计算机学院，四川 成都 610064； 2.西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引 言

在三维测量(three-dimensional measurement)图像处理系统中，线结构光测量技术是一种应用广泛、测量有效的光学测量方法，其原理是线光源激光器产生的光束投射到待测工件表面，用CCD相机拍摄调制后的激光光带图像，然后根据光带中心位置的偏移计算出测量物体的三维信息。

由于测量系统中的激光光束质量、测量环境和待测物体表面的光学性质都会对摄像机采集到的光带图像造成影响，从而对中心线的提取带来各种问题，所以如何精确快速地提取图像中线结构光光带中心线，是整个测量系统测量精度的关键。多年来，国内外学者就此问题提出了多种方法，比较常见的主要有极值法、几何中心法、灰度重心法和Steger法等[1-2]。极值法与几何中心法通过寻找图像灰度值的极值与几何中心计算光带中心线，原理简单，运算速度较快，但是精度只能达到像素级别，难以满足工业测量的要求。灰度重心法利用激光光带能量类似高斯分布的特性计算光带中心，稳定性优于极值法，但其准确性易受图像高频噪声和光带非正态分布的影响，仅适用于图像光带质量较好的场合[3-4]。Steger法利用Hessian矩阵获取激光光带像素点的法线方向，通过法线方向上的极值点计算出亚像素光带中心线，精度高，但是对光带宽度敏感，且运算量大[5-8]。

实际工程应用中，一般使用的激光器是普通的激光器，投射出来的光带质量稳定性、均匀性不高，此外，某些工件部分表面存在腐蚀或污染，导致激光反射率不均匀，造成光带图像离散性较大；或者工件表面的金属材料导致的反光严重，造成光带图像受环境影响大，质量低。针对上述应用背景，文中提出了一种结合极值法与Steger法的中心线提取算法，以消除或减弱复杂环境对算法提取中心线带来的影响。

1 基本原理

1.1 结构光光带特性

激光器产生激光的基本原理是大量粒子的受激辐射现象，光学共振腔中的粒子受到入射光子感应或激励，持续辐射出与入射光子特征完全相同的大量光子就是激光[9]。一般的线激光光源是由点激光光源穿过柱面镜和球面镜组合产生，其光束横截面上的光强能量呈高斯分布，因此调制到图像传感器上的光带截面灰度值可用近似高斯模型来描述：

(1)

现有结构光光带中心线提取算法主要分析光带的三个特性，即光带中心点位于光带横截面的灰度零阶极大值，一阶过零点，二阶极小值处(如图1所示)[10]。

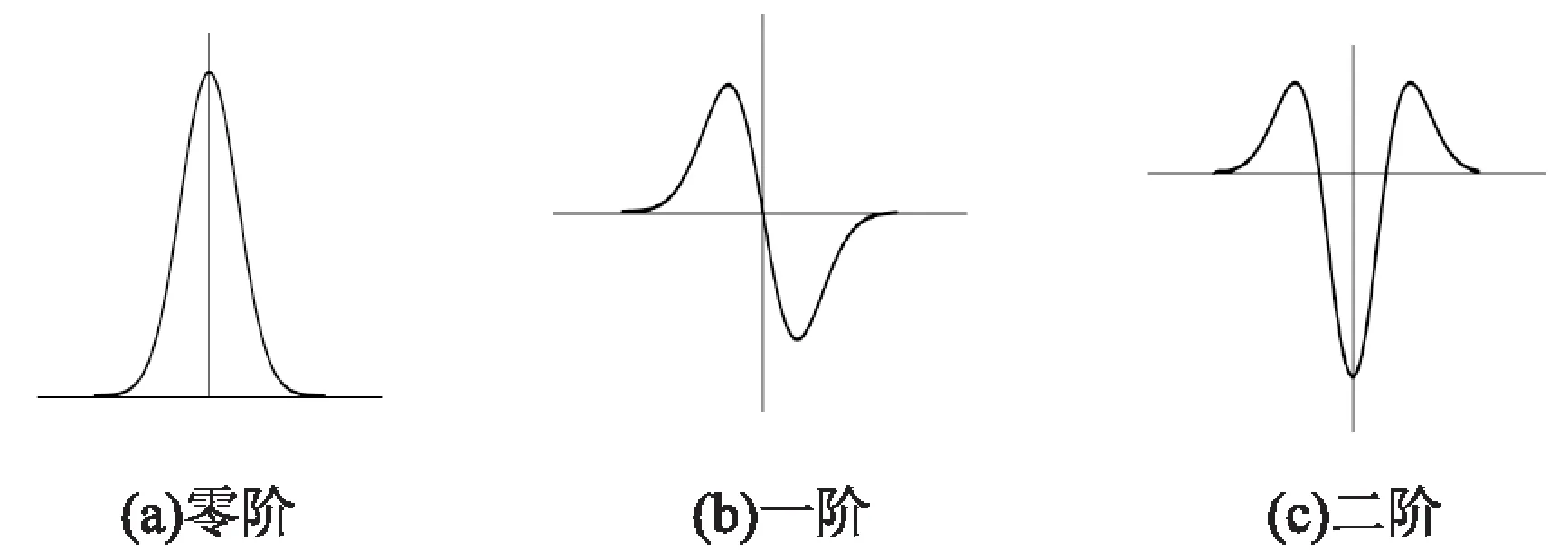
图1 结构光带截面灰度值的零阶、一阶、二阶特征

1.2 极值法

极值法是简单的光带中心线提取算法，利用光带中心点位于光带横截面灰度的极大值处这一特性，找到光带横截面极大值即可获得光带中心(见图2)。该算法快速简单，能达到像素级的精度。

1.3 基于Hessian矩阵的Steger算法

Steger算法将图像看成二维函数，在光带法线方向上将光带灰度分布按泰勒多项式展开，求取多项式的极大值所在位置，即为光带中心。为了得到图像的泰勒多项式，需要获得图像的偏导数，图像的偏导数rx,ry,rxy,rxx,ryy通过图像分别与下面式子中的高斯核进行卷积获得[11]。

图2 极值法受噪声的影响

(2)

(3)

(4)

(5)

(6)

则对于某一像素(x0,y0)，图像二阶泰勒展开有：

r(x,y)=r(x0,y0)+[(x-x0)(y-

(7)

该点的Hessian矩阵为：

(8)

该点法线方向(nx,ny)及该方向的二阶导数，分别为该点Hessian矩阵的最大绝对特征值和相应的特征向量。

光带图像r(x,y)中，在光带方向上的一阶方向导数为0，且二阶方向导数取负的极小值点，位于光带中心上。设光带方向n(x,y)用单位向量(nx,ny)表示，则式7沿光带方向(nx,ny)可以表示为：

r(x0+tnx,y0+tny)=r(x0,y0)+tnxrx(x0,y0)+

(9)

因光带方向上的一阶导数为零，则有：

(10)

由式9和式10可得：

(11)

则图像灰度的极值点为(px,py)=(x0+tnx,y0+tny)，即光带中心的一阶导数过零点，且(nx,ny)方向上的二阶方向导数小于指定阈值，则点(px,py)为光带的中心点[12-13]。

2 改进的极值法与自适应线宽Steger法中心线提取

为了处理光带离散性差、线宽不均匀、高反光的激光图像，算法运用运算量少的极值法确定出光带每一行截面宽度，得到粗略的光带区域；然后再结合自适应线宽Steger法计算出光带中心的亚像素位置。

2.1 光带图像预处理及ROI提取

线结构光投射器将激光投射到被测物体表面，利用CCD相机采集图像。通常情况下，因为环境的复杂性，往往会给提取激光光带带来一定的干扰。为了防止这些环境所带来的干扰，往往用CCD相机连续采集多张测量图像，通过图像序列做差获得只有激光光带的测量图像，避开了环境复杂性的干扰。

这时得到的激光光带的图像通常具有较高的对比度，因此采用基于大津法(Otsu算法)[14]选择适应的阈值，然后用这个阈值对图像进行二值化处理，并且再进行一系列的腐蚀和膨胀操作，把感兴趣区域(ROI)从背景中提取出来。不仅能有效减少环境噪声对后续光带中心提取的影响，而且能明显提高光带提取速度，满足测量系统对实时性的要求。

2.2 粗略光带区域提取

在现实环境下，被测物体表面往往有缺陷、环境反光等干扰因素，得到的激光光带图像的光带宽度很有可能不一致，所以直接进行光带中心线提取达不到精度要求。为了解决这个问题，首先运用改进的极值法粗略提取光带区域，然后再精确提取光带中心。文中算法首先通过寻找每一行最大像素值和最大像素值0.9倍所在的坐标，通过这两个坐标计算出光带粗略中心；然后算法设定最大光带宽度阈值为40个像素值，排除反光现象造成的错误光带，具体方法是光带宽度大于40的部分进行截断，其他正常光带部分寻找到最低光带边缘后左右再增加5个像素点的值，以保证光带包含全部光带区域。

再采用参数为5个像素的中值滤波(median filtering)对粗略光带区域进行处理，以解决由于光带离散性差和反光带来的光带宽度差异太大的问题；最后对光带区域每行用参数σ=0.5，窗口宽度为3的高斯核进行高斯滤波，去除光带中的杂点和高频噪声。经过上述一系列图像处理，得到了最佳的光带区域。

2.3 光带中心亚像素提取

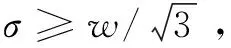
w(i)=

(12)

其中，M,N为光带行号。

观察Steger推导公式不难发现，每个点都要进行5次(rx,ry,rxy,rxx,ryy)二维高斯卷积，会导致算法运算量很大。从式2～6可以看出，二维高斯核可以等效分解为一次高斯行卷积和一次高斯列卷积，这样对于大模板的卷积计算将会从根本上减小计算量。

3 实验分析

为了验证算法的有效性和准确性，实验利用基于三角测量法的线结构光测量系统，选取两种表面平整的平面物体作为测量对象，分别对其表面进行光带中心线提取。实验拍摄到的光带图像如图3所示。图(a)表示测量物体表面光滑、反射率均匀，无反光现象，可以看到激光图像质量较好；图(b)表示测量物体表面反射率不均匀、存在较严重的反光现象，可以看到激光光带图像比较离散，反光较为严重，质量不高。

图3 平面物体实验图像

采用相同线宽和其他滤波参数对两幅光带图像进行预处理，然后分别用灰度重心法、基于Hessian矩阵的Steger方法和文中算法对图3所示图像提取光带中心。由于实验采用的测量对象是物体平面，因此分别对结果直线拟合，计算所有数据点到拟合直线的均方差。在同样测量条件下，若各数据点到拟合直线距离的均方差较大，则表明测量精度较低，说明算法提取光带中心相对不准确；反之，如果数据点到拟合直线距离的均方差较小，则说明算法提取光带中心相对准确[15]。表1为运用三种算法对两种实验光带图像进行多次中心线提取，计算得到的数据点到拟合直线均方差的平均值。

表1 三种算法均方差对比

从表1可以看出，对于亮度均匀、质量较好的光带，三种算法求出的数据点到拟合直线距离的均方差较小且差别不大，提取到的光带中心线较准确；而对于光带较离散、质量较差的情况，灰度重心法的均方差已偏离很大，而文中算法的均方差优于其他两种方法，能比较精确地提取光带中心线。

为了进一步验证该算法对复杂环境的适应性，将其应用到存在高反光特性的金属测量工件。图4(a)为测量工件不同平面在CCD相机中调制得到的光带图像，离散性差，且表面存在的高反光特性导致光带截面不再呈高斯分布。图4(b)为算法第一步处理得到的光带二值化图像。图4(c)为算法得到的最佳光带区域图像。图4(d)为利用文中算法得到的结构光光带中心。

图4 实验结果图像

4 结束语

实际工程应用中，针对三维测量图像处理系统中结构光光源质量、物体表面反光，或摄像机采集图像质量等环境因素对结构光中心线提取的影响，提出了一种结合极值法与Steger法的中心线提取算法。该算法首先利用极值法初步确定光带区域，然后利用自适应线宽的Steger法计算出光带中心亚像素位置。实验结果表明，该算法能快速有效地提取光带中心，具有良好的测量精度和稳定性，在光带图像质量低、测量物体存在反光现象等复杂环境下仍能比较准确地提取光带中心位置。该算法为后续的各种图像测量系统提供了良好的精度保障，具有一定的实用价值。