基于谈判的物流企业运输协同

刘长贤，田厚平

（1.南京邮电大学 管理学院，江苏 南京 210003；2.南京理工大学 经济管理学院，江苏 南京 210094）

1 引言

近年来，随着经济快速发展和电子商务高速增长，物流行业运输量呈现快速增长趋势。以2017年为例，国家邮政局统计数据显示：该年度邮政行业业务收入6 622.6亿元，同比增长23.1%。其中邮政寄递服务业务收入累计完成353.5亿元，同比增长15.2%；快递业务收入完成4 957.1亿元，同比增长24.7%[1]。国内物流企业发展进入了快车道。

伴随物流发展的是对时间越来越敏感的消费者需求。以在线市场为例，越来越多的网络购物者希望实现当天送达或隔天送达等快捷物流服务。显然，该要求对物流企业提出了新的挑战：如何为顾客提供快速物流服务，并有效控制物流成本、提高企业利润？

越来越多的物流企业对此给予了高度重视，并试图通过“协同物流”加以应对。显然，随着运输量快速增长，企业的任务越来越多、车次越来越频繁。因而如何通过协同运输，实现1+1＞2的效果，是企业界和学术界不得不面临的重要问题。

针对以上问题，现有文献进行了部分探索：Krajewska等（2008）[2]较早研究了协同运输问题。考虑多个物流企业（每个企业均有自己的配送节点和配送时间要求），研究了这些企业如何进行合作以确定最优配送方案的问题。同时，还给出了基于Shapley值的合作利益分配方案。结果表明协同运输能够有效控制物流成本、实现企业双赢。李军和蔡小强（2007）[3]进一步研究了对时间敏感的易腐性产品运输问题。基于合作博弈理论建立了易腐品运输成本优化模型，分析了成本分配博弈的核仁并给出了运输费用分配方案。曹郅和窦志武（2018）[4]还研究了同城物流协同运输问题。考虑到两个同城物流企业，分析了协同运输所带来的利润和成本。结果表明与独立运输相比，协同运输能够带来更多利润、更低成本，同时供应链整体收益也比协同前有所提高。Hsu等（2017）[5]则从采购物流的角度进行了研究。基于Nash谈判理论，研究了两个零售商（一个强势而另一个相对弱势）向同一供应商采购的采购决策问题。结果表明与独立采购相比，强势零售商总是偏好于联合采购，而弱势零售商却不总是如此。

上述文献对协同物流的研究卓有成效。然而，这些研究常常是基于某一特定方案进行的，而现实中谈判双方对谈判方案的偏好常常出现不一致性。以协同运输为例，某企业可能选择对自己最有利的Shapley谈判模型，而另一方则可能选择对自己最有利的Nash谈判模型，从而出现谈判方案的不一致性。这促使人们进一步思考：如果谈判各方对谈判方案的偏好不同，那么谈判又该如何进行？最后的结果又会如何？

分析现有的谈判理论，可以看到除Shapley值、Nash谈判模型之外，还有MCRS、Raiffa裁决方案等不同的谈判方案。而每种谈判方案在现实中都可能会被采用。例如Krajewska等（2008）[2]、Shapley（1953）[6]认为如果每个合作者都对自己的贡献比较看重、并据此分配利益时，Shapley值是一个可行选择。而Nash（1950）[7]则从几个公理出发，认为在这几个公理满足条件下Nash谈判模型也是可行选择。其后，田厚平（2004）、Baron等（2016）还从可信威胁、谈判破裂点等角度进行了研究[8-9]。MCRS方法则对谈判问题进行简化，只考虑成员加入联盟时带来的贡献，并据此对合作收益按比例分配[10]。岳超源（2017）[10]、Raiffa（2007）[11]则指出，Raiffa裁决方案可以综合考虑成员加入联盟时带来的贡献以及不加入联盟对自己的不利影响。

综上，人们从不同角度出发对谈判问题进行了较为深入的探索。然而，一个重要的、亟待解决的问题是：由于不同谈判方案会得到不同的谈判结果，显然每个成员都愿意采取对自己最有利的谈判方案。那么，何种方案将会得到大家的认同并被最终采纳？目前在文献中鲜见有关谈判方案选择问题的研究。

本文就上述问题进行了针对性研究。探讨了Nash谈判方案、MCRS、Shapley值、Raiffa裁决方案等4种谈判方案，分析了每种方案的含义及特点。提出了谈判方案的选择方法—基于TOPSIS的多指标综合决策方法。在此基础上，以物流企业协同运输为例，给出了一个三方合作谈判算例。结果表明，在本谈判问题中最优谈判方案很可能是Raiffa裁决方案。

2 几种典型的谈判方案

合作利益分配中存在着较多的谈判方案。其中以Nash谈判方案、MCRS、Shapley值、Raiffa裁决方案等较为典型。以下给出每种方案的具体算法，并对其原理及含义做出分析。

2.1 Nash谈判方案

早在20世纪50年代，Nash进行了一系列谈判研究，并提出了Nash谈判方案。

对两个谈判者，记不合作收益为(v1,v2)，合作收益为v12，合作收益分配方案为(x1,x2)。基于五个公理（方案有效性、个体理性、对称性、线性效用变换不变性、无关选择独立性），给出了谈判方案[7]。它可通过如下模型得到：

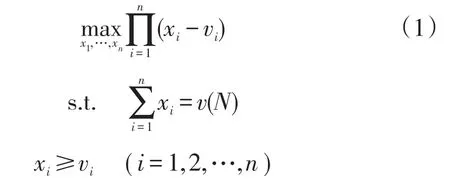
其中，v(N)为n人合作联盟的总收益。注意到Nash谈判解是基于上述公理得到。该解数学意义较强，但不够直观和容易理解。同时，对于“无关选择独立性”公理目前存在一些争议。部分学者认为谈判可行域反映了谈判者的实力，在谈判中没有“无关方案”。

2.2 MCRS

MCRS方法中联盟利益分配按比例进行。首先确定利益分配的上下界：

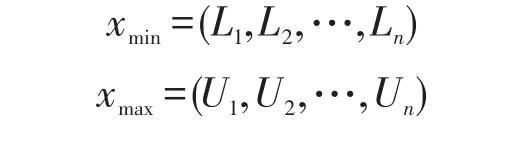
这里Ui=v(N)-v(N-i)。其中，v(N)表示所有局中人组成的联盟总收益，v(N-i)为除成员i之外的其他n-1个成员所组成的联盟，即Ui表示成员i加入联盟N-i时给联盟所带来的贡献；Li为成员i单独行动时的收益。

记成员i的利益分配值为xi，则该值应满足xi∈[Li,Ui]。根据每个成员收益成比例原则，有如下方程组：

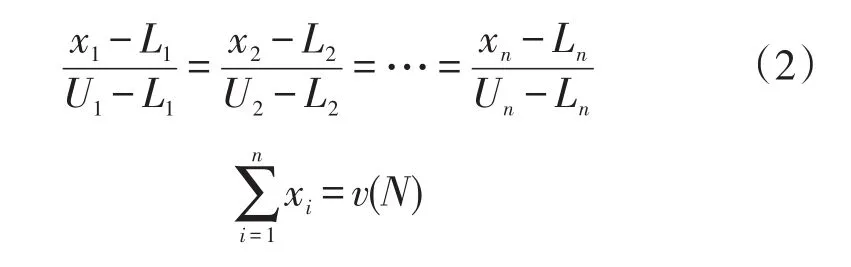
求解该方程组，即可得到每个成员的利益分配值x=(x1,x2,…,xn)。

该方案计算量较少。但它没有考虑成员i加入每个可能的联盟为联盟所带来的收益问题。

2.3 Shapley值

对于合作利益分配问题，1953年Shapley给出了一种利益分配方案。该方案考虑到成员i加入每个可能的联盟为联盟所带来的收益问题。认为合作利益的分配是合作者参与所有合作贡献的加权平均值。利益分配值由式（3）给出：

式中s表示联盟S的局中人个数，N表示所有局中人组成的集合，n为所有局中人个数。v(S)表示联盟S的合作利益，v(S-i)表示集合S中除成员i之外剩余人员组成的联盟。xi为局中人i在合作中所得到的收益。

Shapley值具有如下概率意义：考虑成员i参与所有可能联盟为联盟创造的价值，Shapley值就是局中人i参与合作的期望收益。

该方法计算量较多，遵循“论功行赏”原则，但没有考虑不加入联盟时联盟对自己的威胁。

2.4 Raiffa谈判方案

该方法综合考虑到加入联盟给联盟带来的贡献以及不加入联盟时联盟对自己的威胁。依结盟的先后顺序对联盟合作利益进行分配（具体算法见表2）。该方法与Shapley值有类似之处，他们都遵循“论功行赏”的原则，不过Raiffa谈判方案还考虑到不加入联盟时联盟对自己的威胁，其缺点是计算量较多。

3 谈判方案选择标准

同一个谈判问题存在较多的谈判方案，而不同方案将得到不同的谈判结果。那么面对一个具体谈判问题时，何种谈判方案使全体成员都能够接受并较为满意，就是一个具有重要理论和实际意义的问题。

在谈判方案选择上，本文认为可以借助多指标综合决策的思路来进行。首先在评价谈判方案的有效性前，将多个谈判方案的计算结果进行平均，得到这些方案的平均值，称其为平均方案。

对谈判方案选择，本文认为可以结合以下两个标准进行：

（1）选择的谈判方案，应使群体满意度要高；

（2）在标准（1）基础上，进一步地如果其中某些方案的群体满意度都较高且差异较小，则从中选出与平均方案差异最小的方案作为最终方案，该方案更有可能接近实际谈判结果。

4 谈判方案选择方法

记某谈判有n个不同利益谈判者，通过m个谈判方案得到m个谈判结果。该结果如下所示：

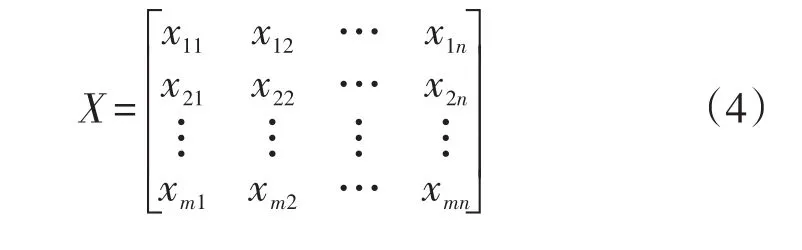
其中，xij表示使用谈判方案i时成员j所获联盟利益分配值。将n个谈判者分别记为指标(x1,x2,…,xn)，m个谈判方案分别记为（O1,O2,…,Om）。这里，每个指标都为极大型（越大越好）。则每种谈判方案都是联盟利益在这些指标上的分配。

这样，谈判方案选择可转化为多指标综合决策来解决。而多指标决策领域有较多的综合评价方法。为客观评价各个谈判方案的优劣，本着方法科学、原理简明、计算量小的原则，采用客观综合评价方法—TOPSIS（逼近理想解的排序方法）。该方法步骤如下：

（1）确定正负理想点

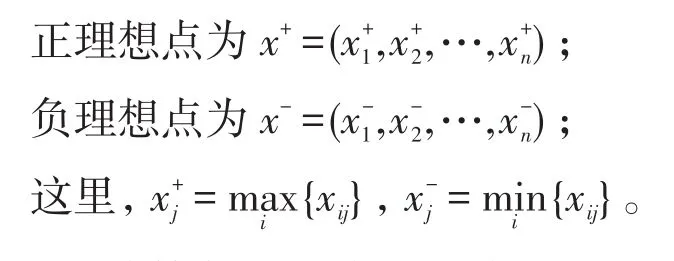
（2）计算每个方案与正负理想点之间的距离。记各个方案与正理想点之间的距离为与负理想点的距离为则为谈判方案i与正理想点x+（负理想点x-）的距离。

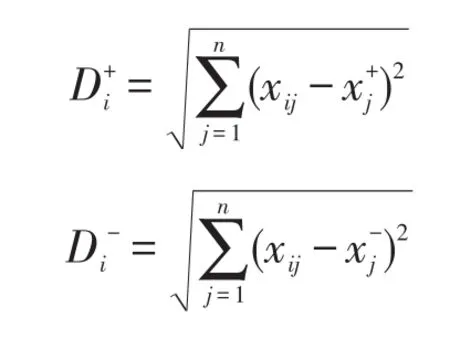
（3）根据相对接近度对方案排序。记每个方案与理想点的相对接近度为Z=(z1,z2,…,zm)。这里该值表示谈判方案i与理想点之间的接近程度。zi越大，谈判方案i与负理想点距离越大，而与正理想点的距离越小。根据相对接近度Z，可将各个谈判方案从大到小排序。

本方法根据每个方案与正负理想点的距离进行排序，既靠近正理想点又远离负理想点的方案就是方案集中的最优方案。通过TOPSIS方法将各个谈判方案排序后，最终谈判方案的选择可以根据上文“谈判方案的选择标准”来确定。

5 协同运输谈判算例

在某一地区具有甲乙丙3家物流公司，他们面临单独运营还是协同运输问题。合作与单独营运的收入情况见表1。

表1 合作与独立运营收入（单位：拾万元）

三家公司能否合作取决于合作利益分配是否公平合理，且每个企业合作时的收入应高于不合作情形。否则合作将会失效。

针对上述问题，分别采用Nash谈判方案、MCRS、Shapley值以及Raiffa谈判方案等4种方案进行合作利益分配（数据精确到小数点后两位），通过这些方案的比较，给出最优方案。

5.1 Nash谈判方案计算结果

根据Nash谈判方案，有以下利益分配模型：

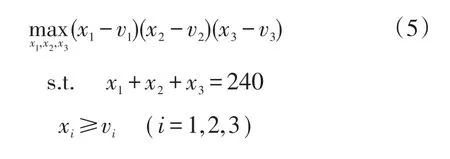
这里，谈判冲突点为v=(54,50,45)，即最坏情况下每个企业的收入。求解该模型，得到Nash谈判下的利益分配方案：

5.2 MCRS计算结果

三个企业的最大可能收入xmax=(U1,U2,U3)=(240-120,240-160,240-140)=(120,80,100)。其中，U1=240-120表示企业甲的最大可能收入为三家企业合作总收入与乙丙两家企业合作收入之差，其余类推。三个企业的最低可能收入为xmin=(54,50,45)。根据MCRS谈判方案，有：

5.3 Shapley值计算结果

根据Shapley值计算式，有：

则有利益分配方案：

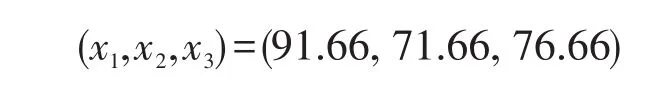
5.4 Raiffa谈判方案计算结果

对于Raiffa谈判方案，结果见表2。

6 谈判方案的选择

综合上述结果，得到不同谈判方案下联盟利益分配情况，见表3。

根据上文“谈判方案选择方法”，将每个成员视为某种谈判方案下的指标，则联盟利益谈判实际上就是合作收益在这些指标上的分配。这样，谈判方案选择可转化为一个具有4个被评价方案、3个被评价指标的综合评价问题。

6.1 谈判方案初步比较

表2 基于Raiffa方案的利益分配

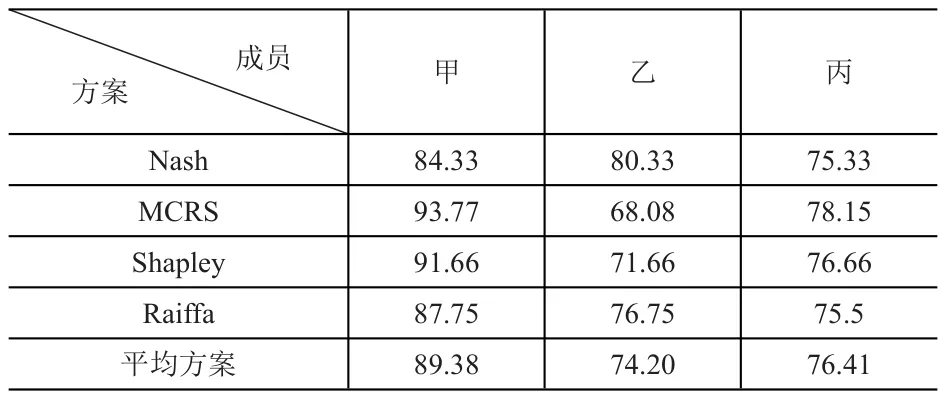
表3 不同谈判方案的联盟利益分配表

为客观评价各个方案优劣，采用客观综合评价方法—TOPSIS进行方案初步比较。

记表3所述数据为矩阵X，则xij表示在使用谈判方案i时企业j所获利益分配值。这里每个指标均为极大型。由于三家企业谈判地位相同，没有隶属关系，因而每个企业的重要性权重都为1/3。将表3数据进行加权计算，则有：

对矩阵X，按以下步骤进行方案评价：

（1）确定正负理想点。正理想点为x+=（31.26,26.78,26.05）；负理想点为x-=（28.11,22.70,25.11）。

（2）计算每个方案与正负理想点的距离。这五个方案与正理想点之间的距离为D+=（3.28,4.08,3.02,2.50,2.58）；与负理想点之间的距离为D-=（4.08,3.29,2.75,3.11,2.67）。

（3）根据相对接近度对方案排序。各个方案与理想点之间的相对接近度为Z=（0.55,0.45,0.48,0.55,0.51）。zi越大，表明谈判方案i与正理想点越近。故有谈判方案排序见表4。

表4 谈判方案排序

表4显示Nash谈判方案与Raiffa方案排序相同，都处于第1位。以下做进一步比较。

6.2 谈判方案进一步比较

根据文中“谈判方案的选择标准”，采用表3数据（也可采用矩阵（7）所示数据），将各个方案与平均方案进行比较，得到各方案与平均方案的距离，见表5。

表5 各个谈判方案与平均方案的距离

可以看到，表4显示Raiffa方案与Nash谈判方案不分高下；进一步考虑到表5，则Raiffa方案对本谈判问题的解决可能会更好。

综上，本协同运输谈判中最优分配方案很可能是Raiffa裁决方案。

7 结束语

针对协同运输利益分配问题，本文研究了四种典型的利益分配方案—Nash谈判方案、MCRS、Shapley值以及Raiffa裁决方案，分析了每种方案的含义及特点。由于不同方案会得到不同的利益分配结果，而每个成员都愿意采取对自己最有利的利益分配方案。因而还给出了基于TOPSIS的方案选择标准。结果显示本文提出的利益分配方案能够取得较好的协调效果。

进一步研究可以考虑协同运输谈判实验，并与实际谈判进行对比研究，以更清晰地刻画协同运输利益分配方案的有效性。