基于SACS的海上风电机组支撑结构管节点疲劳分析和优化

2018-09-20蒲春旭

风能 2018年6期

文 | 蒲春旭

海上风电机组长年要承受风浪等恶劣环境载荷的作用，再加上海水腐蚀，支撑结构管节点很容易产生疲劳，通常只要少数节点发生疲劳破坏，就有可能造成整个工程结构事故。因此，当支撑结构设计完成后，需要对危险部位的管节点进行疲劳分析和优化。

目前波浪载荷作用下的焊接管节点的疲劳评估主要采用谱疲劳分析方法，由于该方法快速有效而且较为精确，因此被广泛应用于单桩和三桩海上风电机组支撑结构的疲劳分析中。在完成海上风电机组支撑结构的疲劳校核之后，如果发现有不满足疲劳设计要求节点，则需要对该节点进行局部的加强和优化。针对管节点的加强优化等问题，世界各国的研究者都做了许多的研究，主要针对典型T型管节点加固与不加固的承载力和疲劳强度问题，研究结果表明采用管节点加强能大大降低热点应力，提高疲劳寿命。

本文介绍了波浪谱疲劳分析的基本原理和流程，然后以导管架式海上风电机组支撑结构为例，采用SACS软件对其进行了波浪载荷作用下的疲劳分析，最后针对不满足疲劳要求的管节点进行了加强优化研究，并对加强后的管节点重新进行了疲劳分析。SACS软件能够实现海上风电机组支撑结构的谱疲劳分析和管节点的优化设计，这为海上风电机组支撑结构的设计提供了一条高效的途径，对保证支撑结构在设计寿命期内的安全运行具有重要意义。

波浪载荷作用下谱疲劳分析基本原理

在波浪载荷作用下，管节点的详细疲劳分析可分为时域疲劳分析和频域疲劳分析（又称谱疲劳分析），其中时域疲劳分析比较精确，但是将耗费大量的时间和成本；频域谱疲劳分析方法也是目前公认的较为精确的疲劳评估方法，相比时域疲劳分析，它将会节省大量的计算成本。因此，本文采用谱疲劳分析方法来计算波浪载荷作用下海上风电机组支撑结构管节点的疲劳损伤。

谱疲劳分析法是船舶与海洋工程中一种常用的研究载荷和结构响应的方法，它的理论基础是随机过程理论中的线性系统变换，作用在结构上的波浪过程是系统的输入，结构内由于波浪作用引起的交变应力则是系统的输出响应（图1）。

谱疲劳分析的基本流程见图2。

图1 线性动力系统

图2 谱疲劳分析的基本流程

一、绘制波浪散布图

依据有效波高和周期把波浪环境分为几种海况，通常取8种海况，并统计每种海况出现的概率。

二、选取海浪谱

波浪谱选择Pierson-Moscowitz谱，简称P-M谱。此谱属于经验谱，是根据北大西洋的实测资料经过筛选得到，所依据的资料比较充分，分析比较合理，使用比较方便而且可以直接积分，在船舶与海洋工程中得到广泛应用。

三、波浪载荷计算

作用于导管架的载荷是依据随机理论对莫里森方程进行傅里叶变换得到。由于谱疲劳分析方法是基于线性叠加原理，因此，方程中水质点速度和加速度按线性波理论计算，阻力项要进行线性化。

四、应力的传递函数

传递函数是表征结构某处在某一波浪频率下和单位波高产生的应力范围。在谱疲劳分析方法中，传递函数是最关键的参数，一般可通过软件计算得到。

式中，H（ω）为结构应力的传递函数，Sσ（ω）为结构应力响应谱，Sη（ω）为选取的波浪谱，ω为波浪频率。

传递函数的计算方法：在一系列频率值ω1，ω2，，ωn中对于每一频率ωi的规则波进行结构动力学分析，然后提取疲劳校核点的应力幅值。

五、热点应力的计算

根据规范，需要使用校核部位的热点应力进行疲劳计算。热点应力可根据名义应力乘以应力集中系数得到，即：

式中，σhot-spot是热点应力，σno min al是名义应力，SCF是应力集中系数，具体的计算方法将在下文介绍。

（一）名义应力

名义应力大小等于原始载荷除以原始的截面积。名义应力不考虑焊缝的几何不连续以及焊缝缺陷导致的应力集中，只与施加的外部载荷、管的截面积等参数有关。一般来讲，管节点承受的载荷分为轴向载荷（Axial Load，如图3a）、面内弯曲载荷（In-plane Load，如图3b）、面外弯曲载荷（Out-plane Load，如图3c）以及这3种载荷之间的组合。对于管节点来说，三种简单载荷作用下的名义应力见式（3）—（5）。

1. 轴向载荷作用下：

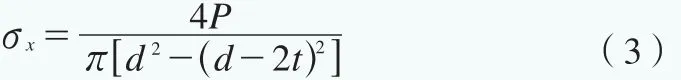
2. 面内弯曲载荷作用下：

3.面外弯曲载荷作用下：

式中，P为施加在撑管上的轴向力，M为施加在撑管上的面内弯矩和面外弯矩（见图3），d为撑管的直径，t为撑管的厚度。

（二）热点应力

在波浪载荷作用下，容易产生疲劳的热点部位一般为管节点弦管与撑管焊接的交贯处，如图4所示。在相贯线处，每隔45一个热点，分别为T、TR、R、BR、B、BL、L、TL，弦管和撑管各8个部位，T代表top，B代表bottom，L代表left，R代表right。对于采用shell单元建模的管节点，热点应力可以通过第一主应力的线性外推得到。而对于采用杆梁单元模拟的管节点，热点应力可以通过轴向应力，面内弯曲应力和面外弯曲应力的加权叠加得到，见式（6）—（13）。

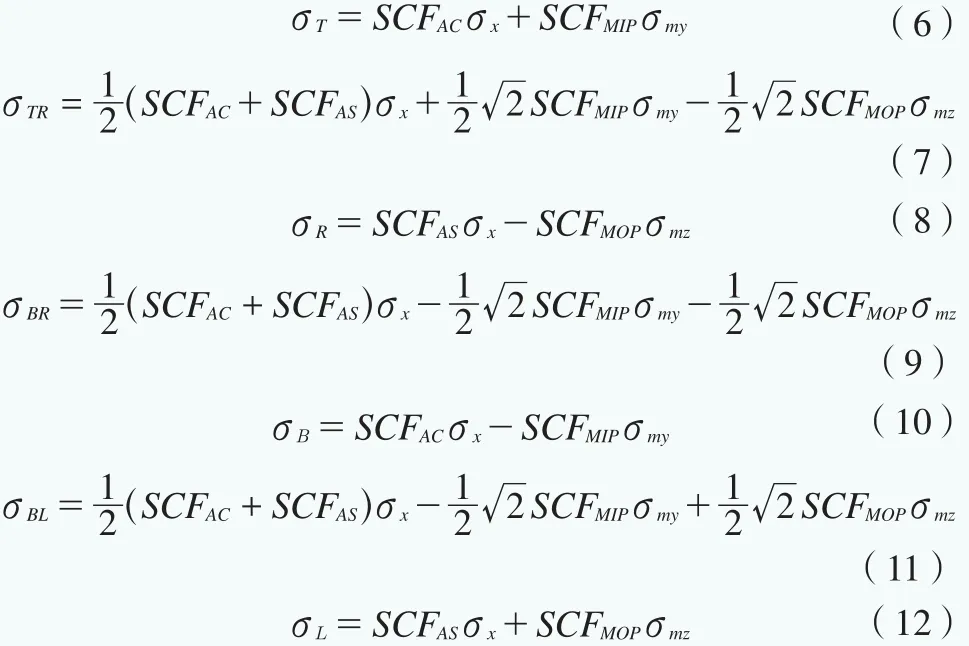
图3 管节点承受的轴向载荷，面内弯曲载荷和面外弯曲载荷

图4 热点应力位置分布

式中，σx、σmy和σmz是在轴向载荷、面内弯曲载荷和面外弯曲载荷作用下的最大名义应力，SCFAS和SCFAC是在轴向载荷作用下鞍点和冠点处的应力集中系数，SCFMIP和SCFMOP分别是面内和面外弯曲载荷作用下的应力集中系数。

六、 S-N曲线

疲劳的设计是基于S-N曲线的，S-N曲线数据一般是通过试验测定并将数据拟合而得到的。S-N曲线具有97.7%的生存概率。

不同的焊接形式，对疲劳所产生的影响也不同。所以，在实际的疲劳设计中，通常将焊接节点分成几种不同的类别，每一种焊接节点都有与其相应的曲线。对于海洋工程中的钢质焊接管节点，本文采用的S-N基本方程式如式（14）所示。

式中， m为S-N曲线的斜率；loga-为S-N曲线与坐标轴的交点；tref为参考厚度（对于非管节点焊接连接结构，取25mm，当厚度小于参考厚度tref时，t取值为tref，当厚度大于参考厚度tref时，取实际厚度。对管状节点，参考厚度取值为32mm）；t为疲劳校核部位的厚度；k为疲劳强度厚度指数。

本校核选取S-N曲线为D曲线，具体参数如表1所示，参考厚度取值为32mm。

七、应力范围短期分布和波浪载荷致疲劳损伤计算

确定应力功率谱密度后，根据随机振动理论，假设每个海况的应力范围都服从瑞利分布，则有：

f（S）是一个瑞利分布函数，σ0是应力过程的标准差，可以通过应力功率谱密度积分计算得到。

根据Miner准则，疲劳损伤可根据下式进行计算：

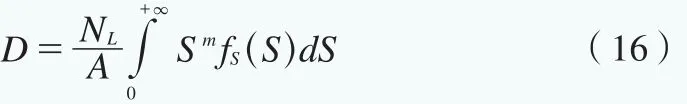
Sm的期望为：

所以损伤的解析解计算公式为：

式中，m是S-N参数。当m＝3时，A＝1012.164；当m＝5时，A＝1015.606。

应力响应的功率谱函数的n次矩：

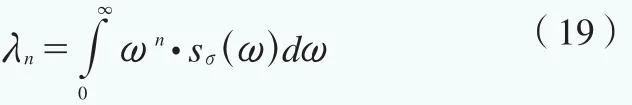
计算平均跨零率：

式中，λ0、λ2分别表示应力谱函数的零次矩和二次矩，sσ（ω）为应力响应的功率谱密度。

设计寿命期内的循环次数可通过下式计算得到：

式中，T为海上风电机组的设计寿命，一般为25年。

当求出热点应力的功率谱密度函数之后，便可根据公式（18）计算其引起的疲劳损伤。

基于SACS海上风电机组支撑结构管节点疲劳分析

本节以某海上风电场6MW海上风电机组支撑结构为研究对象，该结构为四桩导管架式结构，工作水深为8～15m，桩基贯入深度为50m，桩基直径为2m。

疲劳分析过程采用SACS软件——专门用于海洋平台设计的有限元分析软件。它可以实现典型的固定式海洋平台、码头、承台以及浮式系统上部结构的静力分析要求和疲劳分析要求。

使用SACS软件对海上风电机组支撑结构进行了桩基线性化、模态分析和波浪动力分析，然后对支撑结构在波浪载荷作用下进行了疲劳分析，最后对易发生疲劳破坏的不同类型管节点进行了疲劳损伤计算。

一、SACS模型示意图

SACS模型中全部节点都视为刚性节点，同时每个构件的两端连接都视为刚性连接。导管被视为只承受导管架和下底板的水平力，不承受竖向受力的结构构件。

二、波浪环境

本阶段按照一年一遇各水位下的Hs（取H13%），保守考虑方向取为0°。波浪理论采用Airy线性波理论。P-M谱如图6所示。

表1 D曲线的参数

图5 SACS海上风电机组支撑结构模型

选取具有代表性一年波浪资料，建立表2所示的波浪散布图用于疲劳损伤计算。

图6 P-M谱

表2 波浪散布图

三、模态分析

采用SACS软件的DYMOD模块进行风电机组整机模态分析，整机基础和塔筒根据图纸模拟实际重量，叶片、机舱和轮毂的质量为1633kN，由质量点加在相应的质心，土壤由SACS软件的SUPER ELEMENT模块等效模拟成土弹簧作为模型的边界条件，计算了前10阶模态，对应的频率如表3。

由表可以看出，第一阶频率为0.329877，第二阶频率为0.326433，整机的允许频率范围为0.299～0.358，包含 5%的安全系数，因此，不会与整机发生共振。

表3 导管架模型前10阶模态的频率

四、波浪响应谱分析

为了使结构的自振周期附近出现明显的峰值，保证疲劳计算的准确性，SACS模型文件中的波浪周期的选择在接近平台一阶周期的区域中取的波浪要相对多些，这样才能保证波浪在结构的一阶自振周期附近响应最大。选取了25个波浪用来产生传递函数，波陡设置为0.05，前6个波的周期为 10s、9s、8s、7s、6s、5s，间隔 1s，其后 6个波的周期分别为 4.75s、4.5s、4.25s、4s、3.75s、3.5s，间隔 0.25s，再接下来的11个波周期为3.4～2.4s，间隔为0.1s，最后两个波周期为2.25s、2s。采用Airy波理论，每个波又分为18个子工况，总共25个波（450个载荷工况）来产生传递函数，SACS计算得到的传递函数如图7所示。

五、疲劳损伤计算

疲劳校核节点为：301L、303L、305L、307L、401L、403L、405L、407L、X34A、X34B、X34C、X34D、X45A、X45B、X45C、X45D，如图8所示（仅列举了部分管节点）。301L、303L、305L、307L四个管节点的分布按逆时针分布。

图7 热点应力传递函数

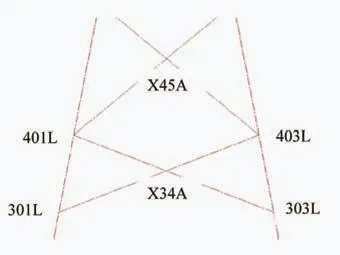
图8 疲劳校核管节点

在波浪载荷作用下，导管架支撑结构疲劳校核的结果见表4。从中可以看出，301L、303L、305L、307L、X34A、X34B、X34C、X34D、X45A、X45B、X45C、X45D等管节点的疲劳损伤都远小于1，满足疲劳强度的要求；而管节点401L和403L的损伤大于1，未能满足要求；405L和407L两个节点的损伤值接近于1。从安全保守的角度来说，需要对401L、403L、405L和407L这四个管节点进行优化，使其满足疲劳强度的要求。

管节点加强优化

一、管节点加强方式

改善管节点疲劳性能的方法有很多，如局部加厚法、内部增加加强环法。由已知的S-N曲线方程可知，增加厚度会降低管节点的局部热点应力，但是考虑到参考厚度的影响，增加厚度可能会增加管节点的局部有效热点应力。因此，本文考虑使用内部增加加强环的方法，一个典型的加强环形式如图9所示。

图9 管节点加强型式

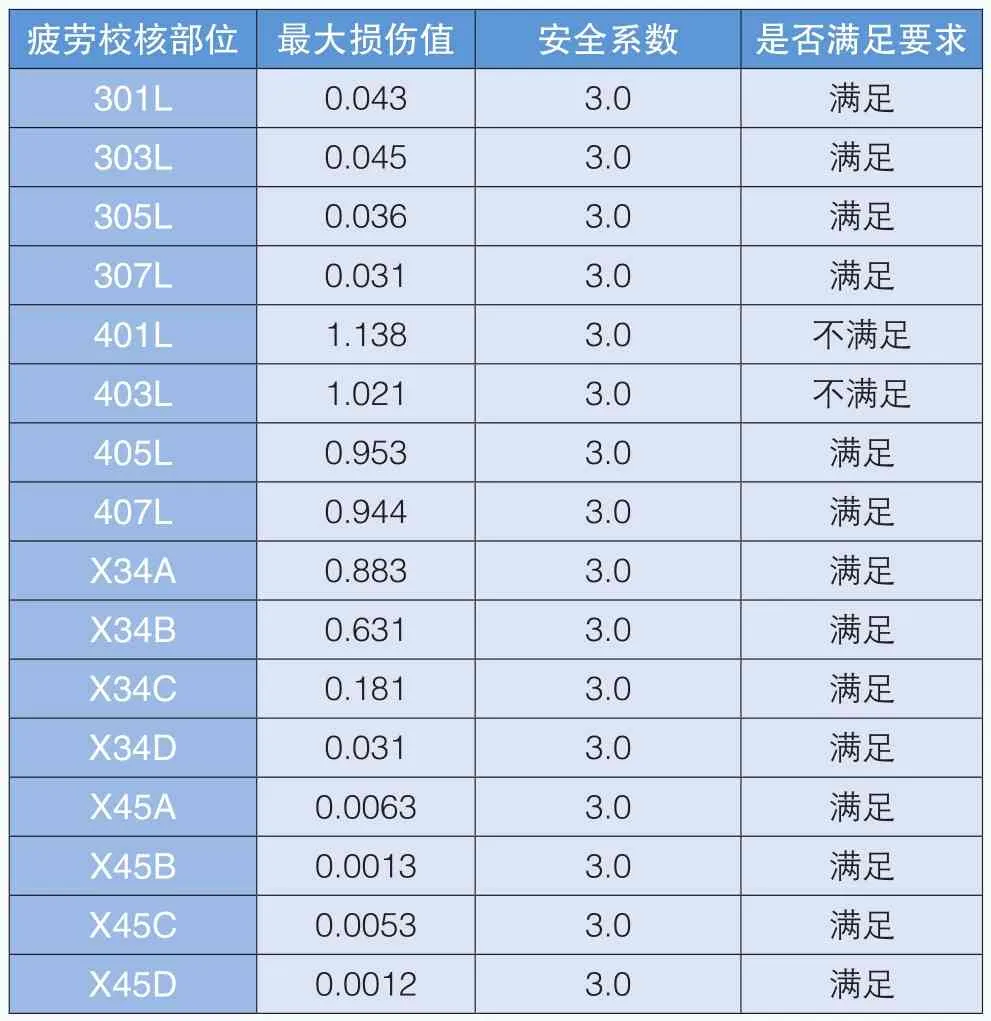
表4 管节点疲劳校核结果

研究表明，内部加强环在减小应力集中系数、改善疲劳寿命、提高极限强度等方面是非常有效的，并且内部加强环不会受到波浪的冲击、不易产生腐蚀疲劳，所以，可以在管节点内部采用加强环的形式。在北海区域的海洋工程结构中，至少存在2000多个采用内部加强环的关节点。

如果用有限元建模分析计算每个模型的应力集中系数，将会非常困难，并且耗费大量时间。因此，我们采用Murthy等人给出的参数公式计算加强管节点的应力集中系数，这组公式是采用130个模型通过有限元分析验证过的，因此，具有一定的可靠性。采用DNV规范中的参数公式计算未加强管节点的应力集中系数，为了方便研究，我们只计算了最大的应力集中系数，位置为弦管的鞍点处。具体加强环的应力集中系数见式（21）—（23）。

（1）轴向载荷作用下具有加强环的应力集中系数计算：