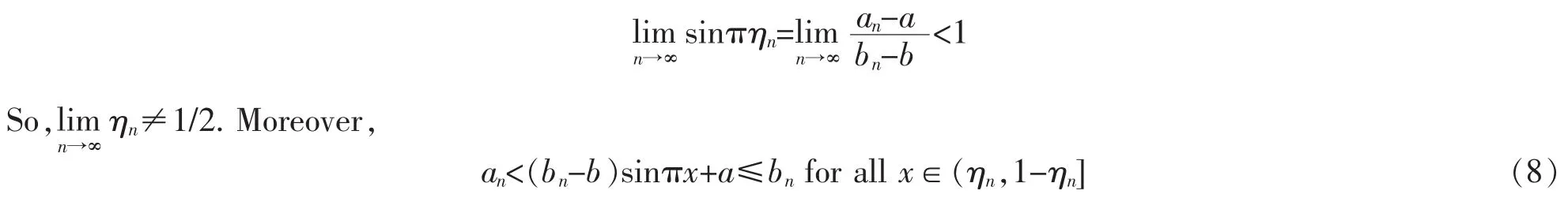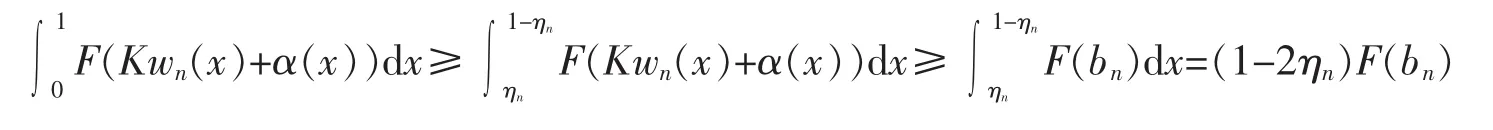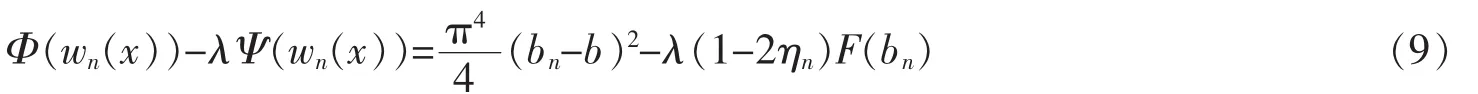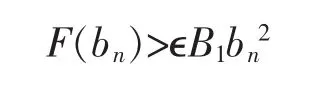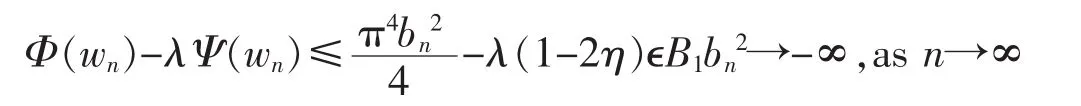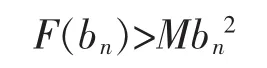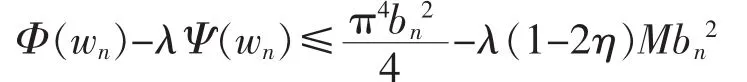Infinitely many solutions for a class of fourth-order equation with nonlinear boundary conditions

XI Lijing

（School of Mathematics and Physics，SUST，Suzhou 215009，China）

Abstract：This paper studies the existence of infinitely many solutions of the following fourth-order two-point boundary value problemswhere λ>0 is a parameter，f：R→Ris a continuous function，and a，c≥0，b≥a，d≥c，b－a≥c/3+d/6.By means of variational approaches，the existence of the infinitely many solutions is proved.

Key words： four-order boundary value problems；infinitely many solutions；critical points

1 Introduction and main results

Owing to the importance of higher order differential equations in Physics，existence and multiplicity of solutions such problems have been extensively studied，see for examples[1-10]and the references therein.In literature，various papers concern the following fourth-order boundary value problem

In particular，in[4]and[6]，the authors obtained the existence of infinitely many solutions for Problem（1）with λ=1 if f is an odd function.And in[1]，by employing the cone expansion or compression fixed point theorem，authors also got results on existence of infinitely many solutions for the problem（1）if f is monotone increasing.

In the present paper，motivated by [6，11-12]，we consider the problem which has perturbed boundary conditions

where λ>0 is a parameter，f：R→Ris a continuous function，and a，c≥0，b≥a，d≥c，b－a≥c/3+d/6.We establish a result on the existence of infinitely many solutions for Problem （2）by using the Riccer general variational principle（see[13]）.Here we introduce more general boundary conditions which are different from the above aforementioned works.Moreover，unlike in[1]，[4]and[6]，to obtain the existence of infinitely many solutions for Problem（2），we assume that f is neither odd nor monotone（see the following Theorems 1 for more details）.

Theorem 1Assume that the following conditions hold：

（F1）F（s）≥0 for all s>0，and

（F2）there exist sequences{an}and{bn}in（0，∞）withand bn→∞ such that f（s）≤0 for all s∈（an，bn），and

Then

（i）if B1<+∞，there exists λ*>0 such that，for every λ >λ*，Problem（2）has infinitely many solutions in C4[0，1]；

（ii）if B1=+∞，for every λ>0，Problem（2）has infinitely many solutions in C4[0，1].

2 Variational setting

In this section，we will see that Problem（2）has a variational structure.Let C[0，1]denote the usual real Banach space with the norm||u||C=maxx∈[0，1]|u（x）|.By L2[0，1]we denote the real Hilbert space with the inner productand the induced norm

It is well known that to find solutions of Problem（2）in C4[0，1]is equivalent to find solutions of the following integral equation in C[0，1]

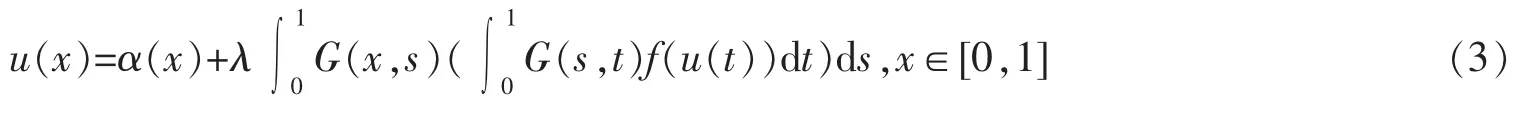
where α（x）=a+（b-a-c/3-d/6）x+（c/2）x2+[（d-c）/6]x3，and

It is easy to see that αmin=a，αmax=b and G is nonnegative，continuous and max（x，s）∈[0，1]×[0，1]G（x，s）=1/4.

Let w（x）=u（x）-α（x），then

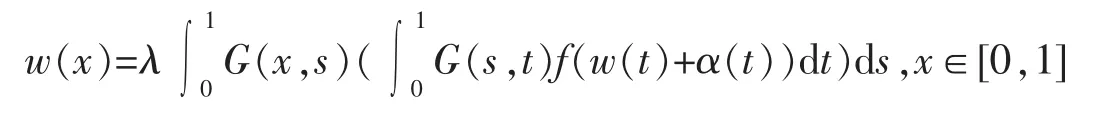
We respectively define operators K：L2[0，1]→C[0，1]and T：C[0，1]→C[0，1]as

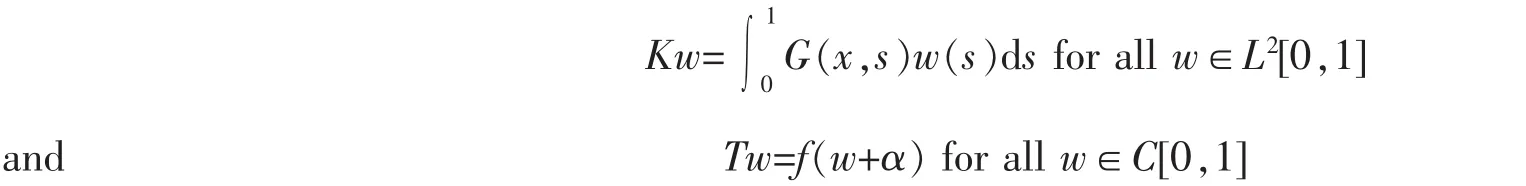
Then to find solutions of integral equation（3）in C[0，1]is equivalent to find solutions of operator equation

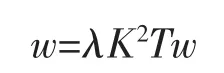
in C[0，1].For the linear operator K，we have the following properties.

Lemma 1[6]

（i）K：L2[0，1]→C[0，1]is a linear completely continuous operator，and K：L2[0，1]→L2[0，1]is also a linear completely continuous operator；

（ii）（Ku，v）=（u，Kv）for all u and v in L2[0，1]；

（iii）the operator equation w=λK2Tw has a solution in C[0，1]if and only if the operator equation v=λKTKv has a solution in L2[0，1].Moreover，w=kv and v=KTw.

Remark 1

（a）By the definition of K，we can obtain that Ku≠0 for all u∈L2[0，1]with u≠0.Therefore，Ku1≠Ku2for all u1，u2∈L2[0，1]if u1≠u2.

（b）It is easy to see that the eigenvalues of K are 1/n2π2and the corresponding eigenvectors are sinnπx，n=1，2，…

（c）For any u∈L2[0，1]，it follows from the definition K that

Lemma 2LetThen

（i）I is Fréchet differentiable on C[0，1]and I′（w）u=（Tw，u）for all u，w∈C[0，1]；

（ii）I◦K is Fréchet differentiable on L2[0，1]and（I◦K）′（v）=KTKv for all v∈L2[0，1].

Proof.（i）For any given w∈C[0，1]，we define

Then

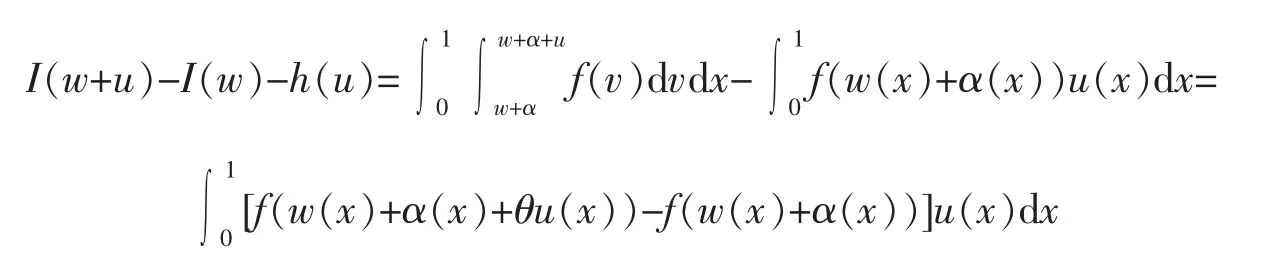
where θ∈（0，1）.Since f is continuous on[－||w+α||C-1，||w+α||C+1]，we have

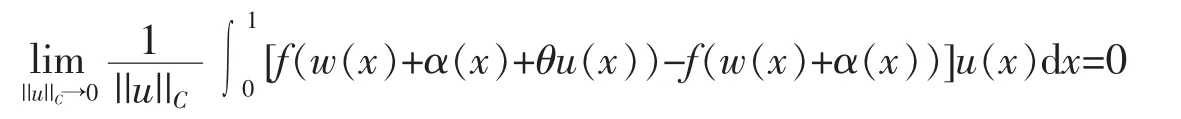
Then，I is Fréchet differentiable on C[0，1]and I′（w）u=（Tw，u）for all u，w∈C[0，1].

（ii）By the chain rule for derivatives of composite operator and Lemma 1（ii），it is obvious that the conclusion holds.

Let us introduce a functional J：L2[0，1]→Ras

Then，according to Lemma 2，J∈C1（L2[0，1]，R）and

It follows from Lemma 1 that Problem（2）has a solution in C4[0，1]if and only if the functional J has a nontrivial critical point in L2[0，1].More precisely，if v∈L2[0，1]is a critical point of J，then u=Kv+α is a solution of Problem（2）in C4[0，1].Thus Problem（2）has a variational structure.

3 Proof of main result

Now we are going to prove our main result.Our main tool is a general variational principle of Ricceri（see[13，Theorem 2.5]），which we recall here，stated in the most suitable form for our purposes.

Lemma 3Let X be a reflexive real Banach space，and let Φ，Ψ：X→Rbe two sequentially weakly lower semicontinuous and Gâteaux differentiable functionals.Assume also that Φ is strongly continuous and coercive.For every r>infXΦ，set

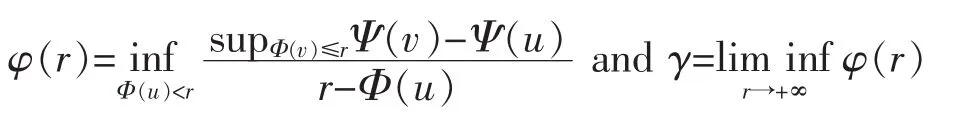
Then，the following conclusions holds：

If γ<+∞，then for every λ∈（0，1/γ）（λ∈（0，+∞）if γ=0），either

（A1）Φ-λΨ possesses a global minimum；or

（A2）there exists a sequence{un}of critical points of the functional Φ-λΨ such that

thus the energy functional becomes J（v）=Φ（v）-λΨ（v）.Then we only need to prove that Φ（v）-λΨ（v）has infinitely many critical points in L2[0，1].

It is obvious that Φ and Ψ are Gâteaux differentiable and sequentially weakly lower semi-continuous.Obviously，Φ is strong continuous and coercive.

In our case，we can define the function φ of Lemma 3 by putting for every r>0

Proof of Theorem 1For every v∈L2[0，1]，Φ and Ψ are defined by

We claim that

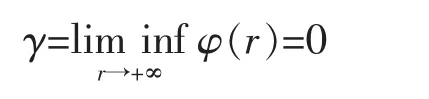
Clearly， γ≥0.On the other hand，by（F1），we can deduce that there is a sequence{cn}in（0，+∞）with cn→+∞such that

Let rn=8cn2so that rn→+∞.By using inequalities（4），then for every u∈L2[0，1]with Φ（u）≤rn，we have

Take v0（x）=0 for all x∈[0，1]，then||v0||=0<2rn，it follows from（7）that

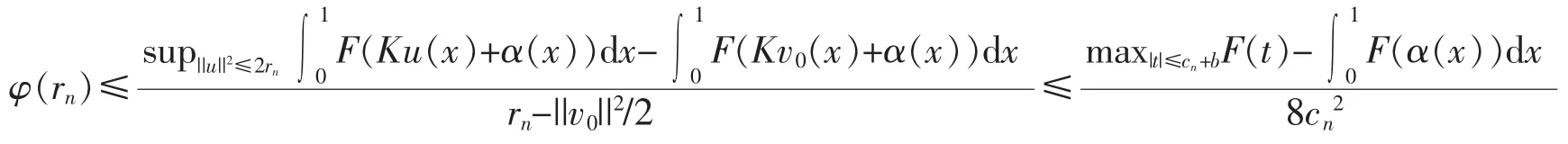
Since cn→+∞，there exists N∈Nsuch that

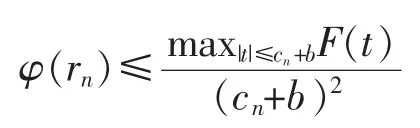
for all n>N.This，together with（6），implies

Then γ=0.

In the sequel，we will show that

Indeed，Let wn（x）=π2（bn-b）sinπx for all x∈[0，1].It follows from Remark 1（b）that

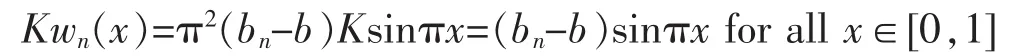
By an

Thanks to（F2），F（s）is nonincreasing for s∈（an，bn）.Thus，according to（F1）and（8），we have

Therefore，for n∈N，

Take η=sup{ηn}.If B1<+∞，let λ＞π4/4B1（1-2η）and ∈∈（π4/4λB1（1-2η），1），then by（F2）there exists N∈∈N such that

for all n＞N∈.Note that the choose of∈，it follows from（9）that for all n＞N∈，

Therefore，the （A1）in Lemma 3 can be excluded.Thus，（A2）holds，i.e.for every λ>λ*=π4/4B1（1-2η），there exists

a sequence{vn}of critical points of J=Φ-λΨ such that

If B1=+∞，let M>π4/4λ（1-2η），then by（F2）there exists NM∈Nsuch that

for all n＞NM.This yields that for all n＞NM，

so that

Then，（A2）of Lemma 3 holds for any λ>0，that is，for every λ>0，Problem（2）has infinitely many solutions in C4[0，1].This concludes the proof.