基于切片二维图像的血管三维重建研究
2018-09-20靳瀛王敬前
靳瀛,王敬前*
(1.陕西服装工程学院经济管理学院,陕西西安,712046;2.陕西服装工程学院基础部,陕西西安,712046)
引言
三维重建是指用切片机连续不断地将样本切成数十、数百的平行切片,依次逐片观察后,根据拍照并采样得到的平行切片数字图像,运用计算机来重建组织、器官等准确的三维形态。本文是基于切片二维图像的血管三维重建研究,主要目的是为了得出三维图像。现着重解决以下问题:
问题1,研究如何求出血管半径的方法,并求出血管管道半径。
问题2,根据问题1研究求管道的中轴线的计算方法,并求出管道中轴线的数学模型函数关系式。
问题3,根据问题1、问题2研究如何绘制管道的中轴线分别在XY,YZ,ZX平面的投影图,再根据这些平面投影图研究如何绘出制血管管道的三维立体图像。
1 问题分析
根据题中所给的图片立体想象出血管的应动情况,本文的难点是由于血管不是类似于圆柱体的有规则图形,而是一个无规则图形,为了计算更精准,在计算血管半径时利用每一张切片的内切圆求平均值。
1.1 问题1分析
首先,根据题中给出的信息,将第一张切片导入MATLAB软件,利用矩阵的形式表达出第一张切片骨架和轮廓;接着,利用MATLAB软件编程求出第一张切片骨架中到轮廓上所有点之间的最短距离,在这些最短距离中取最大距离为即为第一张切片的半径;最后,按照求第一张切片的半径的方法,分别求出 100张切片的半径,利用平均值公式求得这100个切片半径的平均值,这个平均值就是血管管道的半径大小
1.2 问题2分析
首先,通过问题1模型的建立和求解,得出100张切片内切圆的圆心坐标,将这些坐标导入Excel表格中,通过MATLAB软件对坐标进行处理得出一个散点图;然后,根据这个散点图拟合出多个函数图象,将这些函数图像做比较从中挑出最优函数,挑出的最优函数为三角函数;最后,得出管道中轴线的数学模型函数关系式为:
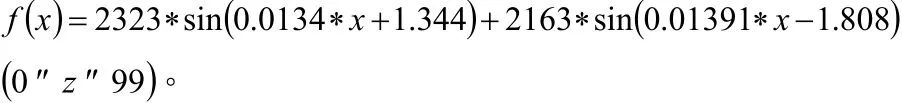
1.3 问题3分析
首先,通过问题1模型的建立和求解,得出100张切片内切圆的圆心坐标,将这些坐标导入Excel表格中,利用MATLAB软件绘制管道的中轴线分别在XY,YZ,ZX平面的拟合函数图形;然后,通过MATLAB软件编程得到管道的中轴线分别在XY,YZ,ZX平面的投影图;最后,绘制出血管管道三维重建的三维立体图像。
2 模型的建立与求解
2.1 问题1的解决方案
首先,将图中所给的第一张切片导入MATLAB软件中;然后,利用MATLAB软件编程求出第一张切片的半径;接着,按照求第一张切片方法接的剩余99张切片半径;最后,求出100张切片半径的平均值,这个平均值即为血管管道半径。
2.1.1 问题1模型的建立
对题中所给信息进行分析,由于题中所给的信息有有,为了使所求半径更接近实际值,可根据每一个切片半径来求血管管道的半径。故本文将100个切片分开处理。
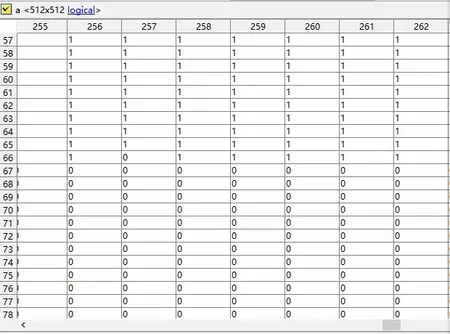
图6 转至前第一张切片的0-1矩阵局部图
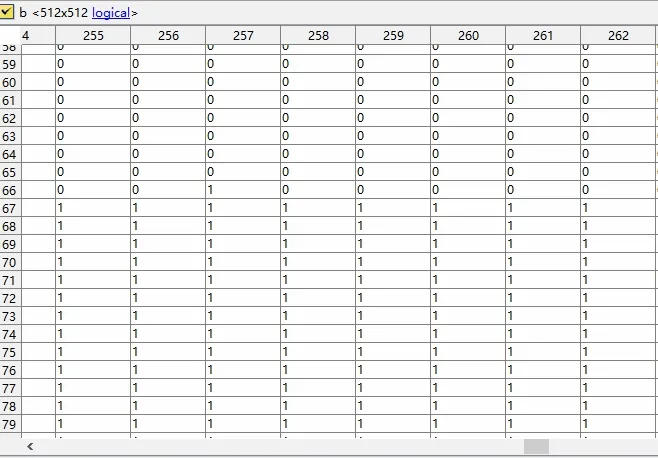
图2 转至后第一张切片的0-1矩阵局部图
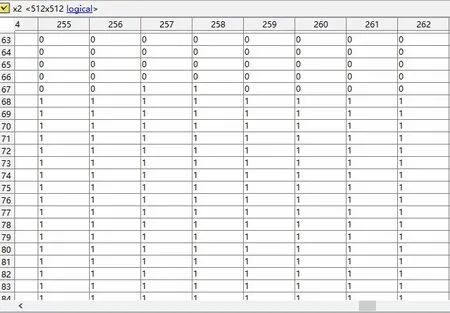
图3 第一张切片骨架的0-1矩阵局部图
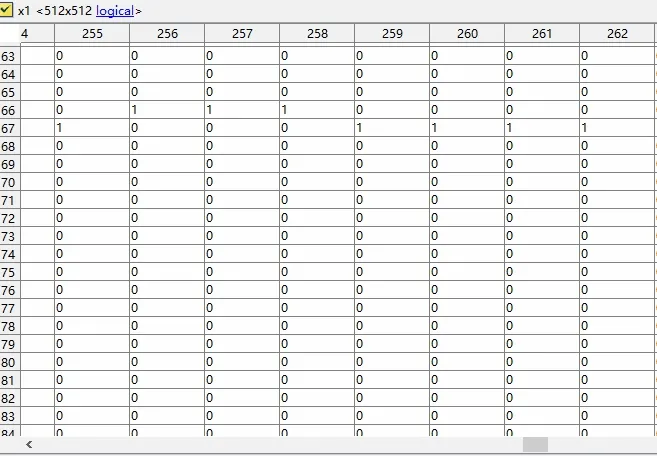
图4 第一张切片轮廓的0-1矩阵局部图
图3,图4是分别从第一张切片的骨架和轮廓矩阵中提取第226至292列与第67至124行的数据。
两点之间距离公式为:

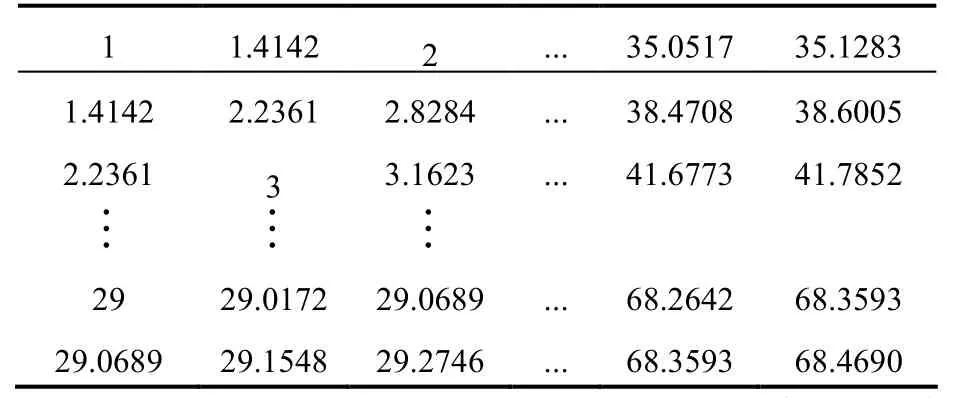
表1 第一张切片骨架中所有点到轮廓上所有点的距离排序

表2 第一张切片骨架任一点到轮廓所有点最短距离
根据表2,选出最短距离中的最大距离,作为第一张切片的半径大小
接着,按照上述方法分别求出剩余的99张切片的半径,在解得切片半径的同时可以利用MATLAB软件得出切片内切圆的圆心坐标。

表3 100张切片半径及最大内切圆圆心坐标

36 30.672 -152 55 35 37 30.169 -152 58 36 38 30.372 -152 58 37 39 29.884 -152 58 38 40 31.067 -148 58 39 41 30.000 -149 68 40 42 30.537 -140 66 41 43 29.378 -140 84 42 44 29.811 -135 84 43 45 30.666 -135 92 44 46 29.431 -135 92 45 47 29.87 -115 92 46 48 30.625 -113 116 47 49 30.987 -112 118 48 50 30.654 -111 119 49 51 30.481 -111 120 50 52 29.004 -111 120 51 53 29.545 -111 120 52 54 29.389 -111 120 53 55 30.267 -66 120 54 56 30.555 -59 150 55 57 30.192 -70 153 56 58 30.437 -70 148 57 59 30.271 -54 148 58 60 30.482 -54 155 59 61 30.194 -31 155 60 62 29.529 -31 162 61 63 29.651 -6 162 62 64 29.097 -6 166 63 65 30.037 8 166 64 66 30.109 10 167 65 67 29.207 11 167 66 68 29.803 12 167 67 69 29.176 12 167 68 70 30.290 12 167 69 71 30.145 26 167 70 72 29.086 26 166 71 73 30.047 46 166 72 74 29.167 65 163 73 75 29.012 65 158 74 76 29.034 71 158 75 77 29.006 96 156 76 78 30.291 96 145 77 79 30.249 127 145 78 80 29.001 127 124 79 81 30.111 122 124 80
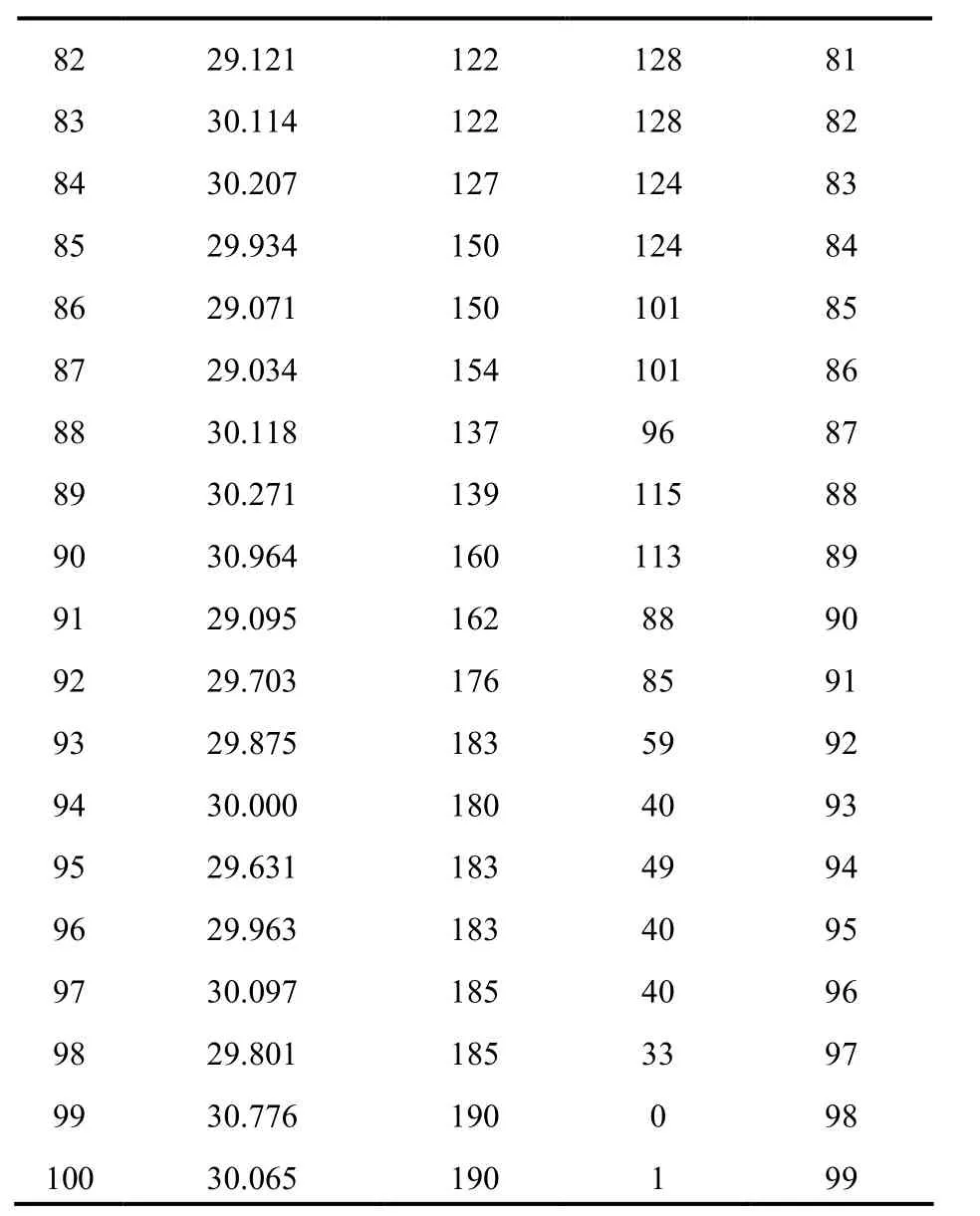
82 29.121 122 128 81 83 30.114 122 128 82 84 30.207 127 124 83 85 29.934 150 124 84 86 29.071 150 101 85 87 29.034 154 101 86 88 30.118 137 96 87 89 30.271 139 115 88 90 30.964 160 113 89 91 29.095 162 88 90 92 29.703 176 85 91 93 29.875 183 59 92 94 30.000 180 40 93 95 29.631 183 49 94 96 29.963 183 40 95 97 30.097 185 40 96 98 29.801 185 33 97 99 30.776 190 0 98 100 30.065 190 1 99
最后,为了使得血管管道半径更加精确,应求出这100个半径的平均值。平均值计算公式如下:

将100 张切片的半径代入公式2中,求出100个半径的平均值大小
2.1.2 问题1模型建立的步骤
综上所述,问题一的具体实现步骤可以总有如下:

输入:相继100张平行切片图像输出:最大内切圆半径步骤:(1)导入管道的相继100张平行切片图像,获取图像的像素矩阵;(2)对图像的像素矩阵进行0-1转换;(3)获取转化后图像的像素矩阵的轮廓和骨架,并返回轮廓和骨架坐标;(4)求得出切片骨架中一点 512 Xi 到轮廓上所有点 512 i 1…Yj 之间的最小距离;(5)求所有最小距离中的最大值;(6)返回最大值。j 1…
2.2 问题2的解决方案
首先,在问题1模型的建立和求解的同时得出100张切片内切圆的圆心坐标;然后,将这些坐标导入Excel中,通过MATLAB软件拟合出曲线图;最后,得到管道中轴线的数学模型函数关系式。
2.2.1 问题2模型的建立
首先,对表3进行观察发现,在问题一模型的建立与求解中已经得出100张切片内切圆圆心坐标。
其次,将这些坐标导入Excel表格中,通过MATLAB软件对坐标进行处理得出一个散点图,并根据这个散点图拟合出多个函数图象。图5、图6、图7是拟合得出最接近散点图的指数函数和三角函数图像。经过对上图的观察,图7最接近散点图,所以我们选取三角函数为最优函数。
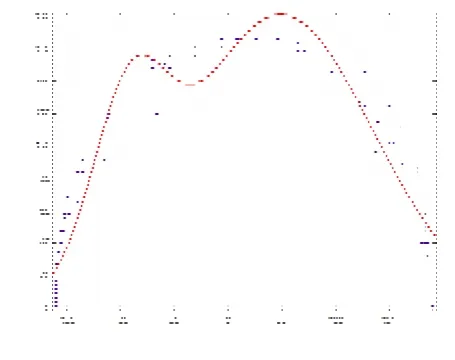
图5 指数函数图像

图6 指数函数图像
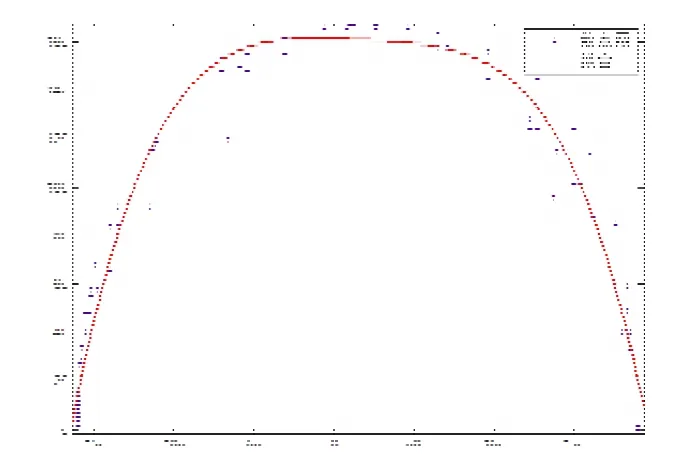
图7 三角函数图像
最后,根据散点图拟合得到的三角函数数学模型中的三角函数关系式

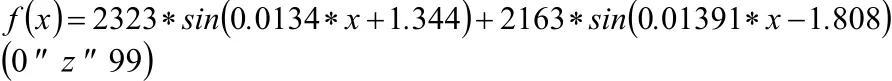
2.3 问题3的解决方案
要求绘制管道的中轴线分别在XY,YZ,ZX平面的投影图。首先,在问题1模型的建立和求解的同时得出100张切片内切圆的圆心坐标,将这些坐标导入Excel中,绘制管道的中轴线分别在XY,YZ,ZX平面的拟合函数图形;然后,再通过编程得到分别在XY,YZ,ZX平面投影图;最后,绘制血管管道的三维立体图像。
2.3.1 问题3模型的建立
首先,将表3中 100张切片的内切圆圆心坐标导入Excel表格中,利用 MATLAB软件绘制管道的中轴线分别在XY、YZ、ZX平面的拟合函数图形,再通过MATLAB软件编程得到分别在XY、YZ、ZX平面投影图。图8至图13分别为XY、YZ、XZ的平面的散点图和拟合函数图以及中轴线在XY、YZ、XZ平面的投影图,再根据这些图得到三维立体图像。
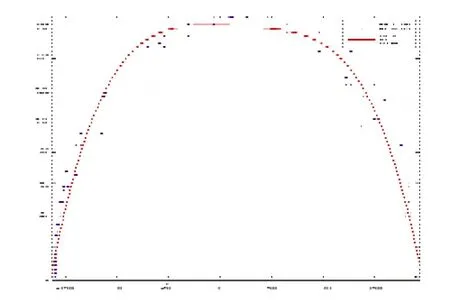
图8 XY平面的散点图及拟合函数图
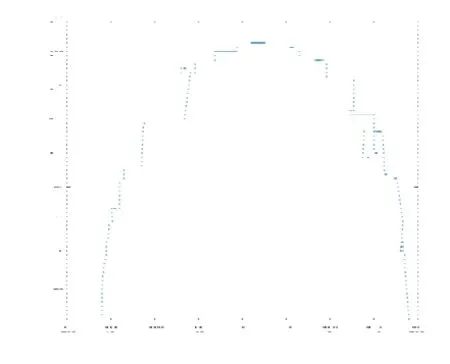
图9 中轴线在XY平面的投影图
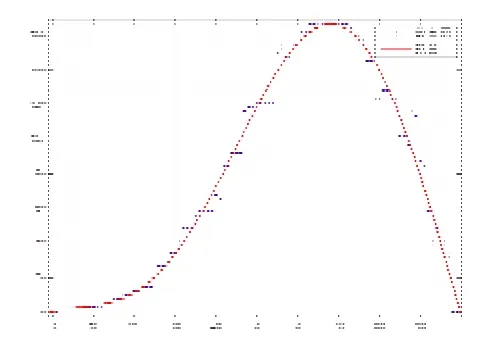
图10 YZ平面的散点图及拟合函数图
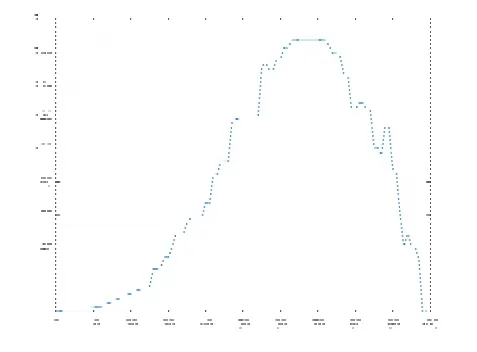
图11 中轴线在YZ平面的投影图
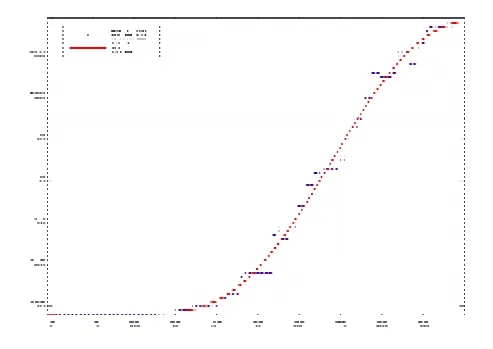
图12 XZ平面的散点图及拟合函数图

图13 中轴线在XZ平面的投影图
图14即为本文所求的血管三维重建的三维立体图形
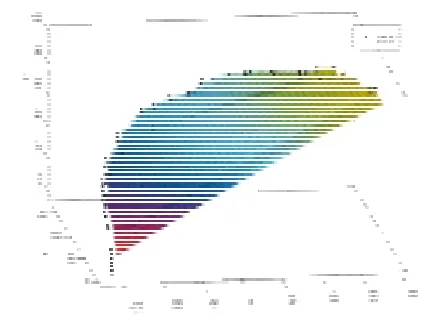
图14 血管管道的三维立体实体
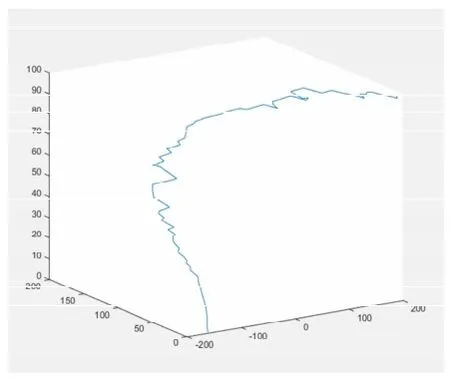
图15 血管管道的三维立体散点
3 有束语
(1)本文使用MATLAB软件编程建立模型,利用了平均值求解,平均值的计算能直观的反映数据的基本特征,使得到的有有精确度更高。
(2)在求管道中轴线的函数表达式时,利用多个拟合函数进行对比,最后选取最优函数,使得所得有有更加精准。
(3)模型可操作性强,适用范围广泛,不仅可以运用在血管三维重建中,还可以运用在科技[3],医学,生物体的三维重建研究中。
