圆不锈钢管混凝土曲杆受压力学性能研究
2018-09-18郑莲琼魏常贵郑永乾
郑莲琼,魏常贵,陈 敏,郑永乾
(1. 福建工程学院 土木工程学院,福建 福州 350118;2. 福建省土木工程新技术与信息化重点实验室,福建 福州 350118)
曲线形钢管结构在大跨度空间结构、桥梁结构中得到了广泛的应用,经济效益和建筑效果良好[1].图1是曲线形钢管构件在体育馆中的应用.若采用不锈钢管代替普通碳素钢管,并在曲线形空不锈钢管内浇筑混凝土形成曲线形不锈钢管混凝土构件(以下简称不锈钢管混凝土曲杆),预期与钢管混凝土直构件类似,由于不锈钢管和混凝土在受力过程中的相互作用,具有良好的力学性能,而且其外表美观、耐久性好、维护费用低.
以往国内外对直线形的钢管混凝土构件(为和曲杆对应,本文暂称之为直杆)已进行过大量研究,并有专门的设计规程[2].近年来,不锈钢管混凝土直杆也已得到一定的研究,Young和Ellobody[3]、Lam 和 Gardner[4]、Uy 等[5]对不锈钢管混凝土短柱和长柱的轴压及压弯性能进行系列试验研究,廖飞宇[6]、Tao等[7]分别对圆形和方形截面的不锈钢管混凝土轴压力学性能进行了数值分析,Chen 等[8-9]对方形、矩形和圆形截面不锈钢管混凝土构件及空不锈钢管对比构件的受弯性能进行了系统的试验研究,马国梁[10]、Tam等[11]进行了不锈钢管再生混凝土力学性能研究.
由于不锈钢和普通钢材在材料性能上存在明显差异,曲杆和直杆的失效机理也有所不同,因此有必要进一步研究不锈钢管混凝土曲杆的力学性能.为此,本文首先进行不锈钢管混凝土曲杆受压力学性能试验研究,并基于ABAQUS有限元平台建立该类构件的非线性有限元分析模型,在计算结果得到试验结果验证的基础上,基于数值分析模型,研究不锈钢管混凝土曲杆受压工作机理,最后,对不锈钢管混凝土曲杆受压承载力计算方法进行探讨.

图1 曲线形构件的工程应用Fig.1 Curved members used in a space structure
1 试验研究1.1 试验概况
进行了12个不锈钢管混凝土曲杆的试验研究,试件的截面形式均为圆形(以下简称圆不锈钢管混凝土曲杆),不锈钢管均采用φ101×1.64,轴线均采用目前钢管拱桁架工程中较常见的圆弧形.试验还设计了3个不锈钢管直杆和1个空不锈钢管曲杆对比试件.如图2(a)所示,对曲杆进行两端截面中心受竖向压力试验,以下简称轴压曲杆,其初始弯曲度为u0(曲杆中截面的形心到构件两端截面形心连线的垂直距离);如图2(b)所示,对直杆进行偏心受压试验,以下简称偏压直杆,荷载偏心距为e(e与对应曲杆的u0相同).
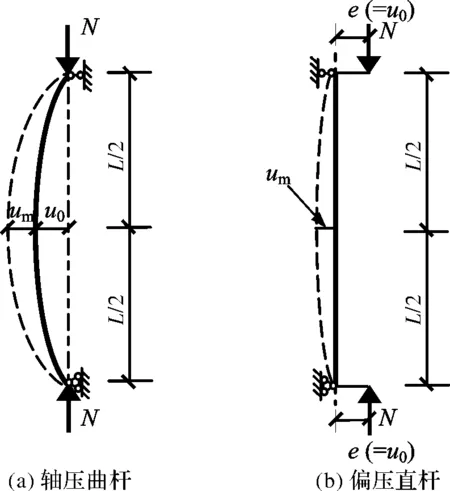
图2 不锈钢管混凝土构件挠曲变形示意图Fig.2 A general view of member deflection curves
试验的主要参数为曲杆的曲度系数(βr)和名义长细比(λn),βr和λn定义如下:
βr=u0/L
(1)
λn=L/i
(2)
式中:L为构件弦长,即构件两端截面中心之间的直线距离;i为构件截面的回转半径,本文试验构件为圆形截面,λn=4L/D;D为试件外直径.
表1给出了试件编号及试件的详细设计参数,其中,σ0.2为不锈钢实测名义屈服强度(残余应变为0.2%时的应力),Nue为试件承载力实测值,Nuc为按有限元法计算所得的试件承载力值,NDBJ为采用福建省地方标准《钢管混凝土结构技术规程》DBJ/T 13-51-2010[12]提供的钢管混凝土压弯构件承载力公式等效计算得到的试件承载力值.表1中的试件编号首字母L1、L2和L3用以区分不同的名义长细比;第二个数字0、1、2和3用以区分不同曲杆的初始弯曲度或直杆的荷载偏心距;第三个字母C代表轴压曲杆,S代表偏压直杆,K代表空不锈钢管.
制作试件时首先截取出长度合适的直不锈钢管(AISI 304),慢速拉弯达到设计曲度的圆弧形.不锈钢管混凝土中核心混凝土采用自密实混凝土,配合比为:水190 kg/m3;普通硅酸盐水泥320 kg/m3;II级粉煤灰180 kg/m3;砂850 kg/m3;碎石960 kg/m3;HSC聚羧酸高性能减水剂的掺量为0.5%.混凝土浇筑时实测其坍落度为260 mm,流动扩展度为610 mm.28 d和试验时实测的混凝土立方体抗压强度分别为35.4 MPa和46.5 MPa,试验时混凝土弹性模量Ec为3.31×104MPa.不锈钢材料性能从弯曲后的不锈钢管取出标准试件,经拉伸实验测定,不同弯曲度的不锈钢管名义屈服强度略有差异,其值列于表1,而不锈钢管的弹性模量Es和泊松比μs随试件弯曲度的变化差别不大,实测Es的平均值为1.95×105MPa,μs平均值为0.289.
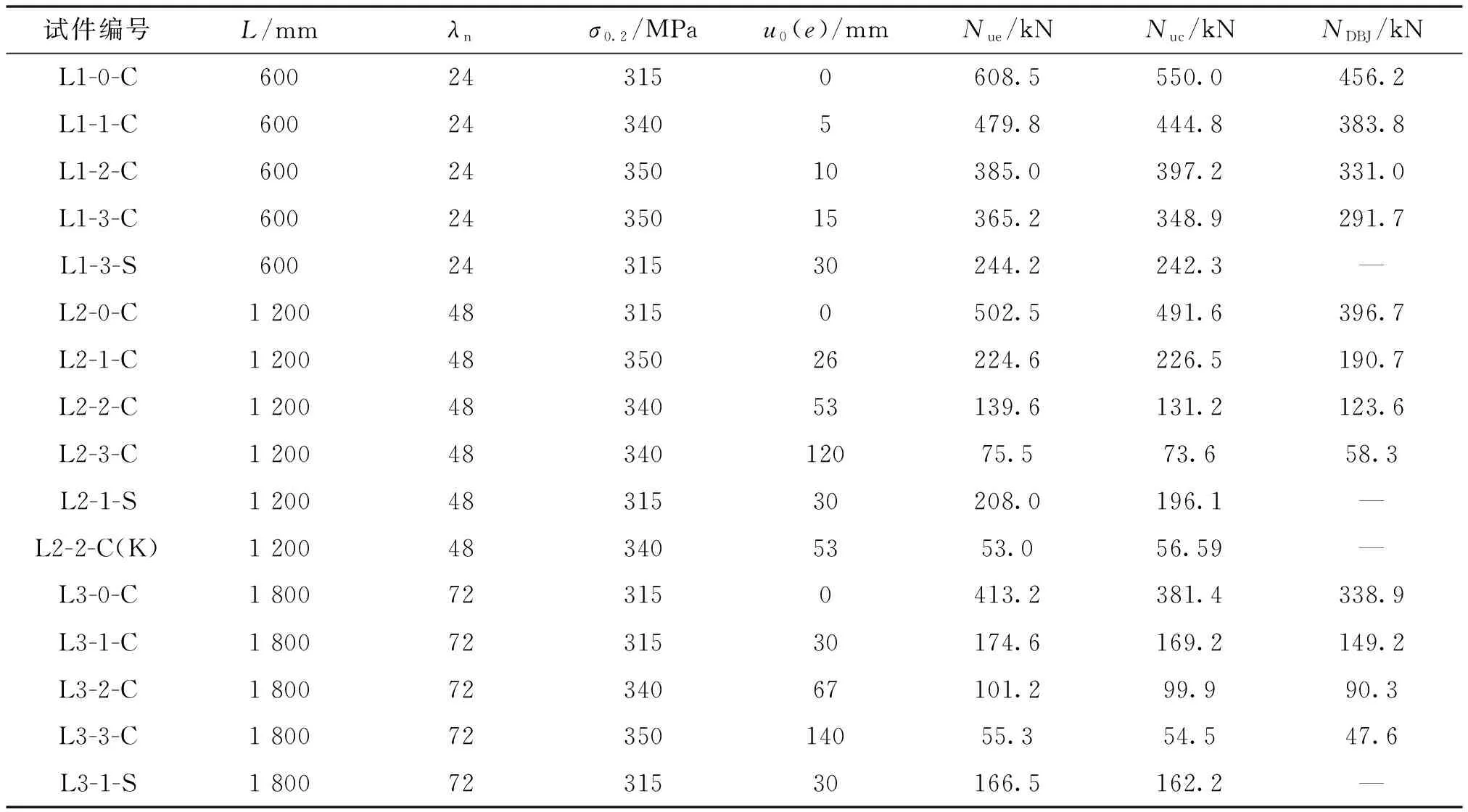
表1 试件参数
试验在500T压力机上进行,试验装置和测点布置如图3所示,为了实现铰接边界条件,在试件两端各设置一套特制刀铰和加载板.加载板上按一定间距设有多条6 mm深V形凹槽,曲杆试件加载时,刀绞对准加载板中心的凹槽,竖向压力通过试件两端截面的形心;偏心受压直杆加载时,刀绞对准加载板相应偏心距的凹槽.
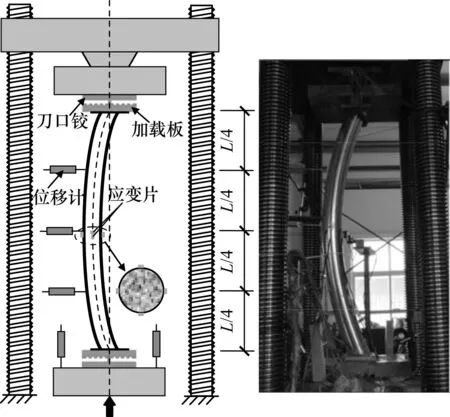
图3 曲线试验加载装置Fig.3 Test setup of curved specimens
试验采取分级单调加载.弹性范围内每级荷载约为估算极限荷载值的1/10,每一级荷载的持荷时间为1~2 min,加载至不锈钢管压区纤维达到屈服点后,改为位移加载,位移加载速度为0.5 mm/min.同时连续记录各级荷载所对应的变形值,直至试件承载力下降到极限荷载的60%或侧向变形量达40/L时停止试验.
整个试验过程中荷载、位移和应变均采用IMC数据采集系统自动采集.在每个试件跨中截面外表面每隔90°设置纵向和环向各一的共八片电阻应变片.同时,在试件弯曲平面内沿构件高度四分点处设置三个位移计以测定试件的面内侧向挠度发展,在试件弯曲平面外中截面处设置一个位移计以测定试件的面外侧向挠度变化,在试件端部设置两个对称的位移计以监测试件的纵向总变形.
1.2 试验结果分析
1.2.1 试件破坏形态
图4所示为试验结束后试件的破坏形态(不同名义长细比的试件破坏形态相近,限于篇幅未给出λn=72试件的破坏形态),可以看出,不锈钢管混凝土轴压曲杆和偏压直杆的破坏形态类似,这是由于曲杆在端部中心轴竖向荷载作用下,沿试件轴线各截面均承受轴力和弯矩的共同作用,与偏压时的工作机理类似.
对试件加载过程中的挠曲变形观测表明,试件随荷载增加在弯曲平面内的挠度不断增大.在初始加载阶段,试件挠曲变形发展较慢,跨中挠度的增长基本上和荷载的增加成正比.当荷载达到极限荷载的60%~70%时,跨中挠度开始明显增加,二阶效应的影响趋于明显.在峰值荷载前,未见不锈钢管局部变形,进入下降段后期,所有试件均在跨中截面附近出现了不同程度的不锈钢管鼓曲.进一步移除曲杆跨中压区不锈钢管,如图5所示,名义长细比较小的试件跨中截面混凝土被压碎,其他部位混凝土没有开裂破坏,名义长细比较大的试件其核心混凝土无明显被压碎现象.
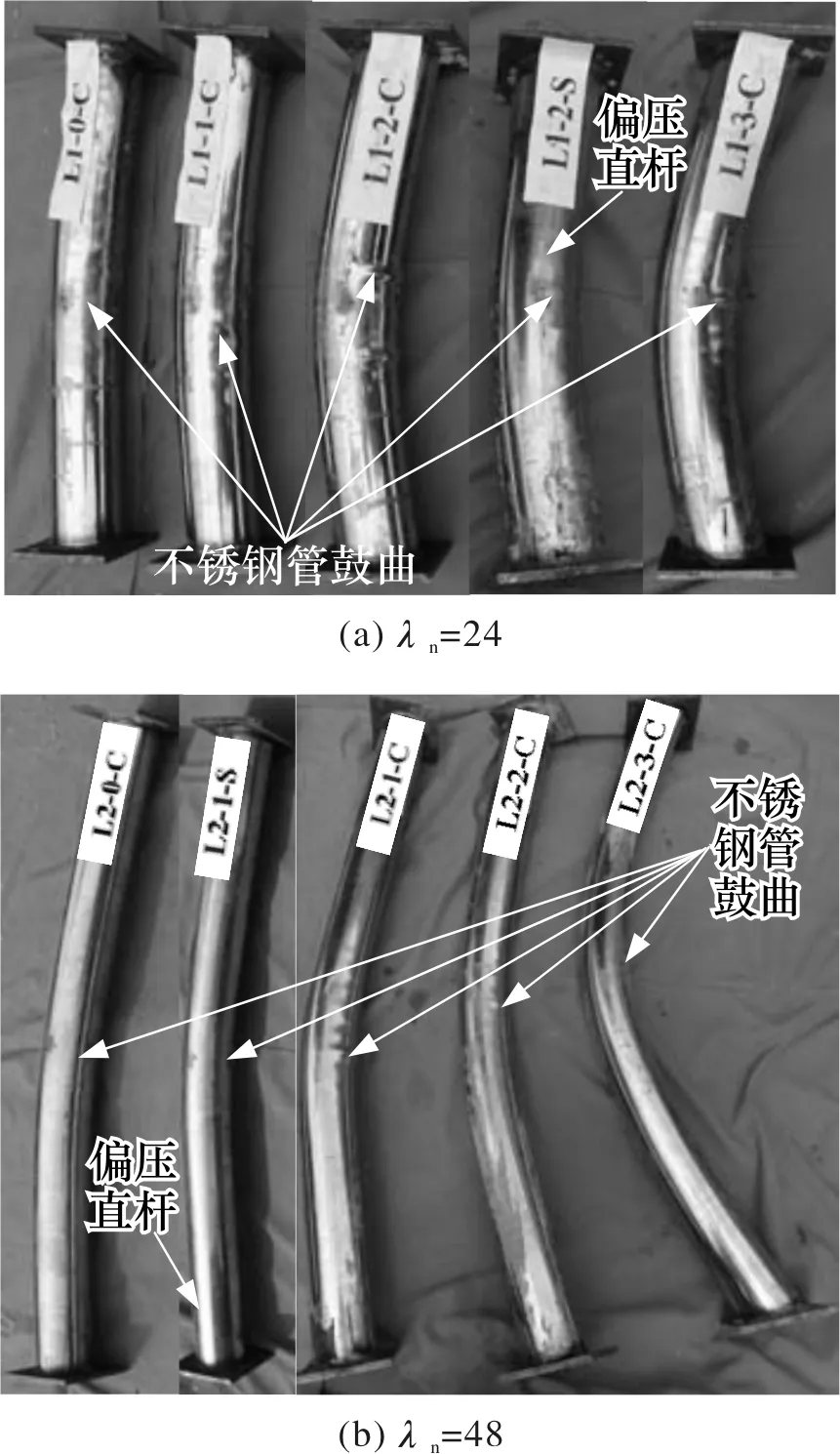
图4 试件最终破坏形态Fig.4 Failure modes of all testing specimens
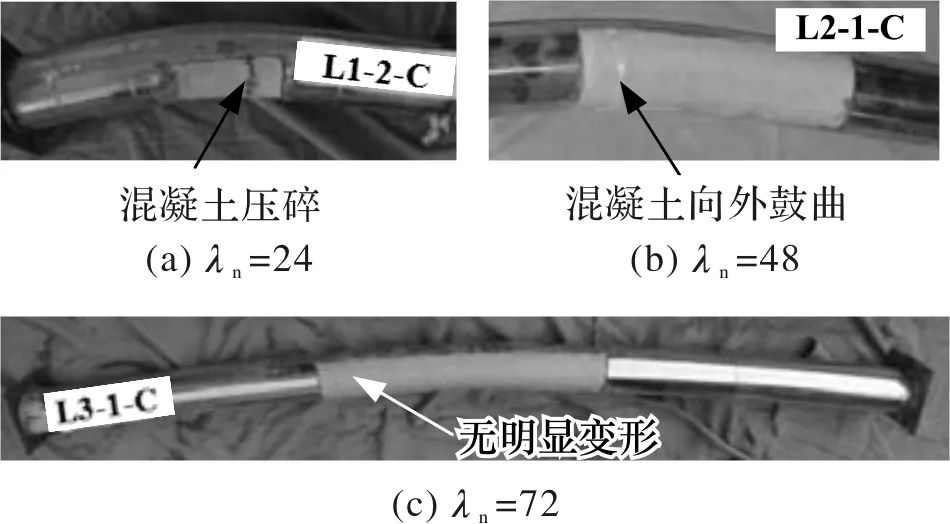
图5 试件核心混凝土破坏形态Fig.5 Failure modes of core concrete
图6给出了空不锈钢管曲杆与不锈钢管混凝土曲杆破坏形态的对比,可以看出,空不锈钢管混凝土曲杆由于没有核心混凝土的支撑,试件的延性和整体变形能力较差,在跨中受压侧发生明显的内凹屈曲后承载力迅速下降,随后凹曲急剧增加,表现出明显的局部破坏和脆性破坏的特点.

图6 核心混凝土对破坏形态的影响Fig.6 Failure modes of specimens with or without concrete
图7绘出了本次试验的一组轴压曲杆和偏压直杆对比试件在不同荷载作用阶段其挠曲变形的发展情况,其中纵坐标为试件上的测点距试件底部的距离,横坐标为加载过程中试件不同位置处的挠度,Nu为试件的极限荷载.
图7中同时给出了跨中挠度相同的正弦半波曲线.由图7a可见,在达到极限荷载前,轴压曲杆的挠曲线与正弦半波曲线较为吻合,但在加载后期,挠曲线形状与正弦半波曲线稍有差别,具体表现为试件两端的挠度发展稍慢于正弦半波曲线.此外,曲杆在达到极限荷载时的跨中侧向变形也略小于相应的偏心受压直杆.
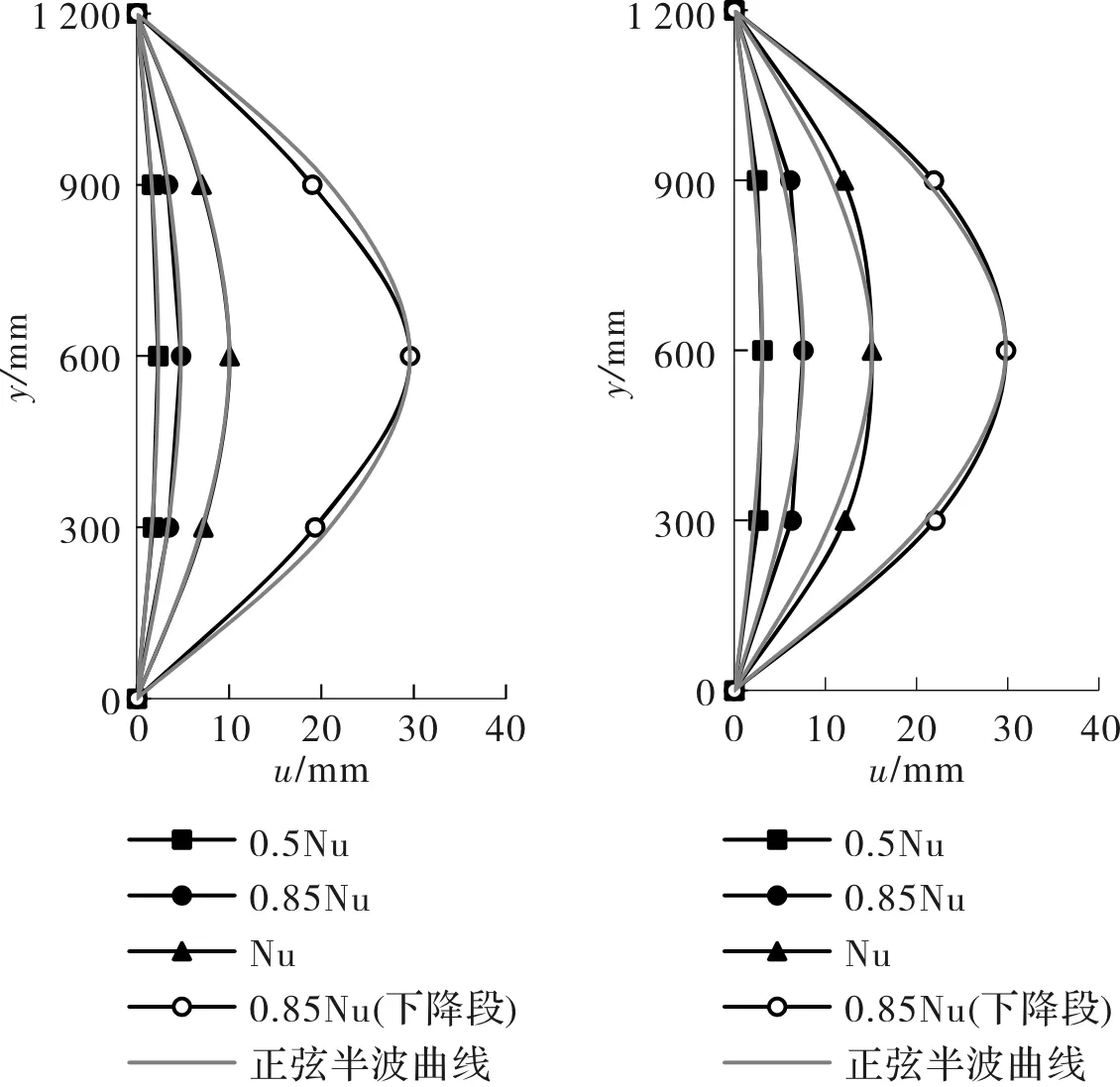
图7 轴压曲杆和偏压直杆试件的挠曲变形发展情况Fig.7 Lateral deflection of specimens during test
1.2.2 荷载-跨中挠度关系曲线
图8给出不锈钢管混凝土曲杆实测的荷载(N)与跨中挠度(um)关系曲线,试件的峰值荷载Nue汇总于表1.从图8可以看出,随着试件名义长细比(λn)和跨中初弯曲(u0)的增大,轴压不锈钢管混凝土曲杆的初始刚度减小,极限承载也随之降低,达到峰值荷载时对应的跨中挠度相应增加.而随着λn或u0的增大,试件N-um曲线的下降段更为平缓.
图9给出了空不锈钢管曲杆的N-um关系曲线,实验结果表明,在空不锈钢管曲杆内填充混凝土明显提高了试件的承载能力、刚度和延性.
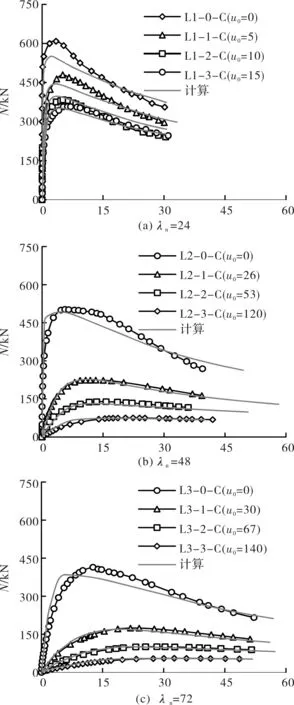
图8 不锈钢管混凝土曲杆荷载(N)-跨中挠度(um)关系曲线Fig.8 Load (N) versus lateral deflection (um) curves of curved concrete-filled stainless steel tubular specimens
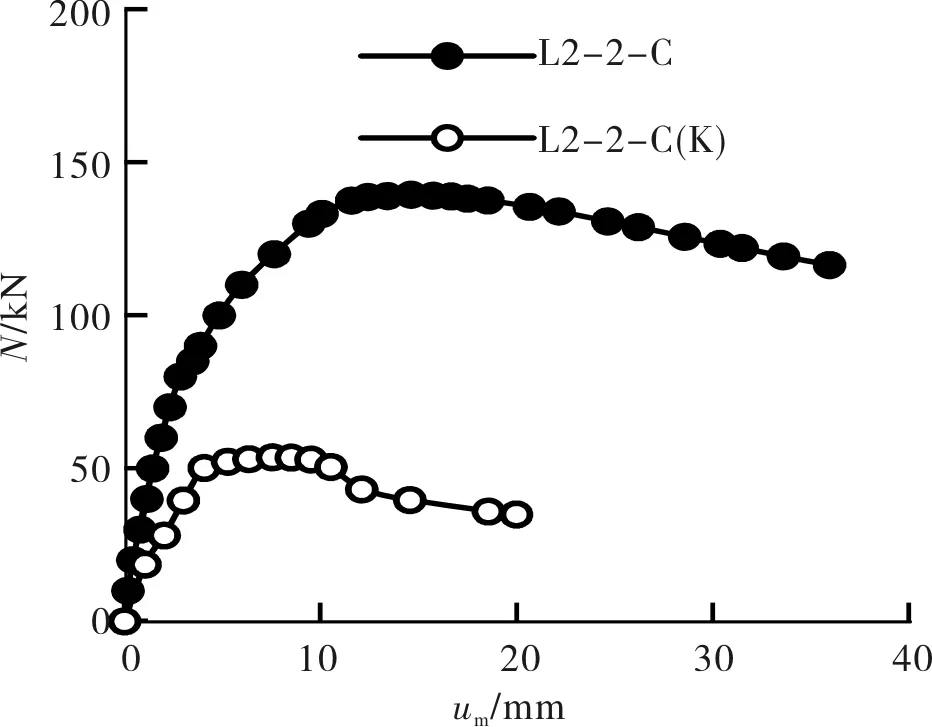
图9 填充混凝土对曲杆荷载-跨中挠度关系曲线影响Fig.9 N versus um curves of specimens with or without concrete
图10所示为不锈钢管混凝土轴压曲杆与对应的偏压直杆N-um关系曲线对比,由于λn=24的曲杆试件加工误差,其跨中初弯曲远小于对应的偏压直杆的荷载偏心距,故图10中不进行比较.由图10可见,轴心受压曲杆和偏心受压直杆的N-um关系曲线发展规律基本一致,曲线进入弹塑性段后,曲杆的刚度和承载力要略高于直杆,这是由于初弯曲和初偏心构件受压时二阶效应的影响不同.本次试验λn=48和72的曲杆的Nue值比相应的直杆分别高7.98%和4.86%.

图10 轴压曲杆与偏压直杆N-um曲线比较Fig.10 Comparison of N-um curves of curved and straight specimen
1.2.3 荷载-跨中应变关系曲线
图11给出了由贴在不锈钢管壁上的应变片测得的试件跨中截面的受拉区和受压区边缘纤维处纵向应变(ε)随荷载(N)变化的关系曲线,应变值以拉为正.当βr较小时,构件在达到极限荷载前处于全截面受压状态,随着βr的增大,构件跨中截面从受力初期即分成了拉、压两个区,且压区应变的增长明显快于拉区.随着曲度系数的增加和名义长细比的减小,构件峰值荷载对应的应变增大,可见随着曲度系数的增大和长细比的减小构件变形能力更强.
图12为不锈钢管混凝土偏压直杆对比试件N-ε关系曲线,可以看出,在同一荷载水平下,偏压直杆的压应变略高于轴压曲杆,从微观应变验证了偏压直杆的“二阶效应”比相应的轴压曲杆更明显一些,因此偏压直杆的极限承载力比轴压曲杆稍低.
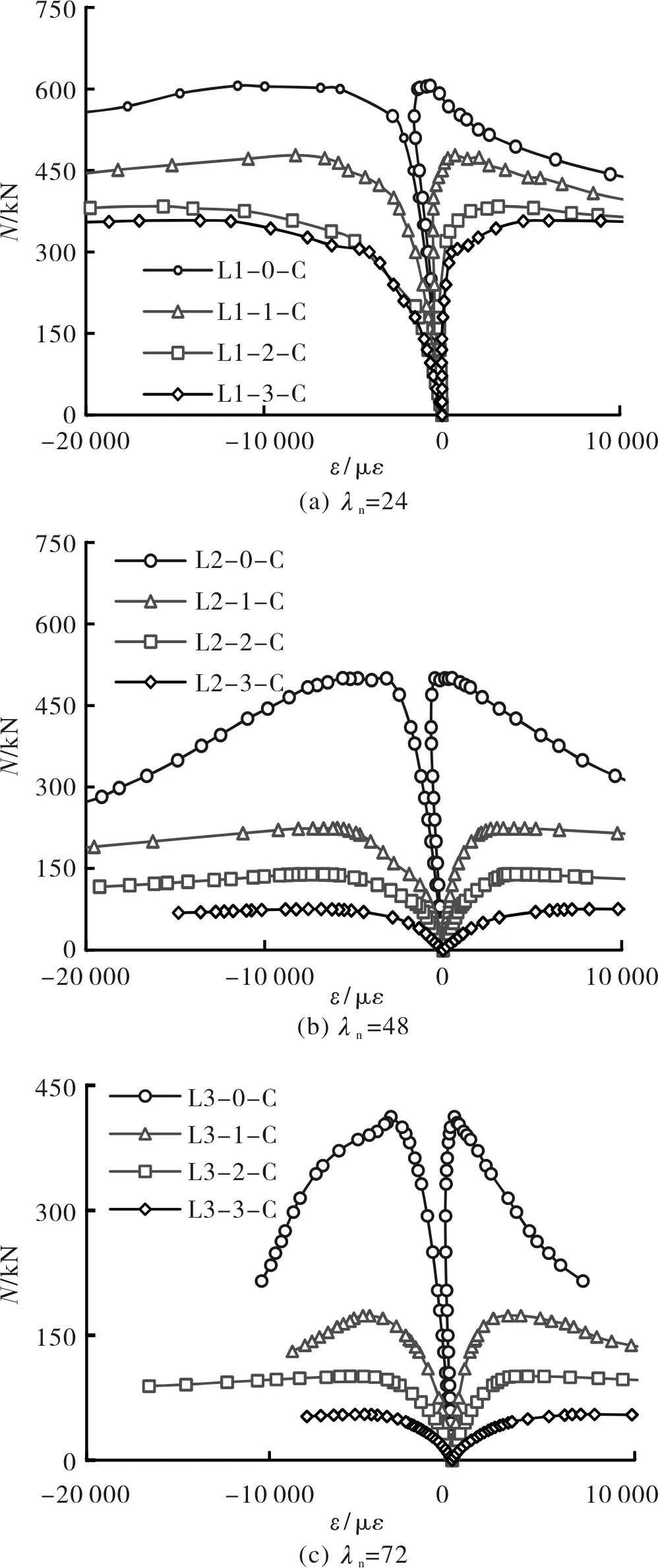
图11 典型的荷载(N) -跨中应变 (ε) 关系曲线Fig.11 Load (N) versus fibre strains (ε) at mid-height
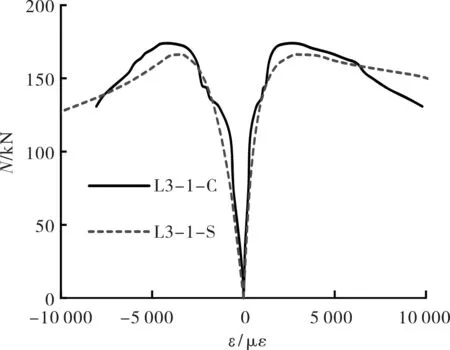
图12 轴压曲杆与偏压直杆N-ε关系曲线对比Fig.12 Load (N) versus fibre strains (ε) at mid-height
2 理论分析
2.1 模型的建立和验证
建立几何模型时,首先定义不锈钢管和核心混凝土的初始弯曲曲线作为“sweep”路径,然后定义不锈钢管和混凝土的截面尺寸,截面将沿着初始弯曲曲线扫掠形成不锈钢管混凝土曲杆几何模型,如图13所示.
不锈钢采用各向同性弹塑性模型[13],其单轴σ-ε关系采用欧洲规范[14]建议的公式,受压情况下的n取4.3[15].混凝土采用塑性损伤模型,廖飞宇[6]在计算不锈钢管混凝土构件时核心混凝土单轴受压的等效应力-应变关系采用与普通碳素钢约束混凝土相同的模型,取得了良好的效果,本文暂采用该模型,单轴受拉采用应力-断裂能模型.
不锈钢管采用四节点壳单元(S4R),核心混凝土采用八节点三维实体单元(C3D8R).与碳素钢管混凝土类似,不锈钢管与核心混凝土的界面法向采用“硬接触”,切向采用库伦摩擦模型,不锈钢与混凝土的摩擦系数取0.25[6].如图13所示,不锈钢管混凝土构件的边界条件为对一端端板截面几何中心加载线约束X、Y、Z方向位移,另一端板上截面几何中心加载线上约束Y、Z方向位移,为获得下降段,采用位移加载,在截面几何中心上加X方向位移.
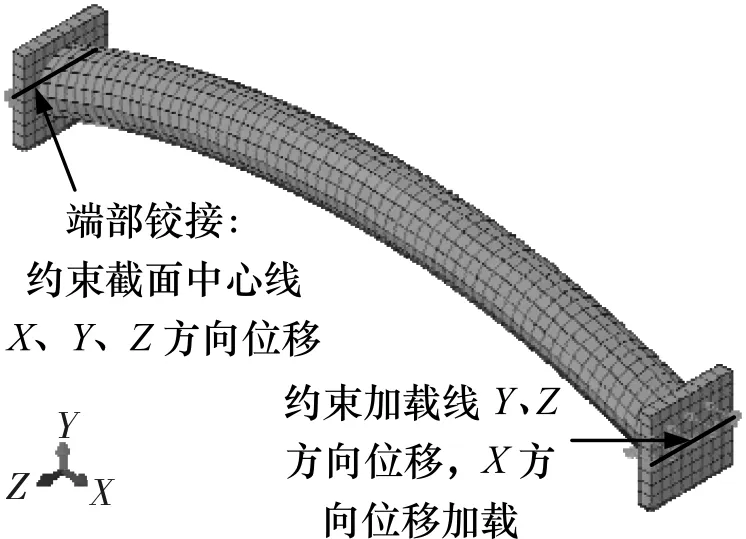
图13 有限元模型Fig.13 Finite element model
为验证上述所建模型分析结果的准确性,对本文进行的试验结果进行了对比计算,计算得到的荷载-跨中挠度全过程曲线如图8灰色实线所示,计算得到的试件极限承载力(Nuc)列于表1.图14给出了本文试验试件及Uy等[5]进行的圆截面轴心受压中长柱极限承载力计算值与实验值的比值(Nuc/Nue),对文献[5]算例计算时取L/1 000的初偏心.所有试件Nuc/Nue的平均值为0.942,均方差为0.099.可见,理论计算的极限承载力和实测结果较为吻合.

图14 极限承载力计算结果(Nuc)与试验结果(Nuc)对比Fig.14 Comparison of ultimate load between numerical results and tested results
2.2 受力特性分析
采用建立的有限元模型,通过典型算例分析不锈钢管混凝土曲杆的受力特性,算例的基本参数为:D=400 mm,t=9.31 mm,L=4 000 mm,βr=2.5% (u0=100 mm),σ0.2(fy)=345 MPa,fcu=60 MPa.
2.2.1 荷载-变形关系
图15所示为计算的轴心受压不锈钢管混凝土曲杆及其不锈钢管、核心混凝土各自的N-um关系曲线.可以看出,不锈钢管混凝土曲杆尚未达到其极限承载力时,不锈钢管承担的荷载就已达到峰值,其荷载-变形关系开始进入下降段;而核心混凝土位于截面核心,且受到不锈钢管的约束作用,因而不锈钢管达到极限承载力时其分担的荷载仍能继续增加,使得组合构件的N-um关系曲线仍然保持上升的趋势,直至核心混凝土也达到其极限承载力,N-um关系曲线才开始进入下降段.
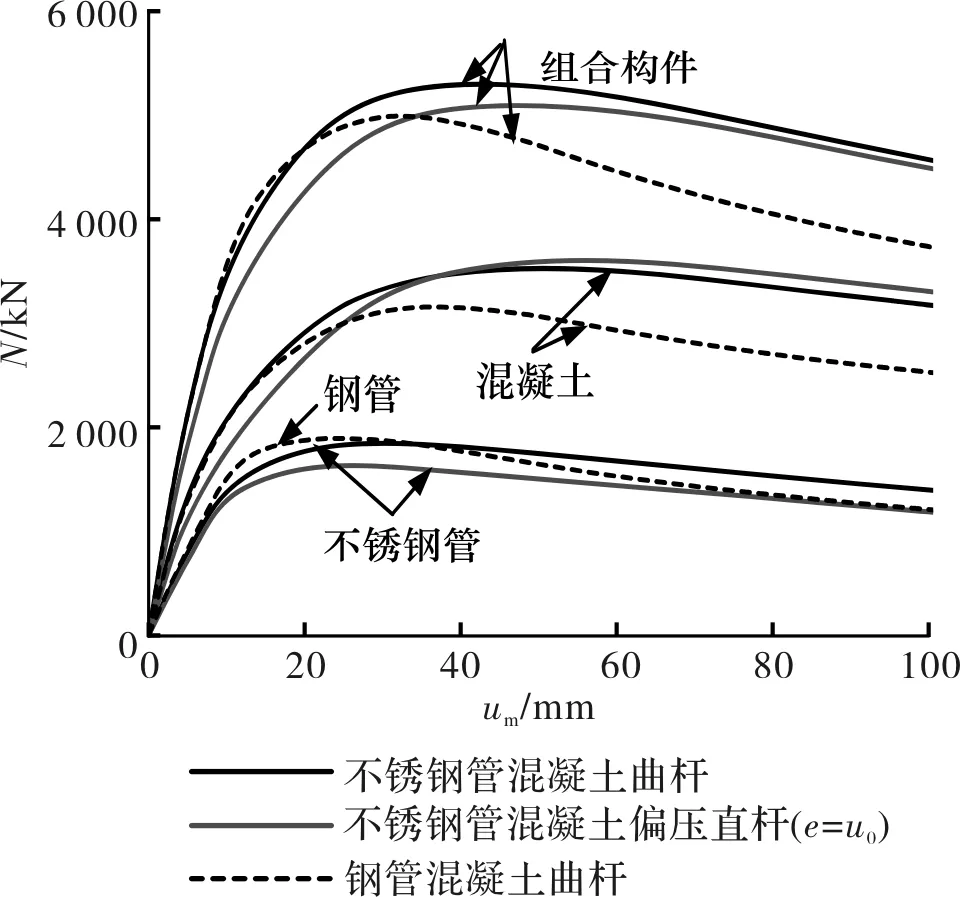
图15 N-um关系曲线比较 (u0/L=1/40)Fig.15 Predicted N versus um curves (u0/L=1/40)
为比较分析,图15中同时给出了钢管混凝土曲杆、不锈钢管混凝土偏压直杆及其(不锈)钢管、混凝土各自的N-um关系曲线.可以看出,三类构件的极限承载能力及N-um曲线发展相近.与钢管混凝土曲杆相比,不锈钢管混凝土曲杆由于不锈钢在加载初期就表现出明显的非线性特征,构件进入弹塑性段后,不锈钢管混凝土曲杆刚度较钢管混凝土曲杆低约5%,而不锈钢后期显著的应变强化性能给核心混凝土提供更强的约束作用,使得核心混凝土承担更大的荷载,从而不锈钢管混凝土曲杆极限承载力较钢管混凝土曲杆高约6%,且峰值点后前者的曲线下降更为平缓,表现出更好的延性.
不锈钢管混凝土曲杆的极限承载力为5 299.6 kN,较相应的偏压直杆高4%,初始刚度高约14%~18%.可见,曲杆中“二阶效应”对弯矩和挠度的放大作用均小于相应的偏压直杆.两类构件中不锈钢管承担的荷载接近,而偏压直杆由于更大的二阶弯矩使得受拉退出工作的核心混凝土面积更大,因此,混凝土承担的荷载较相应的曲杆小.
2.2.2 应力和应变分析
图16给出轴心受压不锈钢管混凝土曲杆与对应的不锈钢管混凝土偏压直杆的荷载(N)-不锈钢管边缘纤维纵向应变(ε)关系曲线.可以看出不锈钢管混凝土曲杆的边缘纤维应变发展与偏压直杆相近,在受压区,二阶弯矩产生的附加压应力由不锈钢管和混凝土共同承担,偏压直杆受压边缘不锈钢管压应变几乎与轴压曲杆重合;而在受拉区,混凝土退出工作,同一荷载水平下,轴压曲杆不锈钢受拉应变小于偏压直杆,二者差值在10%~20%之间.在偏压直杆接近峰值荷载时,应变迅速发展,荷载峰值点(N=5 097 kN)不锈钢最大受拉纵向应变为3 293 με,相同荷载下,轴压曲杆中不锈钢最大受拉纵向应变为1 778 με.

图16 不锈钢管混凝土构件N-ε关系曲线比较 (u0/L=1/40)Fig.16 Predicted N versus ε curves of concrete-filled stainless steel members (u0/L=1/40)
图17给出了轴心受压不锈钢钢管混凝土曲杆与偏心受压不锈钢管混凝土直杆达峰值荷载时中截面处核心混凝土的纵向应力分布对比.可见,轴压曲杆和偏压直杆的中截面应力分布规律基本一致.图中同时标示出了构件中和轴的位置,可以看出,轴压曲杆达峰值荷载时中截面受压面积稍大,因此轴心受压曲杆承载力略大于偏心受压直杆.
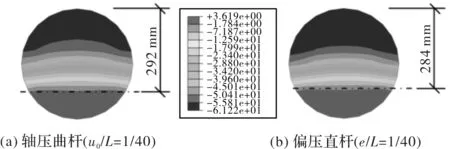
图17 极限承载力时中截面混凝土纵向应力分布Fig.17 Longitudinal stresses in the mid-height of core concrete
2.2.3 不锈钢管和混凝土相互作用
图18给出了不锈钢管混凝土轴压曲杆和相应的偏压直杆在加载过程中不锈钢管对核心混凝土的约束力(p)变化情况,图中Nu为构件的峰值荷载.可见,不锈钢管对混凝土产生约束作用的区域主要集中在跨中附近L/4的范围内.在不锈钢管屈服点,两类构件中约束力分布有很大区别,但此时约束力数值较小,对构件性能没有明显影响;在荷载峰值点,不锈钢管混凝土轴压曲杆跨中附近拉、压两侧不锈钢管对核心混凝土均有较强的约束作用,而偏压直杆中约束作用发展主要在受压侧;进入下降段,两类构件中的约束作用又趋于相同.
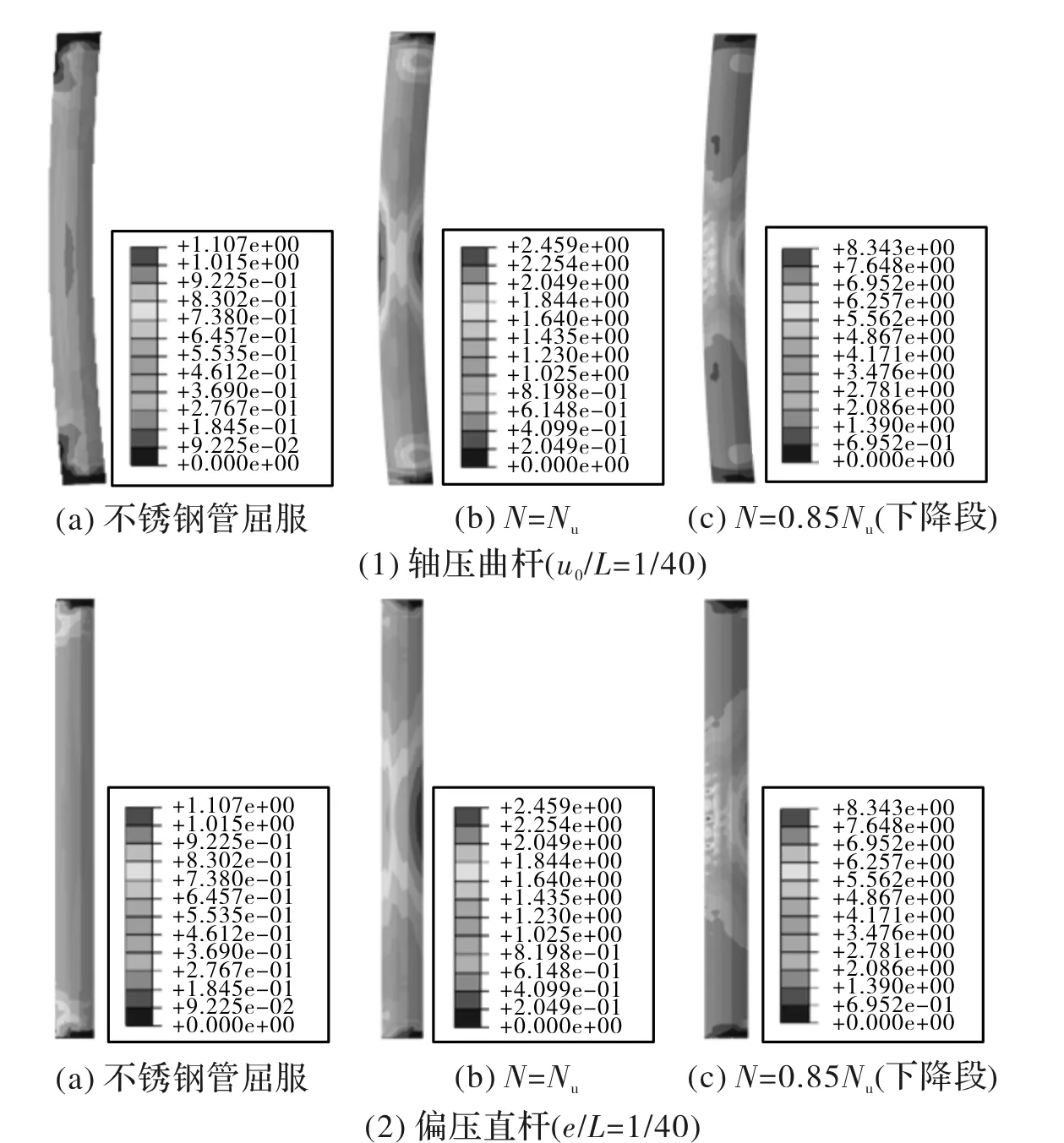
图18 不锈钢管混凝土构件约束作用发展Fig.18 Distribution of contact stresses
3 参数分析与承载力计算
根据以上对不锈钢管混凝土曲杆进行的试验研究和数值分析可以看出,不锈钢管混凝土曲杆由于存在初始弯曲,当在构件两端截面的形心施加竖向压力时,构件将受到弯矩和轴力的共同作用,其受力性能和不锈钢管混凝土偏压直杆的受力性能总体上类似,但不锈钢管混凝土曲杆承载力略高于相应的偏压直杆.为定量分析两类构件的承载力差别,定义二者的承载力系数如下:
SI=NucC/NucS
(3)
式中,NucC为计算得到的不锈钢管混凝土曲杆受压承载力,NucS为相应的不锈钢管混凝土偏压直杆承载力.
选取与受力特性分析相同的典型算例,变化其中一个参数,保持其他参数不变,考察曲度系数(βr)、名义长细比(λn)、不锈钢强度(σ0.2)、截面含钢率(α,截面不锈钢管面积与核心混凝土面积的比值)和混凝土强度(fcu)对SI的影响规律,计算结果如图19所示.二者差异的程度随试件曲度系数、不锈钢强度、截面含钢率的增大而增大,随着混凝土强度的增大而减少,而随着名义长细比的增大,二者的差值先减少后增大,在本文分析的参数范围内,SI值均在1.05以内.因此,为简化两端截面中心受压不锈钢管混凝土曲杆的设计,其承载力计算可按对应的偏心受压不锈钢管混凝土直杆进行计算,计算时取偏心距等于曲杆的初始弯曲度.
不锈钢管混凝土构件作为新型组合构件,目前尚未有规程提供其承载力计算方法.UY B等[5]计算对比发现,福建省地方标准《钢管混凝土结构技术规程》DBJ/T 13-51-2010[12]对不锈钢管压弯构件的承载力计算值与实验值最为接近.采用该规程提供的压弯构件承载力公式,取M=N·u0,对本文试验的不锈钢管混凝土曲杆受压承载力进行计算,计算结果如表1中NDBJ所示,NDBJ/Nue的平均值和均方差分别为0.828和0.044.因此,暂可以采用该规程的方法偏于安全地计算不锈钢管混凝土曲杆受压承载力.
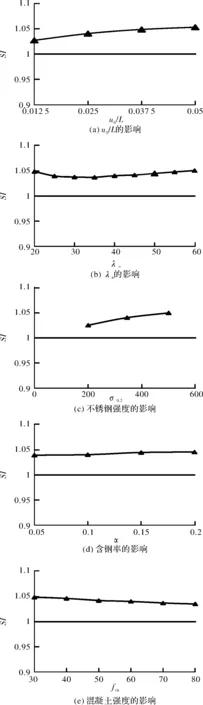
图19 各参数对SI的影响Fig.19 The effects of each parameter on SI
4 结论
本文对不锈钢管混凝土曲杆在两端截面形心施加竖向压力作用下的力学性能进行了试验及计算方法研究,得到以下几点结论:
(1) 不锈钢管混凝土曲杆具有良好的承载能力和抗变形能力.随着名义长细比或初始弯曲度的增大,不锈钢管混凝土曲杆的初始刚度减小,极限承载力也随之降低.不锈钢管混凝土曲杆的承载力和刚度均略高于相应的偏压直杆.
(2) 采用有限元法对不锈钢管混凝土曲杆受压荷载-变形全曲线、应力应变发展及不锈钢管与核心混凝土约束作用等进行了分析,计算结果与实验结果吻合良好.
(3) 不锈钢管混凝土曲杆受压承载力较相应的偏压直杆提高值在5%以内,采用规范DBJ/T 13-51-2010[12]计算普通钢管混凝土直构件压弯承载力的公式可偏于安全地应用于不锈钢管混凝土曲杆设计.
