基于事件驱动的容积卡尔曼滤波定位算法
2018-09-18,,,*
,,,*
1.火箭军工程大学,西安 710025 2.火箭军驻7103厂军事代表室,西安 710100
网络化控制系统(Networked Control System, NCS)凭借其分布式和模块化的特点在传感器网络、微机电系统以及多智能体控制等领域得到广泛的应用[1]。网络化状态估计系统(Networked State Estimation System, NSES)作为NCS的重点技术组成之一,凭借其传感器和估计器通过无线网络连接的优势,极大地增加了传感器的监测范围,因此该技术被广泛应用于目标跟踪定位、工业设备的状态监控以及搜救危险区域等领域[2]。
NSES中负责感知探测的传感器和负责滤波计算的估计器往往分布在不同的空间领域,因此存在以下问题:
1)传输网络的不稳定性和传输环境的复杂性往往会导致量测信息的丢失和延迟。
2)传感器每次向估计器传输量测信息都要消耗一定的能量,然而传感器往往携带的能量有限。
3)在传感器较多的网络化滤波系统中,信道资源有限,限制了传感器向估计器传输量测信息。
国内外众多学者对NSES中的通信问题进行了研究,文献[3-8]对系统中的数据丢包问题展开了深入研究,文献[9]进一步在数据丢包的基础上进一步研究了信息传输延时问题。文献[6]和文献[8]均通过独立同分布的Bernoulli过程描述了NSES中的丢包问题,文献[8]重点分析了固定丢包概率对系统稳定性的影响,而文献[6]则在最小均方误差条件下推导了次优估值器(包括滤波、平滑和预报)。文献[9]则设计了线性最小方差意义下的最优线性估计器,并给出了稳态估计器存在的充分条件。为研究信息丢失率对滤波性能的影响,文献[10]给出了滤波器收敛的临界丢包条件。
上述文献均采用随机过程来描述NSES中的数据被动丢包过程,但为了在有限的通信资源条件下达到最佳的估计性能,一种基于事件驱动的思想在NSES中成为了当前研究的热点[11-12]。文献[13]证明了相比于传统的等间隔采样方式,基于事件驱动的采样方式能有效降低系统输出的方差。文献[14]提出了基于随机事件驱动的网络化状态估计技术,主要研究了线性系统主动舍弃量测信息条件下的卡尔曼滤波方法。文献[15]研究了在NCS中如何设计基于事件驱动的控制方法,设计了一种基于连续观测自身状态变化率的事件驱动模式。文献[16]则设计了一种基于当前真实状态和估计状态差值的自发事件驱动模式。因此,在事件驱动问题的研究中,如何设计“最优”的事件是关键问题之一。
上述研究大多是基于线性系统的,而对非线性系统的研究通常基于EKF算法进行简单的线性化处理,EKF算法的核心是通过泰勒展开的方式进行线性化处理,因此通常存在求雅克比矩阵过程过于复杂和舍弃误差较高的问题[17],不适用于高维度的强非线性系统。
容积卡尔曼滤波(CKF)方法是一种新兴的非线性滤波器,CKF通过容积积分规则对Bayes框架下的预测和更新公式进行数值近似,文献[18]将CKF与传统的扩展卡尔曼滤波(Extended Kalman Filter,EKF)和无迹卡尔曼滤波(Unscented Kalman Filter,UKF)进行了比较,对其稳定性和性能进行了对比分析,证明了CKF算法在高维度强非线性的系统中效果更好。
本文的研究重点分为两个方面:一是在随机事件驱动的基础上建立了检测事件驱动模式;二是将事件驱动的思想引入CKF算法框架,推导事件驱动条件下CKF算法的更新方式。最后以天基空间目标跟踪为背景,建立高维度强非线性的跟踪系统,分析了同等通信率条件下,不同事件驱动方式下的CKF算法的性能,仿真结果表明,基于检测事件驱动的CKF算法对空间目标的跟踪性能良好,具有一定的研究意义和实用价值。
1 问题描述及预备知识
1.1 网络化状态估计系统结构
考虑如图1所示的网络化最优估计系统。该系统中传感器和估计器是分离的,传感器的信息能否成功传输到估计器取决于决策器输出的信号,信息到达与否是决定网络化滤波系统精度高低的关键因素之一。
1.2 非线性滤波系统
考虑如下非线性滤波系统:
(1)
式中:f(·)为状态的非线性函数,描述了系统状态量xk的变化过程;h(·)为量测非线性函数,由传感器的观测方式决定;vk,wk分别为量测噪声和系统噪声,且均为独立的高斯白噪声,其方差分别为Rk,Qk。
2 事件驱动建模
2.1 事件驱动的数学描述
定义1:事件驱动模型。
假设决策器中存在某种决策机制p,当满足该条件时γk=1,否则γk=0,即:
通过对变量γk的建模,可以描述不同类型的事件驱动模型。
2.2 随机事件驱动
定义2:随机事件驱动模型。
假设决策器输出的变量γk服从伯努利分布,其概率分布为p{γk=1}=λ,p{γk=0}=1-λ。λ表示驱动率,当λ=1时,量测信息能全部成功传输到估计器;而当λ=0时,所有的量测信息均不能到达估计器,通过控制λ的大小可以对传感器和估计器的通信率f进行控制。
理论上f=λ,其中f=NΔt/ttotal,N表示量测信息到达估计器的总次数,Δt表示传感器的采样间隔,ttotal表示系统工作的总时长。
此时,非线性滤波系统(1)中的量测噪声vk满足[1,14]:
(2)
式中,σ→∞,即当量测信息未到达估计器时,观测系统的观测噪声方差趋于无穷大。
随机事件驱动模型有效降低了通信率,但无法同时兼顾滤波精度,因此本文定义了新的驱动模型。当λ=1时,通信率为100%,随机事件驱动退化为传统的无驱动模式。
2.3 检测事件驱动
定义3:检测事件驱动模型。
变量γk的取值为:
式中:C为先验阈值,根据实际情况对精度需求的不同,C的取值不同。此时,非线性滤波系统(1)中的量测噪声vk仍然满足式(2)。
检测事件驱动通过计算量测数据的残差,当残差小于阈值C时,表示估计器的跟踪精度在可接受范围内,可暂时不接收新的量测数据;而当残差大于阈值C时,则表示估计器的跟踪精度已经不能满足精度要求,需要引入新的量测值对估计器进行修正。当C=0时,检测事件驱动退化为传统的无驱动模式。
通过检测事件驱动,可在满足精度要求的前提下,最大限度的降低通信率,通过调整阈值C便能达到调整精度标准和间接控制通信率的目的。
3 事件驱动条件下的CKF算法
3.1 事件驱动条件下的线性滤波器
针对如下线性系统:
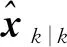
(3)
结论1:将定义1中的事件驱动模型引入线性滤波器后,当γk=1时,估计器保持原有更新过程进行预测和外推;而当γk=0时,估计器进入等待状态,其量测更新过程如式(4)所示,直至新的驱动指令到达。
(4)
3.2 事件驱动条件下的CKF算法推导
文献[19]给出了标准CKF算法的详细推导过程以及算法流程。由于引入事件驱动条件后,仅改变了其量测更新的过程,为简化表述,下面仅给出了标准CKF算法的量测更新过程:
(5)
(6)
其中预测误差协方差矩阵Pzz,k|k-1以及互协方差矩阵Pxz,k|k-1的具体求解过程如下:
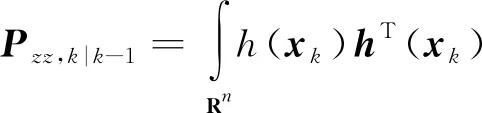
(7)
(8)
其中N(x;μ,P)表示变量x服从均值为μ协方差阵为P的正态分布,式(7)和式(8)的计算可根据容积积分规则[20]进行计算。
假设1:以CKF算法为基础,引入定义1中的事件驱动模型,估计器的量测更新过程与结论1相同。
证明:当量测值zk是否进入估计器受决策模型(4)控制时,协方差矩阵
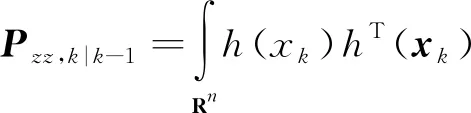
(1-γk)σ2I
(9)
(10)
状态协方差矩阵Pk|k的更新过程则可以表示为:
(11)
按照式(9)计算Pzz,k|k-1并带入式(10)和式(11)后可得到:

(12)
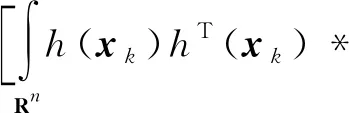
γkRk+(1-γk)σ2I]*Pxz,k|k-1
(13)
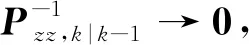
证毕。
结论2:将定义1中的事件驱动模型引入CKF算法后,当γk=1时,估计器根据标准CKF算法更新过程进行预测和外推;而当γk=0时,估计器进入等待状态,其量测更新过程如公式(4)所示,直至新的驱动指令到达。
3.3 事件驱动条件下的CKF算法框架设计
根据结论2,设计如图2所示的算法框架。
当图2中决策事件驱动模块根据定义2中的随机事件驱动模型进行工作时,此时算法为随机事件驱动CKF(Stochastic Event-triggered Cubature Kalman Filter, SECKF)算法;当图2中决策事件驱动模块根据定义3中的检测事件驱动模型进行工作时,此时算法转变为检测事件驱动CKF(Detected Event-triggered Cubature Kalman Filter, DECKF)算法。
4 空间目标无源定位系统
4.1 状态模型
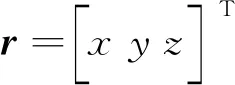
根据二体运动规律[1,21],目标的运动方程为:
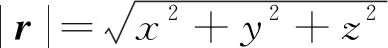
4.2 观测模型
假设高轨的观测卫星可通过光学手段获取空间目标的角度信息。目标在观测卫星轨道坐标系下测得的俯仰角βk和方位角δk定义如下[22]:
式中:φ=[φxφyφz]T为目标卫星在观测卫星质心轨道坐标系下的坐标。
定义观测量z(k)=[βkφk]T,则观测方程可表示为:
z(k)=H[x(k)]+vk
其中H(·)表示量测非线性函数。
5 仿真结果及分析
5.1 场景设定
某高轨观测卫星携带光电载荷,实时获取低轨非合作空间目标角度信息,通过将量测信息传递给计算中心实现对目标的跟踪,假设非合作空间目标为某侦察卫星。天基观测平台和非合作空间目标在任务开始时刻的轨道6要素[21]如表1所示。
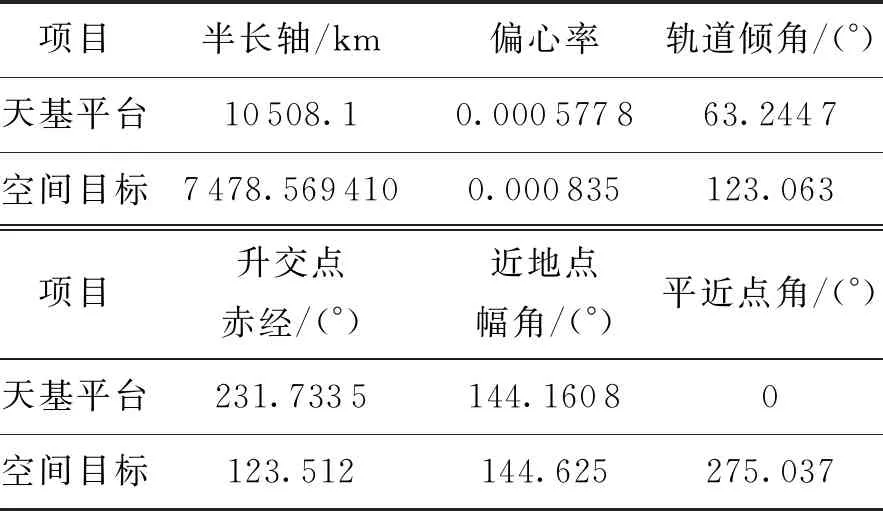
表1 平台与目标的轨道6要素
通过Matlab仿真得到空间目标与天基观测平台的星历数据,并选取连续可见时间为3 000 s的弧段进行仿真(见图 3)。
5.2 评价指标建立
为了准确描述算法的性能,便于后续算法性能的比较,建立如下比较标准。
1)均方根误差RMSE:定义一次滤波仿真试验中k时刻的均方根误差
(14)

2)位置收敛精度:以仿真最后100 s的位置均方根误差的平均值作为位置收敛精度。
3)速度收敛精度:以仿真最后100 s的速度均方根误差的平均值作为速度收敛精度。
5.3 算法参数设置
地面站对空间目标能实现高精度的定轨,但地面站的分布限制了对空间目标的观测窗口,当空间目标离开地面站的观测区域后可能存在轨道机动的行为,结合地面站的定轨精度和空间目标的机动能力,本文设定初始位置误差和初始速度误差分别为[100 100 100]Tkm、[0.1 0.10.1]Tkm/s。空间目标被动无源定位的角度测量可达到4″~7″的精度,因此假设量测噪声和系统噪声是相互独立的高斯白噪声,并假设噪声的方差为先验信息,其中方位角的方差为σβ=1mrad,俯仰角的方差为σε=1mrad。设定滤波周期T=5 s,而仿真总时长为1 500 s。
5.4 仿真结果分析
在检测事件驱动条件下,根据上述场景想定以及参数设置,采用DECKF算法对空间目标进行跟踪,当先验阈值C取8×10-6时,空间目标理论轨道和估计轨道的对比如图4所示。
可以看出DECKF算法对目标位置的估计误差逐步缩小,跟踪性能稳定。当C分别取8×10-6,5×10-7,3×10-7,0时(其中当C=0可视为传统无驱动模式下的CKF算法),进行100次蒙特卡洛仿真,计算得到不同阈值条件下的通信率f分别为0.639,0.793 6,0.873 7和1,图5为不同阈值条件下的位置和速度的均方根误差。
从图5中可以看出,DECKF算法通过检测事件驱动的形式,在有效降低通信率的同时,滤波精度损失较小,当先验阈值C取8×10-6时,DECKF算法较之传统的CKF算法虽然在跟踪精度上有所下降,但其收敛过程更为平稳,不同阈值条件下DECKF算法的具体跟踪性能如表2所示。
通过性能分析可以看出,通过调整阈值C,DECKF算法在有效降低通信率的同时能保证滤波精度维持在较高水平。当通信率损失达到20%时,算法的跟踪精度的损失在10%以内,误差的数量级未发生改变。
在同等通信率的条件下,即驱动率λ分别取0.173 9、0.793 6和0.873 7时,根据上述的场景想定以及参数设置,采用SECKF算法,进行100次蒙特卡洛仿真,并与DECKF算法进行横向对比。
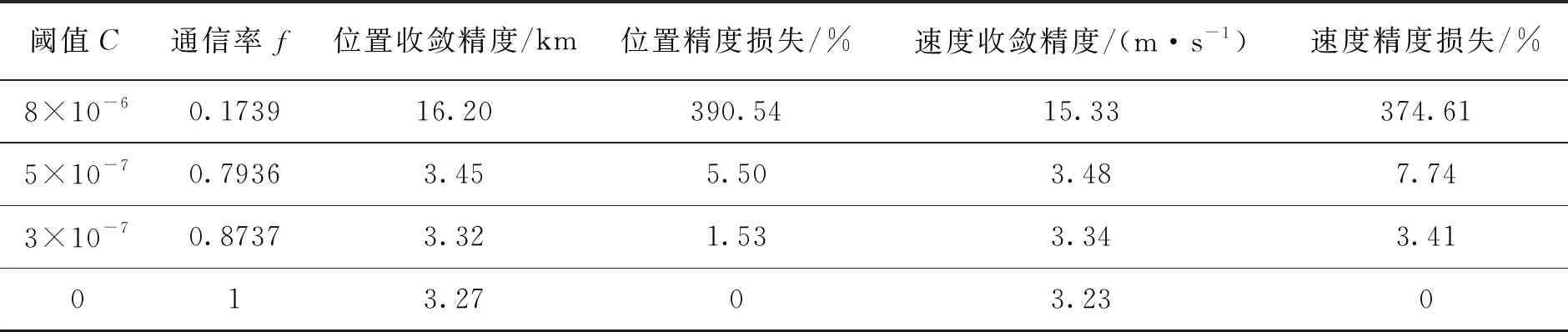
表2 不同阈值条件下DECKF算法性能比较
图6仅给出了λ=0.173 9时两种算法的性能比较结果,可以看出,在同等通信率条件下,检测事件驱动的滤波精度明显高于随机事件驱动。不同通信率条件下,DECKF算法的具体性能优势如表3、表4所示。
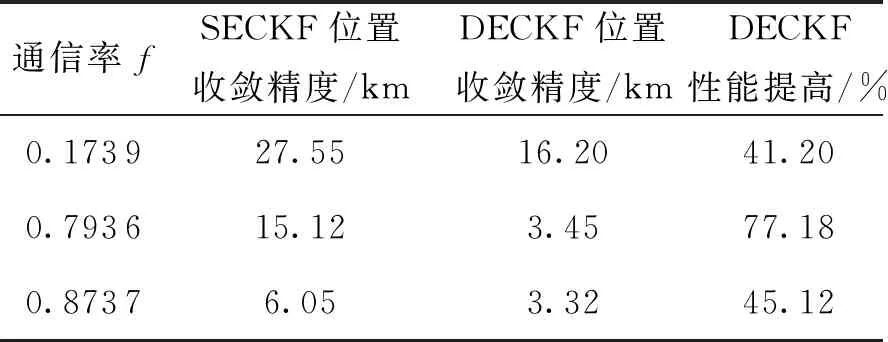
通信率fSECKF位置收敛精度/kmDECKF位置收敛精度/kmDECKF性能提高/%0.173927.5516.2041.200.793615.123.4577.180.87376.053.3245.12
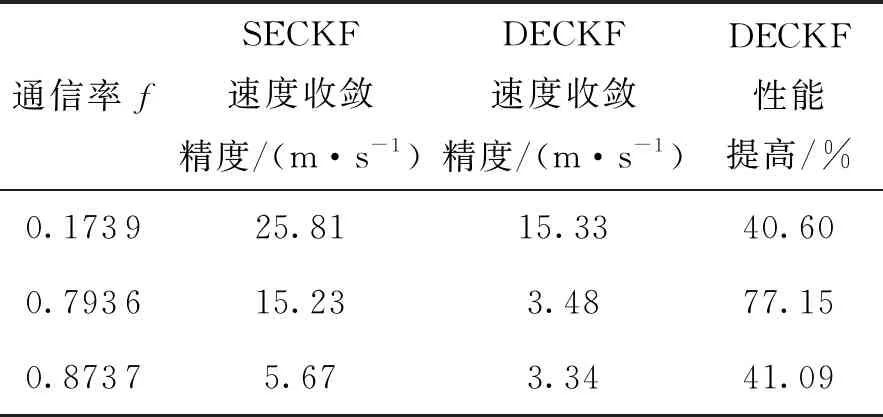
表4 DECKF与SECKF的算法速度收敛精度比较
6 结束语
以基于事件驱动的网络化非线性滤波系统为研究对象,本文的主要工作和研究结论如下:
1)为了在网络化滤波系统低通信率的条件下达到较高的跟踪精度,在随机事件驱动的基础上建立了一种基于残差检测的事件驱动模式。
2)针对非线性系统,将两种事件驱动模式引入CFK,设计了事件驱动条件下的CKF算法框架,并推导了事件驱动条件下的CKF更新过程,得到了DECKF和SECKF两种算法。
3)以天基仅测角的空间目标跟踪问题为背景,分析了不同检测阈值对DECKF算法性能的影响,通过与标准CKF的比较发现,DECKF在减少20.64%的通信率的情形下,位置跟踪精度和速度跟踪精度仅下降了5.50%和7.74%。
4)横向比较了DECKF算法与SECKF算法的性能,在同等通信率条件下,DECKF算法的滤波精度相比SECKF提高40%以上。
5)本文通过调整阈值达到了调整通信率的目的,但不能直接根据通信率的临界值设置直接指导算法的参数设置,因此如何根据通信率约束自适应的调整参数还有待于进一步的研究。
