航空发动机传感器解析余度模型的建立方法

李业波，蒋平国，田 迪，俞明帅，文彬鹤

（中国航发控制系统研究所，江苏无锡214063）

0 引言

随着航空发动机控制技术的发展，笨重的液压机械式控制系统已全面被全权限数字电子控制(Full Authority Digital Electronics Control,FADEC)系统取代[1-3]。为了满足航空发动机安全性和可靠性的要求，FADEC系统一般采用双通道架构，每个通道通过独立的传感器测量控制所需的发动机参数[4]。当1个通道的传感器发生故障时，可以切换到另一通道传感器的测量值进行控制，从而保证发动机正常工作[5-6]。然而，由此带来1个问题，即当其中1个通道传感器由于安装松动、工作环境恶劣等因素，发生软故障而偏离真实值，由于没有其它参考，很难判断究竟是哪个余度发生了故障。在20世纪70年代，Wallhagen等[7]就针对上述问题提出了利用解析余度模型来对传感器进行诊断，提高航空发动机控制系统的可靠性；从80年代开始，美国的科研机构围绕解析余度技术及其应用开展了系列研究，并在F100发动机上进行了试验验证[8-11]。

利用极端学习机（Extreme Learning Machine，ELM）算法建立航空发动机的传感器解析余度模型，对关键传感器的参数进行估计，可为FADEC系统传感器故障诊断提供解析余度，提高FADEC系统的可靠性[12-16]。虽然ELM算法的输入层权值和隐含层偏置可随机产生，然而，不适宜的随机值也会影响估计的精度和算法的稳定性。为此，本文利用改进的微分进化(Improved Differential Evolution,IDE)算法优化ELM的输入层权值和隐含层偏置，构建基于IDE-ELM的航空发动机传感器解析余度模型[17]。同时，采用K-均值聚类对用于试验数据进行处理聚类处理，剔除相似数据，提高训练的速度和精度[18-19]。

1 IDE-ELM算法

式中：wi=[wi1，wi2，…，win]T，为连接隐含层第 i节点与输入层节点的权值；bi为隐含层第i节点的偏差；βi=[βi1，…，βim]T，为连接隐含层第 i节点和输出层节点的权值。

式（1）的N个方程可以写为矩阵形式

其中

式中：H为神经网络的输出层矩阵，H的第i列是相对于输入x1，…，xN的第i个隐含层节点的输出向量。

输入权值wi和隐含层节点偏差bi是随机给定的，输出权值β由下式求得

式中：H†为网络输出层矩阵H的Moore-Penrose广义逆。

通过求解式（5）可得式（2）的最小二乘解

引入正则化因子C，则式（6）可改写为

式中：I为单位矩阵。

由于ELM的输入层权值wi和隐含层节点偏差是随机给定的，为获得更好的泛化能力，需要的隐含层节点数要明显多于BP、LM等传统算法，这就会相对占用更多的系统资源，增加系统的响应时间[14]。特别是当隐含层节点数很多时，隐含层矩阵H可能为病态矩阵，导致泛化能力差。为了减少隐含层节点数，提高ELM算法的稳定性和精度，本文利用IDE算法优化ELM的输入层的权值和隐含层偏置，形成IDE-ELM算法，如图1所示。

图1 IDE-ELM算法

2 基于IDE-ELM的传感器解析余度模型设计

以某型大涵道比涡扇发动机为研究对象，其截面划分如图2所示。设计基于IDE-ELM的传感器解析余度模型，为FADEC系统双通道传感器故障诊断提供解析余度[20]。为了提高解析余度模型动态时的精度，将被解析余度模型的输出前p步以及p-1的数据也作为模型输入，p由实际情况确定，模型的拓扑结构如图3所示[21]。本文根据航空发动机实际需求，针对风扇转速N1、压气机转速N2、高压压气机进口总温T25以及压气机出口静压Ps34个关键航空发动机参数建立基于数据的解析余度模型。

图2 某型大涵道比涡扇发动机截面

图3 基于IDE-ELM的传感器解析余度模型结构

虽然航空发动机动力学具有高度的非线性，但是在全包线范围内并不是所有工作点的数据都是独立的，很多数据之间存在非常大的相关性，没有必要将所用采集到的数据都用来训练IDE-ELM模型。此外，鉴于ELM算法是通过求广义逆来训练模型的特点，当存在大量训练样本相似时，会导致H矩阵的奇异，虽然通过正则化可以在一定程度上避免H矩阵的奇异，但会影响模型的训练精度。因此，本文借助模式识别中的K-均值聚类方法将数据根据Mahalanobis距离进行聚类[19]。K-均值聚类的结果就是产生k个类，每类有1个质心，然后计算当前状态与k个质心的Mahalanobis距离，将当前状态归属于离k个质心Mahalanobis距离最近的类中，最后分别从每类中随机选择1组数据组成k个样本训练模型[18]。

本文以航空发动机某次飞行试验数据作为训练样本，共采集试验数据59563组，各参数对油门杆角度PLA的响应如图4所示，图中数据均为归一化之后的数据，横坐标为按照100 ms间隔采样的飞行试验数据样本序列。为了选择与 N1、N2、T25、Ps3相关性较强的输入参数，采用相关分析法从发动机可测参数中选择模型的输入参数，见表1。

图4 飞行试验数据中各参数的变化曲线

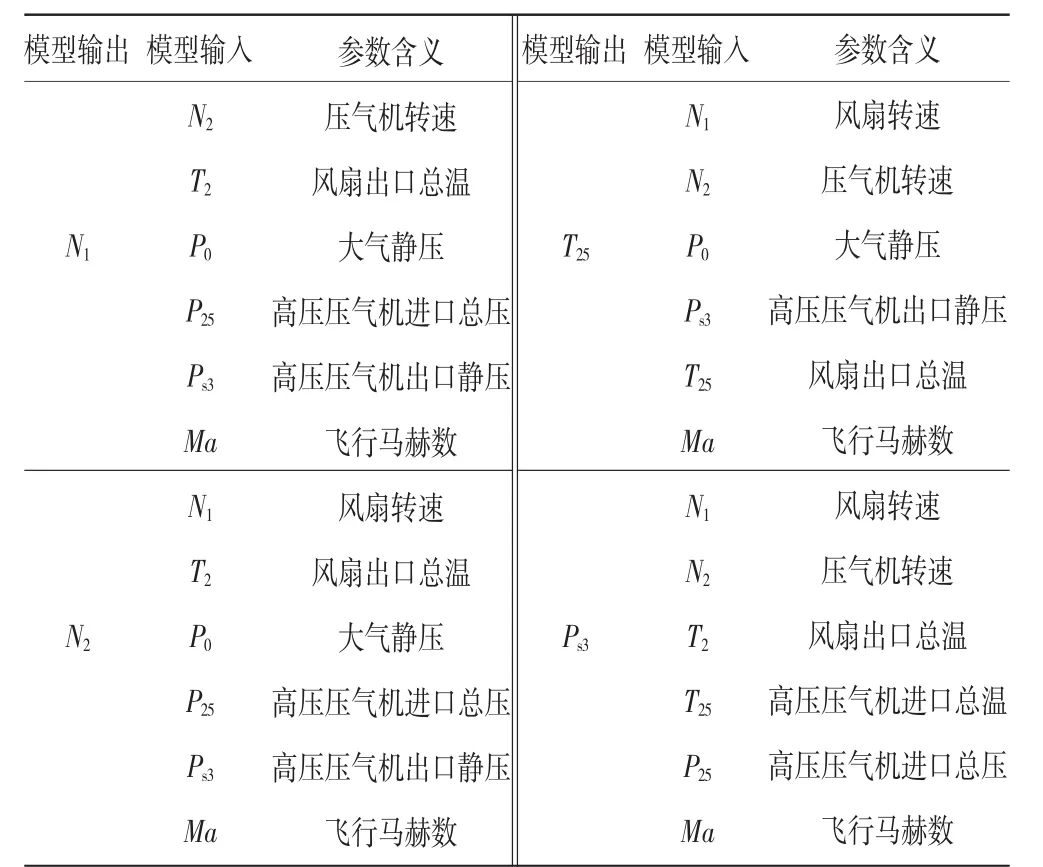
表1 各解析余度模型选择的输入参数

3 试验分析与验证

为了使模型的输入参数具有相同的权重，对所选的参数归一化到[0,1]。同时，选用相对误差(Relative Deviation)作为性能衡量指标。

通过 K- 均值聚类选取的 N1、N2、T25、Ps34 个解析余度模型的训练样本分别为1987组、1986组、1988组、1984组；在训练IDE-ELM的过程中，选取ELM 的隐含层节点N~分别为 30、32、28、35，正则化因子都为C=106；此外，由于进行FADEC系统的双通道传感器诊断时需要进行周期确认，本文选择p=6。N1、N2、T25、Ps34个解析余度模型的测试效果分别如图5～8所示。

图5 N1传感器解析余度模型测试效果

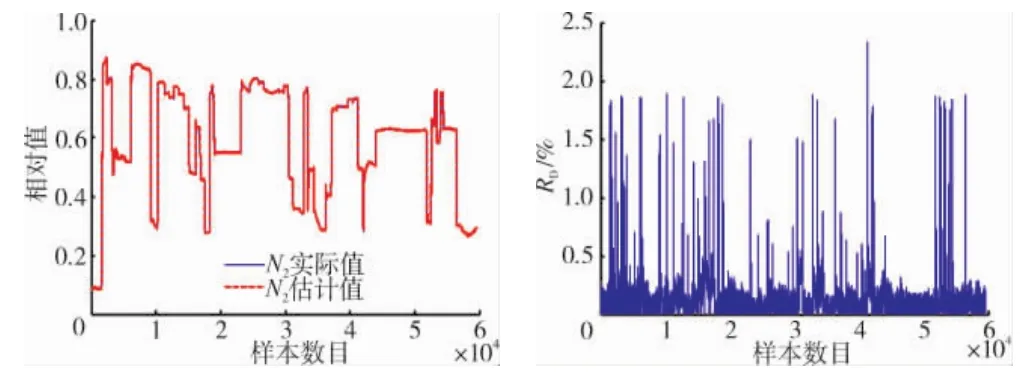
图6 N2传感器解析余度模型测试效果

图7 T25传感器解析余度模型测试效果

图8 Ps3传感器解析余度模型测试效果

从图中可见 N1、N2、T25、Ps3的估计值能够很好地跟踪飞行试验的实际值，相对误差基本都在2%以内，稳态的误差基本都在1%以内，能够满足传感器解析余度模型的精度要求。虽然通过K-均值聚类只选择了很少一部分数据用来训练模型，但是这些数据样本能够反映发动机各参数之间的特征。因此，本文基于K-均值聚类和IDE-ELM建立的传感器解析余度模型具有很好的精度，可为FADEC系统双通道传感器的故障诊断提供参考，提高传感器故障的检测率。

4 总结

本文提出了1种基于K-均值聚类和IDE-ELM算法建立航空发动机传感器解析余度模型的方法。基于K-均值聚类对试验数据进行聚类，然后针对聚类处理后的样本，采用IDE-ELM算法训练模型。该方法避免了飞行试验数据中冗余数据对训练效果的影响，采用IDE优化ELM的输入层的权值和隐含层偏置，可以减少隐含层神经元数目，降低网络的复杂度；基于K-均值聚类和IDE-ELM算法建立的模型，经过飞行试验数据验证表明该传感器解析余度模型具有较高的精度，可用于FADEC系统双通道传感器的故障诊断。