平面向量基本定理常用题型归纳

☉湖北省秭归县第一中学 梅 杰 何 尧

平面向量基本定理：如果e1，e2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a，有且仅有一对实数λ1，λ2使得a=λ1e1+λ2e2.

平面向量基本定理是正交分解和坐标表示的基础，它为“数”和“形”搭起了桥梁，在向量知识体系中处于核心地位.笔者对近十年高考有关平面向量基本定理题目作了系统研究，认为大致分为以下题型：

一、基本题型随处可见

1.直接利用λ1，λ2唯一性求解

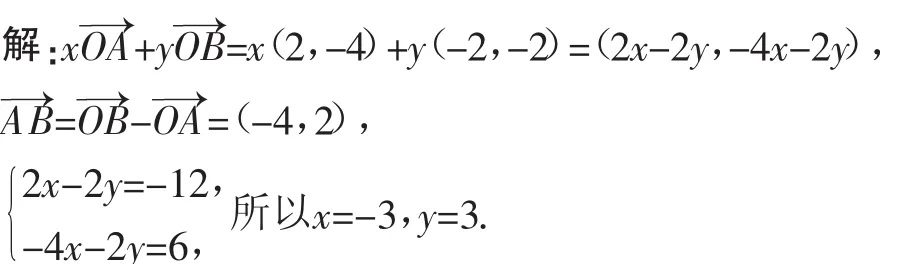
2.构建三角形，利用正余弦定理求解

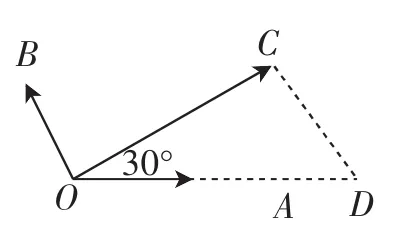
图1

解：过C作CD∥OB交OA的延长线于D，

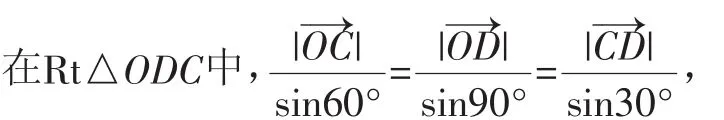
二、共线问题常考常新

1.感受平面内三点共线的结论在解题中简明快捷

常用结论：如图2，点O是直线l外一点，点A，B是直线l上任意两点，求证：直线上任意一点P，存在实数t，使得关于基底{OA，OB}的分析式为（1-t）·.

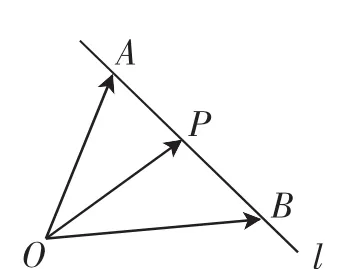
图2

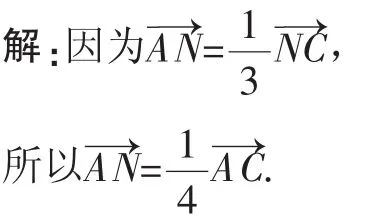
因为B，P，N三点共线，

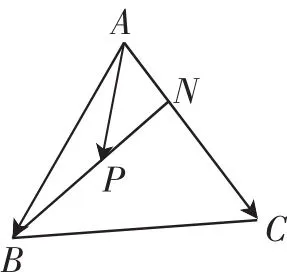
图3

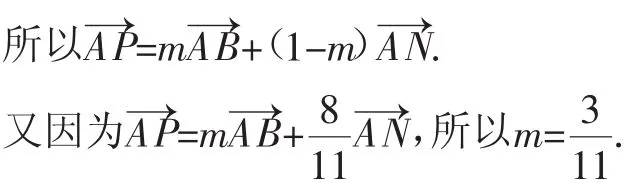
2.感受向量数形二重性在证明平面几何中独特魅力

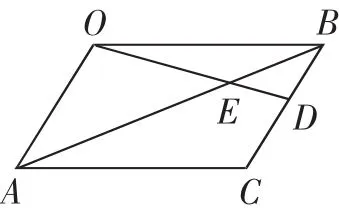
图4

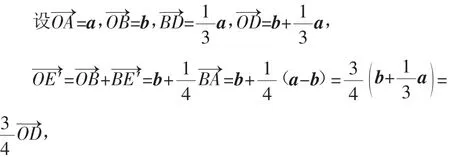
三、区域问题渐成热点

由平面内三点共线定理拓展可以研究区域问题，为解决线性规划问题画出可行域提供理论上的依据和操作上的便利，也可以解决向量中类似于点所在位置问题.

定理：设O，A，B为平面内不共线的三个定点，动点C满足O—→C=x（x，y∈R），记直线OA，OB，AB分别为lOA，lOB，lAB，平面被分成如图5的7个部分（Ⅰ—Ⅶ），得出结论表1，表2.

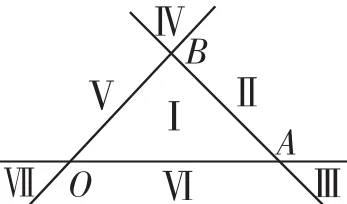
图5

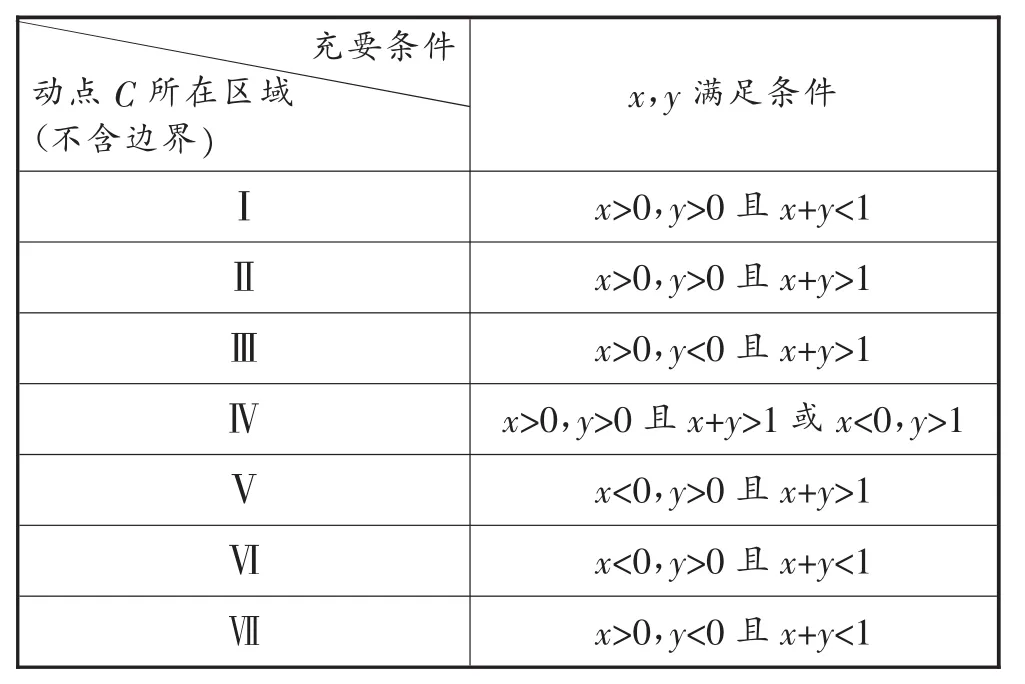
表1

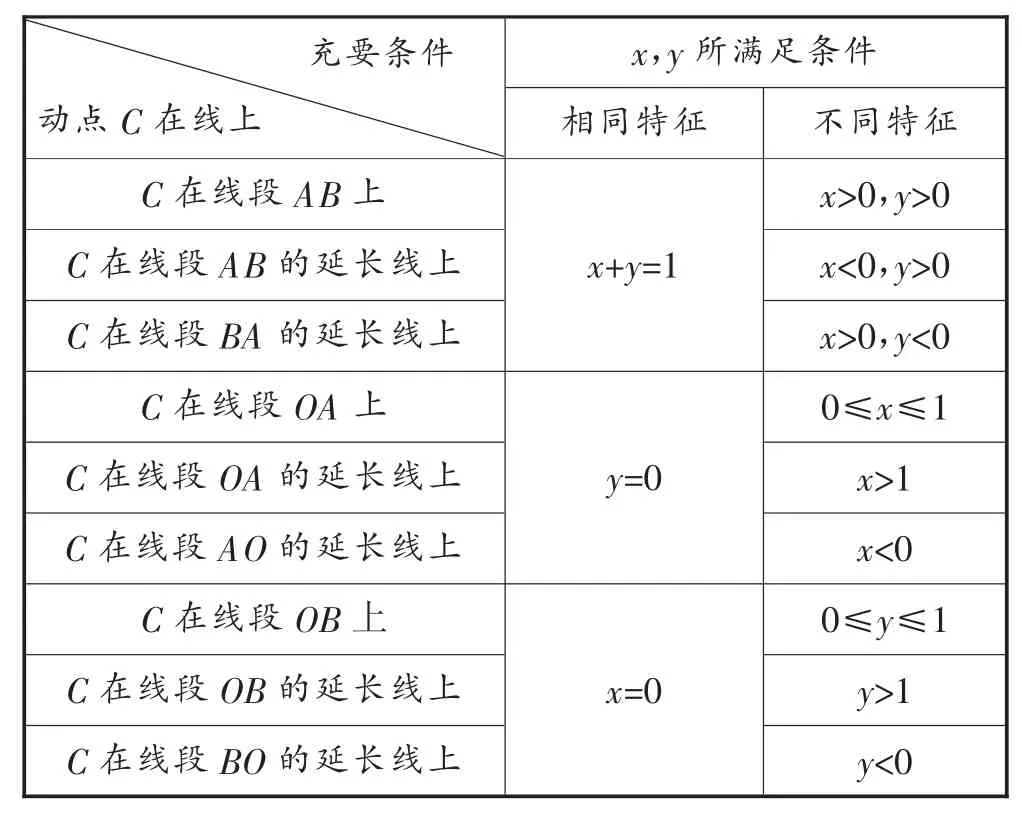
表2

在近十年高考题中，区域问题常以下面两种题型出现.

1.固定动点所在的位置，判断系数满足条件

例5 如图6，平面内的两条相交直线OP1和OP2将该平面分割成四个部分，Ⅰ，Ⅱ，Ⅲ，Ⅳ（不包括边界），若O—→P=a，且点P落在第Ⅲ部分，则实数a，b满足（ ）.

A.a＞0，b＞0 B.a＞0，b＜0 C.a＜0，b＞0 D.a＜0，b＜0

答案：B.

例6 如图7，OM∥AB，点P在射线OM，射线OB及AB的延长线围成的阴影部分内（不含边界）运动，且O—→P=，则x的取值范围是______，当x=-时，y的取值范围是______.

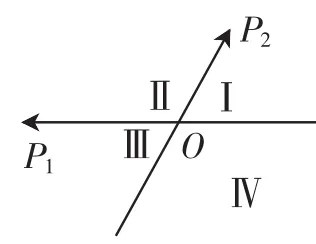
图6

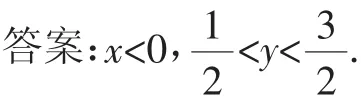
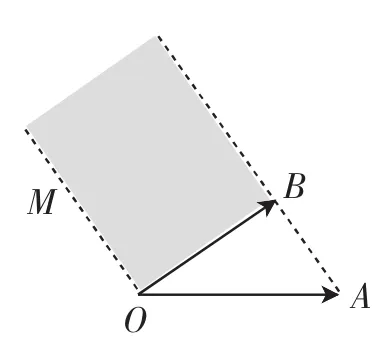
图7

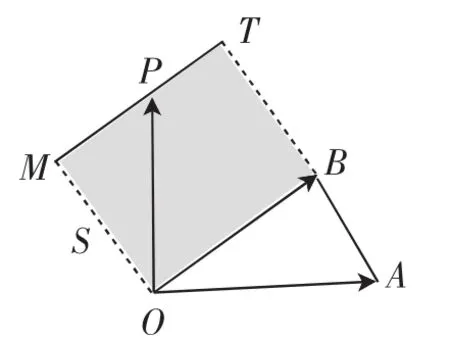
图8

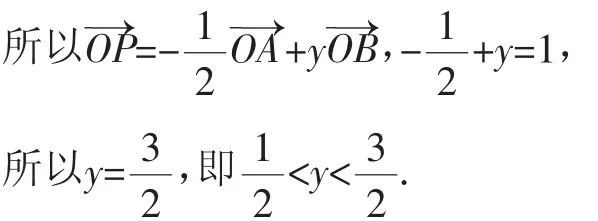
2.固定系数满足的条件，判断动点所在位置

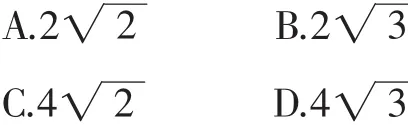
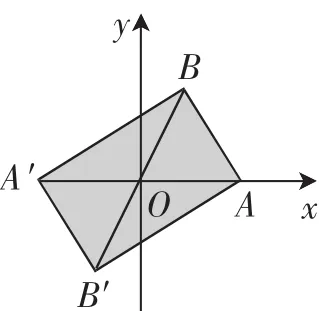
图9

答案：D.

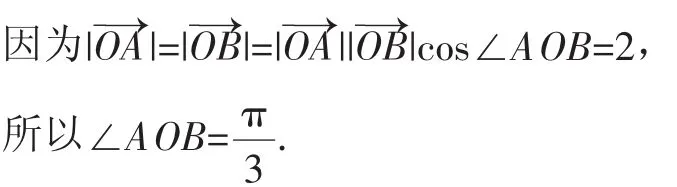
因为在第一象限，λ＞0，μ＞0，