分类讨论思想在高中数学解题教学中的渗透

2018-09-15江苏省苏州市吴江区平望中学吴建琴

中学数学杂志 2018年17期

☉江苏省苏州市吴江区平望中学吴建琴

高中数学解题中往往会遇到问题逐渐复杂并且无法采取统一方法求解的情况，对复杂情况进行多种情形的分析并分别根据一定标准进行解题即为我们通常所说的分类讨论的解题方法，根据多种可能将解决的问题由大化小、由整体化部分、由一般化特殊进行分类讨论是很多复杂问题的有效解决之道.不过，很多高中生在解题中运用分类讨论思想的意识与能力都需要教师在具体的教学中进行有意识的培养.

一、分类讨论思想的概述

准确攫取数学本质属性的相同点与不同点并将研究对象进行各种不同分类的研究即是我们数学教学中经常提及的分类讨论思想.分类与比较唇齿相依，不过，分类往往会因为衡量标准的不一致而获得更多不同的结果.教师在实际教学中应有意识地为学生多创造应用分类讨论思想的机会并帮助学生提升应用这一思想的能力，使学生能够在分类讨论思想的具体应用中做到有的放矢.

二、分类讨论思想的应用原则

分类讨论思想需要根据具体问题的条件或者性质进行清晰而准确的分类，不仅如此，解题时还应做到层次分明且不重不漏，越级讨论的现象在具体问题的解决中是不应该出现的.

例如，证明对于集合B成立的命题就可以把集合B分成若干个非空真子集Bi（i=1，2，3，…，n）（n≥2，n∈N），并使集合B的每个元素属于且仅属于其中的一个子集，即：（1）B1∪B2∪B3∪…∪Bn=B；（2）Bi∩Bj=Ø.

再如椭圆中的一个例子：

学生对于m＞0且m≠5以及m与5之间的大小对椭圆焦点产生的影响是比较容易理解的，因此，此题求解时可以根据m的取值范围来讨论，即分0＜m＜5与m＞5这两种情况.

三、分类讨论思想在解题中的应用

1.概率中的分类讨论思想

例1 设集合I={0，2，4，6，8}，选择I的两个非空子集A和B，如果使B中最小的数大于A中最大的数，则一共存在多少种不同的选择方法呢？

分析：根据已知条件，（1）A和B是I的两个非空子集，（2）B中最小的数大于A中最大的数，这两个条件又应该怎样实现呢？分类讨论是此时最为合理的方法.

①B中最小的数为2，此时A有1种选法，即A={0}，B有8种不同选法，即4、6、8这三个元素可以在B中也可以不在.

②B中最小的数为4，此时A有3种选法，即A为{0}，{2}，{0，2}，B有4种不同选法，即6、8这两个元素可以在B中也可不在.

③B中最小的数为6，此时A有7种选法，即A为{0，2，4}的非空子集，而B有2种选法，即8这一元素可以在B中也可不在.

④B中最小的数为8，此时A有15种选法，即A为{0，2，4，6}的非空子集，而B只有1种选法，即B={8}.

综上所述，共有1×8+3×4+7×2+15×1=49（种）选择方法.

2.不等式中的分类讨论思想

例2 设k∈N，求满足不等式|m|+|n|＜k的整数解组的（m，n）解集.

分析：若想直接给出此题的答案自然是比较困难的，因此，可以将k看成参数，与k相关的是整数解的组数，将其设为g（k），从特殊情况着手并探求其中的计算规律，作出猜想后证明其结论.

当k=1时，有解（0，0），即g（1）=1；

当k=2时，有解（0，0），（0，±1），（±1，0），即g（2）=1+4=5；

当k=3时，有解（0，0），（0，±1），（0，±2），（±1，0），（±1，±1），（±2，0），即g（3）=1+4+4×2；

当k=4时，有解（0，0），（0，±1），（0，±2），（0，±3），（±1，0），（±1，±1），（±2，0），（±3，0），（±1，±2），（±2，±1），

即g（4）=1+4+4×2+4×3.

猜想：g（k）=1+4×1+4×2+…+4（k-1）=1+2k（k-1）.

由此可得递推式：g（k）=g（k-1）+4（k-1）.

3.函数中的分类讨论思想

学生在具体的解题过程中往往因为分类讨论意识薄弱而无法清晰明确哪些问题需要分类讨论，有的学生即使能够明白哪些问题需要分类讨论，但在具体分类中却无法做到科学合理.因此，教师在实际教学中应结合教材内容启发、诱导学生对问题的本质进行思考，使得分类讨论思想的本质以及具体问题的本质清晰地展现出来，并因此使学生能够在解题中不断强化分类意识.比如，在函数概念、性质等研究中会用到分类讨论等等.

例3 对数函数y=logax中底数a不一样时会导致函数图像的不同，因此，教师在对数函数图像性质的具体教学中可以引导学生进行分类讨论以获得更加清晰的思维和理解.

（1）当a＞1时，函数定义域为（0，+∞），值域为R，函数非奇非偶，且其在定义域内单调递增.

（2）当0＜a＜1，函数定义域为（0，+∞），值域为R，函数非奇非偶，且其在定义域内单调递减.

教师根据底数a＞1和0＜a＜1这两种情况进行了分类讨论并得出了对数函数的不同性质，学生了解不同分类对整个函数性质影响的同时还能在具体解题中进行完整的分类解题.

例4 已知函数f（x）=cos2x+asinx-a2+2a+5有最大值2，则实数a的取值如何？

4.几何中的分类讨论思想

例5 如图1，在△ABC中，AB=AC，△ABC内有任意一点O，且∠AOB＞∠AOC.

求证：OB＜OC.

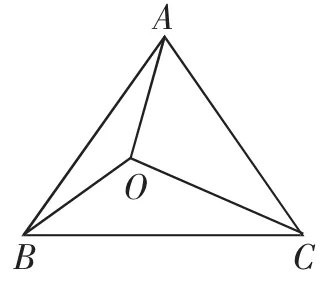
图1

证明：设∠AOB=α1，∠AOC=α2，∠ABO=β，∠ACO=γ，则由正弦定理得

又因为∠AOB＞∠AOC，即α1＞α2，且α1+α2＞180°，得90°＜α1＜180°，0°＜α2＜180°.

在此区间sinα2为非单调函数，因此，需要分类讨论：

①当α2≥90°时，因为α1＞90°，且α1＞α2，则sinα1＜sinα2，所以sinβ＜sinγ，且β、γ＜90°，则β＜γ.

②当α2＜90°时，因为α1＞90°，则180°-α1＜90°，又α1+α2＞180°，得α2＞180°-α1，则sinα1=sin（180°-α1）＜sinα2，所以sinβ＜sinγ，且β、γ＜90°，则β＜γ.

综上，∠ABC=∠ACB，∠OBC＞∠OCB，所以OB＜OC.

四、应用分类讨论思想时的注意点

1.明确分类讨论的原因

问题为什么需要分类、又应该根据什么来分类是学生解题时首先要弄清楚的，只有这样，学生才能准确定位分类的标准并做到不重复、不遗漏.数学学科中的某些概念、定义、定理、性质、法则、公式等都是分类给出并呈现一定系统性的，故而使得这些问题的解决需要运用分类讨论的思想.

2.掌握分类讨论的方法

学生在解决具体问题时应特别注意分类的统一标准并因此进行准确、合理的分类，只有这样才能在解题中做到不重不漏，因此，教师在分类讨论运用于解题的教学中应教会学生以下原则：（1）分类标准明确清晰；（2）分类讨论对象不能重复且遗漏；（3）当多个分类讨论的对象存在时应采取分层次的分类讨论，每个层次中又必须都有统一的分类标准.