从两道解析几何问题谈教学中“说”数学与“做”数学

2018-09-15江苏省无锡市堰桥高级中学陆旌霞

中学数学杂志 2018年17期

☉江苏省无锡市堰桥高级中学陆旌霞

说数学和做数学对师生来说都不陌生，说数学泛指对数学问题解决方向的思考和尝试，未必一定可做；做数学泛指对问题的具体尝试，能做也未必一定能讲清楚，使人接受.因此，对数学教学中的“说”与“做”，教师必须有清晰的认知，要从理论中有一定的思辨.

说数学做数学思维性思维广度广，可操作性未必能实现思维深度深，但思考角度较少操作性操作性不强，更多是一种猜测操作性强，是对知识的实战运用对比优点是思维广度、发散性思维得到了培养优点是亲身经历了对不同问题方法取舍的实战

因此可以这么说，说数学更多的是一种“探路”，而做数学是真正的“走路”.但在说的过程中不做，是不能理解是否真的可以解决问题；反过来一味地靠直觉思维做，而没有更深、更广的思、说数学，很难获得更好的思维层次，因此两者的相辅相成是教师教学更需要关注的.

一、先说再做

说，是思维过程的语言表述形态.而思维的活跃性，往往决定了能否找出合适的方向，因此思和说成为问题解决的首要探路方向.笔者就某一问题进行了学生探索的记录，跟读者一起来看看.

问题1：如图1，过x轴上一动点A（a，0）引抛物线y=x2+1的两条切线AP，AQ，P、Q为切点，设切线AP，AQ的斜率分别为k1和k2.

（1）求证：k1k2=-4.

（2）试问：直线PQ是否经过定点？若是，求出该定点坐标；若不是，请说明理由.

分析：本题是笔者给本备课组一次组内说题比赛时选用的一道圆锥曲线题.请教师从说数学的视角首先说一说解决的可能性，然后从做一做的视角尝试.主要是为了考查教师自身解决圆锥曲线问题的能力.

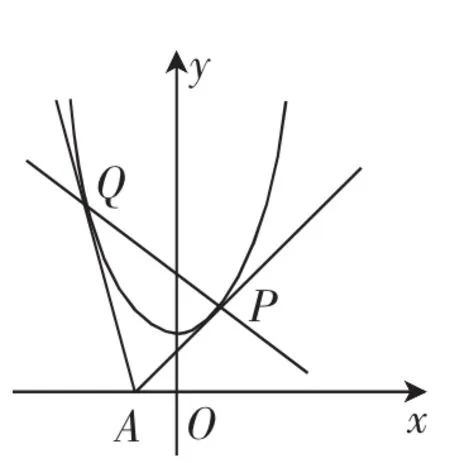
图1

教师甲（新教师）：我从最根本的角度思考，利用相切问题判别式等于0来求解，我觉得这是最简单的思维方式，对于第（2）问，要求定点只需要写出直线方程即可教师乙（5年教龄）：我是想到了算两次的想法，解析几何中算两次的使用非常多，本题中P、Q为切点，显然利用了同理算两次的原理，因此我是从这样的斜率角度去思考教师丙（1 0年教龄）：对于第（1）问，可以从方程思想出发思考，显然是过一个点引两条切线，其斜率是同一方程的两解，因此可以认为方程思想合适，第（2）问我倒是认为算两次使用比较合理

说的仅仅是思路，接下来请教师试一试，他所说的方式到底能不能行得通？

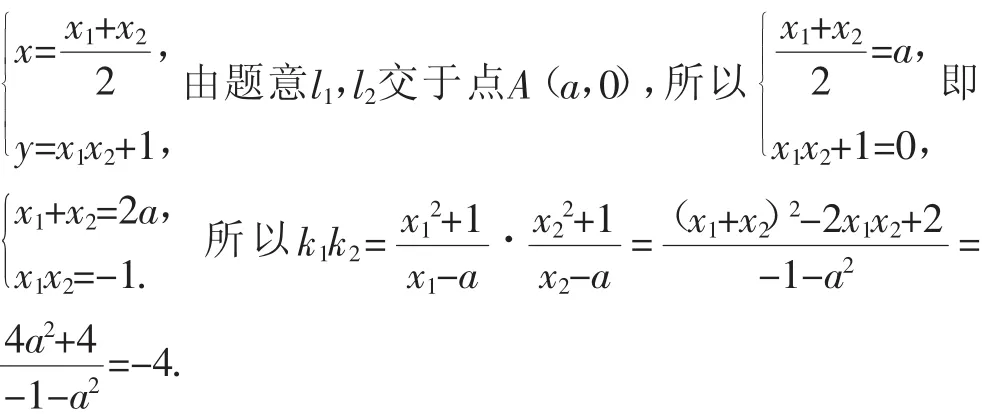
教师丙（10年教龄）法3：（1）设过A（a，0）与抛物线y=x2+1相切的直线的斜率是k，则该切线的方程为y=k（x-得x2-kx+（ka+1）=0，故Δ=k2-4（ka+1）=k2-4ak-4=0，则k1，k2都是方程k2-4ak-4=0的解，故k1k2=-4.

（2）设P（x1，y1），Q（x2，y2），故切线AP的方程是x1x+1，切线AQ的方程是.又A点在AP、AQ上，所以y1=2x1a+2，y2=2x2a+2，则直线PQ的方程是y=2ax+2，则直线PQ过定点（0，2）.

二、边做边说

刚刚谈到了先说后做，这样的方式存在一个很明显的问题，即万一说的思维并不能实现，怎么办？因此，现在说数学和做数学相比，并不是一先一后的方式，更多的是以并存的方式实现和进行的.研究一个课题教学问题2.

问题2：设A和B为圆周x2+y2=1上的两个动点，且满足与圆内一定点，求过点A和B的两条切线的交点M的轨迹方程.

分析：本题是笔者改编自江西高考理14题，切点弦的考查是热点问题，也是难点问题.请学生在不断尝试过程中，边做边说，实现问题的解决和思维的螺旋上升.考虑角度：圆方程是最为特殊的二元二次曲线，学生不难求得其切点处的切线方程；另一问，从∠ANB=可获得等量关系，进而得到A，B坐标的关系，最终解决切点弦方程.

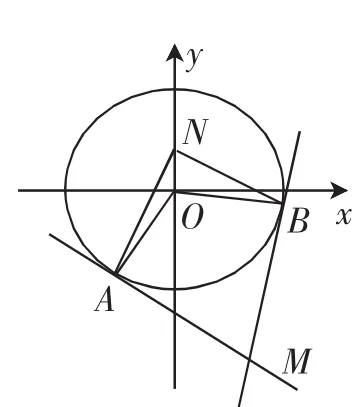
图2

师：思考本题，看看怎么解决？

师：请试一试.

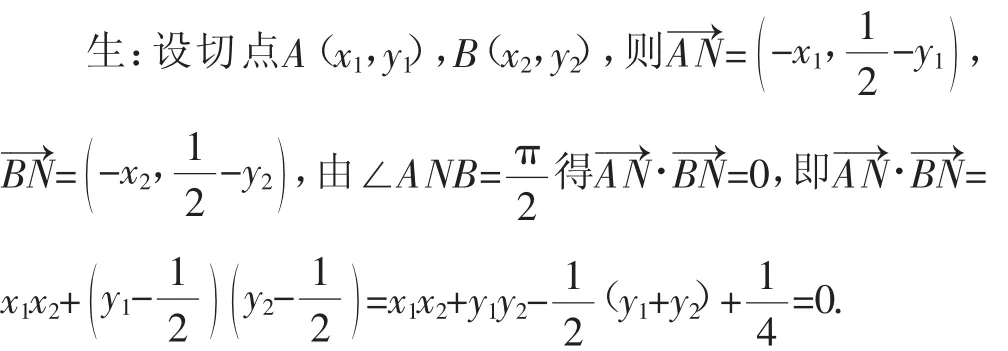
师：到此处，请你思考，你联想到了什么？

生：从这个结构来说，自然是韦达定理.

师：需要跟哪些点有关的韦达定理？

生：自然是直线AB方程有关的韦达定理.

师：那么现在首先解决直线AB方程，思考：过圆C：x2+y2=r2外一点M（x0，y0）作圆的两条切线MA、MB，求切点A、B所在直线方程？

生：这个我做好了，可以利用点的坐标进行解决.

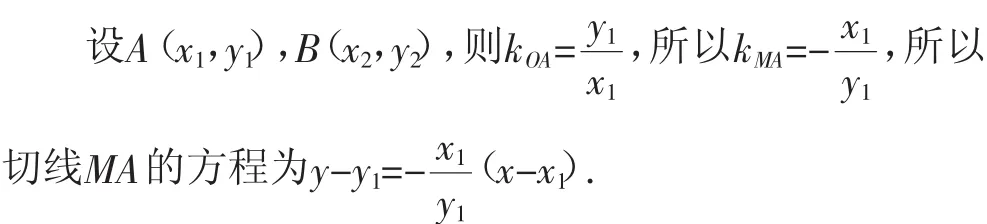
师：这位同学的思考是非常合理的，因为用“点”去解决解析几何问题是最为常规的方式.

生：我是这样解决的，我想利用我最熟悉的思路，即判别式等于0表示直线和圆相切，也能得到.设A（x1，y1），B（x2，y2），切线lMA：y=k（1x-x1）+y1，联立lMA与圆C方程得关于x的一元二次方程，由Δ=0得k=-x，得切线MA的方程

生：老师，我也可以用刚刚学的导数来求切线（.这位同学的做法很新鲜）设A（x1，y1），B（x2，y2），将y2=r2-x2两边对x求导得2yy′=-2x，于是有y′=-，所以切线MA的方程为y-y1=-（x-x1），即x1x+y1y=x12+y12=r2.同理lMB：x2x+y2y=r2.又M（x0，y0）在直线MA，MB上，则表示A（x1，y1），B（x2，y2）两点都在直线x0x+y0y=r2上，即切点弦lAB：x0x+y0y=r2.

师：非常好！这样我们可以对切点弦问题做一个总结了.