寻找最初的模样——几何意义的运用

☉江苏省苏州市苏苑高级中学 刘寒冰

众所周知，数学问题的解决往往具备多样性，既可以从代数视角出发，也可以从几何角度入手.从中学数学本身来说，我们不难发现这些知识往往是难点考查所在：函数、向量、几何、不等式，其中涉及图形的往往是几何视角，涉及变形的往往是代数视角，因此掌握合适的思考方向是第一准则.本文以函数最值为例，来探讨从“思考—选择—解决—反思”这一方法选择的过程，并从中理解某些函数在最值解决的过程中如何回到最初的“模样”.

问题1 |2x-1|+|x+2|＞a2+a 2+2对x∈R恒成立，求a的取值范围.

分析：本题是重庆高考真题，对于恒成立问题的求解，学生自然清楚主要求解函数y=|2x-1|+|x+2|的最小值.笔者请学生做了一次尝试，经过统计发现40位学生都是采用分类讨论求解函数最值，即：令y=|2x-1|+|x+2|=利用函数图像（此略）可得，当x=时，|2x-1|+|x+2|有最小值可以这么说，采用分类讨论解决本题无可厚非，但是思路的单一性使其在遇到更难的问题时势必陷入困惑.比如：

变式：求y=|x-1|+|2x-1|+|3x-1|+…+|10x-1|的最小值.

分析：此时我们不难发现学生陷入了沉思，其发现采用问题1分类讨论的方式花费时间较多，这一方法已经不是解决本题的主要方式，因此需要思考更合适的解决方法.

优化：让我们回到绝对值最值函数最初的模样来思考.初中对于绝对值这一概念的定义是什么样的？何为绝对值？|a-b|或|b-a|表示数轴上表示a的点与b的点的距离——这是绝对值几何意义的体现.不妨从最基本的几个绝对值函数最值思考，如：求y=|x-1|的最小值；求y=|x-1|+|x-2|的最小值；求y=|x-1|+|x-2|+|x-3|的最小值等等.显然，上述函数的最值从绝对值几何意义的视角考虑，既简单又清晰，无需分类讨论即能找到最值，此处不再赘述.那么对于多个绝对值函数的最值，可以从这一原理思考，进而利用几何意义获得优解.

原理：（1）偶数个零点：y=|x-a|+|x-b|的最小值（a≤b），当且仅当x∈［a，b］时取到；函数y=|x-a1|+|x-a2|+…+|x-an|（n为偶数且a1≤a2≤…≤an）的最小值，当且仅当

（2）奇数个零点：y=|x-a|+|x-b|+|x-c|的最小值（a≤b≤c），当且仅当x=b时取到；函数y=|x-a1|+|x-a2|+…+|xan（|n为奇数且a1≤a2≤…≤an）的最小值，当且仅当x=时取到.

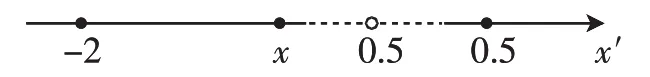
图1

图1

本质求解：利用绝对值几何意义，我们不妨再回首问题1.考虑到|2x-1|的几何意义不便直接表示，因此将其拆成两部分，利用绝对值的几何意义，即|x+2|，如图1，分析一维数轴中距离的含义可知：当

反思：我们发现，学生对此类问题的常用解决手段是分类讨论，但是借助分类讨论往往是费时费力，而且不易正确求解.学生偏爱分类讨论说明我们关于绝对值问题的解法教学是单一的，更多地关注了模式化的操作，而忽视了对概念本质的思考——绝对值最初的模样，即对绝对值几何意义的思考.

问题2 设x，y为实数，若4x2+y2=1，求2x+y的最大值.

分析：此题为二元最值问题，也是中学数学中重要的最值模型.学生对这样的模型主要是利用代数方式中的判别式法或者三角换元求解，也可以从几何意义的角度——直线的截距z=2x+y上思考，从而获得求解.这一问题的几何意义还是比较明显的，过程不再赘述.

变式1：设x，y为实数，若4x2+y2+xy=1，求2x+y的最大值.

变式3：若实数x，y满足x2+y2≤1，则|2x+y-2|+|6-x-3y|的最小值为______.

思考：变式1和问题2类似，但是其x和y具备了交叉混合项.此时直接的代数法三角换元显然失效，该如何思考？如果从几何意义的视角思考，方程4x2+y2+xy=1显然代表的是封闭曲线，而且显然不是圆的方程，那么对于学生来说，封闭的曲线只能从椭圆上去思考，因此利用换元可以将该曲线旋转回到标准形态，即令

1，表示焦点在y轴的椭圆里对曲线的思考体现了对知识理解的正确性，其截距的几何意义也是水到渠成.

将问题条件和结论换位思考，我们得到了变式2，对这一结论的代数化方向思考显然不太容易，问题的解决回到了最初的模样，即几何意义的思考.将 x2+y2+y看成两部分，第一部分几何意义显然是曲线上的点到原点的距离，第二部分是曲线上的点到x轴的距离，因此两段距离和的最小值是本题的几何本质.给出简析：（1）当y≥0时，设P（x，y），PP0⊥x，所以P（0x，0），|PO|=，所以原式=（|PO|+|PP0|）min，作O关于x+2y=2的对称点当Q，P，P三点共线垂直于x轴时，有最小值；（2）当y=0

0时，+y=2；（3）当y＜0时，+y=|PO|-|PP0|＞|P0O|-|P0P|＞|P0O|-|MP0|=2.综上所述，（

对于变式3，我们如何从几何意义的视角思考最值？显然二元变量x，y满足关系式x2+y2≤1，其几何意义非常的明显，即点（x，y）在以x2+y2=1为边界的圆及其内部，而可看成是点（x，y）到直线l1：2x+y-2=0，l2：x+3y-6=0的距离.因此从解析几何的角度我们可以得到如下的解法.如图2，直线l1、l2的斜率分别为-2、-，两直线间的夹角记为.令点P（x，y）是x2+y2≤1所表示区域上的一点，PN⊥l1，PM⊥l2，则F=|2x+y-2|+|6-x-，当P在l1与单位圆的交点处时有最小值3.

图2

反思：从几何意义的角度，让原本复杂的分类代数讨论变得简捷，因此对不少类型的函数最值，教师要引导学生从几何意义的视角去思考，特别是非解答题，这样的方式是有意义和高效的.

总之，数学问题的解决是双重性的，既要关注万能的代数方式（其解决方式较为全面、系统，但是稍显烦琐），也要注重具备直观感受的几何方式（快捷、方便，注重思维）.在函数最值领域，若能灵活地思考所求目标函数的几何意义，对于问题的解决显然是比较高效的.通过对几何意义的学习，我们回到了数学概念最真的本质，在茫茫题海训练中，我们回到了问题解决最初的模样——数学知识的几何意义，这不正是学习的重点和难点吗？