2018年以数学思想立意的高考试题评析

☉内江师范学院数学与信息科学学院 李雪莲 赵思林

数学思想方法具备很高的智力价值，是获得数学知识的重要手段，掌握了数学思想方法才能透彻理解数学知识，而且有助于创造能力的发展.数学思想是人们对数学内容的本质认识，是对数学知识和数学方法的进一步抽象和概括，属于对数学规律的理性认识.在高考考试大纲中，明确规定了对数学思想的考查.高中常用数学思想包括函数与方程思想、数形结合思想、转化与化归思想、分类与整合思想、特殊与一般思想、统计与概率思想、整体思想、极限思想、对称思想等.数学思想作为数学的精髓和灵魂，在高考数学中占有重要地位.比如，2018年不少优秀高考试题具有以数学思想立意的特点，对其中部分试题作了分析与点评.

一、函数思想

函数概念的发展经历了300多年，由函数概念所形成的函数思想是认识和处理变量关系的基本指导思想.函数思想是高中常用的一种数学思想，对提高分析变量关系能力具有重要的意义.

例1 （2018年全国卷Ⅲ理科12）设a=log0.20.3，b=log20.3，则（ ）.

A.a+b＜ab＜0 B.ab＜a+b＜0

C.a+b＜0＜ab D.ab＜0＜a+b

分析：需要比较a+b与ab之间的大小则需要构造出a+b与ab.若直接将a与b相加或相乘，要想得到结果是比较困难的.容易想到.由对数的运算性质可，再由对数与指数之间的关系可0.30.由指数函数的性质可得＜1.由对数函数的性质可以得到a＞0，b＜0，所以ab＜0.所以ab＜a+b＜0，选B.

点评：此题主要考查了对数与指数函数的性质.

二、数形结合思想

“数离形时少直观，形离数时难入微.”数与形是数学中研究的基本对象，在一定条件下两者可以实现互化.无论是“以数解形”还是“以形助数”都可以帮助学生将问题简化.教师要有意识的引导学生将数量关系与几何图形联系起来，激发解题思维.

例2 （2018年天津理数8）如图1，在平面四边形ABCD中，AB⊥BC，AD⊥CD，∠BAC=120°，AB=AD=1.若点E为边CD上的动点，则的最小值为（ ）.

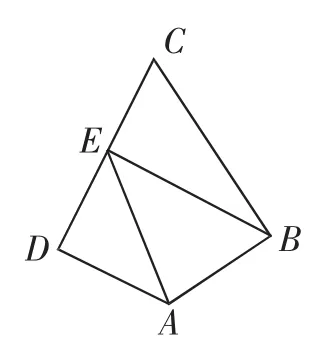
图1

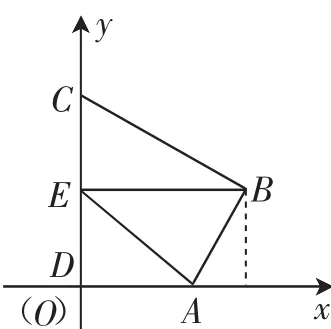
图2

点评：此题直接运用向量的知识不及运用解析法简单.

三、分类与整合思想

在解决某些问题时，被研究的问题包含了至少两种情况时，就需分类讨论.找到分类的标准，化整为零，在每个子类中单独解决后再将所有情况整合在一起.分类可以使研究对象化繁为简，更有利于解决问题.

例3 （2018年浙江卷10） 已知a1，a2，a3，a4成等比数列，且a1+a2+a3+a4=ln（a1+a2+a3）.若a1＞1，则（ ）.

A.a1＜a3，a2＜a4B.a1＞a3，a2＜a4

C.a1＜a3，a2＞a4D.a1＞a3，a2＞a4

分析：由a1+a2+a3=ln（a1+a2+a3+a4）可以联想到不等式lnx＜x-1（x＞0且x≠1）.故a4=a1q3＜-1，所以q＜0.当q＜-1时，a1+a2＜0，a3+a4＜0，即a1+a2+a3+a4＜0，与a1+a2+a3＞1矛盾.当-1＜q＜0时满足题意.所以a1＞a3，a2＜a4，选B.

点评：在解决此问题时关键是联想到不等式lnx＜x-1（x＞0且x≠1），此后还需对公比分类讨论.

四、化归与转化思想

化归与转化思想往往可以将一种问题转化为另一种问题，将复杂的、陌生的问题转化为简单的、熟悉的问题.

例4（2018年北京卷理科7）在平面直角坐标系中，记d为点P（cosθ，sinθ）到直线x-my-2=0的距离，当θ，m变化时，d的最大值为（ ）.

A.1 B.2 C.3 D.4

分析：由点P（cosθ，sinθ）的坐标可知，点P在单位圆上.直线x-my-2=0过定点（2，0）.问题转化为单位圆上的点到过定点（2，0）的直线的最大距离为多少.如图3所示，当直线为x=2，单位圆上的点（-1，0）到直线的距离最大为3.故选C.

点评：此问题通过转化后，便将求含有两个参数的式子的最大值的代数问题转化为求一个简单的、熟悉的几何问题.

图3

五、特殊化思想

对于一般情况成立，则对于特殊情况自然也成立.当遇到复杂的问题时，可以将其特殊化，简化问题，发现其规律或解题思路后再推广到一般情况.

例5（2018年全国卷Ⅰ理科10）图4来自古希腊数学家希波克拉底所研究的几何图形.图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC.△ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ.在整个图形中随机取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别记为p1，p2，p3，则（ ）.

A.p1=p2B.p1=p3C.p2=p3D.p1=p2+p3

分析：结论对于任意直角三角形都成立，则对于特殊的直角三角形自然也成立.可假设其三角形是直角边为2的等腰直角三角形.通过计算可得SⅠ=2，SⅢ=π-2，SⅡ=2.所以p1=p2＞p3.故选A.

点评：在解决选择题与填空题，这种不追求过程的题目时，往往可以将问题特殊化得到结果.对于需要展现问题解决过程的题目依然可以将问题特殊化，帮助探寻一般情况下的解题思路.

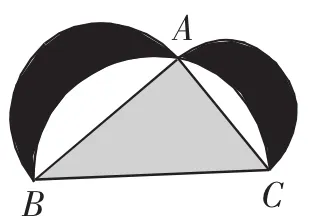
图4

六、概率与统计思想

概率与统计思想在生活中运用的十分广泛，基于数据的研究必然会运用到概率与统计思想，概率与统计思想涉及到数据分析与数学建模.

例6（2018年全国卷Ⅱ理科8）我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30=7+23.在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是（ ）.

分析：不超过30的素数有2，3，5，7，11，13，17，19，23，29共10个.随机选取两个不同的数共有=45（种）选法，其中和等于30的有{7，23}，{11，19}，{13，17}，共3种选法.所以其和等于30的概率为，故选C.

点评：此题包括了数据收集，数据整理，数据分析，还运用古典概型数学模型.

七、整体思想

学习数学必须树立整体思想，否则往往会得到矛盾的结论.从整体的角度考虑局部与整体的关系，可以使问题变得简单.

例7 （2018年全国卷Ⅲ文科11）△ABC的内角A，B，C的对边分别为a，b，c.若△ABC的面积为，则C=（ ）.

点评：此题将a2+b2-c2视为一个整体，结合余弦定理将可以很快捷地解决此问题.

除了上述思想外，高中常用数学思想还有建模思想、集合思想、隐含条件思想、逆反思想、参变数思想.在数学领域内要善于用数学思想的眼光去分析和解决问题，锻炼思维，激发创造性.