数学语言能力对高中生学习的重要性探究

☉辽宁省鞍山市第三中学 王 红

数学语言是一种独特的术语表达形式，它除了具备语言基本的功能以外，还具有较强的抽象性、严谨性和概括性，是数学信息传递的载体，在整个数学教学和解题中起着重要的作用.新课程标准中明确提出，中学生对于数学解题能力的掌握不仅仅要表现在对数学概念、公式、法则的理解上，还应体现在数学语言的转化和应用上.因此，学生的数学语言能力不仅是自身数学学习的重要组成部分，也是新课程标准对学生数学学习提出的基本要求.

一、数学语言能力概述

数学语言能力是学生在数学学习过程中，能够准确理解数学问题中所包涵的数学知识和思维及其所表达的数学思想，同时，还能够将数学语言作进一步的构造和转化，转化成为自己熟悉的语言，最终完成解题.总体上来说，学生的数学语言能力主要包括数学语言的理解能力、数学语言的转化能力、数学语言的操作能力和数学语言的表达能力等.较高的数学解题能力是数学解题的重要保障，能够准确理解题意，寻找其中的隐含条件，制定准确的解题计划，进而完成正确的解题过程.

二、数学语言能力的重要性

（一）理解和记忆数学语言是数学学习的基础

数学语言的一大功能就是用来描述数学问题，通过数学语言，来了解问题中所包含的数学信息，为解决数学问题打下基础.数学语言的抽象性和概括性，造就了在数学语言中会包含很多的数学隐含条件，如果学生数学语言能力不够，就会非常容易忽视这些隐含条件，最终导致解题出现错误.例如，看似简单的tanx，它里边蕴含了大量的数学信息：这是一个正切函数，它的周期是π，并且它还是一个奇函数，它的值域是（-∞，+∞），并且它在其定义域上是增函数，它的图像还是一个中心对称图形.因此，在数学学习和解题过程中，学生要关注数学语言中隐含的数学信息，这样才能够拓宽解题思维，提高数学学习和解题的能力.

解析：解决这一问题的关键在于数学语言的转化，将原题转化为点（，1）到直线y=2的距离.根据点到直线的距离公式来完成求解.很多学生之所以出错，就是因为忽略了题目中隐含条件.还有些学生不能够对数学语言做准确把握，将x=pcosθ，y=psinθ，正余弦顺序颠倒，导致出现错误.

（二）转换数学语言是拓宽数学思路的必要保障

学生对于数学语言的转换能力主要体现在数学问题、结构、易元、等价等问题的转换上，是学生解决数学问题的保障，尤其是在利用化归、数形结合等数学思想解决问题的时候，转换和改造数学语言的能力就显得非常重要.借助数学语言的转换能够激发学生的灵感，拓宽学生解题的思维，使学生明确解题的思路，寻找解题的方法.

例2图1是函数y=f（x）的图像，在区间［a，b］上存在n个不同的数x1，x2，x3，…，xn使得f，那么n的取值范围是多少？

图1

解析：这个问题从语言结构上来看，是由三种语言构成的，学生拿到手里难免会出现无从下手的状况，在解题的过程中，就需要对题目中的几何语言进行转换和改造，将题目中的几何语言转化为图形语言：在函数y=f（x）的图像上，有n个点与坐标原点连线的斜率相同，那么n的取值范围就是过原点的直线与函数图像交点的个数，根据图像就可以得出n的取值.这个问题很好地反映了很多问题的解决过程都是在数学语言的转化中实现的，尤其是在线性规划、立体几何、函数最值等部分问题的解题中，跟需要数学语言的转换来开拓学生思维，完成解题.

例3 对于不等式0≤x2+px+5≤1只有一个解，那么p的取值应该是多少？

解析：对于这一问题，学生如果单单是抓住数学符号语言这一项，就会觉得无从下手，思维就会受到限制，如果利用数学语言的转换能力，将这一符号语言转换为图形就可以方便我们寻找问题的突破口.将它转换为图形语言：抛物线y=x2+px+5与0≤y≤1直线之间的位置关系，这样，原来看似无解的数学问题便迎刃而解.

（三）构造数学语言能够帮助学生获得解题灵感

学生的数学语言构造能力主要体现在抽取问题的本质，将有用的数学信息进行构造，创造新的数学语言和数学模型的过程，在这个过程中，学生可以通过添加辅助线、限制数学条件等方式，获取解题灵感，最终来解决数学问题.

例4函数f（x）=（x-a）（x-b）+（x-b）（x-c）+（x-a）（xc），其中a＜b＜c，那么函数f（x）的两个零点分别位于的区间是（ ）.

A.（a，b）和（b，c）内B.（-∞，a）和（a，b）内

C.（b，c）和（c，+∞）内D.（-∞，a）和（c，+∞）内

解析：拿到这一题目很多学生会觉得无从下手，因为该题目中的函数表达式是含参的，我们就可以将这一问题转化为求方程根的问题，结合题目中给出的条件来构造函数y1=（x-a）（x-b）+（x-b）（x-c）=（x-b）（2x-a-c）和y2=-（x-a）（x-c），然后根据条件画出大致的函数图像，如图2，最后根据函数图像就可以推断出函数的两个零点的位置.

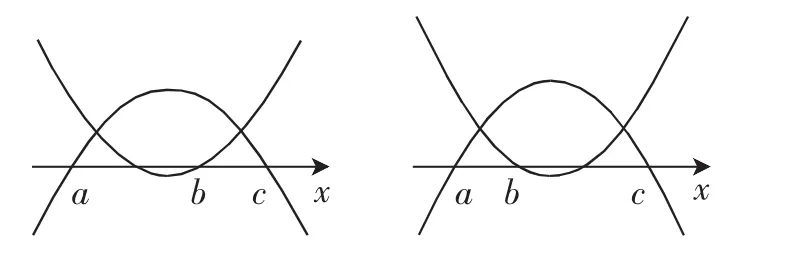
图2

例5 在空间坐标系O-xyz中存在一四面体，它的顶点坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），以z-O-x所在平面为投影面对四面体进行投影，得到的四面体的投影是（ ）.

解析：在这一问题中，题目中并没有给出既定的直观示意图，我们首先要将文中的符号语言转变成为图像语言，建立空间之间坐标系，然后再观察通过某一平面的正视图.作出图形以后，通过观察我们会发现，这个四面体构成的总的轮廓是一个边长为1的正方体，进而我们就可以围绕结论进行判断，选出正确的选项.

图3

（四）数学语言的操作能力是解决数学问题的关键

学生对数学语言的操作能力主要体现在对数学符号的理解、推理、运算等方面，尤其是在函数计算、不等式问题、数列等部分，对数学符号的运算推理非常多，如果学生在数学语言操作方面的能力偏弱，就会导致数学学习困难，数学问题难以解决.

解析：这一问题并没有涉及太多的数学语言，是一道直来直去的问题，主要就是考查学生对数列公式正确的操作能力.首先根据前n项和S=a+求出a的值，nn1再根据an=Sn-Sn-1求出an=-2an-1，最终得出列{an}是一个以1为首项，以-2为公比的等比数列.

三、小结

随着新课程改革的实施，高考数学在对学生考查的侧重点上出现了变动，逐渐加大了对学生数学语言能力的考查，尤其是在语义理解、转换等方面.灵活使用数学语言是数学学习和解决高考数学问题的重要前提，通过数学语言之间的灵活转换，能够开拓学生的思维，厘清题目隐含条件，帮助学生寻找解题突破口，最终取得解题的成功.H