经济增长、交通基础设施与换算周转量的动态关系研究
2018-09-14罗会华
罗会华
(湖南商学院 经济与贸易学院,湖南 长沙 410205)
一、引 言
改革开放后,特别是20世纪90年代以后实施财政分权政策和积极的财政政策,我国对交通基础设施进行了大量投资,如2008 年应对金融危机而推出的 4 万亿元经济刺激计划中,将近一半经费投向了铁路、公路等交通基础设施,交通运输得到了高速发展。铁路营业里程从1980年的5.33万千米增加到2016年的12.4万千米,公路里程从1980年88.83万千米增加到469.63万千米。旅客周转量从1980年的2281.3亿人/千米增长到2016年31258.46亿人/千米,货物周转量从1980年的11629亿吨/千米增长到186629.48亿吨/千米。人均名义GDP从1980的468元提高到2016年的53935元。
理论上,经济增长及交通基础设施改善可促进交通运输需求,从而提高客货周转量;交通基础设施建设会促进经济增长,客货周转量提高意味着区域市场一体化逐步实现,推动资源在区域间有效配置,也对经济增长起到了作用;经济增长导致对交通运输需求增加,或者外生冲击导致客货周转量提高,也会推动交通基础设施建设。但交通运输与国民经济发展之间具有复杂的关系,现实情况未必与理论一致,在不同的情形下,它们之间的关系可能有不同的表现。如Deng et al.(2014)发现运输基础设施存量与长期增长率之间存在非单调的关系,交通运输规模的经济增长效应显著地取决于现有运输网络的水平[1]。因此,现有的研究主要从实证的角度来探讨三者间的现实关系,特别是交通运输与经济增长的关系的实证研究一向是国内外学者关注的焦点。
许多文献采用允许内生变量存在的VAR模型(含向量修正误差模型,VECM)来检验交通运输与经济增长之间的动态关系。如Rafael et al. (1998) 、Kamps(2005)、Khadaroo (2008)、Eruygur(2009)、Pradhan & Bagchi(2013)、Cheteni(2013)、Mohmand et al.(2016)等采用了VAR或VECM来研究了交通基础设施与经济增长的关系,大多研究表明交通基础设施对经济增长具有正向作用[2~8]。国内研究方面,刘建强和何景华(2002)指出我国客货运量与GDP之间存在协整关系,货运量是GDP的格兰杰原因,但GDP不是货运量的格兰杰原因[9]。然而,林航飞和罗宇龙(2008)的研究表明公路货运量不是GDP的格兰杰原因,而GDP是公路货运量的格兰杰原因[10]。崔淑丹等(2008)检验了中国经济增长和货运周转量之间的互动关系,指出货运周转量的冲击对经济增长具有带动作用和持续效应,但经济增长对货运周转量没有显著影响[11]。王任飞和王进杰(2007)指出在基础设施与经济增长的互动关系中,基础设施促进经济增长居于主导地位[12];李芬和冯凤玲(2014)也指出经济增长对交通运输的引致需求作用不如交通运输对经济增长推动作用明显[13]。吕稼欢和范文强(2016)的研究也GDP带动交通运输的发展,交通运输对GDP的贡献率较小[14]。刘秉镰和赵金涛(2005)检验了交通运输网络密度与区域经济经济增长之间的Granger因果关系,指出交通运输网络密度与经济增长的关系存在区域异质性[15]。李煌伟、倪鹏飞(2013)通过实证研究发现,交通运输网络的改善加速了要素集聚,从而促进经济增长[16]。Deng et al.(2014) 的研究表明,当公路网密度低于0.17千米/千米2时,公路基础设施存量与经济增长之间没有显著的正相关关系,但当公路密度高于0.17千米/千米2时,公路密度增长对经济增长有显著的积极影响[17]。
已有研究的结论由于采用的样本差异,导致不少观点相异,但结论可归纳为三种:第一种认为交通运输对经济增长具有单向因果关系;第二种认为经济增长对交通运输具有单向因果关系;第三种认为交通运输与经济增长之间互为因果关系。针对交通基础设施与经济增长或客货量与经济增长的关系均展开了较多研究,但鲜有系统实证研究交通基础设施、周转量和经济增长三者间的动态关系。鉴于此,本文采用VECM来展开研究,利用1980—2016年我国实际人均GDP、交通网络里程与换算周转量时间序列数据来分析三者间动态关系。在VECM估计结果的基础上,通过脉冲响应来分析各变量对随机冲击的响应情况,通过方差分解来分析各变量的结构冲击对某个变量总变化的相对贡献度。
二、数据、变量与模型
(一)数据来源与变量
本文采用 1980—2016年中国时间序列数据进行分析,初始变量的数据来源于国家统计局网站。初始变量包括历年的名义人均GDP、国民生产总值指数(上一年=100)、货物周转量、铁路营业里程、公里营业里程、内河通航里程、铁路旅客周转量、公路旅客周转量、水运旅客周转量等。利用初始变量计算出历年的实际人均GDP、换算周转量和交通网络里程。
本文采用实际人均GDP来衡量经济增长。以1979年为基期,通过国民生产总值指数对名义人均GDP平减处理,得到实际人均GDP,用rcp表示实际人均GDP。
采用交通网络里程来反应交通基础设施存量。本文视铁路、公路及内河通航在运输上作用一致①,因此赋予相同的权重。因此,每年的交通网络里程就是把每年的铁路营业里程、公路营业里程、内河通航里程进行加总,即:交通网络里程=铁路营业里程+公路营业里程+内河通航里程,用mil来表示交通网络里程。
周转量分为旅客周转量和货物周转量,两者的单位不一致,旅客周转量的单位是每亿人/千米,货物周转量的单位为亿吨公里。如果两个都作为VAR模型的内生变量,将导致自由度损失过大。为此,本文采用换算周转量(Converted Turnover)的概念来综合,换算周转量是指将旅客周转量按一定比例换算为货物周转量,然后与货物周转量相加成为一个包括客货运输的周转量综合指标。具体计算方法是将旅客周转量区分不同运输工具按相应的换算比例,换算成货物周转量的计量单位进行加总求得。采用的换算比例如下:公路运输的换算比例:1吨/千米=10人/千米;内河水运的换算比例:1吨/千米=3人/千米;铁路运输的换算比例:1吨/千米=1人/千米。②因此,本文通过下列公式得到历年的换算周转量:换算周转量=货物周转量+(铁路旅客周转量/1)+(公路旅客周转量/10)+(水运旅客周转量/3),用ct来表示。
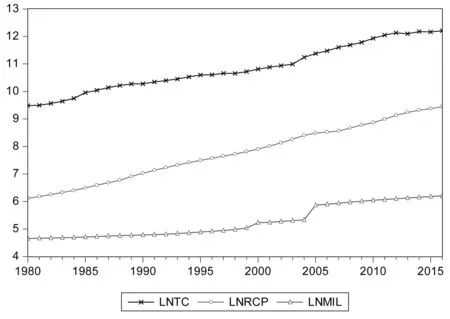
图1 各变量的对数值的时间序列图
本文对ct、mil、rcp进行对数化处理,lnct、lnmil、lnrcp的时间序列图如图1所示。可以看到,lnct、lnmil、lnrcp虽然不具有平稳的特性但具有相同趋势,直观判断可能存在协整关系。
(二)单位根检验
本文主要采用 ADF、PPERRON和DF-GLS三种检验方法来进行单位根检验,如表1所示。三种方法均显示lnct、lnmil、lnrcp三个序列为非平稳序列,但它们的一阶差分序列均为平稳序列,即lnctt~I(1),lnmiltI(1),lnrcpt~I(1),因此三者间可能存在协整关系,具备构建协整模型的前提条件。

表1 单位根检验结果
注:①检验统一采用含截距的方式;②括号中的数字为统计量的P值;③DF-GLS的检验为滞后1阶的统计值。
(三)向量误差修正模型
本文采用以VAR模型为基础的协整检验方法来分析变量间的短期和长期关系。内生变量为lnct、lnmil、lnrcp,构建的滞后p阶VAR模型如下:
yt=A1yt-1+A2yt-2+…+Apyt-p+εt,t=1,2,…,T
(1)
其中,yt=(lnctt,lnrcpt,lnmilt)′为(3×1)维随机时间序列向量,yt-p为内生变量yt的滞后p期的向量,A1,…,Ap均为(3×3)维待估参数向量;εt为(3×1)维经典随机扰动项向量,在VAR模型中一般称为新息(Innovation)。将式(1)进行协整变换,得:
(2)
(3)

(4)
式(4)即为向量误差修正模型(VECM),每一方程均为一个误差修正模型(ECM)。VECM中的调整参数向量,反映的是变量之间的均衡关系偏离长期均衡状态时,将其调整到均衡状态的调整速度。所有作为解释变量的差分项Δyt-i(i=1,2,3,…,p-1)的系数向量Γi(i=1,2,…,p-1),反映的是各变量的短期波动Δyt-i对作为被解释变量yt的短期变化Δyt的影响。
三、实证结果与分析
(一)VAR模型滞后阶数检验
一个关键问题是确定VAR模型中的最优滞后阶数p,如果p值过大,导致自由度减小,影响到VAR模型参数估计值的有效性;但如果p值过小,会导致随机扰动项自相关,导致参数的非一致性。为了确定出最优滞后阶数,本文采用FPE、AIC、HQIC、SBIC来进行选择最优滞后阶数,其准则是最小值即为优先模型,检验结果如表2所示。FPE、SBIC检验结果显示最优滞后阶数为2阶,但AIC 和HQIC选择3阶。因此,2阶和3阶都可作为最优滞后阶数,本文结合下面的协整检验来确定最优滞后阶数。

表2 VAR模型最优滞后阶数检验结果
(二)协整检验
鉴于lnct、lnmil、lnrcp为非平稳序列,因此需要进行协整检验,在变量协整的基础上建立VAR 模型。本文采用Johansen协整检验法对序列进行协整检验,通过特征根迹检验法(Trace检验)和最大特征值检验法(Max-Eigen检验)来进行检验;并根据VAR最优滞后阶数可能是2阶或3阶,选择起止滞后阶数时,采用(1,1)和(1,2)两种形式来进行检验,检验结果见表3。

表3 Johansen协整检验结果
检验结果显示:在选择起止滞后阶数(1,1)时,在 5%的显著水平下,特征根迹检验法表明序列之间至少存在2个协整关系,但最大特征值检验法显示序列之间不存在协整关系;在选择起止滞后阶数(1,2)时,在 5%的显著水平下,两种检验方法表明序列间存在着1个协整关系。因此,综合最优VAR滞后阶数检验结果和Johansen协整检验的结果,本文选择VAR最优滞后阶数为3阶。在滞后3阶的VAR模型中,存在1个协整关系,表明交通网络里程、换算周转量与经济增长之间存在长期的均衡关系。Johansen协整检验中,得到基于Johansen标准化约束下的协整方程为:
(5)
P值 (0.0452) (0.0971)
从长期均衡方程可以看到,换算周转量显著受到了实际人均GDP和交通网络里程的影响。实际人均GDP每提高1%,换算周转量平均提高0.521%;交通网络密度每提高1%,换算周转量平均提高0.512%。
(三)VECM估计结果及分析
尽管换算周转量与实际人均GDP、交通网络里程间存在着协整关系,然而实际经济生活中存在着各种扰动,导致变量短期内会偏离其长期均衡路径。根据Granger定理,当变量间存在协整关系,必存在误差修正机制。因此,本文估计出 VEC模型来分析短期波动时各变量间的关系。滞后2阶VECM的估计结果如表4所示。表中,ecm代表修正误差项且ecmt=lnctt-0.5213lnrcpt-0.5119lnmilt-4.117。根据VECM的估计结果,选择在10%显著性水平下的显著项,分析变量间的短期关系。
换算周转量短期变化(增长率)受到下列因素的显著影响:①受到滞后1期的自身增长率的正向影响,表明换算周转量变化具有一定的滞后作用。②受到滞后1期人均GDP增长率波动的正向影响,表明随着收入提高时,会增加对交通运输的需求,但对交通服务的消费具有滞后效应。③受到滞后1~2期的交通网络里程增长率的正向影响,表明当交通网络里程得到扩张时,会产生较大的劳动要素转移和商品转移的需求,导致换算周转量增长率提高,意味我国交通运输需求总体上仍然受到交通基础设施存量的制约。④当换算周转量偏离了长期均衡状态时,系统将以0.426的调整速度反向调整到均衡状态。

表4 VECM估计结果
注:①括号中值为T统计量的P值②“***”、“**”、“*”分别表示在 1% 、5% 和 10% 的水平下显著
实际人均GDP短期变化(增长率)受到下列因素的显著影响:①受到滞后1~2期的换算周转量增长率影响较大,表明交通运输增长对经济增长的作用明显,交通运输发展降低了贸易成本,提高要素和产品的流动性,促进了资源的优化配置,进而对经济增长起到长期影响。②受到自身滞后1期的增长率的正向影响,表明人均GDP增长具有一定的惯性,前期促进经济增长的因素在后期依然起到作用,如人力资本的提高。③受到滞后1~2期的交通网络里程增长率负向影响,两者负相关很有可能是因为我国交通基础设施大规模投资时,往往是经济处于衰退时,但经济增长具有惯性,导致交通网络里程增速增大时,人均GDP增速却是降低的。④当人均GDP偏离了长期均衡状态时,系统将以0.047的速度将人均GDP波动反向调整到长期均衡状态。
交通网络里程短期波动(增长率)受到滞后2期换算周转量增长率的正向影响,当滞后2期周转量发生较大波动时,可能导致交通基础设施供给不足,因此,会加大交通基础设施投资,而交通网络营业里程增加需要一定的建设时间。没有受到人均GDP增长率和自身增长率的显著影响,在一定程度上说明我国的交通基础设施建设体现为外生,并非由经济发展水平和基础设施存量来推动的,主要由中央的建设规划和地方政府的“晋升锦标赛”来推动。交通网络里程偏离了长期均衡状态时,系统以0.006的速度反向调整回长期均衡状态。
(四)脉冲响应分析
VAR模型只有在自身稳定后才能进行脉冲响应分析、方差分解,否则将影响响应冲击函数的标准差。判断VAR模型是否稳定,主要根据VAR模型的特征方程的根是否在单位圆内,即特征根的模小于1。通过表5可以发现,该VAR(3)模型是稳定的。因此,可以开展脉冲响应分析和方差分解。

表5 模型稳定检验
脉冲响应用来刻画随机扰动项一个标准差的冲击对每个内生变量未来取值的影响,直观地衡量变量之间的动态交互作用和影响效应。分别给换算周转量、实际人均GDP和交通网络里程一个标准差大小的冲击,得到各变量未来30期的脉冲响应曲线图,如图2所示。

图2脉冲响应曲线
来自换算周转量的一个标准差大小的随机冲击,对自身的冲击在第1期为最大,导致换算周转量增长率为6%,但随着时间推移快速衰减,在第15期后,收敛于0.99%,表明换算周转量对自身的冲击程度较小且不具有长期效应,如2003年“非典”导致换算周转量增长率降低到5.1%,但经过2005的反弹后恢复到均衡水平;对人均GDP有正向影响,第1期的冲击作用导致人均GDP增长率为0.54%,随着时间推移递增,在第15期后,收敛为1.2%,说明换算周转量促进要素和商品流动,导致资源合理配置,将对经济增长具有长期效应;对交通网络里程的影响在第1期达到了最大,导致交通网络里程增长率为2.9%,第2期后快速减弱,并在第15期收敛为0.69%,说明当我国的交通运输需求超出现有的交通基础设施的承载力时,交通网络里程将在第1期和第2期内的增长幅度最大,这符合交通基础设施的建设规律,一般需要几年建设期才能投入使用。
来自人均GDP的一个标准差大小的随机扰动,对换算周转量的冲击在第1期为0,随后递增,第15期后,换算周转量增长率收敛于1.62%,表明人均GDP对换算周转量的影响滞后1期且具有长期的正向作用,滞后的原因是消费的滞后性引起,本期收入的增加并不会立刻产生新的交通运输需求;对自身的冲击在第1期最大,导致人均GDP增长2.59%,随后冲击作用递减,在第15期趋于收敛为1.96%,说明人均GDP的外生冲击(如突然增加的投资)具有长期经济增长效应;对交通网络里程的冲击在前3期为负值,但处于递增状态,第4期的影响转为正向,且在第15期导致交通网络里程增长率趋向于收敛为1.14%,本文认为是由于我国采用积极的财政政策,经济衰退时倾向于实行大规模基础设施建设,而经济过热时往往减少基础设施建设,导致两者呈负相关关系,因此正向冲击导致交通网络里程增长率在短期表现为负③,但长期而言,将促进交通网络里程增长。
来自交通网络里程的一个标准差大小的随机冲击,对换算周转量的影响在第1期时为0,然后先递增后递减,在第3期导致换算周转量增长率达到最大值1.33%,并在第15期趋向于0.05%,这说明交通基础设施供给增加一定程度上促进了交通运输需求,虽然第1期时增加了交通网络,但完整被使用是发生在第2期之后,所以在第2~3期对换算周转量的影响最大,但随着交通运输需求得到满足,冲击作用衰减;对人均GDP的影响先为负后为正,在第9期开始产生了较小的正向影响,并在15期使得人均GDP增长率趋向于0.043%,上面已分析了两者间呈现负相关关系,同样可解释为什么正向的交通网络里程冲击导致人均GDP增长率在短期内为负,但正如Kamps(2005)指出“经济增长率对基础设施冲击的长期响应是正向的,但作用较小”[3];对其自身的冲击致使增长率第1期达到了最大值9.77%,随后快速递减,在第15期后趋向收敛于0.038%,表明对自身的冲击没有长期效应。
(五)方差分解
方差分解描述VAR模型中的每一个内生变量的冲击强度(方差)占某个变量总变化的比值。本文通过蒙特卡洛模拟法模拟2000次得到方差分解的结果,如图3所示。
关于换算周转量变化的相对贡献率。第1期主要来源于自身的冲击强度,贡献率为100%,随着时间推移而降低,在第15期,趋于稳定在29.38%。来自人均GDP的冲击强度的相对贡献率在第1期为0,随着时间推移逐渐变大,在第15期后,稳定在11.98%。来自交通网络里程冲击强度的相对贡献率在前4期相对较小,随着时间推移逐渐递增,第15期后,趋于稳定在58.63%。这说明,换算周转量的长期变化可由其自身、人均GDP和交通网络里程来解释,但交通网络里程变化是最重要的影响因素。
关于人均GDP变化的相对贡献率。主要是自身的冲击对其产生影响,在第1期的贡献率最大为81.49%,在第15期后,相对贡献率趋于稳定在77.18%。来自换算周转量的冲击强度对人均GDP变化的相对贡献率在第1期为18.51%,先递减后递增,在第15期后,相对贡献度分别稳定在18.32%。来自交通网络里程冲击强度的相对贡献率在第1期为0,然后先递增后递减,在第15期后,稳定在4.50%。这说明,人均GDP的变化主要来源于自身和换算周转量,交通网络里程的贡献较小。
关于交通网络里程变化的相对贡献率。来自换算周转量的冲击强度的相对贡献率在第1期为1.66%,随着时间先递增后递减,在第15期后,稳定在18.34%;来自人均GDP的冲击强度的相对贡献率在第1期为最大19.50%,随时间推移递减,在第15期后,稳定在2.62%;来自自身冲击强的相对贡献率在第1期为78.82%,随着时间推移先递减后递增,在第15期后稳定在79.03%。这说明,长期而言交通网络里程变化主要由换算周转量和自身来解释,但人均GDP的作用较小。

图3方差分解结果
四、结论与政策
采用以VAR模型为基础的Johansen协整检验方法对我国1980-2016年的人均GDP、交通网络里程与换算周转量的长期与短期的关系进行了实证检验,通过VAR模型最优滞后阶数检验和Johansen协整检验的结果,本文选择VAR最优滞后阶数为3阶,在此基础上,估计出VEC模型,分析了三者的长期和短期关系,在平稳性检验的基础上进行了脉冲响应分析和方差分解。
研究发现:①长期均衡时,人均GDP、交通基础设施对换算周转量的弹性分别为0.521和0.512。②短期波动时,换算周转量的增长率显著受到滞后1期的自身增长率、滞后1期人均GDP增长率,及滞后1~2期的交通网络里程增长率的正向影响;人均GDP增长率显著受到滞后1~2期换算周转量增长率、滞后1期人均GDP增长率的正向影响,但与滞后1-2期的交通网络里程增长率负相关;交通网络里程增长率显著受到滞后2期换算周转量增长率的正向影响,表明我国交通基础设施建设具有较强的外生性。三个变量偏离了长期的均衡状态时,系统均进行反向调整。③脉冲响应分析表明,来自换算周转量的随机冲击对自身的冲击程度较小且不具有长期效应,对经济增长具有长期效应,对交通网络里程具有短期影响;来自人均GDP的随机扰动对换算周转量的影响滞后1期且具有长期正向效应,对自身具有长期效应,对交通网络里程的短期影响为负但长期影响为正;来自交通网络里程的随机冲击对换算周转量短期内产生先递增后递减的正向影响,对人均GDP的短期影响为负但长期影响为正。④方差分解显示,换算周转量自身、人均GDP和交通网络里程均对换算周转量变化的相对贡献率起到了作用;人均GDP的变化主要来源于自身和换算周转量,交通网络里程对人均GDP变化的贡献较小;交通网络里程变化主要由换算周转量和自身来解释,但人均GDP的作用较小。
根据本文实证结论并结合我国交通运输发展现状,提出以下几点政策建议:①交通基础设施投资保持在一定规模。虽然交通基础设施建设对人均GDP增长的影响较低,但可有效促进旅客周转量和货物周转量,而周转量对人均GDP增长具有长期效应。当前我国的交通网络密度(无论是按人均还是面积来计算)仍落后于发达国家和部分发展中大国(如巴西)。因此,保持一定水平的交通基础设施投资规模,提高要素和产品流动性,对经济增长具有间接的促进作用。②交通基础设施的建设重点转移到西部地区。换算周转量的增长率显著受到滞后1~2期的交通网络里程的影响,表明我国整体上交通运输供给水平依然落后于交通运输需求,特别是东西部地区的交通网络密度存在较大的差异,西部地区交通运输需求受到了交通基础设施存量的抑制,进而制约着西部地区的经济发展。因此,交通基础设施的建设重点转移到西部地区。③交通基础设施投资决策需要转换目标,从推动经济增长转向满足区域交通运输需求。交通网络里程增长仅受到滞后2期换算周转量增长率的正向影响,表明我国交通基础设施建设具有较强的外生性,主要由各级政府为实现经济增长来推动,但这样可能导致重复建设且效益较低,无法有效实现资源的有效配置(周黎安,2004)。因此,需要提高投资决策的科学性,依据供求关系来制定规划满足区域交通运输需求。
注释:
①考虑定期航班航线里程包含国内外里程,且运输量较小,本文没有把航线里程包含在内。
②参考山西统计局的统计指标解释,http://www.stats-sx.gov.cn/tjsj/tjnj/nj2015/html/zb15.htm。
③这看似与我国交通网络里程一直处于增长状态的情况不符合,之所以呈现为负,是因为我们假设其他的条件不变下(如换算周转量不变)来分析,仅仅来自人均GDP外生冲击的影响,而现实的情况是,交通网络增长不仅仅受到经济增长的影响,还受到其他因素的影响,所以现实为正。
