25t轴重米轨铁路轨道结构设计
2018-09-14杨明辉
张 凯,杨明辉
(中铁二院工程集团有限责任公司,四川成都 610031)
玻利维亚现有铁路分为西部线(安第斯线)和东部线,向东连接巴西,向西连接秘鲁和智利,如图1所示。中间缺少约400 km铁路将两侧联通起来,玻利维亚政府希望该铁路的连通能满足沿线地区农业和矿产的运输需求,带动区域经济发展。作为填补400 km铁路的第一步,玻利维亚政府计划首先修建Montero(蒙特罗)至BuloBulo(布落布落)的铁路,线路全长148 km,主要技术要求为米轨轨距(1 000 mm)、预应力混凝土轨枕碎石道床、列车轴重25 t、最高运行速度100 km/h。
此工况下轨道结构设计尚无规范可循、无经验可借,必须对米轨铁路轨道结构设计进行力学校核分析,力求获得最优的轨道结构形式,使其在预定的使用期限内以及在规定的使用条件下,保持良好的线路状态,既确保列车的安全,又保证项目建设的经济性。
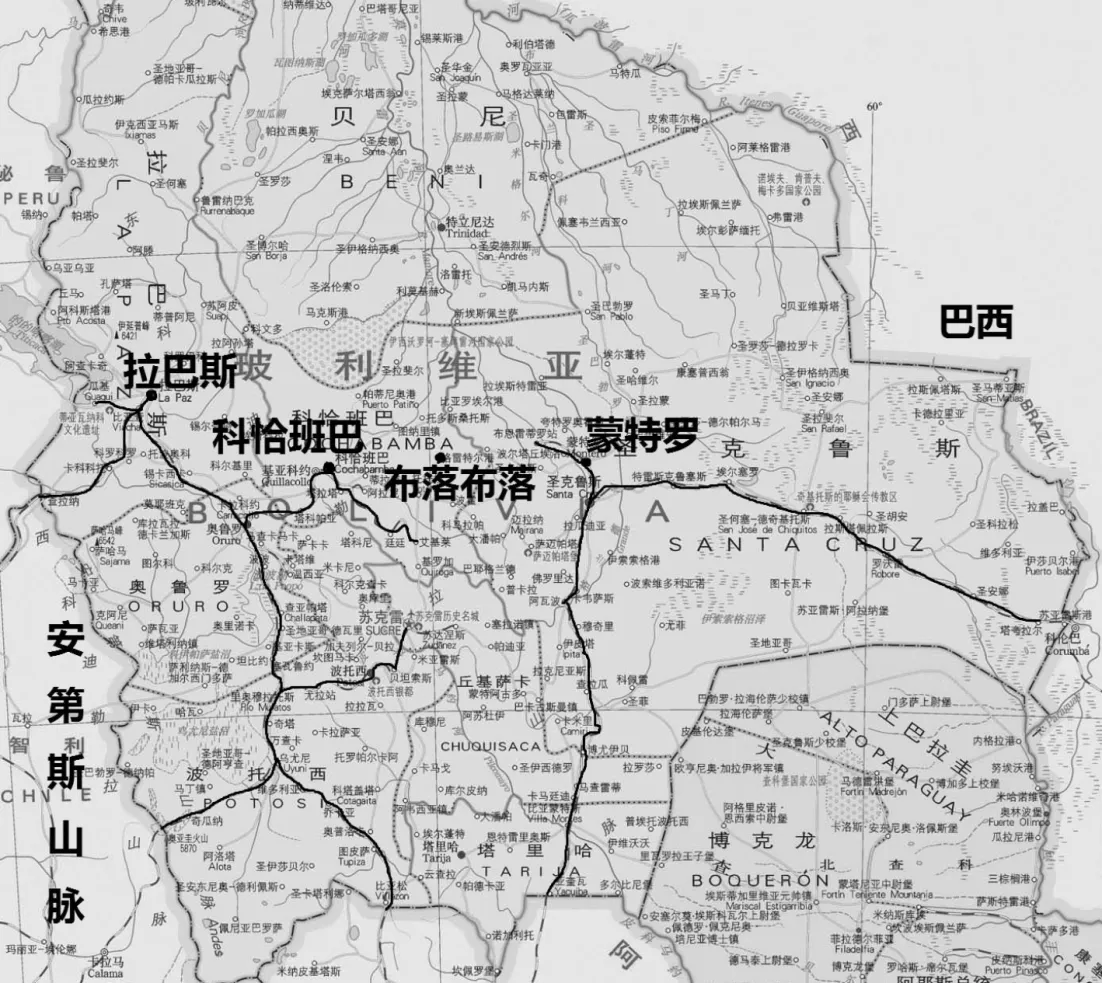
图1 玻利维亚现有铁路概况
1 轨道结构强度的检算方法
1.1 计算模型
由于轨道钢轨的抗弯刚度很大,而轨枕布置相对较密,这样就可近似地把轨枕的支承看作是连续支承,简化为图2所示的连续支承梁模型,从而进行解析性的分析。
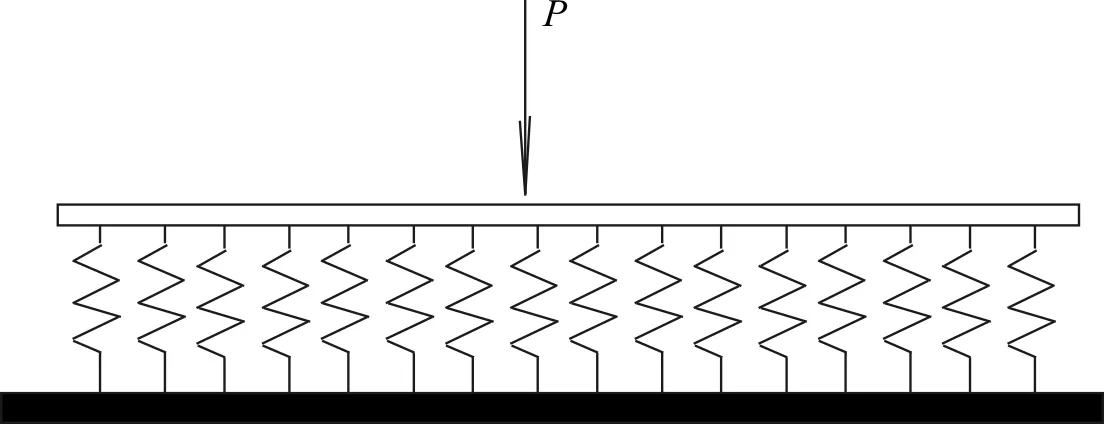
图2 连续支承梁模型
该模型最初是由德国E.Winkler(1867)提出的,后由德国A.Zimmermann、美国A.N.Talbot等所改进和完善。该法所求得的解析解是严密的理论解,可将轨道的内力和变形分布写成函数的形式,应用起来既简单方便又直观,这一经典理论至今仍具有重要的理论和应用价值,现在世界各国和中国铁道标准均采用这一模型。
1.2 基本假设
(1)轨道和车辆均处于正常良好状态,符合有关的技术标准。
(2)钢轨视为支承在弹性基础上的等截面无限长梁;轨枕视为支承在连续弹性基础上的短梁。基础或支座的沉落值与它所受的压力成正比。
(3)轮载作用在钢轨的对称面上,且两股钢轨的载荷相等,基础刚度均匀且对称于轨道中心线。
(4)不考虑轨道本身的自重。
1.3 计算载荷
车辆的一个车轮压在钢轨计算截面上,除了该车轮对计算截面产生应力、挠度外,还应考虑邻轮的影响。一般地讲,当车轮距计算截面5 m以上时,这种影响可以略去不计。由此可知,轮位相对于计算截面排列不同,则其所产生的钢轨弯矩M0、钢轨下沉y0和枕上压力R0也各不相同,其中必有一种排列的某一轮子放在计算截面,产生的M0、y0和R0为最大,这种排列的轮位称为最不利轮位。
通常车辆的转向架间距离超过5 m,故不考虑各转向架的相互影响。各轮载及转向架各轴间距均相同,故只需取第一转向架进行计算。又考虑到常规车辆转向架为两轴式,故取第一转向架第一轮位进行计算,其它各轮位的轮下计算截面计算值与之相同。
2 钢轨受力检算
2.1 钢轨弯矩和枕上压力计算
(1)计算公式
静止车轮系作用下钢轨弯矩M0、枕上压力R0,根据连续支承梁模型,可以列出弹性基础钢轨挠曲线方程:
(1)
式中:M为钢轨弯矩;E为钢轨弹性模量;I为钢轨断面水平惯性矩;dx为钢轨截面沿线路方向的位置变量的微分;dy为钢轨计算截面的垂向挠度值的微分;
由式(1),根据均匀连续弹性基础理论和力的独力作用原理,可得静止车轮系作用下钢轨弯矩M0、枕上压力R0的计算式为:
(2)
式中:k为钢轨基础弹性模量与钢轨弯曲刚度的相对比值;a为轨枕间距;P0i为作用于钢轨上的各车辆车轮静重;μi、ηi为连续弹性基础上等截面无限长梁的影响线系数,μi=e-kx(coskx-sinkx),ηi=e-kx(coskx+sinkx)。不同轮位距计算截面的距离各不相同,因而各有不同的μi和ηi,如图3所示。
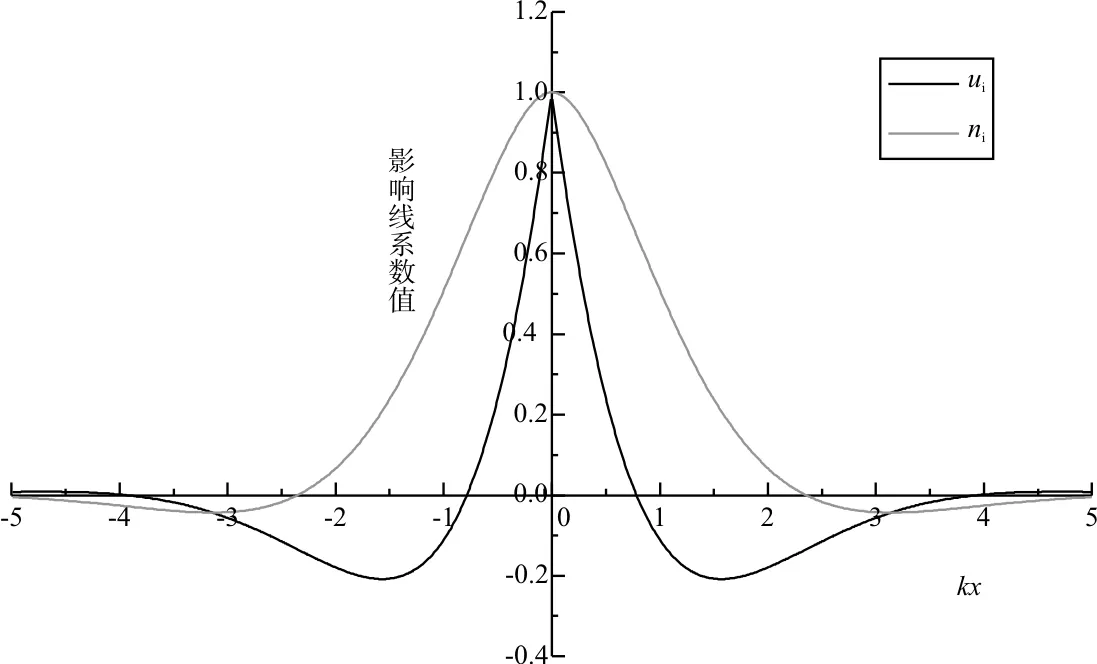
图3 影响线系数曲线
u=D/a
(3)
式中:D为钢轨支点弹性系数,参照《铁路轨道设计规范》重型、特重型轨道类型取值为27 200 N/mm;a为轨枕间距。
(2)计算参数
根据玻利维亚铁路情况,一般钢轨型号的选取在60 kg/m、54 kg/m钢轨及43 kg/m之间,因此下面计算着重比较以上三种钢轨类型对钢轨应力的影响。从节约投资成本的方面去考虑,选取尽量大的轨枕间距,即每公里尽量减少铺设轨枕的根数,但是同时又要满足轨道结构的强度检算,根据经验暂取每公里铺设1 680根轨枕进行计算,然后再调整轨枕间距进行检算。
为计算钢轨受力的最不利情况,选取计算车辆轴重25 t,车速为100 km/h工况进行计算。表1为静止车轮系作用下钢轨弯矩M0、枕上压力R0的计算参数,表2为计算结果。
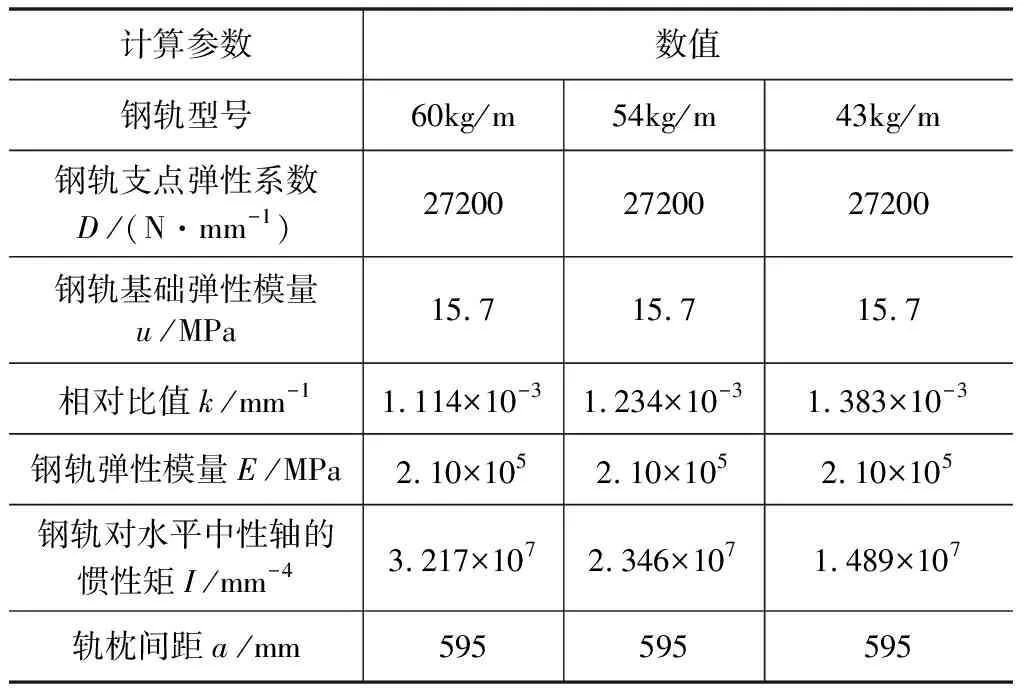
表1 静止车轮系作用下计算参数
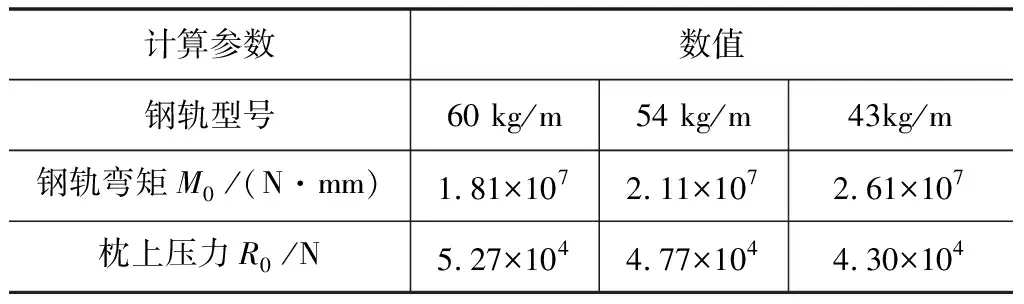
表2 静止车轮系计算结果
(3)最大钢轨弯矩Md和枕上压力Rd
在考虑速度、曲线偏载系数后,钢轨弯矩、枕上压力的最大值可得:
Md=(1+α+β)M0
Rd=(1+α+β)R0
(4)
式中:α、β为速度、曲线偏载影响因子。根据《铁路工程设计技术手册-线路》,计算钢轨弯曲应力时,车辆的速度影响系数α按下式计算:
(检算钢轨用)
(5)
当计算轨下基础各部件载荷及应力时,应当乘以0.75的折减系数,则车辆的速度影响系数α按下式计算:
(检算轨下各部件用)
(6)
取其未被平衡欠超高最大值为Δh=50 mm,米轨钢轨中心距S=1078 mm,故曲线偏载系数β为:
(7)
根据公式(4),最大钢轨弯矩Md、枕上压力Rd计算结果见表3。
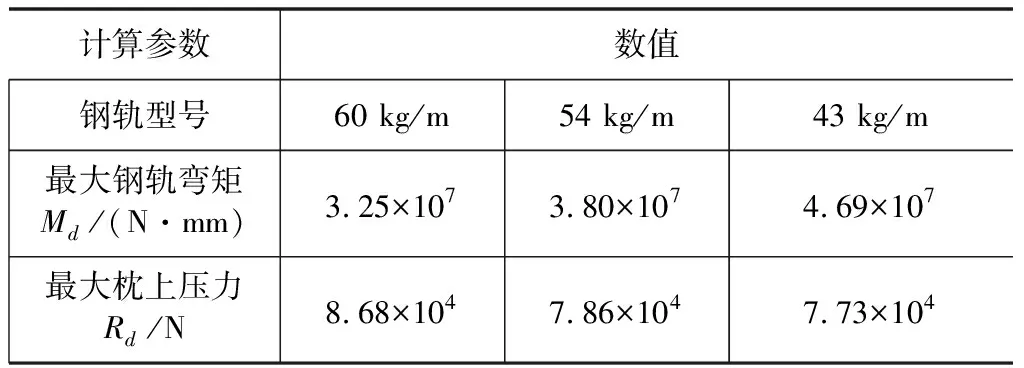
表3 最大弯矩及枕上压力计算结果
2.2 钢轨应力计算
钢轨应力的计算公式为:
(8)
式中:δ头d、δ底d为轨头、轨底边缘动弯应力最大可能值;W头、W底为钢轨头部、底部对水平中性轴的截面模量;f为横向水平力系数,据调查玻利维亚铁路最小半径为500 m,则横向水平力系数取1.7。
根据钢轨强度检算公式:
σd+σt+σf≤[σ钢轨]
(9)
式中:σf为制动附加应力,取σf=10 MPa;σt为温度附加力,对于有缝线路σf=0;σ钢轨为钢轨容许应力,取材质为U71Mn的钢轨容许应力352 MPa。由以上各式可以算出钢轨最大应力(表4)。
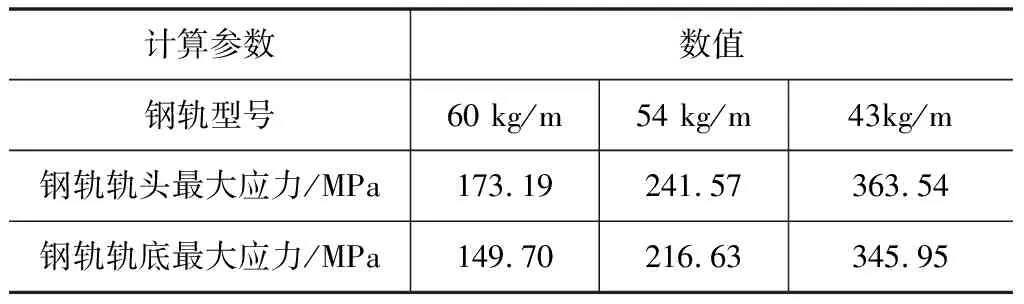
表4 钢轨最大应力计算结果
由表4可知,在本项目工况下,选取43 kg/m型钢轨通不过钢轨强度检算,选取60 kg/m型钢轨以及54 kg/m型钢轨可以通过强度检算,但是考虑到项目经济性,因此,建议玻利维亚铁路选用54 kg/m型钢轨,以下检算轨道其他部件时均采用54 kg/m型钢轨的参数。
3 混凝土轨枕弯矩检算
对于混凝土轨枕,计算轨枕弯矩时把它视为支承在弹性基础上的短梁,分别取最不利支承图式进行计算,当计算轨下截面正弯矩Mg时,假定轨枕中间部分完全掏空,道床支承方式如图4(a)所示,当计算枕中截面负弯矩Mc时,道床支承方式如图4(b)所示,反映了轨枕枕中道砟满铺,中间截面负弯矩最为不利,表5为轨枕弯矩检算结果。
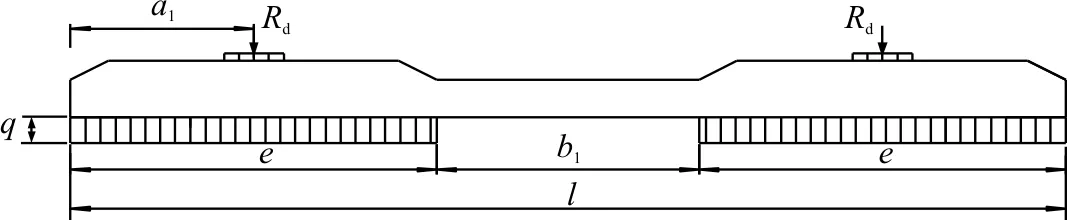
(a)轨下截面
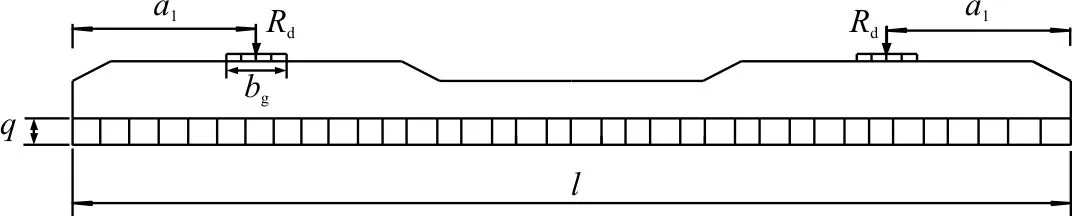
(b)枕中截面图 4 轨枕弯矩检算
轨枕弯矩计算公式为:
(轨下截面)
(10)
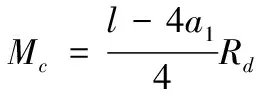
(11)
式中:a1为荷载作用点至枕端距离;e为单股钢轨下,轨枕的全支承长度,假定中部掏空156.4 mm,则e=921.8 mm;bg为轨下衬垫宽度,一般取轨底宽;l为轨枕长度;根据玻利维亚铁路米轨轨枕设计计算书数据,其轨下截面允许弯矩为15.07×106N·mm,中间截面允许弯矩为-11.06×106N·mm,由表5可知,轨枕弯矩检算通过。

表5 轨枕最大弯矩计算结果 N·mm-1
4 道床顶面应力计算
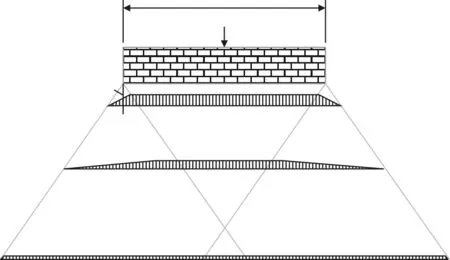
道床顶面的应力,无论是沿轨枕纵向还是横向,分布都是不均匀的。其压力分布如图5所示。

图 5 道床顶面应力分布图
道床顶面上的平均压应力为:
(12)
考虑到实际应力分布的不均匀性,道床顶面上的最大压应力为:
σbmax=mσb
(13)
式中:b为轨枕底面宽度,混凝土枕取平均宽度;m为应力分布不均匀系数。
由以上各式可以得到道床顶面最大应力的计算结果,详见表6。

表6 道床顶面最大应力计算结果
根据《铁路轨道强度检算法》,对于碎石道床,道床容许应力取0.5 MPa,由表可知,道床顶面最大应力满足条件,可以通过检算。
5 路基基床表层应力计算
根据玻利维亚铁路情况,为了节约投资成本,因此下面计算着重比较不同道床厚度对基床表层应力的影响。假定道床顶部压力在道床内按φ角向下扩散到路基顶面,如图6所示。
轨枕横向及纵向的压力扩散线交点分别为k1、k2,距枕底高度分别为h1、h2。
h1、h2按下式计算:
(14)
(15)
式中 :φ为压力扩散角,根据《路工务技术手册》,碎石道床φ=35°。
根据上式可计算出:
h1=171.38 mm、h2=658.23 mm
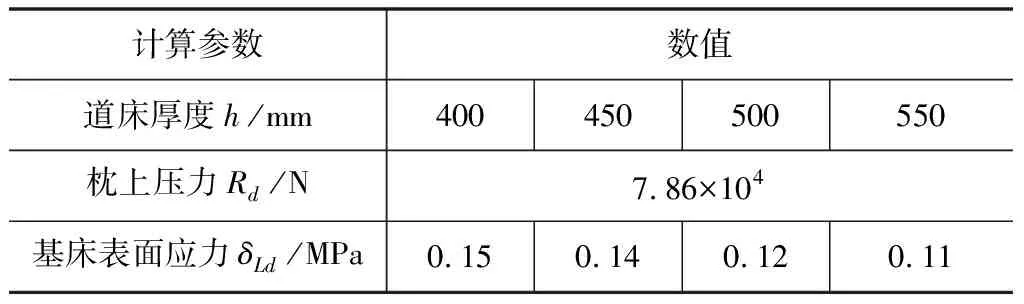
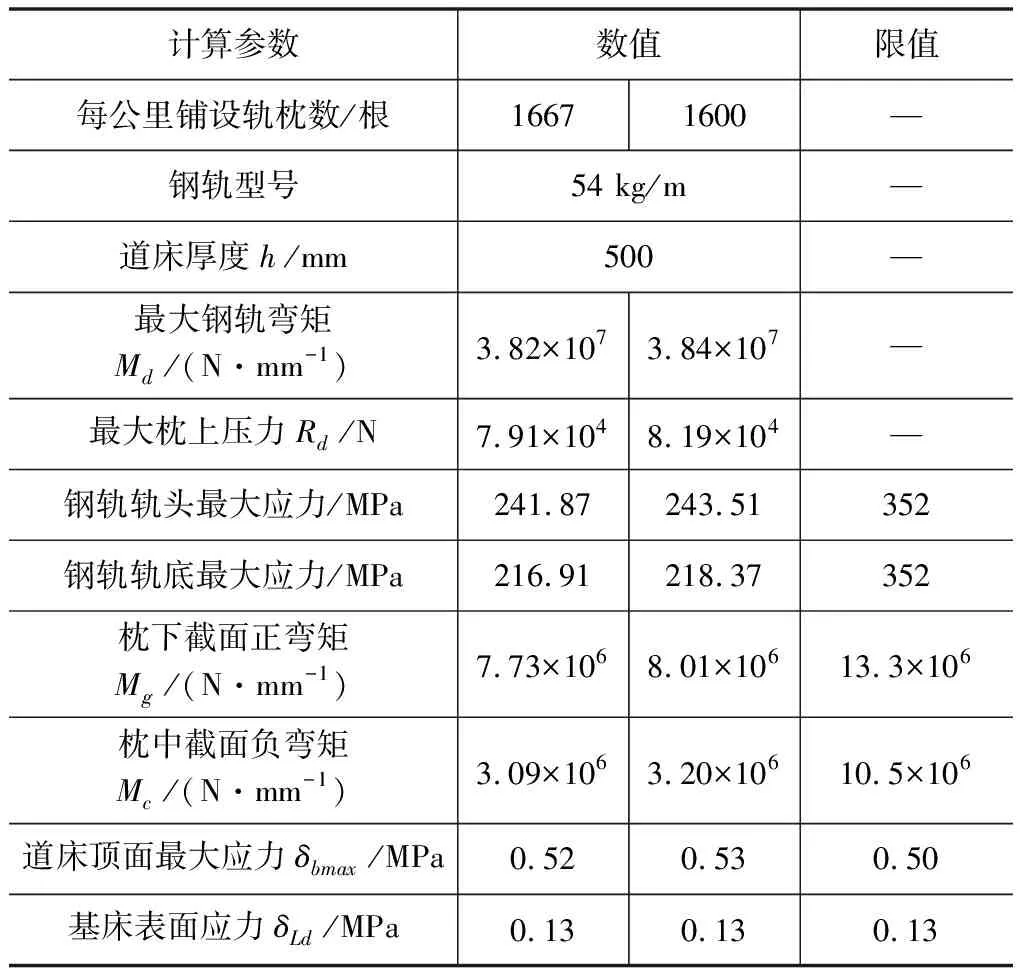
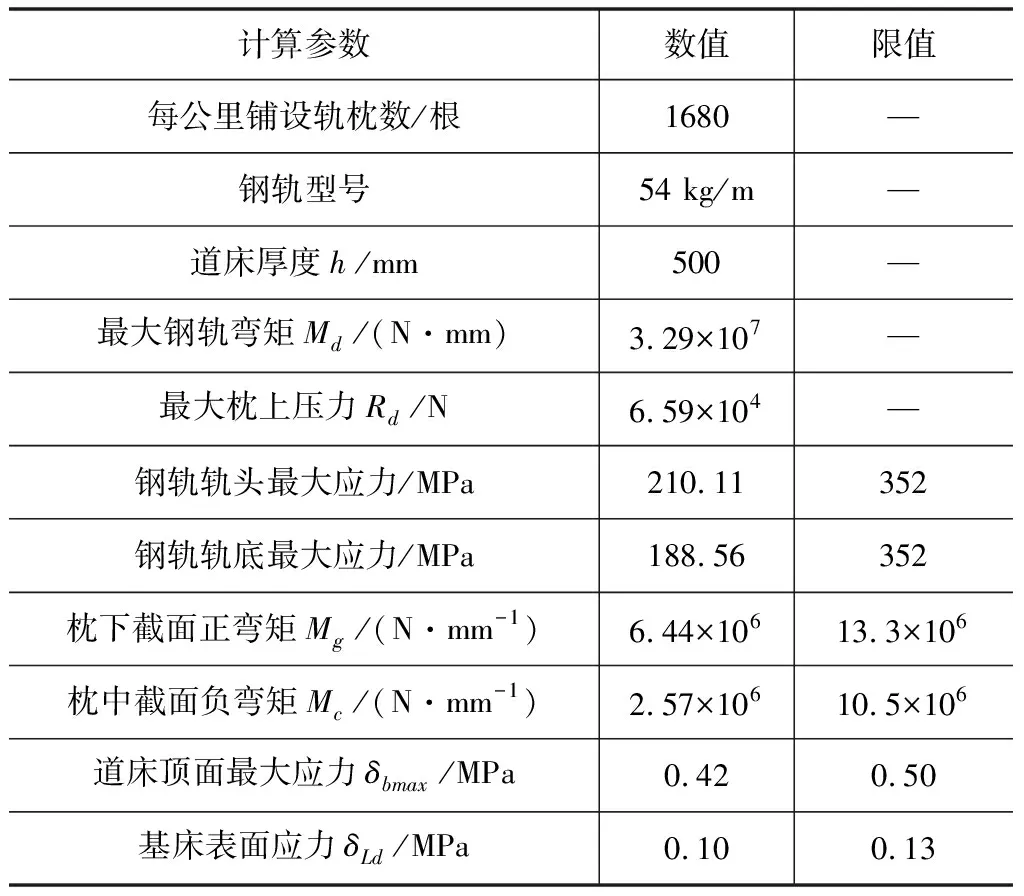
当道床厚度h1 (16) 式中:δLd为路基基床表面应力(MPa);h为道床厚度(mm)。 (a) (b)图 6 道床应力传递示意 轨枕横向及纵向的压力扩散线交点分别为k1、k2,距枕底高度分别为h1、h2。 h1、h2按式(17)计算: (17) (18) 式中 :φ为压力扩散角,根据《路工务技术手册》,碎石道床φ=35°。 根据式(17)、式(18)可计算出: h1=171.38 mm、h2=658.23 mm 当道床厚度h1 (19) 式中:δLd为路基基床表面应力(MPa);h为道床厚度(mm)。 故路基基床表面应力计算结果见表7。 表7 不同道床厚度下路基基床表面压应力 根据《铁路轨道强度检算法》,新建线路路基表面允许承压应力为0.13 MPa,由表7可知,道床厚度为400 mm和450 mm时不能通过基床表层应力检算,道床厚度为500 mm和550 mm可以通过基床表层应力检算,但考虑工程造价的问题,建议玻利维亚铁路道床厚度设计为500 mm(面砟300 mm,底砟200 mm)。 由以上计算过程可知,在轴重25 t、运行速度100 km/h时,采用54 kg/m型钢轨、1 680 根/km、道床厚度500 mm时,轨道结构可以通过强度检算。根据本文计算可知,钢轨型号以及道床厚度已经采用较低标准,如果再降低标准将通不过轨道强度检算,但是轨枕间距还有可以调整的余地,因此本节将增大轨枕间距进行计算,以期获得最优的轨道结构形式。 本文已经计算过轨枕按1 680 根/km布置时的轨道结构强度,下面检算不同轨枕间距时的轨道结构强度,表8为不同轨枕间距对轨道结构强度的影响结果。 由表8可知,当每公里铺设轨枕1 667根轨枕或1 600根轨枕时,钢轨最大应力和轨枕弯矩、路基基床表面应力都可以通过强度检算,但是道床顶面最大应力超过了规范规定的限值,因此,建议玻利维亚Montero至BuloBulo铁路项目轨枕每公里按照1 680根铺设。 以上计算检算了车辆25 t轴重、车速100 km/h工况下的轨道结构强度,即货车通过时的工况。如该线有客车运行的需要时,根据以上采用的轨道结构形式检算客车运行时的轨道结构强度,客车计算工况为轴重18 t、最高运行速度160 km/h,表9为检算结果。 由表9可知,当采用客车运行工况的参数进行计算时,采用54 kg/m型钢轨,每公里铺设1 680根轨枕,道床厚度500 mm时,也可以通过轨道结构强度检算,且每项指标都有较大的安全余量,因此,本文采用的轨道结构形式可以满足玻利维亚Montero至BuloBulo铁路项目客货共线运行的需要。 表8 不同轨枕间距下轨道结构强度检算结果 表9 客车运行工况下轨道结构强度检算结果 结合玻利维亚Montero至BuloBulo铁路项目,选取最不利工况,即车辆轴重25 t、速度100 km/h,以及客车轴重18 t、速度160 km/h通过连续支撑梁模型对各种形式的轨道结构进行强度检算。 钢轨强度计算结果分析表明,轨枕间距595 mm时,采用钢轨型号43 kg/m时强度检算不通过,采用54 kg/m及60 kg/m钢轨时可以通过强度检算,建议选用54 kg/m型钢轨。 轨枕弯矩计算结果表明,轨枕间距595 mm时,采用米轨轨枕及54 kg/m型钢轨时可以通过强度检算,并有较大安全余量。 道床顶面应力计算结果表明,轨枕间距595 mm时,采用米轨轨枕及54 kg/m型钢轨时可以通过强度检算。 基床表层应力计算结果表明,道床厚度越大,路基基床表面应力越小,道床厚度500 mm时就可以满足基床表层应力要求。 轨枕间距计算分析表明,增大轨枕间距时,道床顶面应力不能满足限值要求,因此建议轨枕按每公里1 680根布置,通过选取以上参数校核的了客车运行时的轨道结构强度,由计算结果可知,可以满足客车运行的各项指标。 通过以上分析可知,考虑项目建设的经济性,玻利维亚Montero至BuloBulo铁路项目轨道设计可采用UIC54型钢轨,预应力混凝土米轨轨枕按1 680 根/km布置,采用弹条Ⅰ型扣件,道床结构厚度为500 mm(面砟300 mm,底砟200 mm)。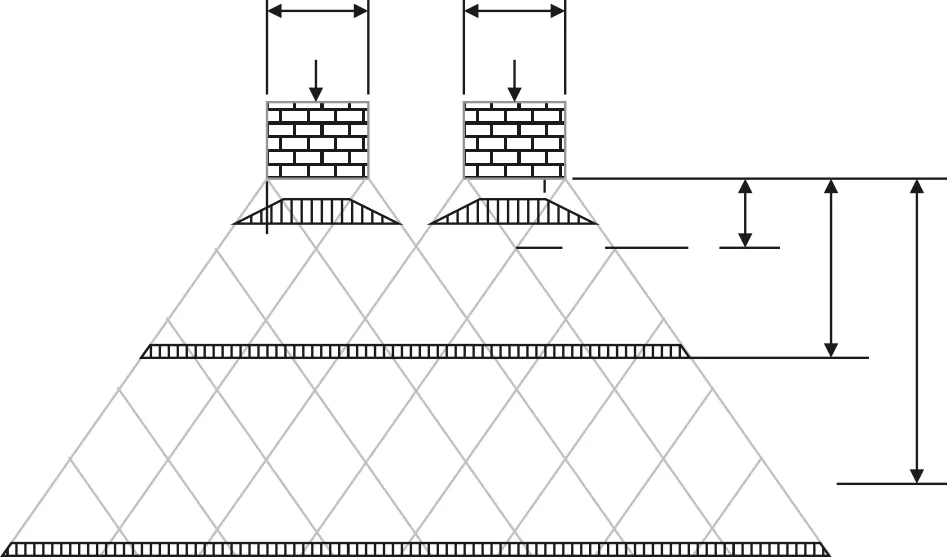
6 比较工况
7 结论
