六自由度机械臂运动学分析与仿真研究

肖俊明, 韩 伟, 王瑷珲, 李继朋, 梁 旺

(中原工学院 电子信息学院，河南 郑州 450007)

20世纪60年代初机器人问世以来，机器人技术逐步取得了实质性的进步与成果[1]，目前已被应用于很多行业，在航空航天、汽车工业、海洋探索、医疗手术等行业的高科技领域发挥着重要作用，促进了人们生活的改善。机械臂是最早应用于实际生产领域的一种机器人[2]。其中，串联机械臂应用最为广泛，它是由若干通过关节连接在一起的连杆组成的具有多个自由度的开链型连杆机构。它的一端固定在基座上，另一端为末端执行器，主要进行抓取操作，中间部分是由若干带驱动的转动或移动关节串联而成的机构体。机械臂运动学研究的是各连杆关节的运动与机械臂各部分(一般为末端执行器)的位置、姿态之间的数学关系。研究这种关系是设计机械臂运动控制器所必需的。机械臂运动学的研究主要有正运动学问题和逆运动学问题两类。由已知机械臂各关节的角度位置和各连杆的长度，计算末端执行器相对基坐标系原点的位置与姿态，即为正运动学问题。要使末端执行器运动到期望的位置与姿态，就必须计算出各关节此时此刻的位置角度，即为逆运动学问题。

传统物理实体设计方法不但费时费力，而且很难达到理想效果。 随着计算机技术的不断发展，通过计算机仿真技术完全能够设计出接近实物且精度较高的机械臂运动模型，经过实际调试达到理想效果，这不仅可缩短设计周期，同时能节省大量生产成本。运用Matlab软件的Robotics Toolbox(即机器人工具箱)，可便捷地完成机械臂的空间运动学建模、分析与仿真及轨迹规划等任务。通过计算机对机械臂建模与仿真，不仅能够得到机械臂各关节运动曲线，而且可直观地显示出机械臂的运动情况，为机械臂的设计提供理论支撑。

1 六自由度机械臂运动学分析

1.1 机械臂D-H坐标系及连杆参数

D-H参数法是Denavit和Hartenberg在1955年提出的，它是为机械臂关节链中每个连杆坐标系建立关系矩阵的一种方法[3-4]。

本文研究对象为六自由度串联型机械臂，该机械臂有6个关节，而且均为转动型。图1所示为六自由度机械臂。图2所示为六自由度机械臂的D-H坐标系。以各关节的中心为坐标系原点建立坐标系，使坐标系{O4}的原点和坐标系{O5}的原点重合，以末端执行器中心为坐标系{O6}的原点，按照D-H参数法确定的机械臂连杆参数如表1所示。

1.2 机械臂正运动学方程

确定全部连杆参数之后，可按照以下步骤建立相邻两连杆i与i-1之间的关系：

(1) 以第i连杆与第i-1连杆的连接轴作为zi-1坐标轴；

(2)xi坐标轴沿zi-1轴和zi轴的公垂线，且指向zi轴而背离zi-1轴；

图1 六自由度机械臂

图2 六自由度机械臂的D-H坐标系

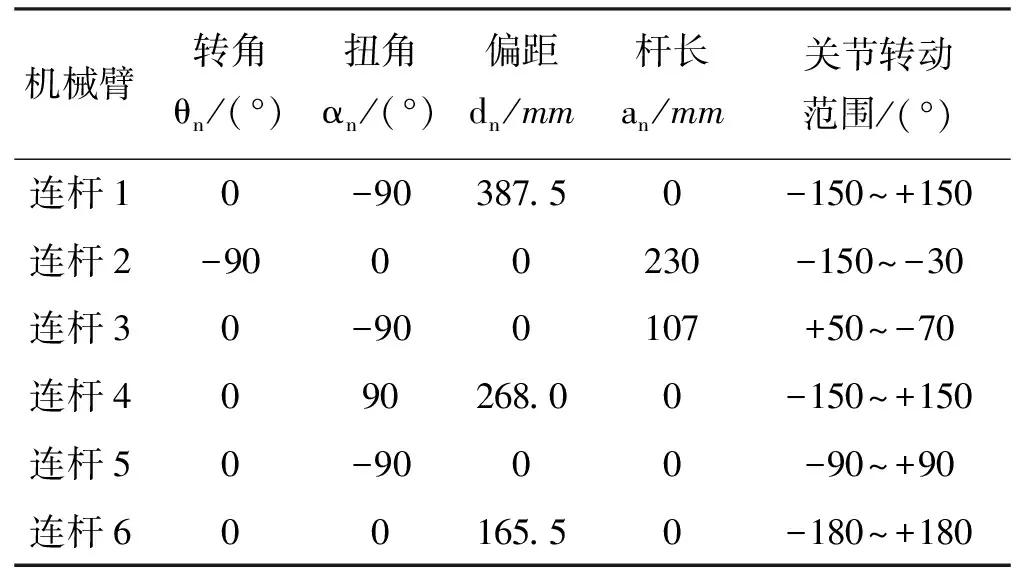
表1 按D-H参数法确定的机械臂连杆参数

(3) 坐标yi轴虽不关键，但其方向必须满足与xi轴、zi轴构成xiyizi右手直角坐标系的条件；

(4) 将xi-1轴绕zi-1轴旋转θi角，使xi-1轴与xi轴同向；

(5) 将坐标系{Oi-1}沿zi-1轴平移距离di，使xi-1轴与xi轴在同一条直线上；

(6) 将坐标系{Oi-1}沿xi轴平移距离ai，使其坐标原点与坐标系{Oi}的原点重合；

(7) 将坐标系{Oi-1}绕xi轴旋转αi角，使zi-1轴与zi轴在同一条直线上。

经上述坐标系变换，得到的齐次变换矩阵为：

i-1Ti=Rot(zi-1,θi)Trans(0,0,di)

Trans(ai,0,0)Rot(xi,αi)

(1)

式中：i-1Ti是坐标系{Oi-1}变换到坐标系{Oi}的齐次变换矩阵；Rot(zi-1,θi)是xi-1轴绕zi-1轴旋转θi角的齐次变换矩阵；Trans(0,0,di)是坐标系{Oi-1}沿zi-1轴平移距离di的齐次变换矩阵；Trans(ai,0,0)是坐标系{Oi-1}沿xi轴平移距离ai的齐次变换矩阵；Rot(xi,αi)是坐标系{Oi-1}绕xi轴旋转αi角的齐次变换矩阵。

由式(1)可推导出：

(2)

将表1中连杆参数代入式(2)，可得到机械臂各坐标系之间转换的齐次变换矩阵。坐标系{O0}到坐标系{O1}的变换矩阵为：

(3)

坐标系{O1}到坐标系{O2}的变换矩阵为：

(4)

坐标系{O2}到坐标系{O3}的变换矩阵为：

(5)

坐标系{O3}到坐标系{O4}的变换矩阵为：

(6)

坐标系{O4}到坐标系{O5}的变换矩阵为：

(7)

坐标系{O5}到坐标系{O6}的变换矩阵为：

(8)

因此，机械臂的正运动学方程为：

(9)

式中：n=[nxnynz0]T是坐标系{O0}相对于坐标系{O6}在x轴上的方向矢量；o=[oxoyoz0]T

是坐标系{O0}相对于坐标系{O6}在y轴上的方向矢量；a=[axayaz0]T是坐标系{O0}相对于坐标系{O6}在z轴上的方向矢量；p=[pzpypz1]T是坐标系{O0}相对于坐标系{O6}的位置矢量。

式(9)表示的是末端执行器的位姿与基坐标系原点之间的变换关系。取初始位姿：d1=375.5 mm,d4=268.0 mm,d6=165.5 mm,a2=230.0 mm,a3=107.0 mm,θ1=θ3=θ4=θ5=θ6=0，θ2=-90°，代入式(9)后得到的机械臂初始位姿矩阵为：

(10)

这与机械臂处于初始位姿的实际情况完全一致，说明所得机械臂正运动学方程是正确的。

1.3 机械臂逆运动学方程

根据机械臂正运动学方程，可对机械臂求逆解。

关节1转角为：

θ1=arctg-1[(-px+d6·ay)/(-px+d6·ax)]

(11)

关节2转角为：

θ2=arctg-1{[(px12+py12)1/2·(-d4c3-a3s3)-pz1·(-d4s3+a3c3+a2)]/[(px12+py12)1/2·(-d4s3+

a3c3+a2)+pz1·(-d4c3-a3s3)]}

(12)

关节3转角为：

(13)

关节4转角为：

θ4=arctg-1{[-(ax·s1-ay·c1)]/[-(ax·c1c23+ay·s1c23-az·s23)]}

(14)

关节5转角为：

θ5=arctg-1{[az·s23c4-ax·(c1c23c4+s1s4)-ay·(s1c23c4-c1s4)]/(-ax·c1s23-ay·s1s23-az·c23)}

(15)

关节6转角为：

θ6=arctg-1{[nz·s23s4-nx·(c1c23s4-s1c4)-ny·(s1c23s4+c1c4)]/[oz·s23s4-ox·(c1c23s4-s1c4)-

oy(s1c23s4+c1c4)]}

(16)

式中：px1=c1·(-d4·s23+a3c23+a2c2)；

py1=s1·(-d4s23+a3c23+a2c2);

pz1=-d4c23-a3s23-a2s2；

sij=sin(θi+θj)；

cij=cos(θi+θj)；

si=sinθi；

ci=cosθi。

2 机械臂工作空间仿真分析

机械臂的工作空间是指机械臂的特定部位(一般为末端关节坐标系原点)在一定条件下所能达到的空间位置集合[5-6]。工作空间的大小反映了机械臂的活动范围。机械臂的设计工作空间是一个重要的运动学指标。本文运用蒙特卡罗法[7-8]对机械臂的工作空间进行仿真分析。

蒙特卡罗法的应用步骤和算法流程如图3所示。

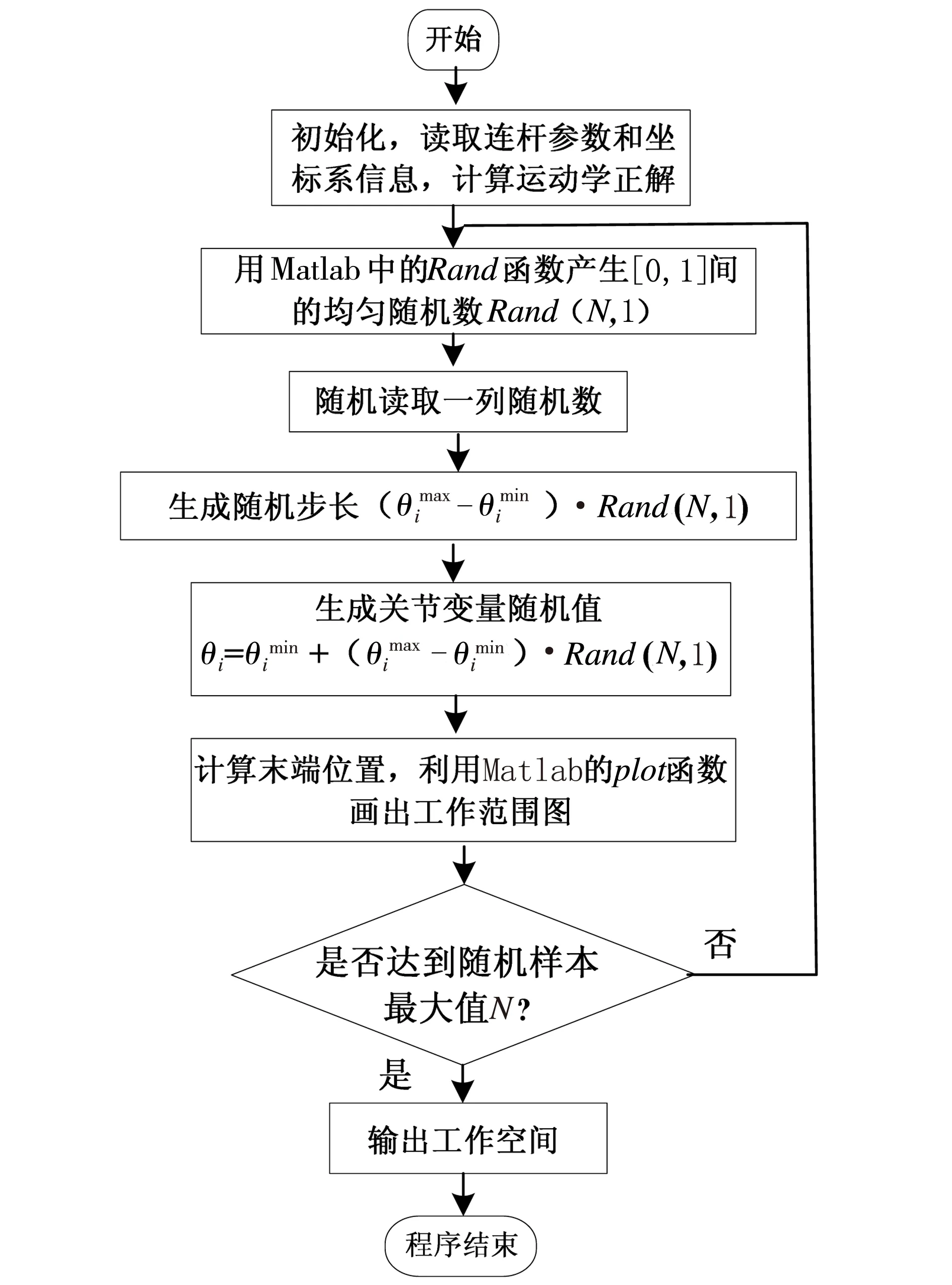
图3 机械臂工作空间的仿真算法流程

首先初始化，读取连杆参数和坐标系，求解机械臂的正解，并根据正解得出机械臂末端在基坐标系中的位置向量；然后利用Matlab软件中的Rand函数产生[0，1]间的均匀随机数Rand(N,1)，并读取一列随机数。

则各关节的随机值为：

(17)

本文结合该机械臂模型的实际参数，取N=12 000，打印出了机械臂工作空间及其在空间3个坐标平面上的投影(见图4)。

为了对计算出的机械臂工作空间进行验证，可任取一关节角度向量q，并令：

q=[-pi/2-pi/2pi/3pi/2pi/3pi/3]

(18)

代入式(9)可得：

px=-143.327 4 mm,py=-268.039 7 mm,pz=367.241 6 mm。显然，所得坐标在机械臂末端工作空间内。

同理，可取规定范围内不同的θi值，再次验证机械臂末端位置，所得位置也在此工作空间内。因此，利用蒙特卡罗法计算机械臂末端工作空间是可行的。

(a) 机械臂末端运动空间的三维空间范围

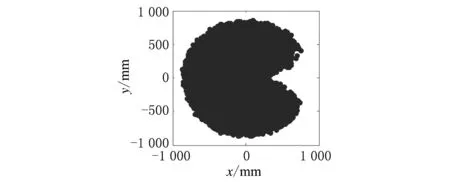
(b) 末端运动空间在xOy坐标平面上的投影

(c) 末端运动空间在xOz坐标平面上的投影

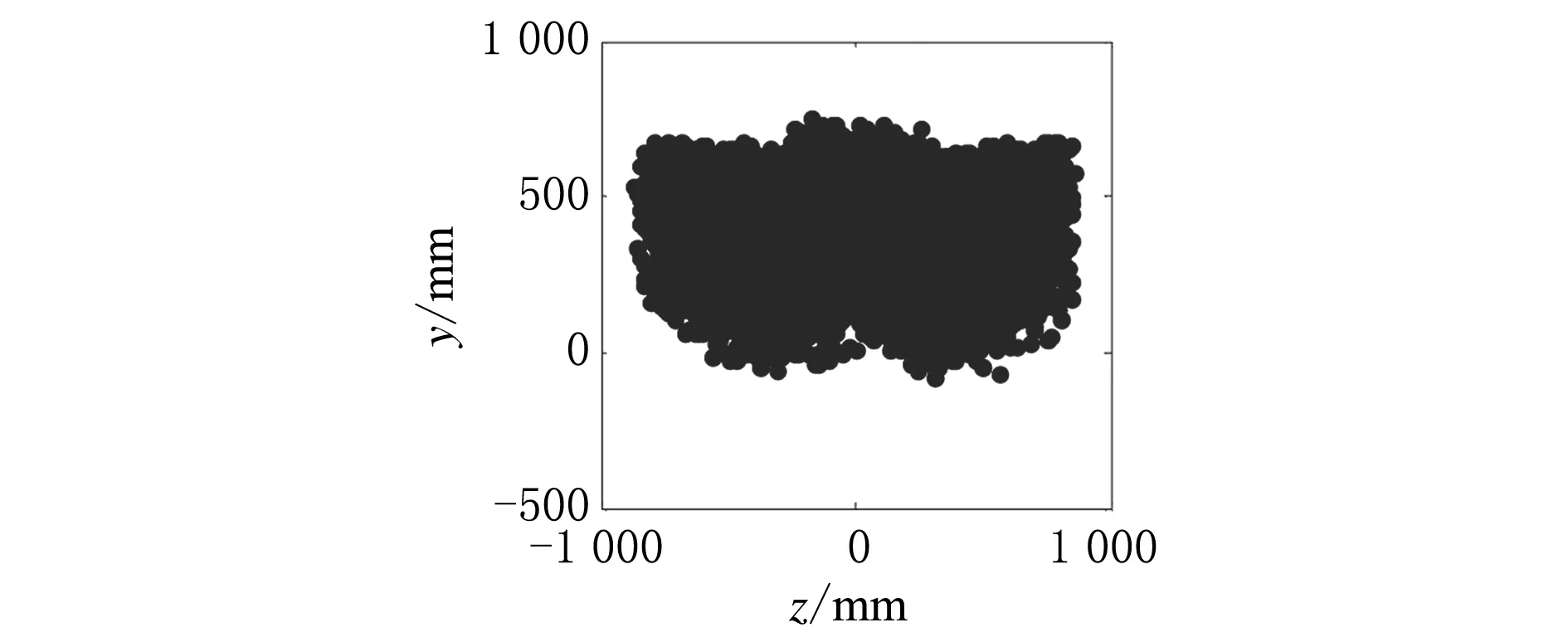
(d) 末端运动空间在yOz坐标平面上的投影图4 机械臂末端工作空间及其在坐标平面上的投影

3 正、逆运动学仿真分析

3.1 仿真模型的建立

机器人工具箱是由澳大利亚科学家Peter Corke开发的一套基于Matlab软件环境的机器人学工具箱[9]。在Matlab系统环境下，借助Robotics Toolbox可以便捷地建立机械臂仿真模型(见图5)。

建立机械臂仿真模型时调用link函数的格式为：

Li=link([αiaiθidisign],‘standard’)。

式中:αi为连杆扭角;ai为连杆长度;θi为关节转角;di为偏置距离;sign=0；standard为标准D-H参数。

在图5(a)中，拖动横条上的小方块，则相应的关节转动。

机械臂建模程序如下：

L1=link([-pi/200387.50],‘standard’);

L2=link([0230-pi/200],‘standard’);

L3=link([-pi/2 107000],‘standard’);

L4=link([-pi/2002680],‘standard’);

L5=link([pi/20000],‘standard’);

L6=link([000165.50],‘standard’);

r=robot({L1L2L3L4L5L6},‘六自由度机械臂’);

plot(r,[0-pi/20000])；

drivebot(r)；

(a) 模型的驱动器

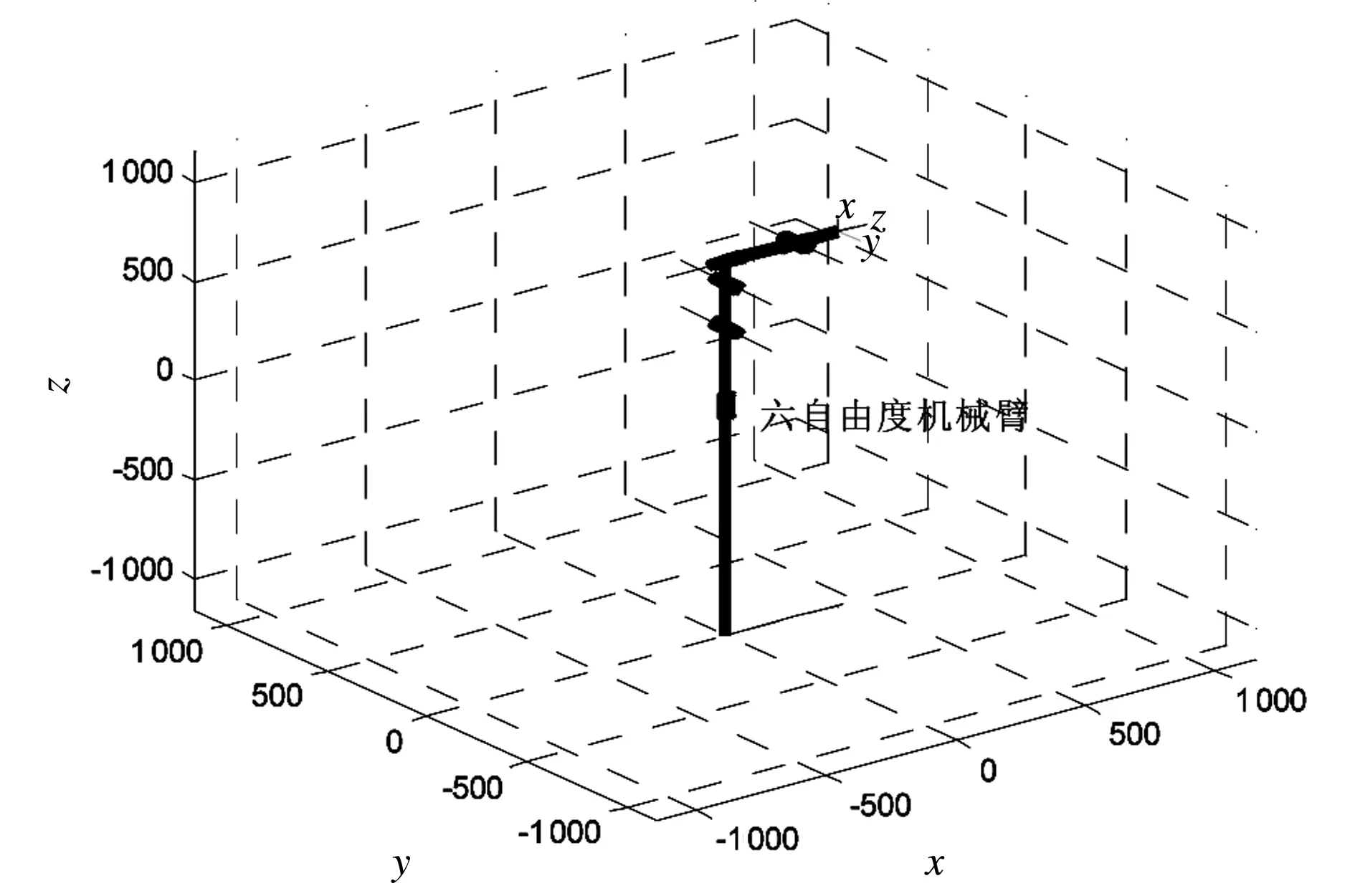
(b) 模型的初始状态图5 机械臂仿真模型

3.2 机械臂正、逆运动学方程验证

在Matlab的Robotics Toolbox中，利用fkine函数可实现机械臂正运动学方程求解。调用fkine函数的格式为：T=fikine(robot,q)。其中:robot为所建机械臂模型；T为q所定义的每个前向运动的正解变换矩阵。

为验证运动学方程式(9)的正确性，现结合该机械臂的实际情况，随机取工作空间中一点Q1的关节角度向量q=[-pi/2-pi/2pi/3pi/2pi/3pi/3],通过fkine(robot，q)函数得到该点相对基坐标原点的变换矩阵如下：

(19)

将关节角度向量q代入式(9)，其计算结果与式(19)结果一致，从而验证了机械臂正运动学方程的正确性。

同理,可利用Robotics toolbox中的ikine函数实现机械臂逆运动学的求解。调用ikine函数的格式为：q′=ikine(robot，T′，q0，M)。其中：robot为所建机械臂模型；T′为要求反解的变换矩阵；q0为该机械臂的初始位置向量；M为机械臂的自由度标称向量，即当自由度为6时,M=[111111],若其中一个元素为0，则表示忽略该关节的自由度。结合该机械臂仿真模型，取初始位置向量q0=[0-pi/20000]，若机械臂末端点的坐标位置为Q2，则其变换矩阵为：

(20)

再调用函数qi=ikine(robot，T′，q0，M)，可得机械臂在Q2点的关节位置向量qi=[0 -1.570 80000]。

由上述正、逆运动学方程计算结果可知，所建仿真模型是正确的，可用于机械臂运动轨迹仿真。

3.3 机械臂运动轨迹仿真

在Robotics Toolbox中，可利用jtraj函数进行机械臂关节空间规划。调用jtraj函数的格式为：[qqdqdd]=jtraj(q0,q1,t)。这里，可将q视为状态q0到状态q1的关节空间规划轨迹，qd、qdd分别为该规划轨迹的速度和加速度，t为给定的时间长度向量。

针对正运动学方程和逆运动学方程，在轨迹规划后，分别利用fkine函数进行前向求解，可得到关节的位置、速度和加速度。定义该机械臂的起始位置为A点，终止位置为B点，可利用已建立的模型进行机械臂运动轨迹仿真。其程序如下：

t=0:0.056:2;时间范围，0.056为步长

q0=[0-pi/20000];初始位置

q1=[-pi/2-pi/2pi/3-pi/2pi/3pi/3];要到达的位置

[q,qd,qdd]=jtraj(q0,q1,t);轨迹规划

plot(r,q);画出机械臂运动图

T=fkine(r,q);计算变换矩阵

m=squeezeT(i,4,:);提取动态变换矩阵(i=1,2,3)

plot3(x,y,z);画出空间轨迹

plot(t,q(:,i));画出角位移随时间变化曲线(i=1，2，3，4，5，6)

plot(t,qd(:,i));画出角速度随时间变化曲线

plot(t,qdd(:,i));画出角加速度随时间变化曲线

通过轨迹规划，不仅可得到机械臂末端执行器的空间轨迹，而且还能得到各关节角位移、角速度和角加速度随时间的变化曲线。图6所示为机械臂的初始位置。图7所示为机械臂的终点位置。图8所示为机械臂末端的空间移动轨迹。从图8可看出，机械臂末端执行器达到了指定的位置，这证明机械臂运动模型的设计正确。图9所示为机械臂末端在空间各平面上的位置变化曲线。

图6 机械臂在起点的位置状态

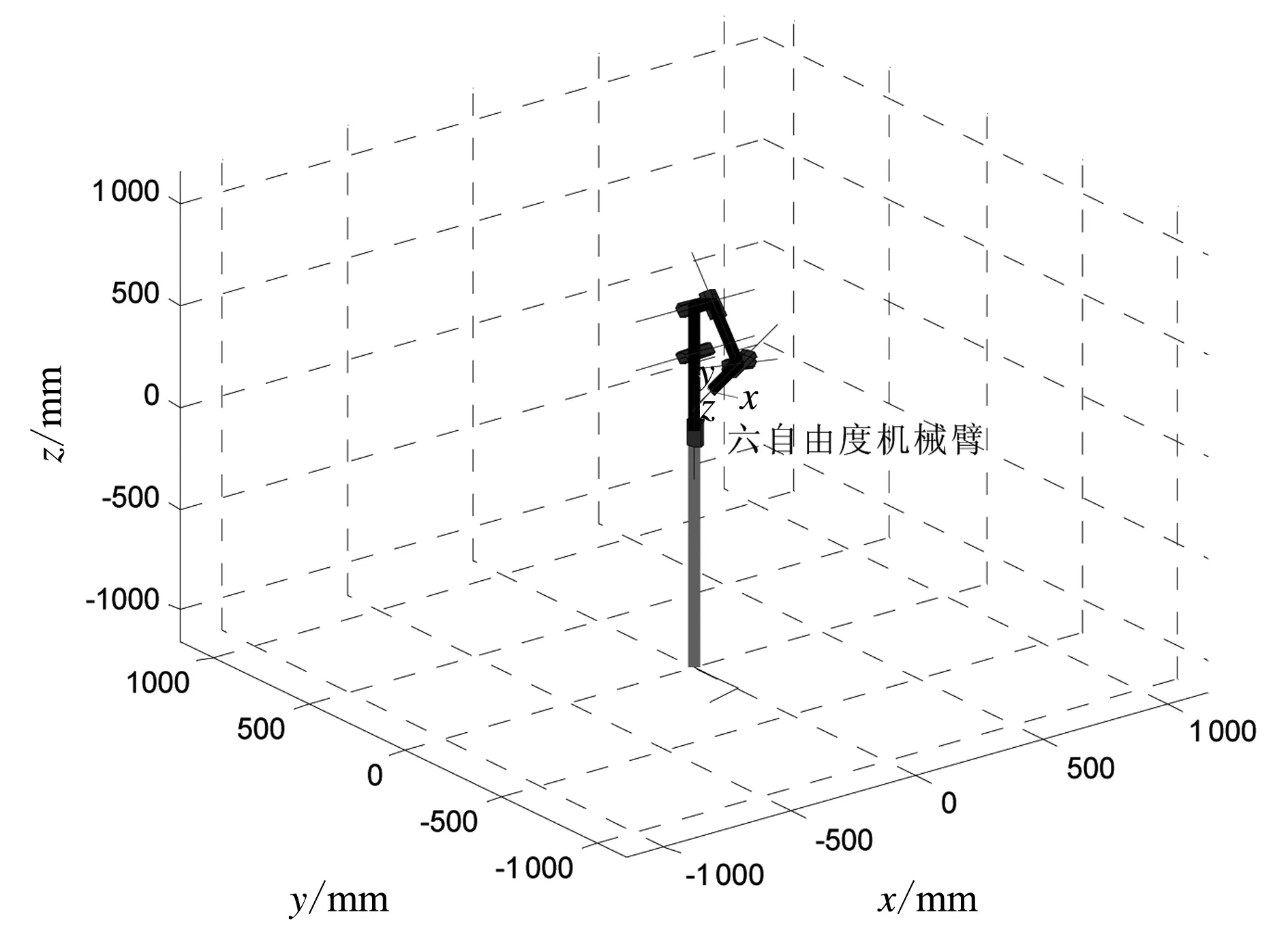
图7 机械臂到达终点的位置状态

关节1的角位移时间曲线、角速度时间曲线及角加速度时间曲线都是连续平稳的(见图10)。受篇幅所限，这里省略了关节2～6的角位移、角速度和角加速度时间变化曲线。综上所述，在理论上，该机械臂各关节和各运动部件的运行是平稳的。

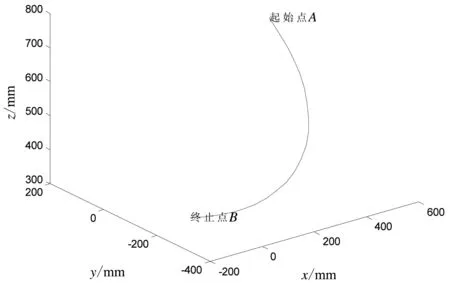
图8 机械臂末端的空间移动轨迹

图9 机械臂末端在空间各平面上的位置变化曲线

图10 关节1角位移、角速度和角加速度随时间的变化曲线

4 结 语

利用D-H参数法建立机械臂的空间坐标系，并且建立了机械臂运动学方程。运用蒙特卡罗法在Matlab软件中对机械臂的工作空间进行仿真分析，得到机械臂的空间工作范围，并验证了其可行性和正确性。利用Matlab中的Robotics Toolbox建立机械臂仿真模型，对机械臂的正、逆运动学方程进行了验证。通过运动轨迹规划仿真，得到了机械臂末端执行器的空间轨迹及各关节的角位移、角速度和角加速度随时间变化的曲线。本文能够为机械臂控制系统设计、动力学分析和轨迹规划提供借鉴。