基于分析驱动设计的封闭白车身轻量化多目标优化∗

吕天佟,王登峰,王传青

(1.吉林大学,汽车仿真与控制国家重点实验室,长春 130022； 2.北京汽车股份有限公司研究院,北京 101300)

前言

汽车质量每减轻100kg,每1L燃油可多行驶1km[1]。车身占汽车总质量的30%～40%,空载情况下,70%的燃油消耗在车身上[2]。目前主要的轻量化设计方法有结构、工艺和新材料等方面[3]。使用新材料往往伴随着新工艺的投入、模具的改变和成本的升高。因此结构轻量化是车身轻量化最常用的方法之一。

传统方法上白车身结构轻量化是以白车身质量、模态频率或刚度为目标,在约束白车身,其他性能不显著降低的前提下,寻找零部件形状、板件厚度等参数的最佳组合。传统方法没有考虑部件主断面的影响,而部件主截面决定了梁单元的实际性能,从而影响到车身性能和质量。另外部件形状、厚度参数的最佳组合大多是在近似模型的基础上得到的,优化过程中白车身结构不能根据性能的变化实时更新,不能实现“分析驱动设计”的开发理念。

本文中采用SFE-CONCEPT软件建立了隐式参数化封闭白车身模型,综合考虑零部件形状、板件厚度、主断面位置、主断面形状等参数,寻找各参数之间的最佳组合。本文建立的隐式参数化模型可以实现CAD模型改变与CAE模型前处理同步的功能,结合模块化处理可快速分析封闭白车身相应的性能。根据性能梯度的变化,结合优化算法的搜索功能,直接实现封闭白车身模型向着性能高、质量低的方向变化,实现“分析驱动设计”的理念。本文中以封闭白车身质量最低、静态扭转刚度最高为目标；约束封闭白车身的静态弯曲刚度,1阶弯曲模态频率性能不降低和弯曲、扭转工况下的最大应力不增加的情况下对封闭白车身进行轻量化多目标优化。

1 封闭白车身隐式参数化建模

参数化模型包括显式参数化和隐式参数化模型。显式参数化模型在网格变化的基础上实现模型改变,虽然部分建模软件提供了“Re-mesh”功能,但在模型变动较大的情况下,网格质量仍然较差[4]。SFE-CONCEPT软件建立的隐式参数化模型,首先建立一系列的基点(Influence point)、基线(Base line)来实现模型部件定位；其次建立相应的局部截面并分配到基线上创建梁(beam),曲率大的部件通过在大曲率处定义接头(joint)实现梁与梁的连接；然后通过映射(mapping)功能将不同的梁连接成一体,并对梁赋予材料属性；最后通过网格划分功能生成有限元模型并进行相应的性能分析。为提高建模效率,本文中忽视了过线孔、减重孔等特征,建立的隐式参数化封闭白车身如图1所示。

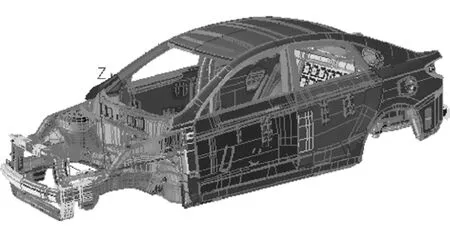
图1 隐式参数化封闭白车身模型

2 封闭白车身性能分析

参数化封闭白车身在创建过程中忽视了部分特征,可能影响随后生成的有限元模型性能。为验证封闭白车身模型的性能是否满足轻量化优化要求,本文中对封闭白车身的仿真性能与试验进行对比。

2.1 封闭白车身静态弯扭刚度分析

封闭白车身静态弯扭刚度性能试验时,用带力传感器高度可调的支架约束封闭白车身前悬架减振塔,用固定刚性支架全约束后悬架弹簧安装支座,如图2所示。

图2 封闭白车身静态弯扭刚度的约束

弯曲刚度试验时,将加载砝码放置在车身地板上B柱附近,最大载荷为4 000N；扭转刚度试验时,用前约束加载装置中的丝杠对车身施加2 000N·m的扭矩载荷。采用百分表测量封闭白车身的变形量,得出最小静态弯扭刚度。封闭白车身静态弯扭刚度仿真分析时采用与试验相同的设置。表1为封闭白车身静态弯扭刚度仿真分析和试验结果对比。从表1可知,仿真和试验结果相比,静态弯曲和扭转刚度相对误差分别为6.7%和3.3%。

2.2 封闭白车身低阶模态分析

系统封闭白车身振动方程为

表1 封闭白车身静态弯扭刚度仿真和试验对比

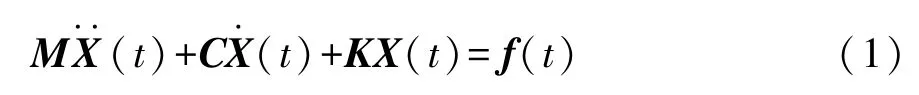
式中:M,C,K分别为系统质量、阻尼、刚度矩阵；X(t),t)为系统节点的位移、速度、加速度矩阵；f(t)为N维数系统激振力矩阵。经傅里叶变换并整理得测量点i和激振点p的频响函数为

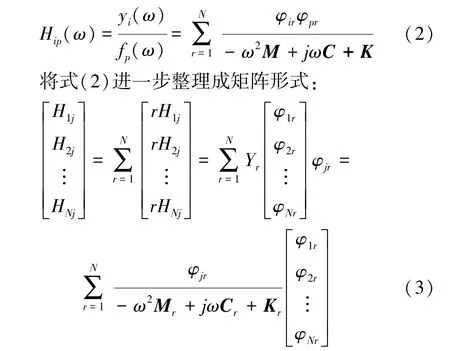
从式(3)中可知,在某点施加激振,拾取所有的激励,可得出所有的模态参数。白车身是一个大型系统,在左前、右后对其施加了2个激振力,前激励力垂直向上、后激励力与侧向和纵向倾斜一定角度。封闭白车身模态试验时,将被试封闭白车身水平支撑在4个空气弹簧上,如图3所示。

图3 封闭白车身模态试验支撑

信号发生器发出0～256Hz的触发随机信号,经功率放大器放大后通过激振器施加到车身上。用3向加速度传感器拾取封闭白车身上各测点的振动加速度响应,整个封闭白车身共布置180个测点。

封闭白车身低阶模态频率仿真和试验对比如表2所示,除前部扭转模态频率误差为7.00%外,其他模态频率误差均小于1.70%。

表2 白车身低阶模态频率仿真和试验对比

2.3 封闭白车身弯扭工况强度分析

汽车在行驶过程中会受到各方向的载荷,其中弯曲和扭转载荷是最常见的工况。根据GB/T 5910—1998的要求,将 5名乘员(5×68kg)、行李(7kg)、燃油(37.7kg)和发动机(182kg)等有效载荷通过mass点加载到相应的位置上。作用在车身上的垂向力为

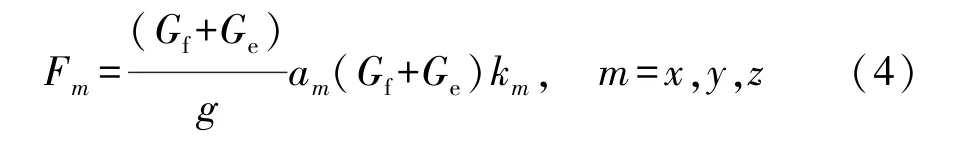
式中:Gf为悬架支撑的车身系统的自身载荷；Ge为车身有效载荷；km为动荷系数。km计算方法比较复杂,最常用的表达式为

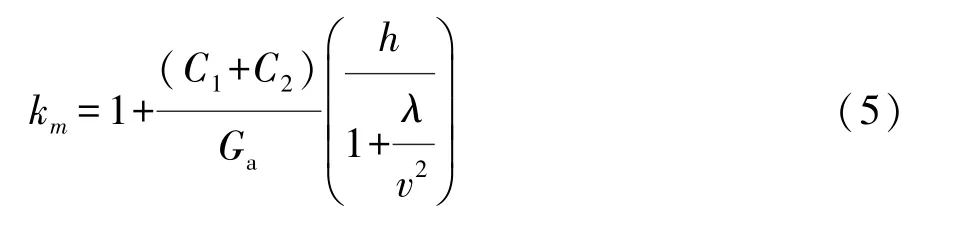
式中:C1,C2分别为前、后悬架与轮胎的合成刚度；Ga为汽车总重力；h为路障高度；λ为经验系数；v为车速。乘用轿车的动荷系数通常为1.75[5]。对封闭车身施加17.15m/s2的加速度并约束前端减振塔、后端弹簧安装支座,左前减振塔和右后弹簧安装支座的全部自由度,分别进行弯曲、扭转工况下的强度分析。封闭车身各部件在弯曲、扭转工况下的仿真最大应力均小于许用应力。仿真和试验最大Mises应力均发生在右侧后悬支撑板上,对比如表3所示。

表3 仿真和试验最大Mises应力对比

由于加载和约束接触面积的影响,封闭白车身最大应力的试验值小于仿真值。其弯曲和扭转工况的相对误差分别为7.52%和3.23%。因此封闭参数化模型的静态弯扭刚度,1阶弯曲模态频率、弯曲和扭转强度仿真精度满足要求,可进行轻量化优化。

3 封闭白车身设计变量

隐式参数化模型可通过改变基点、特征位置和主断面形状实现封闭白车身结构的变化。主断面结构对白车身的模态频率、刚度和强度有重要的影响,然而轻量化优化过程中鲜有考虑主断面形状、特征位置的影响。因此本文中在考虑部件形状、厚度、局部截面位置等变量基础上增加了主断面变量。

本文中以Shotgun的主断面为例来详细说明,Shotgun主断面通过Node和Segment定义,并随之将其参数化。通过调整Node的位置参数和Segment的曲率参数实现主断面形状的改变,如图4所示。主断面变化后部件结构有较大的变化,其性能也随之而变。通过协同调整一系列的Node位置参数和Segment曲率参数实现主断面缩放和形状的改变,再结合基点参数实现主断面位置的改变。通过确定合理的参数值变化范围,实现轻量化优化中封闭白车身在设计空间内生成多种主断面。另外通过基线曲率、主断面形状和位置变量的组合实现车身结构部件形状与曲率的变化。

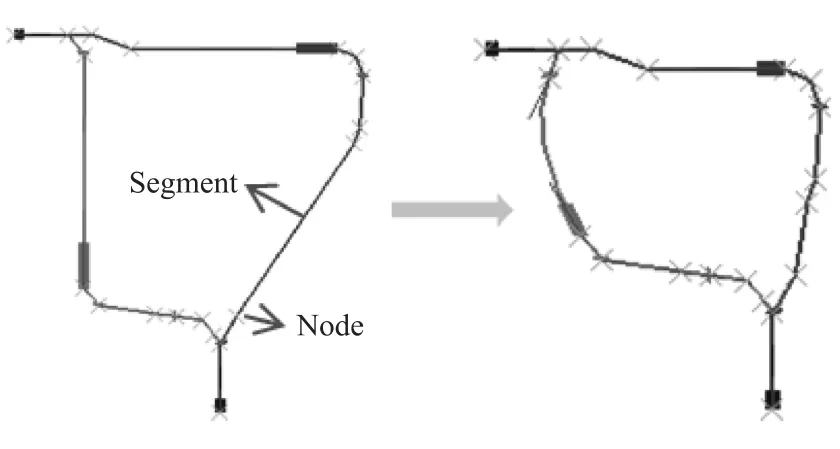
图4 Shotgun主断面形状变化

图5 设计变量所在的部件

因本文中没有考虑碰撞等安全性能,因此选取的设计变量不包含对安全性能影响较大的部件。轻量化优化中选取54个白车身设计变量,如图5所示。其中厚度变量42个,主断面形状变量10个,主断面位置变量2个,如图6所示。经过后续的优化可实现主断面形状、板件厚度、部件曲率的最佳组合,充分发挥结构承载、加强和轻量化的作用。

图6 主断面变量所在的部件

4 封闭白车身轻量化优化

本文中通过参数值实现封闭白车身参数化模型的改变,再结合网格划分功能快速实现封闭白车身有限元模型的变化与更新。将封闭白车身有限元模型设置成封闭白车身模块,并将弯扭刚度、低阶模态和弯扭强度工况性能分析所需的关键字分别设置成独立的头文件模块。各头文件模块结合封闭白车身模块可快速实现相应的性能分析,模块化过程如图7所示。

图7 白车身模块化过程

通过改变参数值实现封闭白车身结构变化,结合模块化设置实现封闭白车身结构优化的后台全自动运算。结构优化方法分为近似模型优化和直接优化两类[6]。近似模型方法用于解决单次仿真时间过长的问题,计算效率高但计算结果精度低；直接优化方法计算结果精度高但计算效率低。由于封闭白车身刚度、模态及强度仿真计算效率高,因此本文中采用精度较高的直接优化方法。封闭白车身后台全自动优化流程如图8所示。图8中“optimization”为优化模块,采用NSGA-II算法(第二代非劣排序遗传),该算法具有计算复杂度低、收敛速度快的特点。“parametric model”为参数化封闭白车身模块,“mo-dal”为封闭白车身模态计算模块,“stiffness”为封闭白车身弯扭刚度计算模块,“nastran”为封闭白车身弯扭强度计算模块。

图8 封闭白车身后台全自动优化流程

NSGA-II算法以初始种群为依据,采用快速非支配排序方法、精英保持策略和拥挤度比较方法收敛到优化解集[7]。结合参数化模型、全自动优化流程和NSGA-II算法的搜索功能实现“分析驱动设计”的优化理念,使封闭白车身模型向着性能高、质量低的方向迭代。根据以上分析,封闭白车身优化的物理模型为

式中:Mmin(x)和ktmax(x)分别为封闭白车身的最小质量和最大静态扭转刚度；fbo和kbo分别为优化模型的1阶弯曲模态频率和静态弯曲刚度；Sbo和Sto分别为弯曲强度,扭转强度；fbi和kbi分别为初始模型的1阶弯曲模态频率和静态弯曲刚度；Sbi和Sti分别为弯曲强度和扭转强度；x为封闭白车身设计变量。

5 封闭白车身优化前后性能对比

使用NSGA-II算法优化搜索到妥协解集,本文中选取封闭白车身质量最小的妥协解作为轻量化优化解,并对轻量化前后的白车身质量和性能进行对比。轻量化前封闭白车身的质量为424.77kg,轻量化后质量为392.36kg,减质量32.41kg,轻量化率达7.63%。

表4为轻量化优化前后封闭白车身静态弯扭刚度对比。轻量化优化后封闭白车身弯曲刚度降低119.18N/mm,变化率为0.74%；轻量化优化后封闭白车身扭转刚度增加199.51N·m·(°)-1,变化率为1.09%。

图9为轻量化优化前后1阶弯曲模态对比,从图9中可知轻量化前的封闭白车身1阶弯曲模态频率为51.54Hz,轻量化后的1阶弯曲模态频率52.02Hz,频率提高0.48Hz,变化率为0.93%。

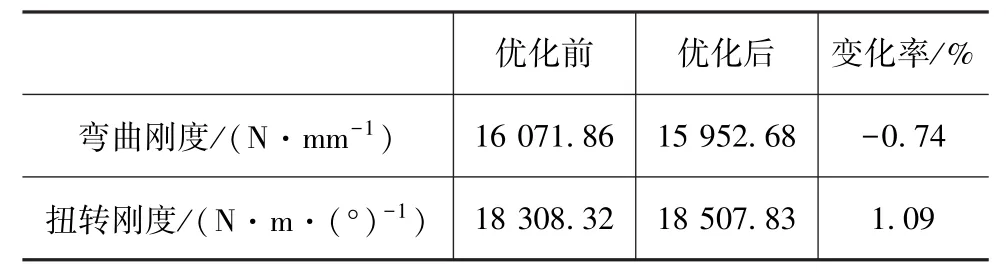
表4 轻量化前后封闭白车身静态弯扭刚度对比

图9 封闭白车身轻量化优化前后1阶弯曲模态对比

图10和图11分别为弯曲工况下封闭白车身轻量化优化前后的强度云图。轻量化优化前封闭白车身的最大应力为256.9MPa,轻量化优化后最大应力为250.0MPa。轻量化优化前后最大应力都发生在封闭白车身的后悬架支撑板上。轻量化优化后的最大应力减小6.9MPa,减幅达2.69%。

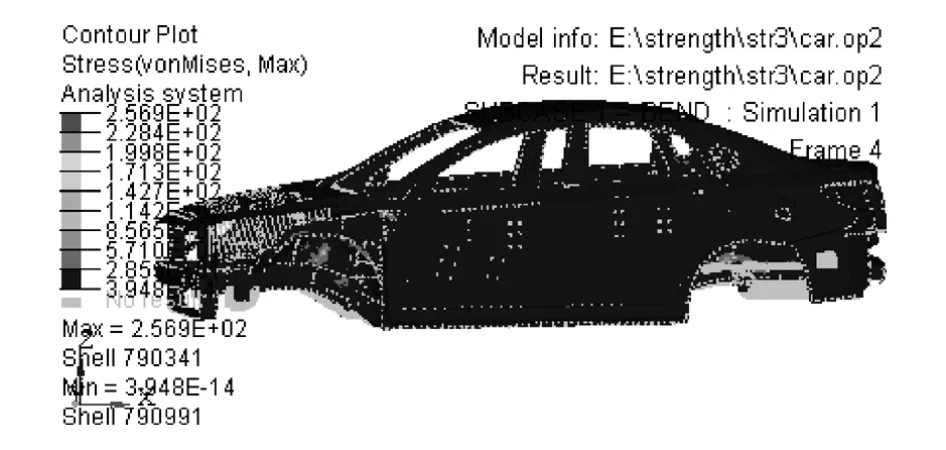
图10 封闭白车身轻量化优化前弯曲工况的强度

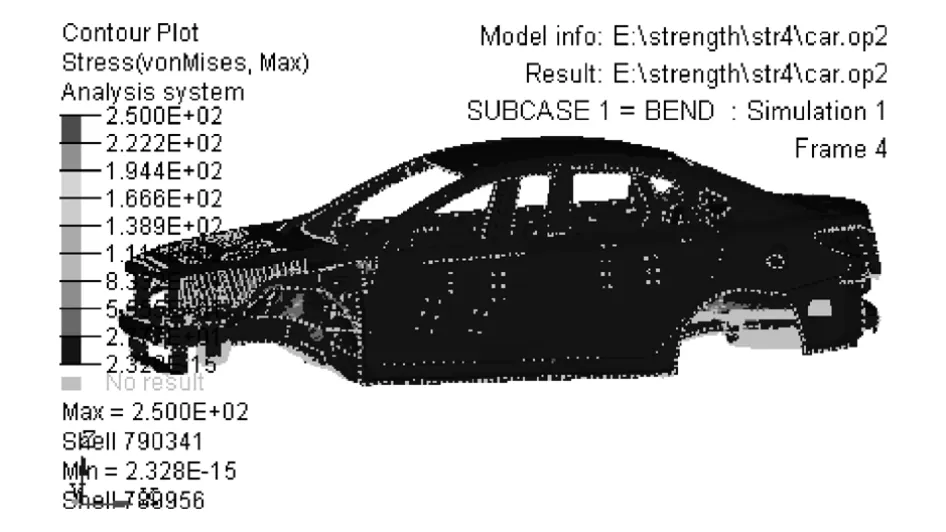
图11 封闭白车身轻量化优化后弯曲工况的强度

图12和图13分别为扭转工况下封闭白车身轻量化优化前后的强度云图。轻量化优化前封闭白车身的最大应力为546.7MPa,轻量化优化后最大应力为540.8MPa。轻量化优化前后最大应力都发生在封闭白车身的后悬架支撑板上。轻量化优化后的最大应力减小5.9MPa,减幅达1.08%。

图12 封闭白车身轻量化优化前扭转工况的强度

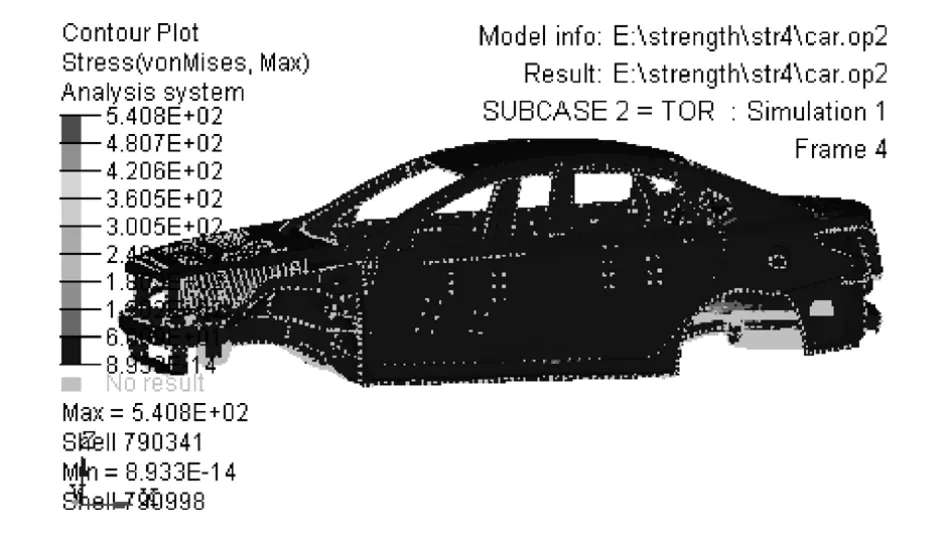
图13 封闭白车身轻量化优化后扭转工况的强度

6 结论

通过参数化封闭白车身提取板件厚度、主断面位置、主断面形状等变量,实现了将合适的结构、合适的厚度用在合适的位置。进一步对封闭白车身进行模块化设置,实现了有限元模型变动、更新和分析的后台全自动运算。结合NSGA-II优化算法的搜索功能,实现了“分析驱动设计”的理念。另外,经过轻量化优化封闭白车身的质量降低32.41kg,轻量化率达7.63%。轻量化优化后封闭白车身静态弯曲刚度降低,变化率为0.74%；封闭白车身的静态扭转刚度提升,变化率为1.09%,1阶弯曲模态提升,变化率为0.93%,弯曲、扭转工况下白车身最大应力降低,变化率分别为2.69%,1.08%。