Ti6Al4V钛合金扭转复合微动特性研究

张媛媛，王宇星，刘 娟，沈火明

(西南交通大学 力学与工程学院， 成都 610031)

微动是2个接触界面之间发生小位移幅值的相对运动[1]。在实际工程中微动行为非常复杂，通常是多种基本微动模式的复合。扭转复合微动主要存在于具有扭动微动和旋转微动运动的球窝接触的界面中[2]。钛合金具有低密度、高延展性以及抗腐蚀等优良特性，已广泛应用于航空航天、船舶制造业、化工以及人工关节中[3-6]。人工关节的球窝式连接能完成扭动、转动以及二者复合的相对运动，从而满足不同的功能需求。人造牙齿中的钛合金为球窝式连接，在口腔中会承受具有腐蚀性的微动[7]。

由于微动会产生局部裂纹的萌生和扩展，已成为一些零部件失效的关键因素之一，因此，很多学者对扭转复合微动进行了研究。Briscoe等研究了在刚性球作用下的PMMA聚合物的扭转复合微动行为，给出了不同倾斜角度对微动损伤的影响[8]。沈明学等[9-11]已形成了一套完整的试验体系，从机理上对扭转复合微动进行了分析。在有限元模拟中，主要集中于对扭动微动[12-13]、转动微动的研究[14]，而对扭转复合微动特性[15]的报道较少。周琰等[9]对Ti6Al4V钛合金进行了扭转复合微动特性的试验研究，相关数值模拟还未见报道。

基于ABAQUS软件，采用球/平面摩擦副，建立了Ti6Al4V钛合金试样在52100钢球作用下的扭转复合法微动的三维有限元模型，研究不同倾斜角和角位移幅值对扭转复合微动行为的影响。

1 有限元模型的建立

根据圣维南原理，将实心球压头简化为空心半球[10]，并将半球和试样在接触区附近的块体分别单独建立，以便对研究区域进行网格细划，如图1(b)和1(c)所示。将空心半球上表面刚性耦合到球心处的参考点，将力和位移荷载均施加在该点上。扭转复合微动是由球形压头的实际旋转轴与接触面法向之间的角度偏差形成的，将该偏差角α称之为倾斜角，θ为角位移幅值。当α为0是纯扭动微动，当α为π/2是纯转动微动，如图1(a)所示。

已知空心半球的半径为20 mm，试样块体半径为5 mm、厚度为4 mm。为减小计算量，可设试样和压头接触区块体半宽均为1 mm。

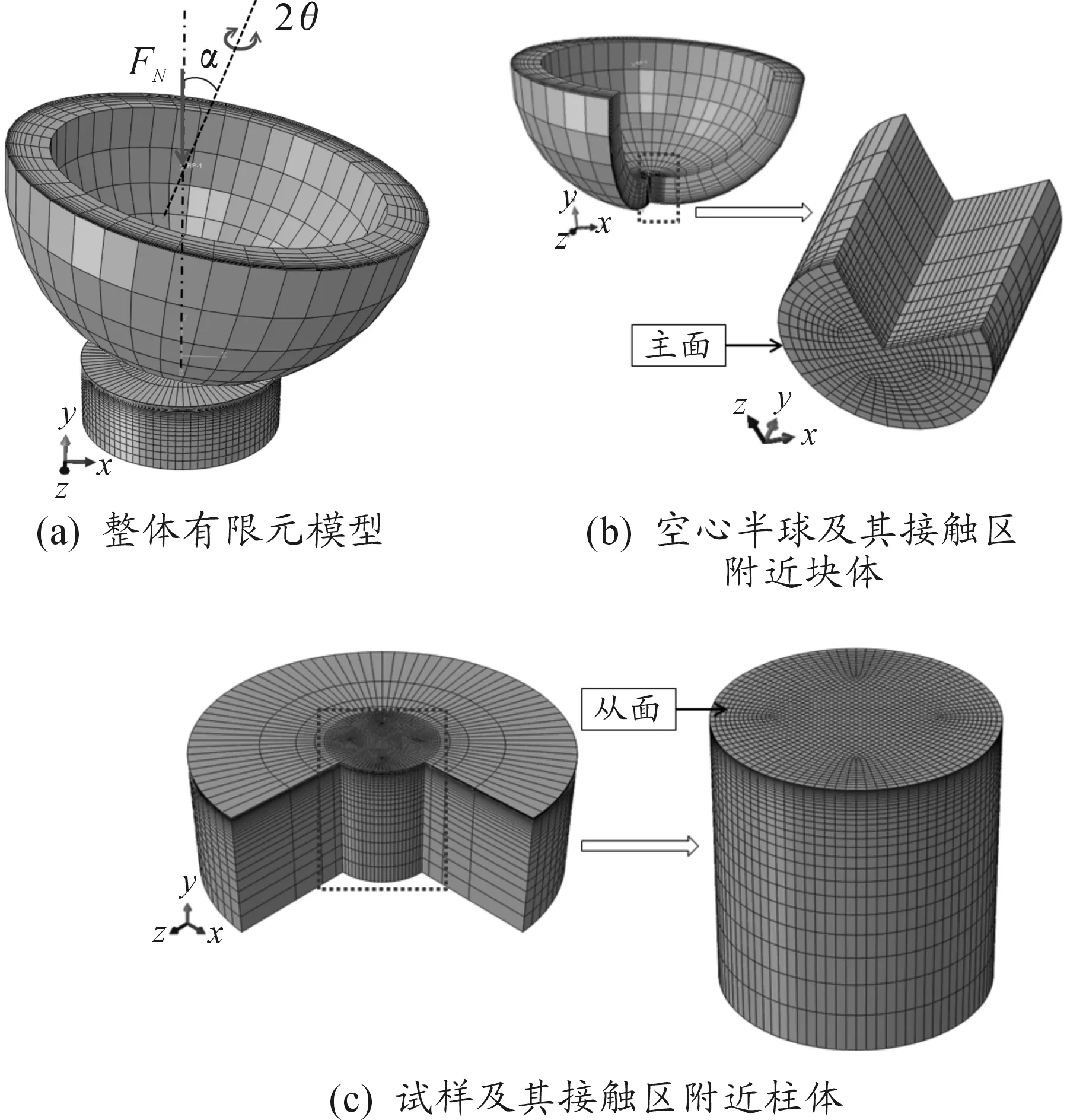
图1 有限元模型

网格数量信息如表1所示，最小单元尺寸为14.8 μm×14.8 μm×30.0 μm。虽然接触区域块体尺寸远小于整体模型，但其单元数占总单元数94.57%，单元密度远远大于远离接触区处。因此，采用本文建模方法便于对网格进行细化，也可进一步提高计算精度和效率。

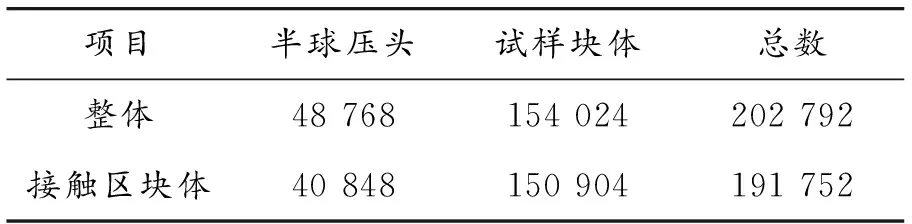
表1 有限元模型单元数量

计算过程由4个分析步构成，即系统默认的初始分析步，并新设第2、第3和第4分析步。

1) 设置边界条件：在初始分析步中，将试样底部表面设为全约束，使试样既不会产生刚体位移，又不影响其变形。

2) 完成法向荷载作用：首先，在参考点上施加向下的法向荷载；其次，在参考点上施加位移条件，设其仅沿y方向自由移动，其他5个自由度均设为0。

3) 完成扭动微动：修改由第2分析步传递的位移条件，将y方向的角位移由0改为角位移幅值θ的扭动分量(θ)y，即θ×cosα；其他值保持不变。

4) 完成扭转复合微动：修改由第3分析步传递的位移条件，将x方向的角位移由0改为角位移幅值θ的转动分量(θ)x，即θ×sinα；其他值保持不变。

2 模型正确性验证

球形压头与试样块体的材料力学性能如表2所示。摩擦因数为0.43，本构关系如文献[16]所示。当法向荷载为50 N时，接触半径和最大压力的Hertz理论解[17]和数值解如表3所示。坐标原点为接触中心，接触压力沿任意直径上的分布如图2所示。

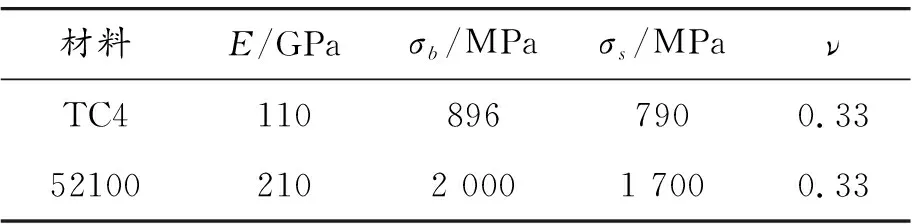
表2 材料的主要力学性能

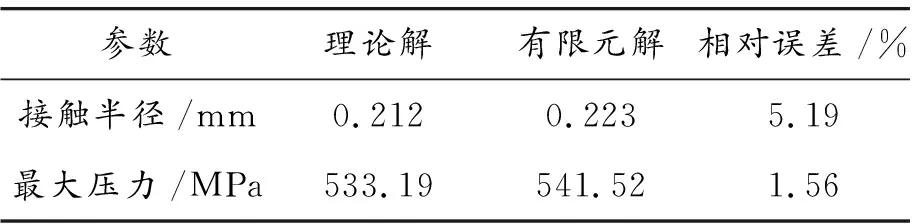
表3 Hertz理论和数值方法结果对比

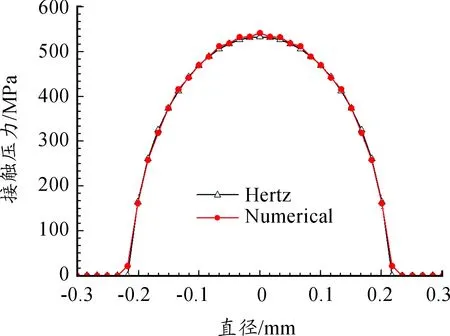
图2 接触表面压力分布

对比分析可知，有限元解和Hertz理论分析结果能够较好地吻合，验证了本文所建模型的正确性。接触半径和最大压力的数值解略大于理论解，这可能是在有限元建模时采用了简化模型，降低了系统刚度所致。

3 扭转复合微动研究

3.1 倾斜角对应力分布的影响

为了研究在部分滑移区、混合区和滑移区，角位移幅值θ和倾斜角α对接触压力和Mises应力分布的影响，本文计算工况参考文献[9]。

当法向荷载FN为50 N、角位移幅值θ为0.5°且倾斜角α分别为10°、20°、40°和60°时，研究了接触压力和Mises应力分布随α的变化规律。α为10°时,微动运行于部分滑移区，其他均属于混合区，循环次数为3.5周。

首先定义接触表面过坐标原点的路径，如图3(a)所示。压力分布如图3(b)所示。Mises等效应力分布规律如图4所示(以θ为0.5°，α为0°、20°、60 °和90°为例)。

图3 接触压力随倾斜角的分布(FN=50 N，θ=0.5°)

由图3(b)可知，当θ为0.5°、α为0°时，接触压力分布与仅受法向荷载作用下基本一致，说明扭动微动对压力分布几乎没有影响。随着倾斜角的增加，接触半径和压力的大小基本没有变化，但整体向左偏移，即接触中心偏移方位与转动方向一致，这是由于转动分量作用的结果。

由图4(a)和(d)可知：当倾斜角α=0°时(纯扭动微动)，Mises应力云图在横向和纵向均为“环状”对称分布，在距接触中心相同半径处，应力值相同，最大应力位置并不在接触中心，而是出现在离接触中心稍远处的周围区域；当倾斜角α=90°时(纯转动微动)，Mises等效应力云图呈放射性分布，且方向与半球模型转动方向一致。

由图4(b)和(c)可知：当α大于10°小于90°时(扭转复合微动)，无论在接触表面还是沿厚度方向，应力云图呈现出不对称性。在接触面上，应力云图向z的正方向(转动方向)偏移；而在纵向，朝着z的负方向(与转动相反方向)偏移。应力值与半径、周向和纵向位置相关，且大于相应的纯扭动微动。因此，Mises应力分布的不对称性主要是由转动分量引起。说明倾斜角对改变扭转复合微动有重要影响。

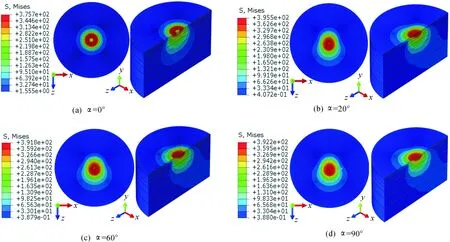
图4 Mises等效应力云图随倾斜角的分布(FN=50 N，θ=0.5°)

3.2 角位移幅值对应力分布的影响

当法向荷载FN为50 N，倾斜角α为20°且角位移幅值θ分别为0.25°、0.5°、1°、2°和5°时，其接触压力分布如图5所示，Mises等效应力分布云图如图7所示(以θ为2°和5°为例)。其中，θ为0.25°时微动运行于部分滑移区；θ为0.5°和1°时微动运行于部分滑移区；其他属于滑移区。

由图5可知，当倾斜角α为20°时，接触压力随着角位移幅值的增加而增大，且其分布偏移方向与转动方向一致。这可能是转动分量值增加的缘故。因此，在纯扭动微动中，角位移幅值的增加基本不影响接触压力的分布[12]，而在纯转动微动中接触压力增加[14]。因此，无论微动运行于部分滑移区、混合区还是滑移区[9]，接触半径和接触压力主要由法向荷载控制。

图5 不同角位移幅值下的接触压力分布(FN=50 N，α=20°)

由图6以及图4(b)可知，不同的角位移幅值下，Mises等效应力云图形状相似，均为不对称分布。当2θ小于2°时，幅值的改变对应力分布影响较小；当2θ为5°时，应力值明显增加。

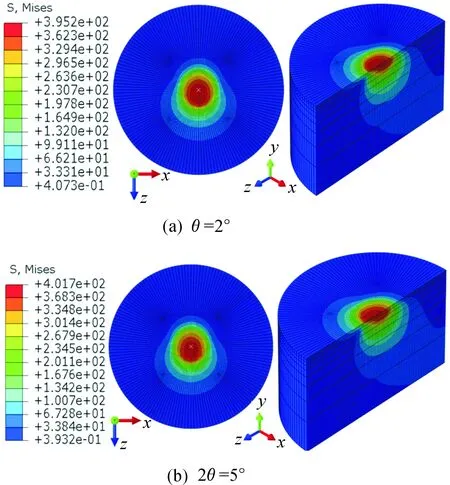
图6 Mises应力在表面和沿厚度方向分布云图(FN=50 N，α=20°)

4 结论

1) 所建立的扭转复合微动有限模型，能够快速准确地对3种类型的微动进行模拟计算，即纯扭转微动(α=0°)、纯转动微动(α=90°)以及扭转复合微动(0°<α<90°。)。

2) 随着倾斜角或角位移幅值的增加，接触压力也随之略有增大；Mises等效应力在横向和纵向均呈现出的不对称性均由转动分量引起；而接触半径和接触压力主要由法向荷载控制。

3) 当角位移幅值一定时，随着倾斜角的增加，扭转复合微动由扭动微动控制逐渐变为由转动微动控制，Mises等效应力也随之增大；当倾斜角一定时，角位移幅值成为影响扭转复合微动磨损行为的重要因素。Mises应力分布均随着角位移的变化而改变。因此，扭转复合微动控制非常依赖于倾斜角和角位移幅值。